课题学习 镶嵌
图片预览






文档简介
课件47张PPT。小 结 S h u x u e台州市书生中学朱仁江制作美妙的镶嵌2010-04-13埃舍尔(M.C.ESCHER1898-1972)荷兰现代版画艺术家。
他是一个将艺术与数学融合的画家,也因此享誉世界。
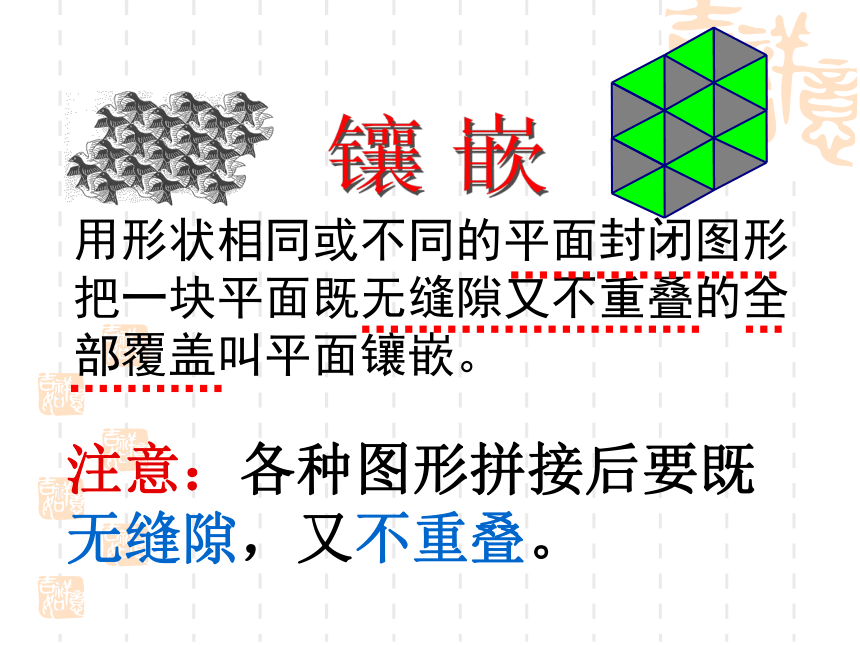
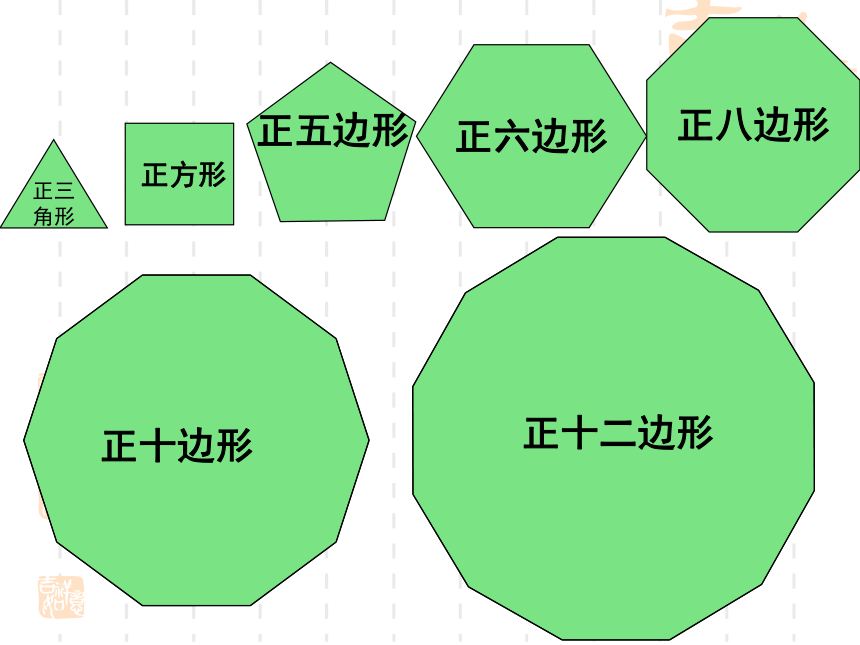
???资 料埃舍尔的作品欣 赏镶嵌用形状相同或不同的平面封闭图形把一块平面既无缝隙又不重叠的全部覆盖叫平面镶嵌。注意:各种图形拼接后要既无缝隙,又不重叠。1 关注数学中的美 2 关注身边的数学随堂启迪请你帮忙:小新搬新家了,他的房间要自己设计,地板想用一种正多边形的瓷砖来镶嵌,商店有以下几种瓷砖出售,请帮小新选一种。
正六边形正八边形正十边形正十二边形正五边形正方形正三
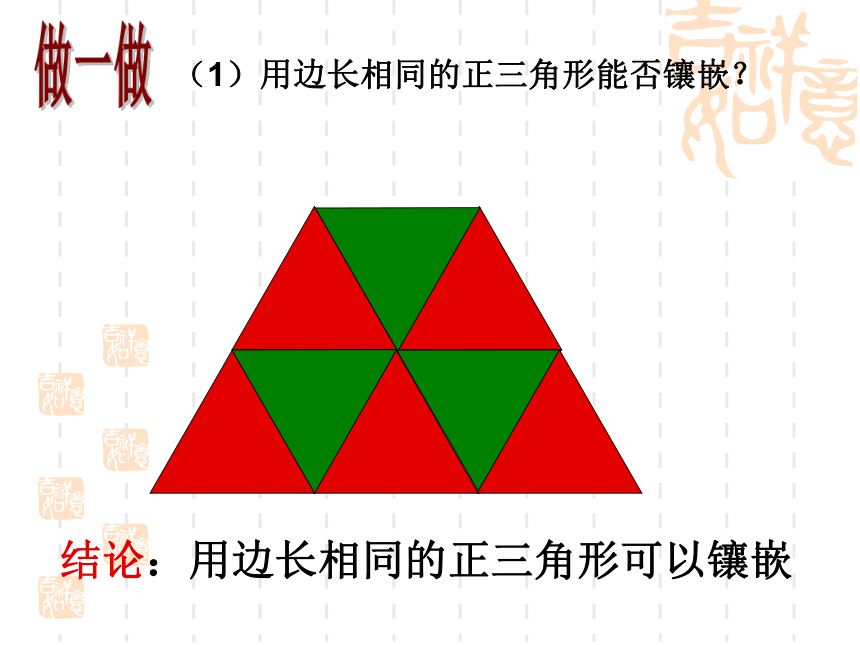
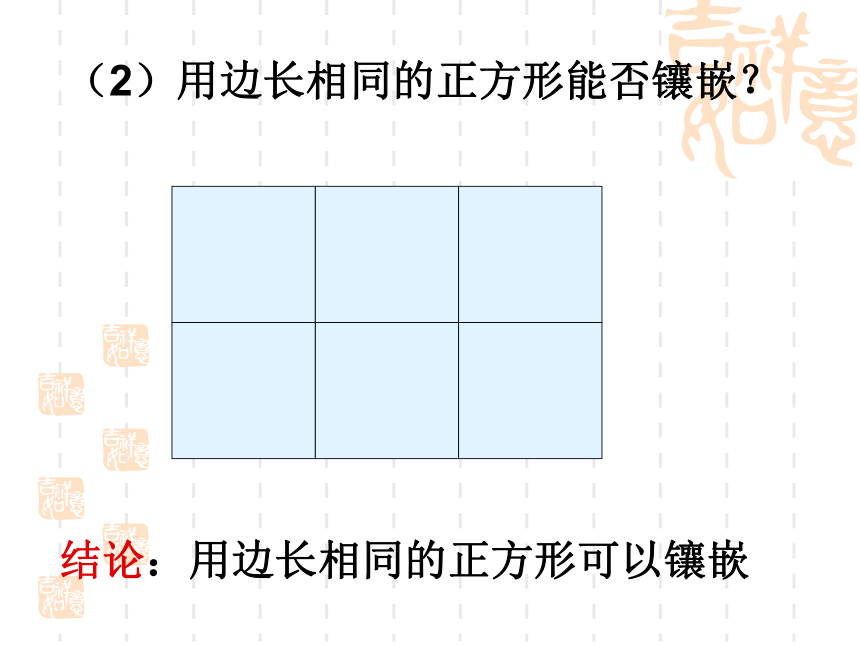
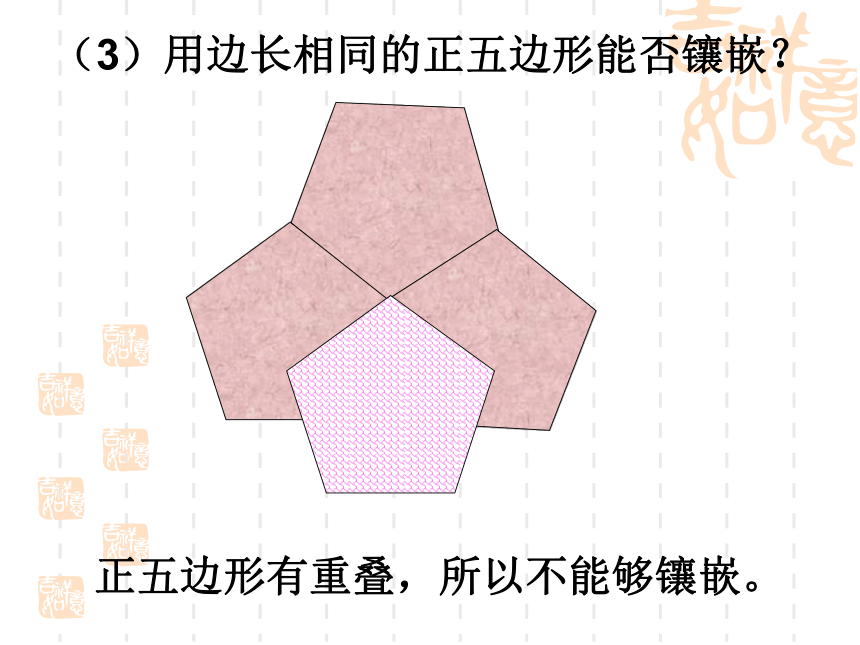
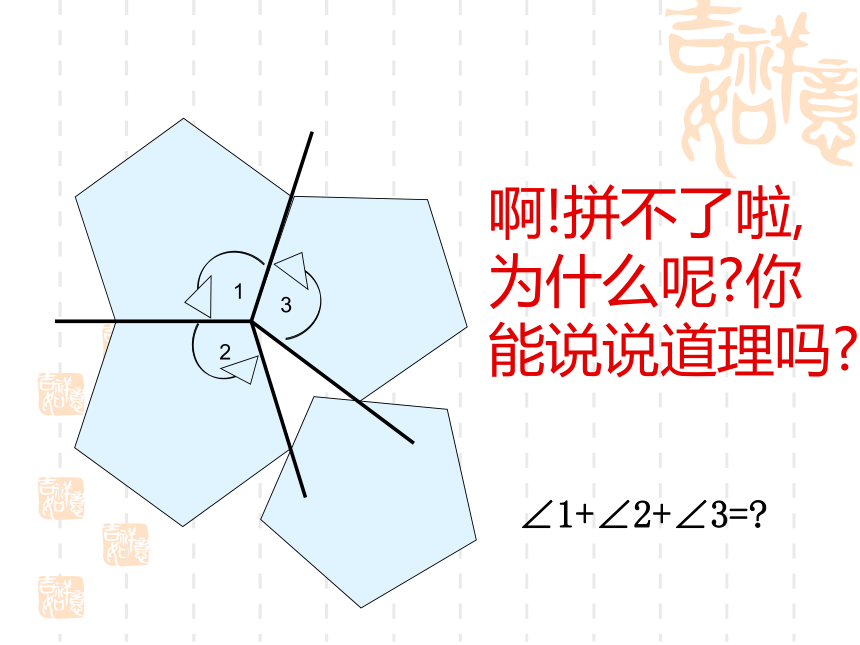
角形做一做 (1)用边长相同的正三角形能否镶嵌?结论:用边长相同的正三角形可以镶嵌(2)用边长相同的正方形能否镶嵌?结论:用边长相同的正方形可以镶嵌正五边形有重叠,所以不能够镶嵌。(3)用边长相同的正五边形能否镶嵌?啊!拼不了啦,为什么呢?你能说说道理吗?123∠1+∠2+∠3=?(4)用边长相同的正六边形能否镶嵌?结论:用边长相同的正六边形可以镶嵌八边形有重叠,所以不能够镶嵌。结论要用几个形状、大小完全相同的图形不留空隙、不重叠地镶嵌一个平面,需使得拼接点处的各角之和360°.正六边形正八边形正十边形正十二边形正五边形“内角必须整除360度” 要用正多边形镶嵌成一个平面的关键是 看:这种正多边形的一个内角的倍数是否是360°,在正多边形里,正三角形的每个内角都是60°,正四边形的每个内角都是90°,正六边形的每个内角都是120°,这三种多边形的一个内角的倍数都是360°,而其他的正多边形的每个内角的倍数都不是360°,所以说:在正多边形里只有正三角形、正四边形、正六边形可以密铺,而其他的正多边形不可密铺. 还能找到能密铺的其他正多边形吗?思考仅用一种正多边形镶嵌,
只有正三角形、正方形、正六边形
能镶嵌成一个平面。结论:思考:如果是任意的多边形,又有哪些能镶嵌呢?只有三角形和四边形。 同一种任意三角形、四边形可否镶
嵌成一个平面?问题用同一种平面图形如果不能密铺,用两种或者两种以上平面图形能不能密铺呢?做一做下列不同正多边形能否镶嵌?
正三角形与正方形?
正三角形与正五边形?
正三角形与正六边形?
正四边形与正六边形?
正三角形与正十二边形?正三角形与正方形∴2m+3n=12m=3
n=2设在一个顶点周围有 m个正三角
形的角,n个正方形的角,则有
∵ m,n 为正整数∴解为1)正三角形与正方形镶嵌图案设计2)正三角形与正六边形镶嵌图案设计∴m+2 n=6m=2
n=2m=4
n=1设在一个顶点周围有 m 个正三角形的角,
n 个正六边形的角,则有∵ m,n 为正整数∴解为4)正四边形
与正八边形5)正三角形与
正十二边形3)正五边形
与正十边形图案设计设在一个顶点周围有 m 个正五边形的角,n 个正十边形的角,则有∴3m+4n=10m=2
n=1∵ m,n 为正整数∴解为∴2m+3n=8m=1
n=2设在一个顶点周围有个 m 正四边形的角,
n 个正八边形的角,则有∵ m,n 为正整数∴解为用三种正多边形镶嵌,哪些能镶嵌成一个平面?探究问题(三)1、正六边形、正方形和正三角形的组合。2、正十二边形、正六边形和正方形的组合。 归纳三种不同正多边形进行镶嵌:
正三角形、正方形与正六边形,
正方形、正六边形与正十二边形。正三角形、正方形与正六边形正方形、正六边形与正十二边形
这节课你有哪些收获? 当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个平面图形。正三角形与正方形正三角形正方形正六边形正三角形与正六边形正三角形与正十二边形正三角形、正方形与正六边形正方形、正六边形
与正十二边形正五边形与正十边形
正四边形与正八边形
1、下列多边形一定不能进行平面镶嵌的是( )
A.三角形 B.正方形 C.任意四边形 D.正八边形 2、用正方形一种图形进行平面镶嵌时,在它的一个顶点周围的正方形的个数是( ) A.3 B.4 C.5 D.6 3、如果只用一种正多边形作平面镶嵌,而且在每一个正多边形的每一个顶点周围都有6个正多边形,则该正多边形的边数为( ) A.3 B.4 C.5 D.6DBA练习观察思考镶嵌图案欣赏
他是一个将艺术与数学融合的画家,也因此享誉世界。
???资 料埃舍尔的作品欣 赏镶嵌用形状相同或不同的平面封闭图形把一块平面既无缝隙又不重叠的全部覆盖叫平面镶嵌。注意:各种图形拼接后要既无缝隙,又不重叠。1 关注数学中的美 2 关注身边的数学随堂启迪请你帮忙:小新搬新家了,他的房间要自己设计,地板想用一种正多边形的瓷砖来镶嵌,商店有以下几种瓷砖出售,请帮小新选一种。
正六边形正八边形正十边形正十二边形正五边形正方形正三
角形做一做 (1)用边长相同的正三角形能否镶嵌?结论:用边长相同的正三角形可以镶嵌(2)用边长相同的正方形能否镶嵌?结论:用边长相同的正方形可以镶嵌正五边形有重叠,所以不能够镶嵌。(3)用边长相同的正五边形能否镶嵌?啊!拼不了啦,为什么呢?你能说说道理吗?123∠1+∠2+∠3=?(4)用边长相同的正六边形能否镶嵌?结论:用边长相同的正六边形可以镶嵌八边形有重叠,所以不能够镶嵌。结论要用几个形状、大小完全相同的图形不留空隙、不重叠地镶嵌一个平面,需使得拼接点处的各角之和360°.正六边形正八边形正十边形正十二边形正五边形“内角必须整除360度” 要用正多边形镶嵌成一个平面的关键是 看:这种正多边形的一个内角的倍数是否是360°,在正多边形里,正三角形的每个内角都是60°,正四边形的每个内角都是90°,正六边形的每个内角都是120°,这三种多边形的一个内角的倍数都是360°,而其他的正多边形的每个内角的倍数都不是360°,所以说:在正多边形里只有正三角形、正四边形、正六边形可以密铺,而其他的正多边形不可密铺. 还能找到能密铺的其他正多边形吗?思考仅用一种正多边形镶嵌,
只有正三角形、正方形、正六边形
能镶嵌成一个平面。结论:思考:如果是任意的多边形,又有哪些能镶嵌呢?只有三角形和四边形。 同一种任意三角形、四边形可否镶
嵌成一个平面?问题用同一种平面图形如果不能密铺,用两种或者两种以上平面图形能不能密铺呢?做一做下列不同正多边形能否镶嵌?
正三角形与正方形?
正三角形与正五边形?
正三角形与正六边形?
正四边形与正六边形?
正三角形与正十二边形?正三角形与正方形∴2m+3n=12m=3
n=2设在一个顶点周围有 m个正三角
形的角,n个正方形的角,则有
∵ m,n 为正整数∴解为1)正三角形与正方形镶嵌图案设计2)正三角形与正六边形镶嵌图案设计∴m+2 n=6m=2
n=2m=4
n=1设在一个顶点周围有 m 个正三角形的角,
n 个正六边形的角,则有∵ m,n 为正整数∴解为4)正四边形
与正八边形5)正三角形与
正十二边形3)正五边形
与正十边形图案设计设在一个顶点周围有 m 个正五边形的角,n 个正十边形的角,则有∴3m+4n=10m=2
n=1∵ m,n 为正整数∴解为∴2m+3n=8m=1
n=2设在一个顶点周围有个 m 正四边形的角,
n 个正八边形的角,则有∵ m,n 为正整数∴解为用三种正多边形镶嵌,哪些能镶嵌成一个平面?探究问题(三)1、正六边形、正方形和正三角形的组合。2、正十二边形、正六边形和正方形的组合。 归纳三种不同正多边形进行镶嵌:
正三角形、正方形与正六边形,
正方形、正六边形与正十二边形。正三角形、正方形与正六边形正方形、正六边形与正十二边形
这节课你有哪些收获? 当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个平面图形。正三角形与正方形正三角形正方形正六边形正三角形与正六边形正三角形与正十二边形正三角形、正方形与正六边形正方形、正六边形
与正十二边形正五边形与正十边形
正四边形与正八边形
1、下列多边形一定不能进行平面镶嵌的是( )
A.三角形 B.正方形 C.任意四边形 D.正八边形 2、用正方形一种图形进行平面镶嵌时,在它的一个顶点周围的正方形的个数是( ) A.3 B.4 C.5 D.6 3、如果只用一种正多边形作平面镶嵌,而且在每一个正多边形的每一个顶点周围都有6个正多边形,则该正多边形的边数为( ) A.3 B.4 C.5 D.6DBA练习观察思考镶嵌图案欣赏
