数学:14.1《平面及其基本性质》教案(2)(沪教版高三上)
文档属性
| 名称 | 数学:14.1《平面及其基本性质》教案(2)(沪教版高三上) |  | |
| 格式 | rar | ||
| 文件大小 | 53.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-22 18:41:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
14.1 (2)平面及其基本性质
——三个公理三个推论
上海市南洋中学 金霞
一、教学内容分析
本节的重点和难点是三个公理三个推论.三个公理和三个推论是立体几何的基础,公理1确定直线在平面上;公理2明确两平面相交于一直线;公理3及三个推论给出了确定平面的条件.这些是后面学习空间直线与平面位置关系的基础.所以让学生透彻理解这些公理和性质,把现实中的具体空间问题抽象出来,初步认识直线与平面、平面与平面之间的关系并体会立体几何的基本思想,从而培养学生的空间想象能力,有利于学生更快更好的学习立体几何.
二、教学目标设计
理解平面的基本性质,能用三个公理三个推论解决简单的空间线面问题;了解一些简单的证明.培养空间想象能力,提高学习数学的自觉性和兴趣.
三、教学重点及难点
三个公理,三个推论.
四、教学过程设计
一、讲授新课
(一)公理1
如果直线上有两个点在平面上,那么直线在平面上.
(直线在平面上)
用集合语言表述:
(二)公理2
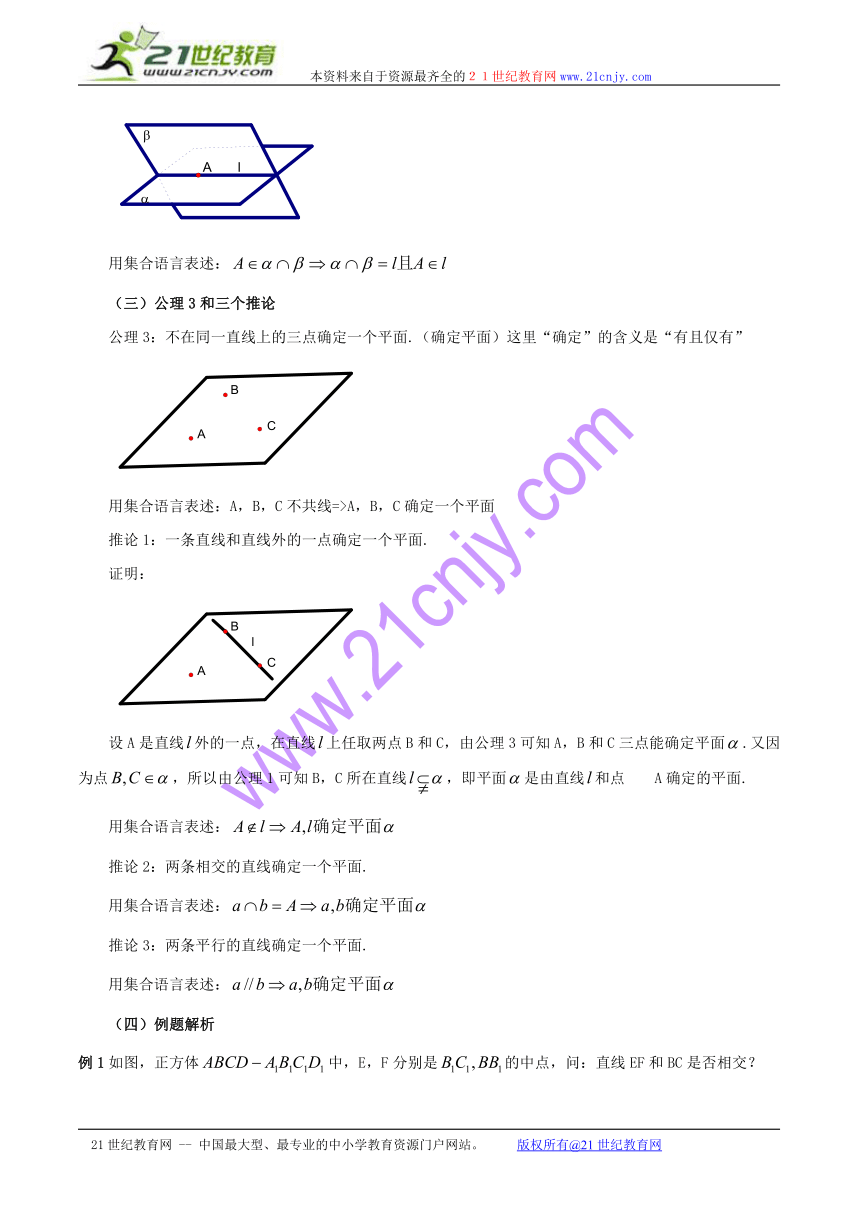
如果不同的两个平面、有一个公共点A,那么、的交集是过点A的直线.(平面与平面相交)
用集合语言表述:
(三)公理3和三个推论
公理3:不在同一直线上的三点确定一个平面.(确定平面)这里“确定”的含义是“有且仅有”
用集合语言表述:A,B,C不共线=>A,B,C确定一个平面
推论1:一条直线和直线外的一点确定一个平面.
证明:
设A是直线外的一点,在直线上任取两点B和C,由公理3可知A,B和C三点能确定平面.又因为点,所以由公理1可知B,C所在直线,即平面是由直线和点 A确定的平面.
用集合语言表述:
推论2:两条相交的直线确定一个平面.
用集合语言表述:
推论3:两条平行的直线确定一个平面.
用集合语言表述:
(四)例题解析
例1如图,正方体中,E,F分别是的中点,问:直线EF和BC是否相交?
如果相交,交点在那个平面内?
解:
又,则直线EF和BC共面;
设直线EF和BC相交于点p,则p在直线BC上,即点P在平面ABCD上.
[说明]利用公理1确定直线在平面内.
例2 如图,若,求证:直线C必过点P.
解:
[结论]三个平面两两相交得到三条交线,若其中两条交于一点,另一条必过此公共点.
例3 空间三个点能确定几个平面?
空间四个点能确定几个平面?
解:三点共线有无数多个平面;三点不共线可以确定一个平面.所以三点可以确定一个或无数个平面.
四点共线有无数个平面;有三点共线可确定一个平面;任意三点不共线能确定1个或3个平面.所以四点可以确定1个或3个或无数个平面.
[说明]公理3的简单应用.
例4空间三条直线相交于一点,可以确定几个平面?
空间四条直线相交于一点,可以确定几个平面?
解:三条直线相交于一点可以确定1个或3个平面;
四条直线相交于一点可以确定1个、4个或6个平面.
[说明]推论2的简单应用.
例5 如图,AB//CD,,求作BC与平面的交点.
解:连接EF和BC,交点即为所求BC与平面的交点.(公理3和公理2)
[说明]推论3的简单应用.
三、课堂小结
1.公理1:确定直线在平面内;
2.公理2:平面与平面相交于一直线;
3.公理3和三个推论确定平面的条件;
四、课后作业
练习14.1(1)2
练习14.1(2)1,2,3
五、教学设计说明
本章呈现了几何研究的范围从平面扩展到空间时的基本方法.把几何研究的范围从平面扩展到空间后,增加了新的对象——平面.空间几何学是平面几何学的推广,平面几何中研究点与点、点与直线、直线与直线三种位置关系;空间几何中则增加了点与平面、直线与平面、平面与平面三中位置关系.本节的主要内容是让学生理解三个公理和三个推论,运用这些公理和推论进行一些简单的证明.
公理是人们在长期的生活实践的观察和检验中发现的.可以联系生活中的情景来学习三个公理,从而帮助学生学习,加深他们对公理的理解.三个公理和三个推论是空间几何学习的基础,有了这个基础,才能进一步研究空间中点与面、线与面、面与面的位置关系和度量问题.
α
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
14.1 (2)平面及其基本性质
——三个公理三个推论
上海市南洋中学 金霞
一、教学内容分析
本节的重点和难点是三个公理三个推论.三个公理和三个推论是立体几何的基础,公理1确定直线在平面上;公理2明确两平面相交于一直线;公理3及三个推论给出了确定平面的条件.这些是后面学习空间直线与平面位置关系的基础.所以让学生透彻理解这些公理和性质,把现实中的具体空间问题抽象出来,初步认识直线与平面、平面与平面之间的关系并体会立体几何的基本思想,从而培养学生的空间想象能力,有利于学生更快更好的学习立体几何.
二、教学目标设计
理解平面的基本性质,能用三个公理三个推论解决简单的空间线面问题;了解一些简单的证明.培养空间想象能力,提高学习数学的自觉性和兴趣.
三、教学重点及难点
三个公理,三个推论.
四、教学过程设计
一、讲授新课
(一)公理1
如果直线上有两个点在平面上,那么直线在平面上.
(直线在平面上)
用集合语言表述:
(二)公理2
如果不同的两个平面、有一个公共点A,那么、的交集是过点A的直线.(平面与平面相交)
用集合语言表述:
(三)公理3和三个推论
公理3:不在同一直线上的三点确定一个平面.(确定平面)这里“确定”的含义是“有且仅有”
用集合语言表述:A,B,C不共线=>A,B,C确定一个平面
推论1:一条直线和直线外的一点确定一个平面.
证明:
设A是直线外的一点,在直线上任取两点B和C,由公理3可知A,B和C三点能确定平面.又因为点,所以由公理1可知B,C所在直线,即平面是由直线和点 A确定的平面.
用集合语言表述:
推论2:两条相交的直线确定一个平面.
用集合语言表述:
推论3:两条平行的直线确定一个平面.
用集合语言表述:
(四)例题解析
例1如图,正方体中,E,F分别是的中点,问:直线EF和BC是否相交?
如果相交,交点在那个平面内?
解:
又,则直线EF和BC共面;
设直线EF和BC相交于点p,则p在直线BC上,即点P在平面ABCD上.
[说明]利用公理1确定直线在平面内.
例2 如图,若,求证:直线C必过点P.
解:
[结论]三个平面两两相交得到三条交线,若其中两条交于一点,另一条必过此公共点.
例3 空间三个点能确定几个平面?
空间四个点能确定几个平面?
解:三点共线有无数多个平面;三点不共线可以确定一个平面.所以三点可以确定一个或无数个平面.
四点共线有无数个平面;有三点共线可确定一个平面;任意三点不共线能确定1个或3个平面.所以四点可以确定1个或3个或无数个平面.
[说明]公理3的简单应用.
例4空间三条直线相交于一点,可以确定几个平面?
空间四条直线相交于一点,可以确定几个平面?
解:三条直线相交于一点可以确定1个或3个平面;
四条直线相交于一点可以确定1个、4个或6个平面.
[说明]推论2的简单应用.
例5 如图,AB//CD,,求作BC与平面的交点.
解:连接EF和BC,交点即为所求BC与平面的交点.(公理3和公理2)
[说明]推论3的简单应用.
三、课堂小结
1.公理1:确定直线在平面内;
2.公理2:平面与平面相交于一直线;
3.公理3和三个推论确定平面的条件;
四、课后作业
练习14.1(1)2
练习14.1(2)1,2,3
五、教学设计说明
本章呈现了几何研究的范围从平面扩展到空间时的基本方法.把几何研究的范围从平面扩展到空间后,增加了新的对象——平面.空间几何学是平面几何学的推广,平面几何中研究点与点、点与直线、直线与直线三种位置关系;空间几何中则增加了点与平面、直线与平面、平面与平面三中位置关系.本节的主要内容是让学生理解三个公理和三个推论,运用这些公理和推论进行一些简单的证明.
公理是人们在长期的生活实践的观察和检验中发现的.可以联系生活中的情景来学习三个公理,从而帮助学生学习,加深他们对公理的理解.三个公理和三个推论是空间几何学习的基础,有了这个基础,才能进一步研究空间中点与面、线与面、面与面的位置关系和度量问题.
α
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
