数学:14.1《平面及其基本性质》课件(3)(沪教版高三上)
文档属性
| 名称 | 数学:14.1《平面及其基本性质》课件(3)(沪教版高三上) |

|
|
| 格式 | rar | ||
| 文件大小 | 297.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-22 00:00:00 | ||
图片预览





文档简介
课件12张PPT。三个公理及三个推论的应用南洋中学 马亚萍练习(1)若A∈平面α,B∈平面α,C∈直线AB,则(2)下列命题正确的是( )
A.两组对边分别相等的四边形是平行四边形
B.四条线段顺次首尾连接所构成的图形一定是平面图形;
C.三条互相平行的直线一定共面;
D.梯形是平面图形②两个平面可能只有一个公共点.③四条边都相等的四边形是菱形.①若直线 与平面 有公共点,则称④⑤若4点不共面,则它们任意三点都不共线 ⑥两两相交的三条直线必定共面 (3) 判断题××××√×3或48,4,6或7(4)不在同一直线上的五个点,能确定
平面的最多个数是( )
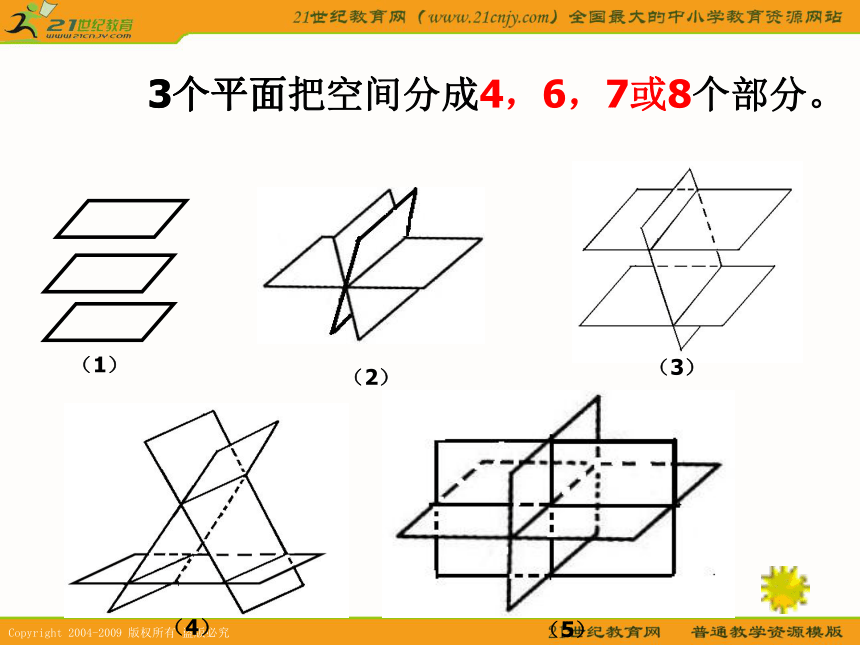
A.8个,B.9个,C.10个, D.12个2个平面分空间有两种情况:两个平面把空间分成3或4个部分。(1)两平面没有公共点时(2)两平面有公共点时3个平面(2)(3)(4)(5)3个平面把空间分成4,6,7或8个部分。1、共面问题例1:已知直线l1,l2和l3两两相交,且三线不共点,求证:直线l1,l2和l3在同一平面上。练习:如果四条直线两两相交,且无三线共点呢? 归一法例2:已知a∥b∥c,d与a,b,c分别交于A,B,C.求证:a,b,c,d共面。 2、三点共线例3:在正方体ABCD-A1B1C1D1中,P,Q,R分别在棱AB,BB1,CC1上,且DP,QR相交于O,求证:OBC三点共线.提示:要证明各点共线,只要证明它们是两个平面的公共点例4、已知 求证: P,Q,R三点共线 ACBPQR3、三线共点结论 : 三个平面两两相交于三条直线,若三条直线不平,则它们相交于一点.例4:空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,已知EF与HG相交于Q点,求证:EF,HG,AC三线共点.提示:要证明各线共点,只要证明两线相交一点,而这个点在交线上,即第三条直线.(2)公理2: “共点”、“共线”、 “共面”问题(3)公理3, 推论1、2、3:理论依据:(1)公理1:判定两平证点、线共面的依据,确定平面也是作辅助面的依据面相交(“点共线”,
“线共点”)判断或证明直线是否在平面内确定两个平面的交线,
A.两组对边分别相等的四边形是平行四边形
B.四条线段顺次首尾连接所构成的图形一定是平面图形;
C.三条互相平行的直线一定共面;
D.梯形是平面图形②两个平面可能只有一个公共点.③四条边都相等的四边形是菱形.①若直线 与平面 有公共点,则称④⑤若4点不共面,则它们任意三点都不共线 ⑥两两相交的三条直线必定共面 (3) 判断题××××√×3或48,4,6或7(4)不在同一直线上的五个点,能确定
平面的最多个数是( )
A.8个,B.9个,C.10个, D.12个2个平面分空间有两种情况:两个平面把空间分成3或4个部分。(1)两平面没有公共点时(2)两平面有公共点时3个平面(2)(3)(4)(5)3个平面把空间分成4,6,7或8个部分。1、共面问题例1:已知直线l1,l2和l3两两相交,且三线不共点,求证:直线l1,l2和l3在同一平面上。练习:如果四条直线两两相交,且无三线共点呢? 归一法例2:已知a∥b∥c,d与a,b,c分别交于A,B,C.求证:a,b,c,d共面。 2、三点共线例3:在正方体ABCD-A1B1C1D1中,P,Q,R分别在棱AB,BB1,CC1上,且DP,QR相交于O,求证:OBC三点共线.提示:要证明各点共线,只要证明它们是两个平面的公共点例4、已知 求证: P,Q,R三点共线 ACBPQR3、三线共点结论 : 三个平面两两相交于三条直线,若三条直线不平,则它们相交于一点.例4:空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,已知EF与HG相交于Q点,求证:EF,HG,AC三线共点.提示:要证明各线共点,只要证明两线相交一点,而这个点在交线上,即第三条直线.(2)公理2: “共点”、“共线”、 “共面”问题(3)公理3, 推论1、2、3:理论依据:(1)公理1:判定两平证点、线共面的依据,确定平面也是作辅助面的依据面相交(“点共线”,
“线共点”)判断或证明直线是否在平面内确定两个平面的交线,
