4.6 利用相似三角形测高 同步练习(含部分答案)
文档属性
| 名称 | 4.6 利用相似三角形测高 同步练习(含部分答案) |  | |
| 格式 | zip | ||
| 文件大小 | 241.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-13 07:45:37 | ||
图片预览

文档简介
4.6
利用相似三角形测高
同步练习
一、教材题目:P105,T1-T4
1.高4m的旗杆在水平地面上的影子长6m,此时测得附近一个建筑物的影子长24m,求该建筑物的高度。
2.旗杆的影子长6m,同时测得旗杆顶端到其影子顶端的距离是10m,如果此时附近小树的影子长3m,那么小树有多高?
3.一盗窃犯于夜深人静之时潜入某单位作案,该单位的自动摄像系统摄下了他作案的全过程。请你为警方设计一个方案,估计该盗窃犯的大致身高。
4.如图,AB表示一个窗户的高,AM和BN表示射入室内的光线,窗户的下端到地面的距离BC=1m。已知某一时刻BC=1m在地面的影长CN=1.5Mm,AC在地面的影长CM=4.5m,求窗户的高度.
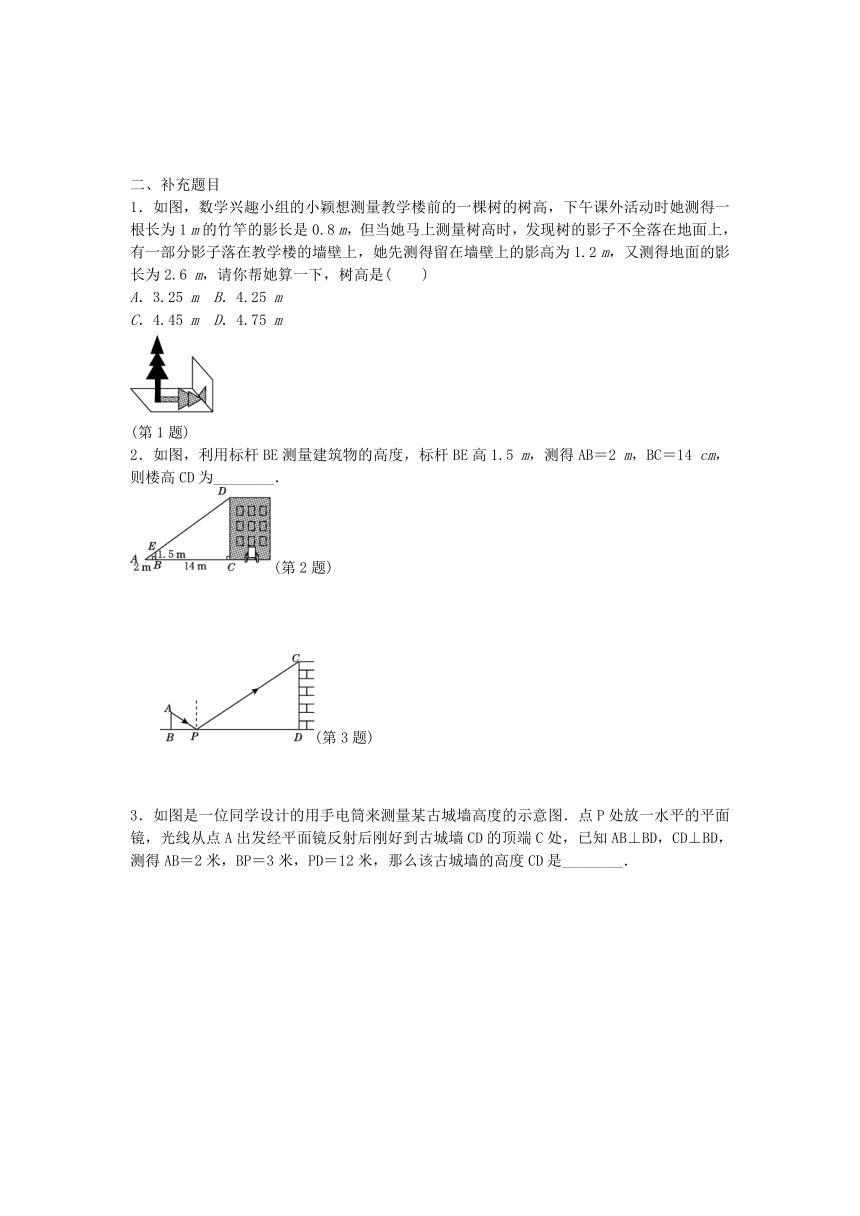
二、补充题目
1.如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1
m的竹竿的影长是0.8
m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,她先测得留在墙壁上的影高为1.2
m,又测得地面的影长为2.6
m,请你帮她算一下,树高是( )
A.3.25
m
B.4.25
m
C.4.45
m
D.4.75
m
(第1题)
2.如图,利用标杆BE测量建筑物的高度,标杆BE高1.5
m,测得AB=2
m,BC=14
cm,则楼高CD为________.
(第2题)
(第3题)
3.如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=2米,BP=3米,PD=12米,那么该古城墙的高度CD是________.
4.如图,AB是斜靠在墙上的长梯,梯脚B距墙脚1.6m,梯上点D距墙1.4m,BD长0.55m,求该梯子的长。
5、如图,一圆柱形油桶,高1.5米,用一根长2米的木棒从桶盖小口A处斜插桶内另一端的B处,抽出木棒后,量得上面没浸油的部分为1.2米,求桶内油面的高度.
6.如图,小明站在处看甲乙两楼楼顶上的点和点.三点在同一条直线上,点分别在点的正下方且三点在同一条直线上.相距米,相距米,乙楼高为米,甲楼高为多少米(小明身高忽略不计)
7.马戏团让狮子和公鸡表演跷跷板节目.跷跷板支柱AB的高度为1.2米.
(1)若吊环高度为2米,支点A为跷跷板PQ的中点,狮子能否将公鸡送到吊环上?为什么?
若吊环高度为3.6米,在不改变其他条件的前提下移动支柱,当支点A移到跷跷板PQ的什么位置时,狮子刚好能将公鸡送到吊环上?
答案
教材
1.解:设该建筑物的高度为x
m,根据题意,得=,x==16,所以该建筑物的高度为16
m.
2.解:设小树有x
m高,则树顶到树影顶端的距离是
m.根据题意,得=,即x2=16,所以x1=4,x2=-4(舍去),所以小树有4
m高.
3.解:以现场的某实物为参照物,测量出该实物的高度,摄像中盗窃犯的影长以及该实物的影长,根据=,可估计出该盗窃犯的大致身高.
4.解:易知NB∥MA,∴=.∴AC===3(m).∴AB=AC-BC=3-1=2(m),即窗户的高度为2
m.
(第2题)
1.C 点拨:如图,设BD是BC在地面上的影子,树高为x
m,
根据竹竿的高与其影子的比值和树高与其影子的比值相同,得=,而CB=1.2
m,∴BD=0.96
m.
∴树在地面上的实际影子长是0.96+2.6=3.56(m).
又∵竹竿的高与其影子的比值和树高与其影子的比值相同,∴=.
∴x=4.45.∴树高是4.45
m.
2.12
m
3.
6.8米
4-7答案略
甲
乙
利用相似三角形测高
同步练习
一、教材题目:P105,T1-T4
1.高4m的旗杆在水平地面上的影子长6m,此时测得附近一个建筑物的影子长24m,求该建筑物的高度。
2.旗杆的影子长6m,同时测得旗杆顶端到其影子顶端的距离是10m,如果此时附近小树的影子长3m,那么小树有多高?
3.一盗窃犯于夜深人静之时潜入某单位作案,该单位的自动摄像系统摄下了他作案的全过程。请你为警方设计一个方案,估计该盗窃犯的大致身高。
4.如图,AB表示一个窗户的高,AM和BN表示射入室内的光线,窗户的下端到地面的距离BC=1m。已知某一时刻BC=1m在地面的影长CN=1.5Mm,AC在地面的影长CM=4.5m,求窗户的高度.
二、补充题目
1.如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1
m的竹竿的影长是0.8
m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,她先测得留在墙壁上的影高为1.2
m,又测得地面的影长为2.6
m,请你帮她算一下,树高是( )
A.3.25
m
B.4.25
m
C.4.45
m
D.4.75
m
(第1题)
2.如图,利用标杆BE测量建筑物的高度,标杆BE高1.5
m,测得AB=2
m,BC=14
cm,则楼高CD为________.
(第2题)
(第3题)
3.如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=2米,BP=3米,PD=12米,那么该古城墙的高度CD是________.
4.如图,AB是斜靠在墙上的长梯,梯脚B距墙脚1.6m,梯上点D距墙1.4m,BD长0.55m,求该梯子的长。
5、如图,一圆柱形油桶,高1.5米,用一根长2米的木棒从桶盖小口A处斜插桶内另一端的B处,抽出木棒后,量得上面没浸油的部分为1.2米,求桶内油面的高度.
6.如图,小明站在处看甲乙两楼楼顶上的点和点.三点在同一条直线上,点分别在点的正下方且三点在同一条直线上.相距米,相距米,乙楼高为米,甲楼高为多少米(小明身高忽略不计)
7.马戏团让狮子和公鸡表演跷跷板节目.跷跷板支柱AB的高度为1.2米.
(1)若吊环高度为2米,支点A为跷跷板PQ的中点,狮子能否将公鸡送到吊环上?为什么?
若吊环高度为3.6米,在不改变其他条件的前提下移动支柱,当支点A移到跷跷板PQ的什么位置时,狮子刚好能将公鸡送到吊环上?
答案
教材
1.解:设该建筑物的高度为x
m,根据题意,得=,x==16,所以该建筑物的高度为16
m.
2.解:设小树有x
m高,则树顶到树影顶端的距离是
m.根据题意,得=,即x2=16,所以x1=4,x2=-4(舍去),所以小树有4
m高.
3.解:以现场的某实物为参照物,测量出该实物的高度,摄像中盗窃犯的影长以及该实物的影长,根据=,可估计出该盗窃犯的大致身高.
4.解:易知NB∥MA,∴=.∴AC===3(m).∴AB=AC-BC=3-1=2(m),即窗户的高度为2
m.
(第2题)
1.C 点拨:如图,设BD是BC在地面上的影子,树高为x
m,
根据竹竿的高与其影子的比值和树高与其影子的比值相同,得=,而CB=1.2
m,∴BD=0.96
m.
∴树在地面上的实际影子长是0.96+2.6=3.56(m).
又∵竹竿的高与其影子的比值和树高与其影子的比值相同,∴=.
∴x=4.45.∴树高是4.45
m.
2.12
m
3.
6.8米
4-7答案略
甲
乙
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
