1.1 锐角三角函数 学案4(无答案)
文档属性
| 名称 | 1.1 锐角三角函数 学案4(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 261.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-13 00:00:00 | ||
图片预览



文档简介
1.1
锐角三角函数(第一课时)学案
学习目标:
1.经历探索直角三角形中边角关系的过程,理解正切的意义和与现实生活的联系;
2.能用表示直角三角形中两直角边的比,表示物体的倾斜程度和坡度(坡比)等;
3.能根据直角三角形的边角关系,用正切进行简单的计算。
模块一:自主学习
学习内容
摘
记
温故知新1.在Rt△ABC中,∠B=53°,∠C=90°,
则∠A=
;2.在Rt△ABC中,∠C=90°,BC=24cm,AB=26cm,则AC=
;3.在△ABC中,BC=7cm,
AC=24cm,AB=25cm,则△ABC是
三角形。请你阅读课本P2至P4,然后完成以下问题:比较梯子的倾斜程度(1)如图,这里摆放的三对梯子,比较每对梯子中哪一个更陡?梯子的倾斜程度与什么有关?(2)分别求出每幅图中的与,想一想它们的比值与梯子的倾斜程度有什么关系?
如图1-4,小明想通过测量及,算出它们的比,来说明梯子的倾斜程度;而小亮则认为通过测量及
,算出它们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗?(1)和有什么关系?(2)和有什么关系?(3)如果改变在梯子上的位置呢?
由此你得出什么结论?
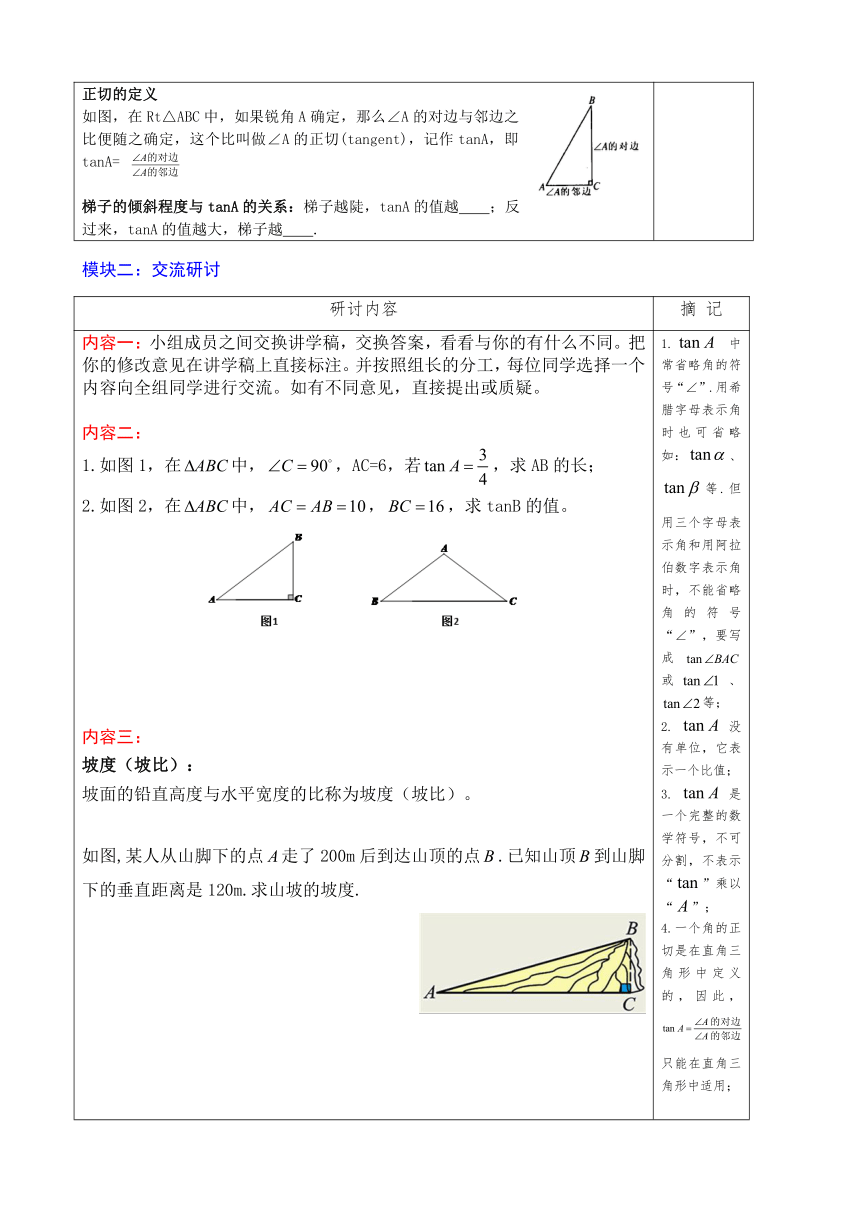
正切的定义如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边之比便随之确定,这个比叫做∠A的正切(tangent),记作tanA,即tanA=梯子的倾斜程度与tanA的关系:梯子越陡,tanA的值越
;反过来,tanA的值越大,梯子越
.
模块二:交流研讨
研讨内容
摘
记
内容一:小组成员之间交换讲学稿,交换答案,看看与你的有什么不同。把你的修改意见在讲学稿上直接标注。并按照组长的分工,每位同学选择一个内容向全组同学进行交流。如有不同意见,直接提出或质疑。内容二:1.如图1,在中,,AC=6,若,求AB的长;
2.如图2,在中,,,求tanB的值。
内容三:坡度(坡比):坡面的铅直高度与水平宽度的比称为坡度(坡比)。如图 ,某人从山脚下的点走了200m后到达山顶的点.已知山顶到山脚下的垂直距离是120m.求山坡的坡度.
1.
中常省略角的符号“∠”.用希腊字母表示角时也可省略如:、等.但用三个字母表示角和用阿拉伯数字表示角时,不能省略角的符号“∠”,要写成或、等;2.没有单位,它表示一个比值;3.是一个完整的数学符号,不可分割,不表示“”乘以“”;4.一个角的正切是在直角三角形中定义的,因此,只能在直角三角形中适用;
1.1
锐角三角函数(第一课时)
练习
一、基础题
1.若锐角α>β,则tanα
tanβ(填“﹥”或“﹤”)
2.在△ABC中,AB=3,AC=4,BC=5,则tanB=_______。
3.在△ABC中,AB=AC=3,BC=4,则tanC=______。
4.在Rt△ABC中,∠C=90°,则tanA与tanB的关系是
。
5.
菱形的两条对角线分别是16和12.较长的一条对角线与菱形的一边的夹角为θ,则tanθ=
。
6.在Rt△ABC中,∠C=90°,AB=3,BC=1,则tanA=
_______。
二、发展题
7.已知等腰三角形的一条腰长为
20
cm,底边长为
24
cm,求底角的正切值。
8.在∠ABC中,∠C=90°,BC=10cm,AB=26
cm,求
tan
A和
tan
B的值.
三、提高题
9.如图,为拦水坝的横截面,其中AB面的坡度i=,若坝高BC=20米,求坝面AB的长.
1.1
锐角三角函数(第二课时)学案
学习目标:
1.能利用相似的直角三角形,探索并认识锐角三角函数——正弦、余弦,理解锐角的正弦与余弦和梯子倾斜程度的关系;
2.能够用sinA,cosA表示直角三角形中直角边与斜边的比,能用正弦、余弦进行简单的计算。
模块一:自主学习
学习内容
摘
记
温故知新1.如图,Rt△ABC中,tanA
=
,tanB=
.2.在Rt△ABC中,∠C=90°,tanA=,AC=10,则BC=
,AB=
.3.若梯子与水平面相交的锐角(倾斜角)为∠A,∠A越大,梯子越
;tanA的值越大,梯子越
.请你阅读课本P5至P6,然后完成以下问题:锐角的正弦与余弦已知,如图:(1)Rt△AB1C1和Rt△AB2C2的关系是
;(2)和的关系是
;(3)如果改变B2在斜边上的位置,则和的关系是
;(4)从以上的问题可以看出:当直角三角形的一个锐角的大小已确定时,它的对边与斜边的比值__________,它的邻边与斜边的比值__________。正弦的定义:如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的对边BC与斜边AB的比叫做∠A的正弦,记作sinA,即sinA=________.余弦的定义:如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的邻边AC与斜边AB的比叫做∠A的余弦,记作cosA,即cosA=
.锐角A的正弦,余弦,正切都是∠A的三角函数.梯子的倾斜程度角与tanA,sinA和cosA之间的关系:tanA越大,梯子
;sinA越大,梯子
;
cosA越
,梯子越陡。
(1)sinA,cosA是在直角三角形中定义的,∠A是一个锐角;(2)sinA,cosA中常省去符号“∠”.但∠BAC的正弦和余弦表示为:
sin∠BAC,cos∠BAC.∠1的正弦和余弦表示为:
sin∠1,cos∠1;(3)sinA,cosA没有单位,它表示一个值;(4)sinA,cosA是一个完整的符号,不表示“sin”,“cos”乘以“A”
;(5)sinA,cosA的大小只与∠A的大小有关,而与直角三角形的边长没有必然的关系.
模块二:交流研讨
研讨内容
摘
记
内容一:小组成员之间交换讲学稿,交换答案,看看与你的有什么不同。把你的修改意见在讲学稿上直接标注。并按照组长的分工,每位同学选择一个内容向全组同学进行交流。如有不同意见,直接提出或质疑。内容二:如图,在Rt△ABC中,∠C=90°,AB=20,sinA=0.6.(1)求BC、cosA和cosB的值;(2)sinA与cosB有什么关系 sinA与cosA呢?内容三如图,在等腰△ABC中,AB=AC=5,BC=6.(1)求sinB,cosB,tanB的值;(2)求AB边上的高.
结论:1.在直角三角形中,一个锐角的正弦等于另一个锐角的
.2.在直角三角形中,一个锐角的正弦与余弦的平方和等于
.
模块三:巩固内化
学习内容
摘
记
任务:尝试完成下列习题。如图,在Rt△ABC中,∠C=90°,cosA=,BC=10.求AB和sinB的值;
1.1
锐角三角函数(第二课时)练习
一、基础题
1.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值(
)
A、扩大100倍
B、缩小100倍
C、不变
D、不能确定
2.已知∠A,∠B为锐角
(1)若∠A=∠B,则sinA
sinB;
(2)若sinA=sinB,则∠A
∠B.
3.如图,
∠ACB=90°,CD⊥AB,sinB=(
)=(
)=(
)
二、发展题
4.如图,在Rt△ABC中,∠C=90°,
AC=4,AB=6,求∠B的三个三角函数值.
5.如图,在Rt△ABC中,∠C=90°,BC=6,sinB=0.8,求AC和AB.
三、提高题
6.在Rt△ABC中,∠BCA=90°,CD是斜边AB上的中线,BC=8,CD=5.求sin∠ACD,cos∠ACD和tan∠ACD.
1.1.3
30°,45°,60°角的三角函数值
(第三课时)学案
学习目标:
1.经历探索30°,45°,60°角的三角函数值的过程,能够进行有关的推理,进一步体会三角函数的意义;
2.能进行含有30°,45°,60°角的三角函数值的计算;
3.能根据30°,45°,60°的三角函数值说明相应的锐角的度数。
模块一:自主学习
学习内容
摘
记
温故知新如图所示
在
Rt△ABC中,∠C=90°.(1)a、b、c三者之间的关系是
,∠A+∠B=
.(2)sinA=
,cosA=
,tanA=
.(3)sinB=
,cosB=
,tanB=
.请你阅读课本P8至P9,然后完成以下问题:30°和60°角的三角函数值(1)观察一副三角尺,其中有几个锐角 它们分别等于多少度 (2)
sin30°等于多少呢 (3)
cos30°等于多少 tan30°呢 (4)
sin60°,cos60°和tan60°等于多少?45°角的三角函数值(1)观察一副三角尺,其中有几个锐角 它们都等于多少度 (2)
sin45°等于多少呢 (3)
cos45°等于多少 tan45°呢
模块二:交流研讨
研讨内容
摘
记
内容一:小组成员之间交换讲学稿,交换答案,看看与你的有什么不同。把你的修改意见在讲学稿上直接标注。并按照组长的分工,每位同学选择一个内容向全组同学进行交流。如有不同意见,直接提出或质疑。内容二:(1)sin60°-cos45°;
(2)cos60°+tan60°
内容三
一个小孩荡秋千,秋千链子的长度为2m,当秋千向两边摆动时,摆角恰好为60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差.
模块三:巩固内化
学习内容
摘
记
任务:尝试完成下列习题。如图,为了测量河的宽度,在河边选定一点C,使它正对着对岸的一个目标B,然后沿着河岸走100米到点A(∠ACB=90°),测得∠CAB=45°.问河宽是多少?
1.1.3
30°,45°,60°角的三角函数值
练习
一、基础题
1.在
Rt△ABC中,∠C=90°.
(1)若∠A=30°,则sinA=
,cosA=
,tanA=
.
(2)若sinA=,则∠A=
,∠B=
.
(3)若tanA=1,则∠A=
.
2.在
△ABC中,∠C=90°,∠B=2∠A,则tanA=
3.在△ABC中,若cosA=,tanB=,则∠C
=
4.(1)·
(2)
二、发展题
5.如图,身高1.7m的小丽用一个两锐角分别为30°和60°的三角尺测量一棵树的高度(∠A=30°),已知她与树之间的距离为5m.那么这棵树大约有多高
三、提高题
6.某阶梯的形状如图所示,其中线段AB=BC,AB部分的坡角为45°,BC部分的坡角为30°,AD=m.如果每个台阶的高是20cm,那么这一阶梯约有多少个台阶 (取1.4)
图1—4
锐角三角函数(第一课时)学案
学习目标:
1.经历探索直角三角形中边角关系的过程,理解正切的意义和与现实生活的联系;
2.能用表示直角三角形中两直角边的比,表示物体的倾斜程度和坡度(坡比)等;
3.能根据直角三角形的边角关系,用正切进行简单的计算。
模块一:自主学习
学习内容
摘
记
温故知新1.在Rt△ABC中,∠B=53°,∠C=90°,
则∠A=
;2.在Rt△ABC中,∠C=90°,BC=24cm,AB=26cm,则AC=
;3.在△ABC中,BC=7cm,
AC=24cm,AB=25cm,则△ABC是
三角形。请你阅读课本P2至P4,然后完成以下问题:比较梯子的倾斜程度(1)如图,这里摆放的三对梯子,比较每对梯子中哪一个更陡?梯子的倾斜程度与什么有关?(2)分别求出每幅图中的与,想一想它们的比值与梯子的倾斜程度有什么关系?
如图1-4,小明想通过测量及,算出它们的比,来说明梯子的倾斜程度;而小亮则认为通过测量及
,算出它们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗?(1)和有什么关系?(2)和有什么关系?(3)如果改变在梯子上的位置呢?
由此你得出什么结论?
正切的定义如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边之比便随之确定,这个比叫做∠A的正切(tangent),记作tanA,即tanA=梯子的倾斜程度与tanA的关系:梯子越陡,tanA的值越
;反过来,tanA的值越大,梯子越
.
模块二:交流研讨
研讨内容
摘
记
内容一:小组成员之间交换讲学稿,交换答案,看看与你的有什么不同。把你的修改意见在讲学稿上直接标注。并按照组长的分工,每位同学选择一个内容向全组同学进行交流。如有不同意见,直接提出或质疑。内容二:1.如图1,在中,,AC=6,若,求AB的长;
2.如图2,在中,,,求tanB的值。
内容三:坡度(坡比):坡面的铅直高度与水平宽度的比称为坡度(坡比)。如图 ,某人从山脚下的点走了200m后到达山顶的点.已知山顶到山脚下的垂直距离是120m.求山坡的坡度.
1.
中常省略角的符号“∠”.用希腊字母表示角时也可省略如:、等.但用三个字母表示角和用阿拉伯数字表示角时,不能省略角的符号“∠”,要写成或、等;2.没有单位,它表示一个比值;3.是一个完整的数学符号,不可分割,不表示“”乘以“”;4.一个角的正切是在直角三角形中定义的,因此,只能在直角三角形中适用;
1.1
锐角三角函数(第一课时)
练习
一、基础题
1.若锐角α>β,则tanα
tanβ(填“﹥”或“﹤”)
2.在△ABC中,AB=3,AC=4,BC=5,则tanB=_______。
3.在△ABC中,AB=AC=3,BC=4,则tanC=______。
4.在Rt△ABC中,∠C=90°,则tanA与tanB的关系是
。
5.
菱形的两条对角线分别是16和12.较长的一条对角线与菱形的一边的夹角为θ,则tanθ=
。
6.在Rt△ABC中,∠C=90°,AB=3,BC=1,则tanA=
_______。
二、发展题
7.已知等腰三角形的一条腰长为
20
cm,底边长为
24
cm,求底角的正切值。
8.在∠ABC中,∠C=90°,BC=10cm,AB=26
cm,求
tan
A和
tan
B的值.
三、提高题
9.如图,为拦水坝的横截面,其中AB面的坡度i=,若坝高BC=20米,求坝面AB的长.
1.1
锐角三角函数(第二课时)学案
学习目标:
1.能利用相似的直角三角形,探索并认识锐角三角函数——正弦、余弦,理解锐角的正弦与余弦和梯子倾斜程度的关系;
2.能够用sinA,cosA表示直角三角形中直角边与斜边的比,能用正弦、余弦进行简单的计算。
模块一:自主学习
学习内容
摘
记
温故知新1.如图,Rt△ABC中,tanA
=
,tanB=
.2.在Rt△ABC中,∠C=90°,tanA=,AC=10,则BC=
,AB=
.3.若梯子与水平面相交的锐角(倾斜角)为∠A,∠A越大,梯子越
;tanA的值越大,梯子越
.请你阅读课本P5至P6,然后完成以下问题:锐角的正弦与余弦已知,如图:(1)Rt△AB1C1和Rt△AB2C2的关系是
;(2)和的关系是
;(3)如果改变B2在斜边上的位置,则和的关系是
;(4)从以上的问题可以看出:当直角三角形的一个锐角的大小已确定时,它的对边与斜边的比值__________,它的邻边与斜边的比值__________。正弦的定义:如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的对边BC与斜边AB的比叫做∠A的正弦,记作sinA,即sinA=________.余弦的定义:如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的邻边AC与斜边AB的比叫做∠A的余弦,记作cosA,即cosA=
.锐角A的正弦,余弦,正切都是∠A的三角函数.梯子的倾斜程度角与tanA,sinA和cosA之间的关系:tanA越大,梯子
;sinA越大,梯子
;
cosA越
,梯子越陡。
(1)sinA,cosA是在直角三角形中定义的,∠A是一个锐角;(2)sinA,cosA中常省去符号“∠”.但∠BAC的正弦和余弦表示为:
sin∠BAC,cos∠BAC.∠1的正弦和余弦表示为:
sin∠1,cos∠1;(3)sinA,cosA没有单位,它表示一个值;(4)sinA,cosA是一个完整的符号,不表示“sin”,“cos”乘以“A”
;(5)sinA,cosA的大小只与∠A的大小有关,而与直角三角形的边长没有必然的关系.
模块二:交流研讨
研讨内容
摘
记
内容一:小组成员之间交换讲学稿,交换答案,看看与你的有什么不同。把你的修改意见在讲学稿上直接标注。并按照组长的分工,每位同学选择一个内容向全组同学进行交流。如有不同意见,直接提出或质疑。内容二:如图,在Rt△ABC中,∠C=90°,AB=20,sinA=0.6.(1)求BC、cosA和cosB的值;(2)sinA与cosB有什么关系 sinA与cosA呢?内容三如图,在等腰△ABC中,AB=AC=5,BC=6.(1)求sinB,cosB,tanB的值;(2)求AB边上的高.
结论:1.在直角三角形中,一个锐角的正弦等于另一个锐角的
.2.在直角三角形中,一个锐角的正弦与余弦的平方和等于
.
模块三:巩固内化
学习内容
摘
记
任务:尝试完成下列习题。如图,在Rt△ABC中,∠C=90°,cosA=,BC=10.求AB和sinB的值;
1.1
锐角三角函数(第二课时)练习
一、基础题
1.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值(
)
A、扩大100倍
B、缩小100倍
C、不变
D、不能确定
2.已知∠A,∠B为锐角
(1)若∠A=∠B,则sinA
sinB;
(2)若sinA=sinB,则∠A
∠B.
3.如图,
∠ACB=90°,CD⊥AB,sinB=(
)=(
)=(
)
二、发展题
4.如图,在Rt△ABC中,∠C=90°,
AC=4,AB=6,求∠B的三个三角函数值.
5.如图,在Rt△ABC中,∠C=90°,BC=6,sinB=0.8,求AC和AB.
三、提高题
6.在Rt△ABC中,∠BCA=90°,CD是斜边AB上的中线,BC=8,CD=5.求sin∠ACD,cos∠ACD和tan∠ACD.
1.1.3
30°,45°,60°角的三角函数值
(第三课时)学案
学习目标:
1.经历探索30°,45°,60°角的三角函数值的过程,能够进行有关的推理,进一步体会三角函数的意义;
2.能进行含有30°,45°,60°角的三角函数值的计算;
3.能根据30°,45°,60°的三角函数值说明相应的锐角的度数。
模块一:自主学习
学习内容
摘
记
温故知新如图所示
在
Rt△ABC中,∠C=90°.(1)a、b、c三者之间的关系是
,∠A+∠B=
.(2)sinA=
,cosA=
,tanA=
.(3)sinB=
,cosB=
,tanB=
.请你阅读课本P8至P9,然后完成以下问题:30°和60°角的三角函数值(1)观察一副三角尺,其中有几个锐角 它们分别等于多少度 (2)
sin30°等于多少呢 (3)
cos30°等于多少 tan30°呢 (4)
sin60°,cos60°和tan60°等于多少?45°角的三角函数值(1)观察一副三角尺,其中有几个锐角 它们都等于多少度 (2)
sin45°等于多少呢 (3)
cos45°等于多少 tan45°呢
模块二:交流研讨
研讨内容
摘
记
内容一:小组成员之间交换讲学稿,交换答案,看看与你的有什么不同。把你的修改意见在讲学稿上直接标注。并按照组长的分工,每位同学选择一个内容向全组同学进行交流。如有不同意见,直接提出或质疑。内容二:(1)sin60°-cos45°;
(2)cos60°+tan60°
内容三
一个小孩荡秋千,秋千链子的长度为2m,当秋千向两边摆动时,摆角恰好为60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差.
模块三:巩固内化
学习内容
摘
记
任务:尝试完成下列习题。如图,为了测量河的宽度,在河边选定一点C,使它正对着对岸的一个目标B,然后沿着河岸走100米到点A(∠ACB=90°),测得∠CAB=45°.问河宽是多少?
1.1.3
30°,45°,60°角的三角函数值
练习
一、基础题
1.在
Rt△ABC中,∠C=90°.
(1)若∠A=30°,则sinA=
,cosA=
,tanA=
.
(2)若sinA=,则∠A=
,∠B=
.
(3)若tanA=1,则∠A=
.
2.在
△ABC中,∠C=90°,∠B=2∠A,则tanA=
3.在△ABC中,若cosA=,tanB=,则∠C
=
4.(1)·
(2)
二、发展题
5.如图,身高1.7m的小丽用一个两锐角分别为30°和60°的三角尺测量一棵树的高度(∠A=30°),已知她与树之间的距离为5m.那么这棵树大约有多高
三、提高题
6.某阶梯的形状如图所示,其中线段AB=BC,AB部分的坡角为45°,BC部分的坡角为30°,AD=m.如果每个台阶的高是20cm,那么这一阶梯约有多少个台阶 (取1.4)
图1—4
