青年教师数学问题讲授核心片段展示人教版八年级数学(下册)勾股定理的证明课件(汕头市世贸实验学校) (共16张PPT)
文档属性
| 名称 | 青年教师数学问题讲授核心片段展示人教版八年级数学(下册)勾股定理的证明课件(汕头市世贸实验学校) (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-13 00:00:00 | ||
图片预览




文档简介
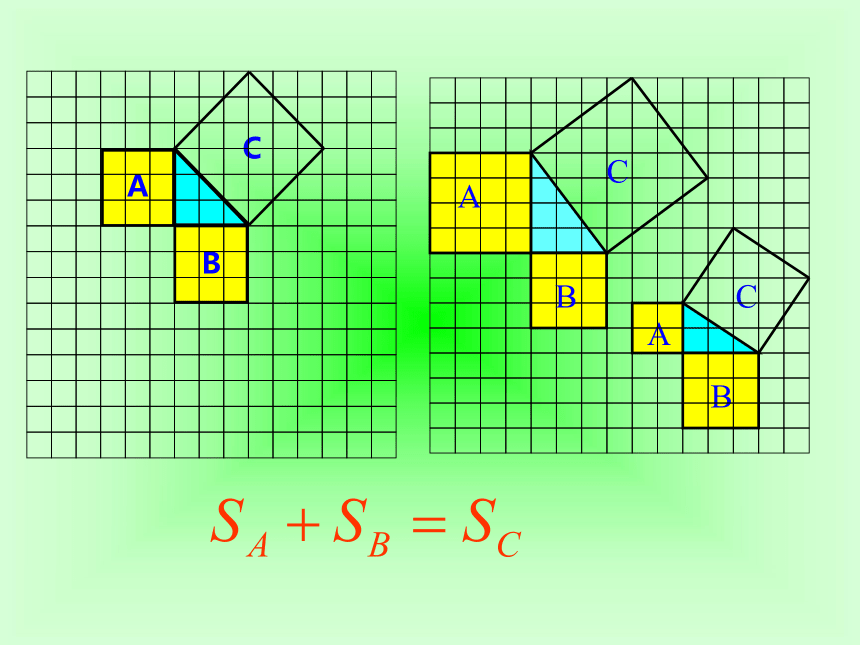
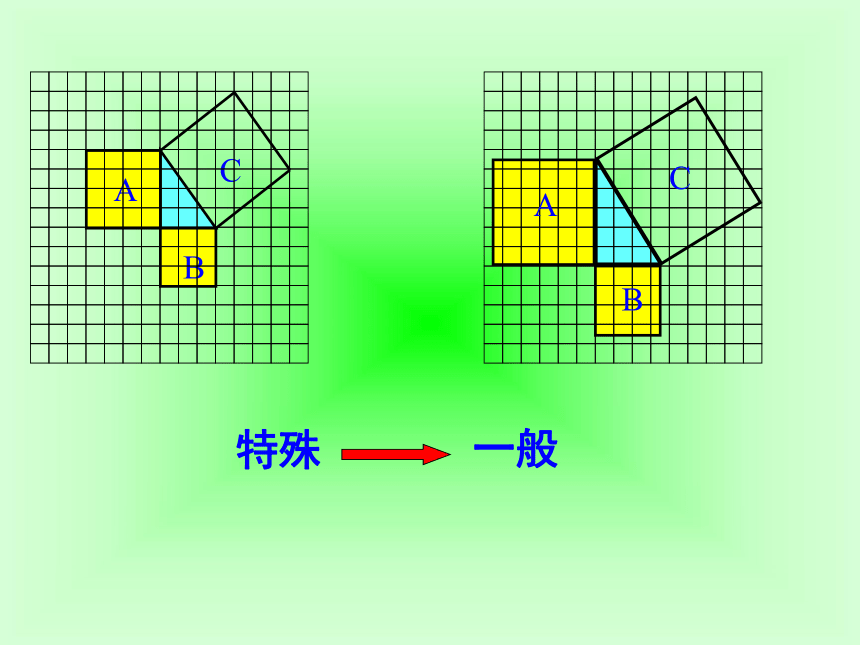
课件16张PPT。勾股定理的证明人教版 八年级数学(下册)ABC猜想:如果直角三角形两直角边分别为a、b,
斜边为c,那么ABC特殊一般通过拼图利用面积法验证: 准备四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,斜边为c);思考:如何用这四个直角三角形拼出
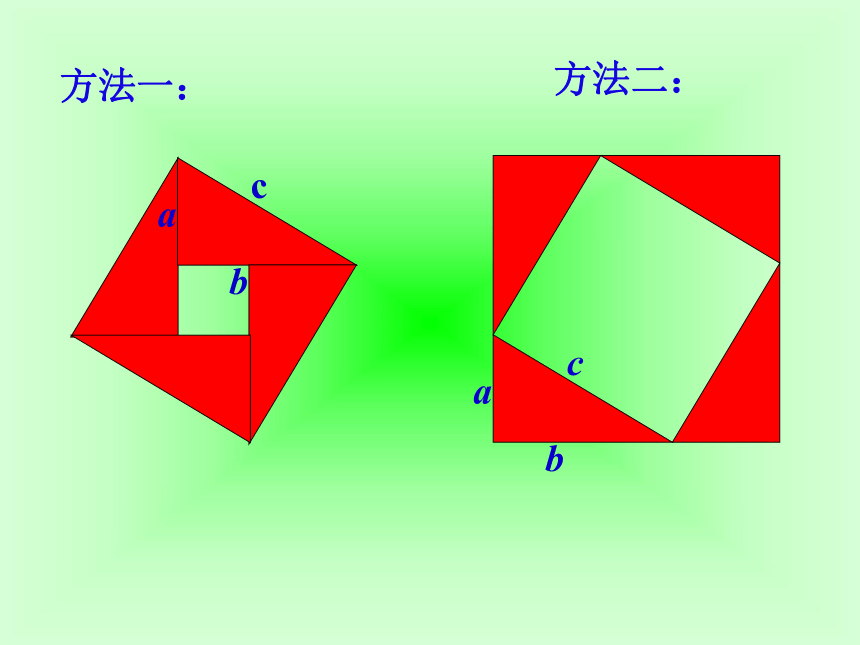
一个边长为c的正方形呢? 方法一:方法二:也可以表示为_________________大正方形的面积可以表示为____方法一:面积法证等式的步骤:
1、用不同的方法表示
同一个图形的面积;
2、利用面积相等列出
等式;
3、化简整理由面积相等可得:化简整理:也可以表示为_________________大正方形的面积可以表示为________面积法证等式的步骤:
1、用不同的方法表示
同一个图形的面积;
2、利用面积相等列出
等式;
3、化简整理由面积相等可得:化简整理:∴方法二:勾股定理:
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
即:直角三角形两直角边的平方和等于
斜边的平方。勾股弦 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955 两千多年前,古希腊的毕达哥拉斯学派发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。国家之一。早在三千多年前,国家之一。早在三千多年前,勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前, 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出 “勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,故称之为“赵爽弦图”赵爽弦图思考1:两个正方形的面积之和是多少?思考2:拼成的正方形的面积是多少?赵爽的智慧“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲。因此,当 2002年国际数学家大会在北京召开时, “赵爽弦图”被选作大会会徽。abc 1876年,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的证法,这一证法在数学史上被传为佳话。
后来伽菲尔德就任美国第二十任总统,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法” 。
总统证法((123( 勾股定理是几何学中的明珠,它充满了无穷的魅力,千百年来,吸引了众多的数学爱好者研究它的证明方法,上至帝王总统,下至平民百姓。有资料表明,关于勾股定理的证明方法已有500余种。谢谢!
斜边为c,那么ABC特殊一般通过拼图利用面积法验证: 准备四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,斜边为c);思考:如何用这四个直角三角形拼出
一个边长为c的正方形呢? 方法一:方法二:也可以表示为_________________大正方形的面积可以表示为____方法一:面积法证等式的步骤:
1、用不同的方法表示
同一个图形的面积;
2、利用面积相等列出
等式;
3、化简整理由面积相等可得:化简整理:也可以表示为_________________大正方形的面积可以表示为________面积法证等式的步骤:
1、用不同的方法表示
同一个图形的面积;
2、利用面积相等列出
等式;
3、化简整理由面积相等可得:化简整理:∴方法二:勾股定理:
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
即:直角三角形两直角边的平方和等于
斜边的平方。勾股弦 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955 两千多年前,古希腊的毕达哥拉斯学派发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。国家之一。早在三千多年前,国家之一。早在三千多年前,勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前, 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出 “勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,故称之为“赵爽弦图”赵爽弦图思考1:两个正方形的面积之和是多少?思考2:拼成的正方形的面积是多少?赵爽的智慧“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲。因此,当 2002年国际数学家大会在北京召开时, “赵爽弦图”被选作大会会徽。abc 1876年,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的证法,这一证法在数学史上被传为佳话。
后来伽菲尔德就任美国第二十任总统,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法” 。
总统证法((123( 勾股定理是几何学中的明珠,它充满了无穷的魅力,千百年来,吸引了众多的数学爱好者研究它的证明方法,上至帝王总统,下至平民百姓。有资料表明,关于勾股定理的证明方法已有500余种。谢谢!
