北师大版九年级数学下册第三章3.4圆周角和圆心角的关系 课件
文档属性
| 名称 | 北师大版九年级数学下册第三章3.4圆周角和圆心角的关系 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 480.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-14 11:32:41 | ||
图片预览


文档简介
课件32张PPT。第三章 圆3.4 圆周角和圆心角的关系
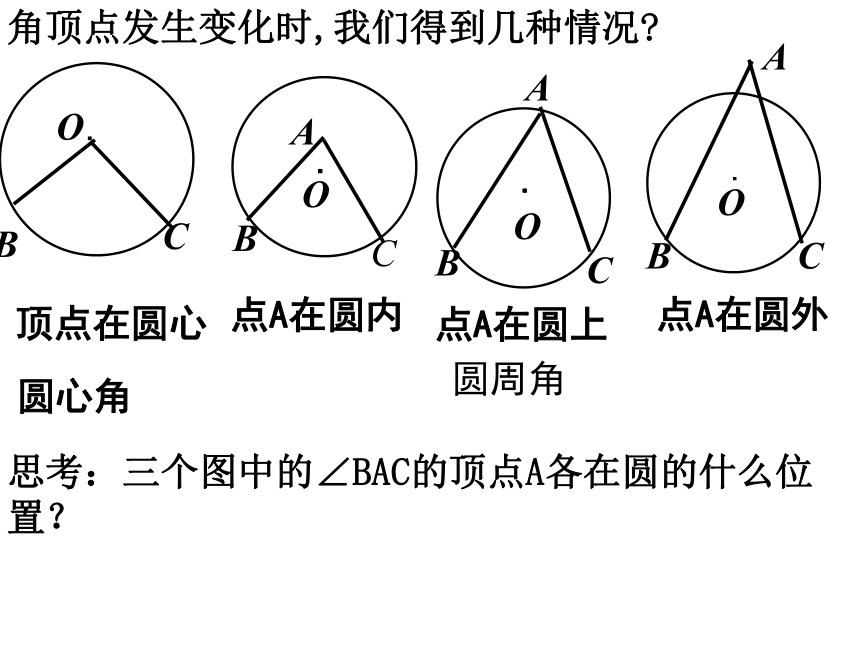
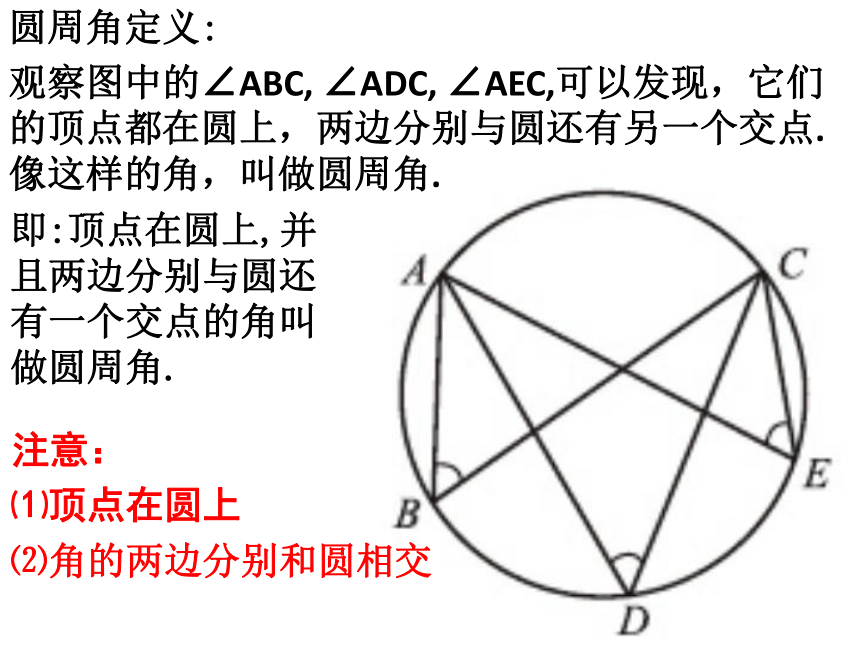
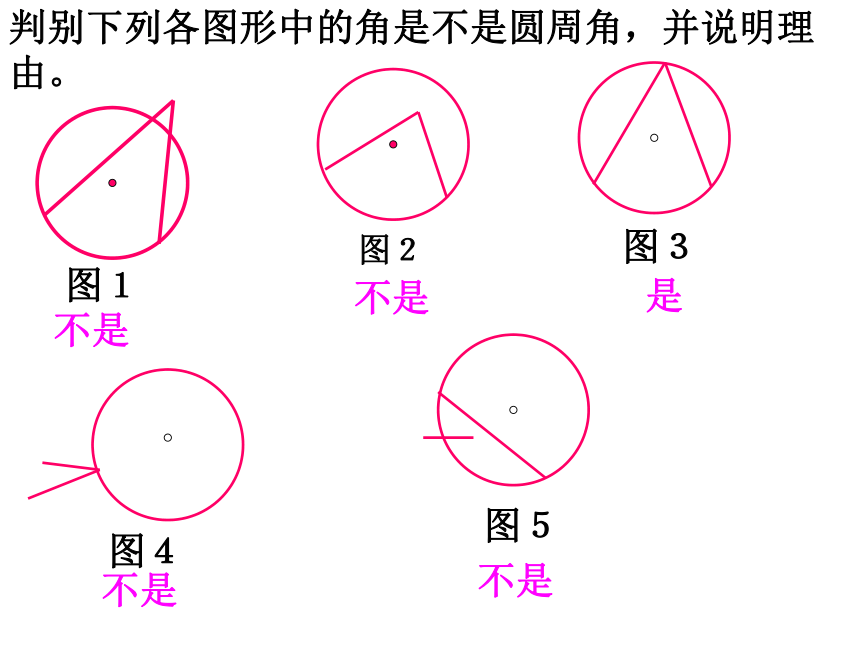
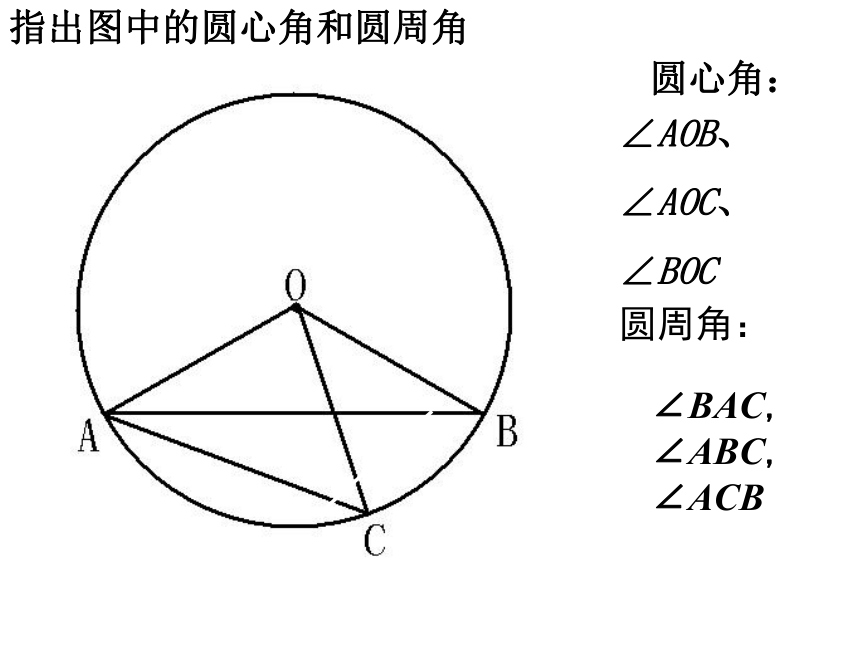
(第1课时) 1.圆心角的定义?顶点在圆心的角叫圆心角2.圆心角的度数和它所对的弧的度数有何关系?如图:∠AOB 弧AB的度数3.在同圆或等圆中,如果两个圆心角、两条 、两条 中有一组量相等,那么它们所对应的其余各组量都分别相等。弧弦=角顶点发生变化时,我们得到几种情况?思考:三个图中的∠BAC的顶点A各在圆的什么位置? 圆周角点A在圆内点A在圆外点A在圆上顶点在圆心圆心角圆周角定义: 观察图中的∠ABC, ∠ADC, ∠AEC,可以发现,它们的顶点都在圆上,两边分别与圆还有另一个交点.像这样的角,叫做圆周角.即:顶点在圆上,并且两边分别与圆还有一个交点的角叫做圆周角.注意:⑴顶点在圆上⑵角的两边分别和圆相交判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是图1图2图3图4图5指出图中的圆心角和圆周角圆周角:∠AOB、
∠AOC、
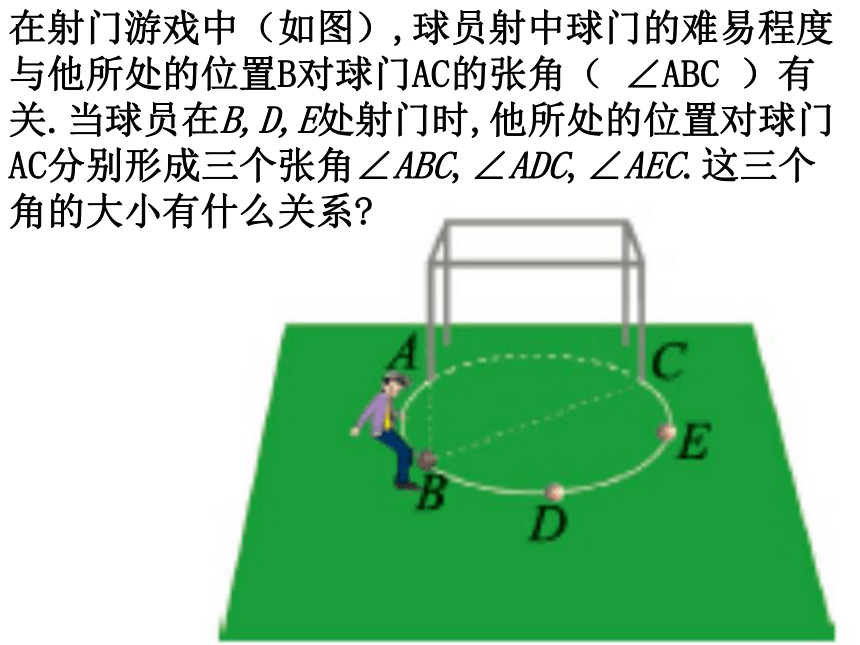
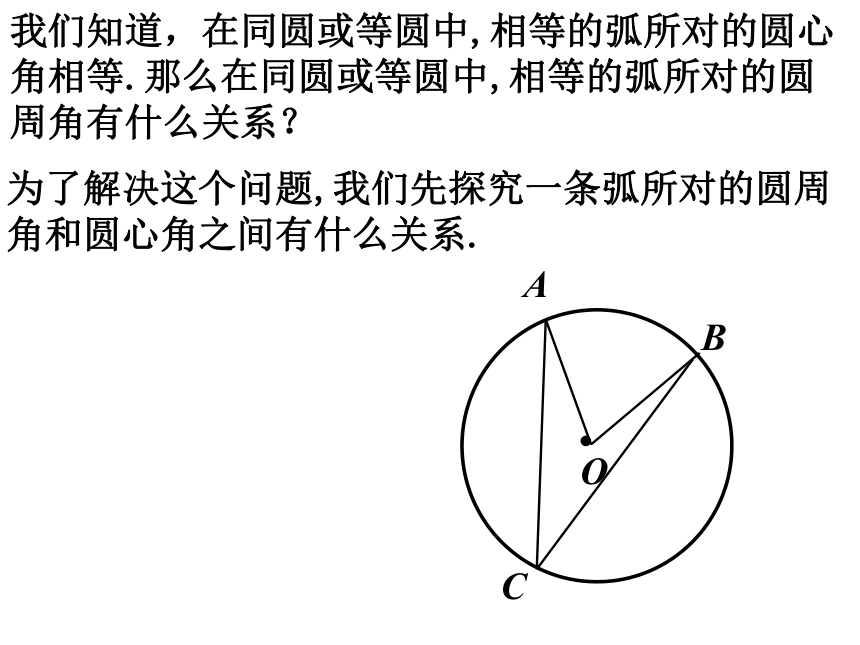
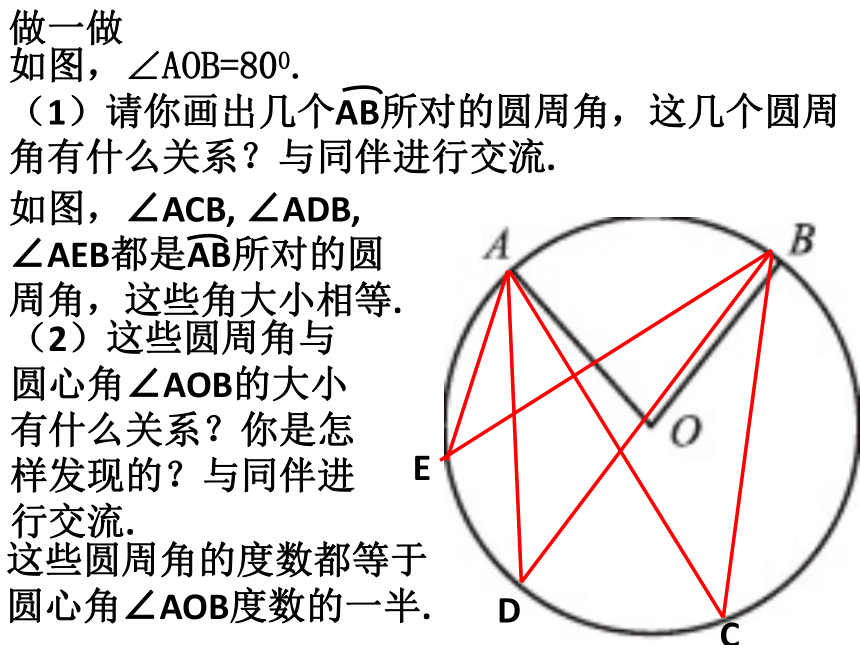
∠BOC∠BAC, ∠ABC, ∠ACB圆心角:在射门游戏中(如图),球员射中球门的难易程度与他所处的位置B对球门AC的张角( ∠ABC )有关.当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角的大小有什么关系?为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有什么关系.我们知道,在同圆或等圆中,相等的弧所对的圆心角相等.那么在同圆或等圆中,相等的弧所对的圆周角有什么关系?做一做如图,∠AOB=800.(2)这些圆周角与圆心角∠AOB的大小有什么关系?你是怎样发现的?与同伴进行交流.这些圆周角的度数都等于圆心角∠AOB度数的一半.议一议在上图中,改变∠AOB的度数,你得到的结论还成立吗?仍然成立.圆周角定理
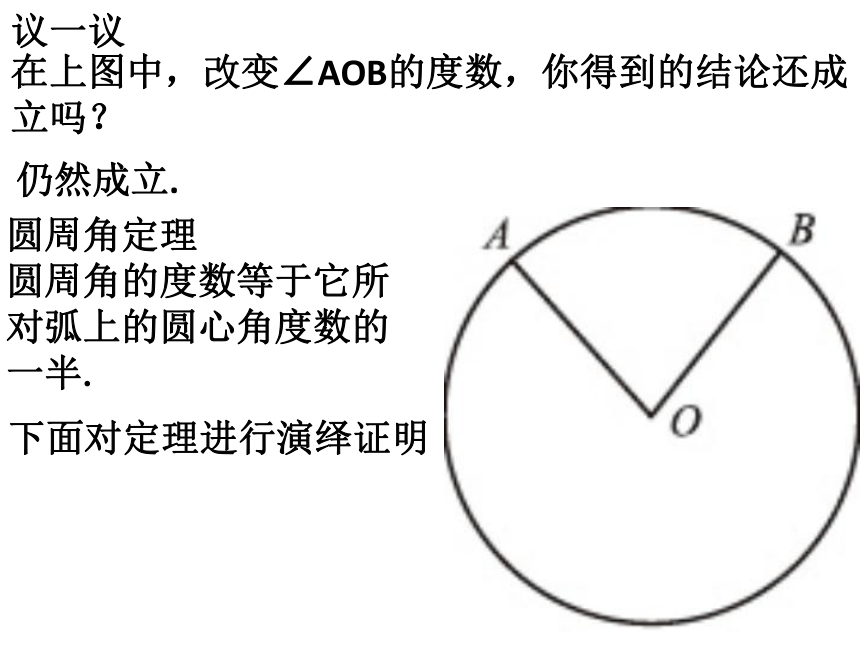
圆周角的度数等于它所对弧上的圆心角度数的一半.下面对定理进行演绎证明圆周角定理
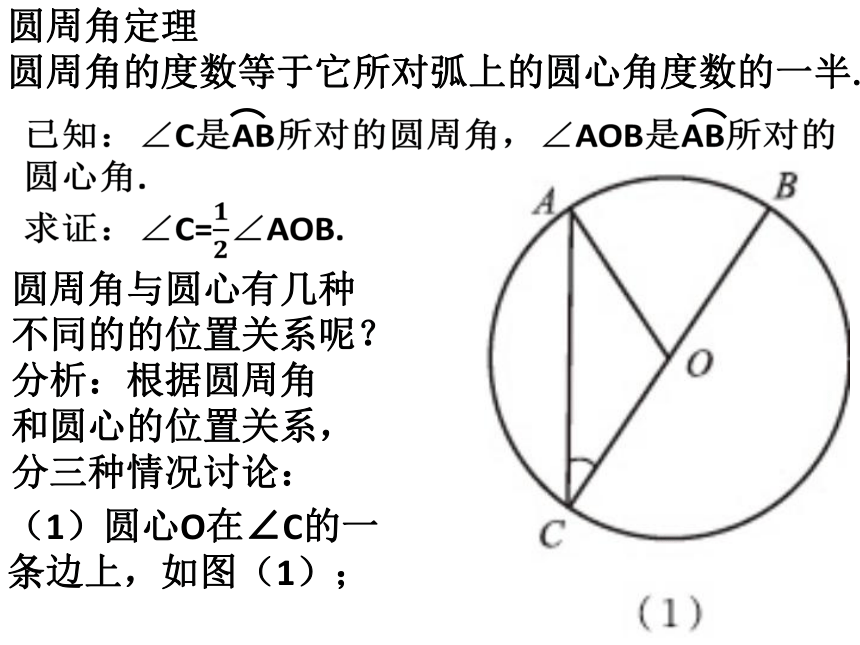
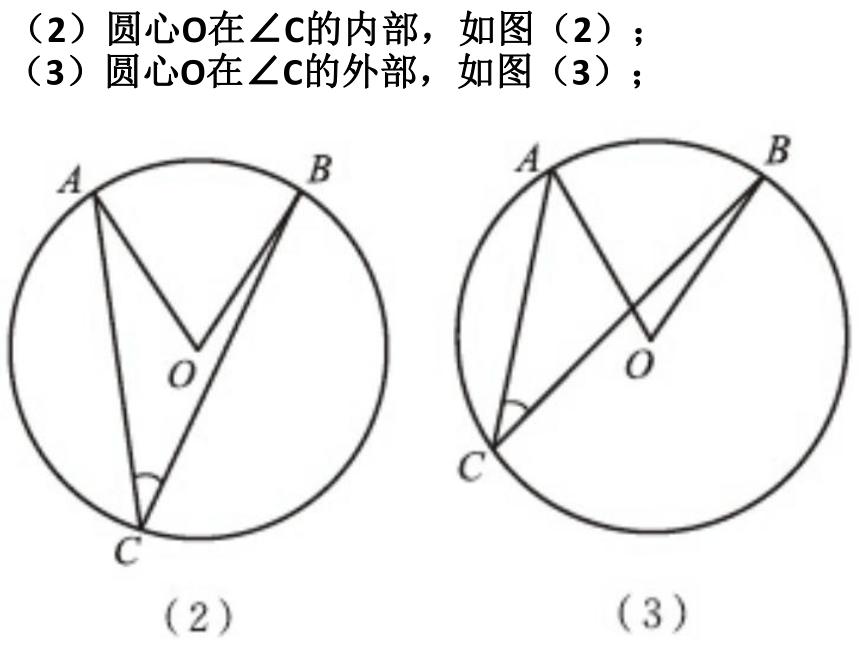
圆周角的度数等于它所对弧上的圆心角度数的一半.圆周角与圆心有几种不同的的位置关系呢?分析:根据圆周角和圆心的位置关系,分三种情况讨论:(1)圆心O在∠C的一条边上,如图(1);(2)圆心O在∠C的内部,如图(2);(3)圆心O在∠C的外部,如图(3);∵∠AOB是△ACO的外角,∴∠AOB=∠A+∠C.∵OA=OC,∴∠A=∠C.∴∠AOB=2∠C.在三种位置关系中,我们选择(1)给出证明,其他情况可以转化为(1)的情况进行证明.证明:(1)圆心O在∠C的一条边上,如图(1);请你完成图(2)和图(3)两种情况的证明.怎样才能转化为(1)的情况?过点C作直径CD.证明:(2)圆心O在∠C的内部,如图(2);D∵∠AOD是△ACO的外角,∴∠AOD=∠A+∠ACD.∵OA=OC,∴∠AOD=2∠ACD.过点C作直径CD.证明:(3)圆心O在∠C的外部,如图(3);怎样才能转化为(1)的情况?D∵∠AOD是△ACO的外角,∴∠AOD=∠A+∠ACD.∵OA=OC,∴∠AOD=2∠ACD.想一想在上图的射门游戏中,当球员在B,D,E处射门时,所形成三个张角∠ABC,∠ADC,∠AEC的大小有什么关系?你能用圆周角定理证明你的结论吗?推论 同弧或等弧所对的圆周角相等.如图,在⊙O中,∠O=50°,求∠A的度数.练习∠A=250.如图,哪个角与∠BAC相等,你还能找到那些相等的角?解:∠BAC=∠BDC
∠ADB=∠ACB
∠CAD=∠CBD
∠ABD=∠ACD如图,OA、OB、OC都是⊙O的半径,∠AOB=2 ∠BOC,∠ACB与∠BAC的大小有什么关系,为什么?解:∠ACB=2∠BAC.如图,A,B,C,D是⊙O上的四点,且∠C=100°,求∠BOD和∠A的度数.∠BOD=1600, ∠A=800.为什么有些电影院的座位排列(横排)呈圆弧形?说一说这设计的合理性。答:有些电影院的坐位排列呈圆弧形,这样设计的理由是尽量保证同排的观众视角相等。船在航行过程中,船长常常通过测定角度来确定是否遇到暗礁,如图,A,B表示灯塔,暗礁分布在经过A、B两点的一个圆形区域内,优弧AB上任一点C都是有触礁危险的临界点,∠ACB就是“危险角”.当船P位于安全区域时,它与两个灯塔的夹角∠α与“危险角”有怎样的大小关系?解:当船位于安全区域时,即船位于暗礁区域外(即⊙O外) ,与两个灯塔的夹角∠α小于“危险角” 。提示:设AP与⊙O交于点E,连接BE,则∠AEB就是“危险角” 。E如图,在直径为AB的半圆中,O为圆心,C,D为半圆上的两点,∠COD=50°,则∠CAD=_______.25o判断
(1)顶点在圆上的角叫圆周角.( )
(2)圆周角的度数等于所对弧的度数的一半.( ) ×√半径为R的圆中,有一弦分圆周成1:4两部分,则弦所对的圆周角的度数是_______________.36o或144°如图,△ABC是⊙O的内接三角形,若∠ABC =70°则∠AOC的度数等于( )
A.140° B.130°
C.120° D.110°答案:A 如图,已知AB为⊙O的直径,点C在⊙上,∠C=15°,则∠BOC的度数为( )
A.15° B. 30°
C. 45° D.60° 答案:B 如图,点B,C在⊙O上,且BO=BC,则圆周角∠BAC等于( )答案:D A.60°B.50°C.40°D.30°如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
A.30° B.40° C.50° D.60°答案:A【规律方法】解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理.一 、这节课主要学习了两个知识点:
1、圆周角定义。
2、圆周角定理及其定理应用。
二、方法上主要学习了圆周角定理的证明,渗透了类比,“特殊到一般”的思想方法和分类讨论的思想方法。
三、圆周角及圆周角定理的应用极其广泛,也是中考的一个重要考点,望同学们灵活运用。小结:学完本课后你有哪些收获?作业:
习题3.4 1、2、3、4题。
(第1课时) 1.圆心角的定义?顶点在圆心的角叫圆心角2.圆心角的度数和它所对的弧的度数有何关系?如图:∠AOB 弧AB的度数3.在同圆或等圆中,如果两个圆心角、两条 、两条 中有一组量相等,那么它们所对应的其余各组量都分别相等。弧弦=角顶点发生变化时,我们得到几种情况?思考:三个图中的∠BAC的顶点A各在圆的什么位置? 圆周角点A在圆内点A在圆外点A在圆上顶点在圆心圆心角圆周角定义: 观察图中的∠ABC, ∠ADC, ∠AEC,可以发现,它们的顶点都在圆上,两边分别与圆还有另一个交点.像这样的角,叫做圆周角.即:顶点在圆上,并且两边分别与圆还有一个交点的角叫做圆周角.注意:⑴顶点在圆上⑵角的两边分别和圆相交判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是图1图2图3图4图5指出图中的圆心角和圆周角圆周角:∠AOB、
∠AOC、
∠BOC∠BAC, ∠ABC, ∠ACB圆心角:在射门游戏中(如图),球员射中球门的难易程度与他所处的位置B对球门AC的张角( ∠ABC )有关.当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角的大小有什么关系?为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有什么关系.我们知道,在同圆或等圆中,相等的弧所对的圆心角相等.那么在同圆或等圆中,相等的弧所对的圆周角有什么关系?做一做如图,∠AOB=800.(2)这些圆周角与圆心角∠AOB的大小有什么关系?你是怎样发现的?与同伴进行交流.这些圆周角的度数都等于圆心角∠AOB度数的一半.议一议在上图中,改变∠AOB的度数,你得到的结论还成立吗?仍然成立.圆周角定理
圆周角的度数等于它所对弧上的圆心角度数的一半.下面对定理进行演绎证明圆周角定理
圆周角的度数等于它所对弧上的圆心角度数的一半.圆周角与圆心有几种不同的的位置关系呢?分析:根据圆周角和圆心的位置关系,分三种情况讨论:(1)圆心O在∠C的一条边上,如图(1);(2)圆心O在∠C的内部,如图(2);(3)圆心O在∠C的外部,如图(3);∵∠AOB是△ACO的外角,∴∠AOB=∠A+∠C.∵OA=OC,∴∠A=∠C.∴∠AOB=2∠C.在三种位置关系中,我们选择(1)给出证明,其他情况可以转化为(1)的情况进行证明.证明:(1)圆心O在∠C的一条边上,如图(1);请你完成图(2)和图(3)两种情况的证明.怎样才能转化为(1)的情况?过点C作直径CD.证明:(2)圆心O在∠C的内部,如图(2);D∵∠AOD是△ACO的外角,∴∠AOD=∠A+∠ACD.∵OA=OC,∴∠AOD=2∠ACD.过点C作直径CD.证明:(3)圆心O在∠C的外部,如图(3);怎样才能转化为(1)的情况?D∵∠AOD是△ACO的外角,∴∠AOD=∠A+∠ACD.∵OA=OC,∴∠AOD=2∠ACD.想一想在上图的射门游戏中,当球员在B,D,E处射门时,所形成三个张角∠ABC,∠ADC,∠AEC的大小有什么关系?你能用圆周角定理证明你的结论吗?推论 同弧或等弧所对的圆周角相等.如图,在⊙O中,∠O=50°,求∠A的度数.练习∠A=250.如图,哪个角与∠BAC相等,你还能找到那些相等的角?解:∠BAC=∠BDC
∠ADB=∠ACB
∠CAD=∠CBD
∠ABD=∠ACD如图,OA、OB、OC都是⊙O的半径,∠AOB=2 ∠BOC,∠ACB与∠BAC的大小有什么关系,为什么?解:∠ACB=2∠BAC.如图,A,B,C,D是⊙O上的四点,且∠C=100°,求∠BOD和∠A的度数.∠BOD=1600, ∠A=800.为什么有些电影院的座位排列(横排)呈圆弧形?说一说这设计的合理性。答:有些电影院的坐位排列呈圆弧形,这样设计的理由是尽量保证同排的观众视角相等。船在航行过程中,船长常常通过测定角度来确定是否遇到暗礁,如图,A,B表示灯塔,暗礁分布在经过A、B两点的一个圆形区域内,优弧AB上任一点C都是有触礁危险的临界点,∠ACB就是“危险角”.当船P位于安全区域时,它与两个灯塔的夹角∠α与“危险角”有怎样的大小关系?解:当船位于安全区域时,即船位于暗礁区域外(即⊙O外) ,与两个灯塔的夹角∠α小于“危险角” 。提示:设AP与⊙O交于点E,连接BE,则∠AEB就是“危险角” 。E如图,在直径为AB的半圆中,O为圆心,C,D为半圆上的两点,∠COD=50°,则∠CAD=_______.25o判断
(1)顶点在圆上的角叫圆周角.( )
(2)圆周角的度数等于所对弧的度数的一半.( ) ×√半径为R的圆中,有一弦分圆周成1:4两部分,则弦所对的圆周角的度数是_______________.36o或144°如图,△ABC是⊙O的内接三角形,若∠ABC =70°则∠AOC的度数等于( )
A.140° B.130°
C.120° D.110°答案:A 如图,已知AB为⊙O的直径,点C在⊙上,∠C=15°,则∠BOC的度数为( )
A.15° B. 30°
C. 45° D.60° 答案:B 如图,点B,C在⊙O上,且BO=BC,则圆周角∠BAC等于( )答案:D A.60°B.50°C.40°D.30°如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
A.30° B.40° C.50° D.60°答案:A【规律方法】解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理.一 、这节课主要学习了两个知识点:
1、圆周角定义。
2、圆周角定理及其定理应用。
二、方法上主要学习了圆周角定理的证明,渗透了类比,“特殊到一般”的思想方法和分类讨论的思想方法。
三、圆周角及圆周角定理的应用极其广泛,也是中考的一个重要考点,望同学们灵活运用。小结:学完本课后你有哪些收获?作业:
习题3.4 1、2、3、4题。
