北师大版七年级上册第二章2.5有理数的减法 课件
文档属性
| 名称 | 北师大版七年级上册第二章2.5有理数的减法 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 462.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-14 00:00:00 | ||
图片预览






文档简介
课件17张PPT。第二章 有理数及其运算
第5节 有理数的减法 绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.(3) 一个数与0相加,仍得这个数.
复习计算(1) 1 + 6 =
(2)(–2)+(–8) =
(3) (–9)+ 10 =
(4) 5 + (–9) =
(5) (–2.2)+ 2.2 =
(6) 6 + 0 =
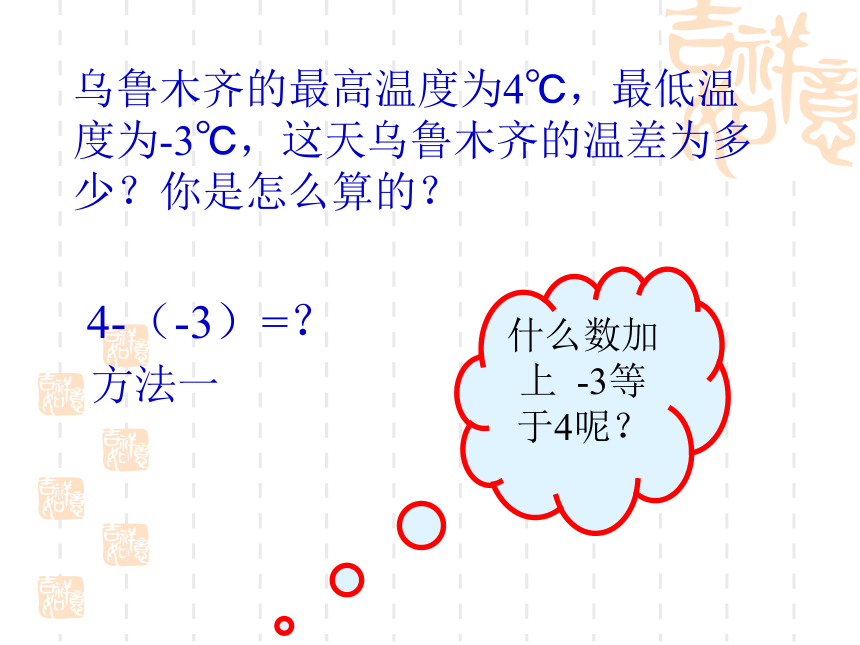
(7) 0 + (–8) =7–101–46–8 同号两数相加,取相同的符号,并把绝对值相加.0乌鲁木齐的最高温度为4℃,最低温度为-3℃,这天乌鲁木齐的温差为多少?你是怎么算的?4-(-3)=?什么数加上 -3等于4呢?
方法一方法二合作探究计算下列各式:
15 – 6 = 15+(-6)=
19 – 3= 19+(-3)=
12 – 0= 12+ 0=
8 -(-3)= 8+3=
10 -(-3)= 10+3=991616121211111313你能得到什么结论?有理数减法法则减去一个数,等于加上这个数的相反数注意:减法在运算时有 2 个要素要发生变化。1 减 加
2 减数 相反数 a–b=a+(–b)1. 下列括号内各应填什么数?
(1)(-2)-(-3)=(-2)+( );
(2) 0 - (-4)= 0 +( );
(3)(-6)- 3 =(-6)+( );
(4) 1-(+39)= 1 +( )
试一试34- 3- 39例1 计算下列各题:
(1)9 -(- 5) (2) (- 3)- 1
(3)0 - 8 (4)(- 5)- 0(2)原式=( -3)+(- 1)
= - 4解:(1)原式= 9+5
=14(3)原式 = 0+ (- 8)= - 8(4)原式 = -5我最行!口算:(看谁算得快)
(1)3 – 5 ; (2)3 – ( – 5);
(3) – 3 – 5; (4)( – 3) – (- 5);
(5)–6 –( –6); (6) – 7 – 0;
(7)0 – ( –7) ; (8 ) – 6 – 6
例2 世界上最高的山峰是珠穆朗玛峰, 其海拔高度是 8844 米,吐鲁番盆地的海拔高度是 –155 米,两处高度相差多少米?解:8844-(-155)
=8844+155
=8999(米)
答:两处高度相差8999米。例2世界上最高的山峰是珠穆朗玛峰,其海拔高度大约是8 848米,吐鲁番盆地的海拔高度大约是-155米.两处高度相差多少米?
8 848米有多少层楼高?解:8 848-(-155)=8 848+155=9 003(米)
答:两处高度相差9003米。例3:
全班学生分为五个组进行游戏,每组的基本分
为100分,答对一题加50分,答错一题扣50分
游戏结束时,各组的分数如下:(1)第一名超出第二名多少分?解:由上表可以看出,第一名得了350分,第二名得了150分。350 – 150=200(分)
答:第一名超出第二名200分第一名超出第五名多少分?350 - (- 400)=750(分)
答:第一名超出第五名750分一、填空题
1、有理数的减法法则是:减去一个数等于加上这个的 。
2、①3.6-4.7= ②(-7)-12=
③(+13)-(-7)= ④5-(-3)=
⑤0-15= ⑥0-(-8)=
⑦(-3.4)-0= ⑧(-1.24)-5.73=
⑨(-4)-(-4.375)= ⑩2-(+5)=
3、(1)(-5)+( )= -8;
(-3)+( )=2达标测试(2)比2°C低8°C的温度是 ;
比-3°C低6°C的温度 ;
(3)比0小4的数是 ;
比0 小-4的数是______________
(4)7.4比8.3小 ;
7.4比8.3大 。
4、若m>0,n<0,则m-n 0;
若m<0,n>0, 则m-n 0。二、选择题
1、下面等式正确的是( )
A、a-b=(-a)+ b B、a-(-b)=(-a)+(-b)
C、(-a)-(-b)=(-a)+(-b) D、a-(-b)=a+b
2、下列说法中下正确的是( )
A.两个数的差一定小于被减数
B、若两个数的差为0,则这两数必相等
C、零减去一个数一定得负数
D、一个负数减去一个负数结果仍是负数
3、设两个有理数的和为a,这两个有理数的差为b,则a、b的大小关系是( )
A、a=b B、 a C、a>b D、不能确定课堂小结
今天我们从实例出发,经过比较,归纳得出了有理数减法法则,并通过推理说明了法则的合理性。这样有理数的减法只需将减数变成它的相反数,把减法转化为加法(注意被减数是永远不变的)。从而有理数的加法和减法这两种互逆的运算可用加法统一起来。想一想还有什么运算与这种情形类似?这说明在一定的条件下,矛盾的双方可以向其对立面转化。同学们,再见!
第5节 有理数的减法 绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.(3) 一个数与0相加,仍得这个数.
复习计算(1) 1 + 6 =
(2)(–2)+(–8) =
(3) (–9)+ 10 =
(4) 5 + (–9) =
(5) (–2.2)+ 2.2 =
(6) 6 + 0 =
(7) 0 + (–8) =7–101–46–8 同号两数相加,取相同的符号,并把绝对值相加.0乌鲁木齐的最高温度为4℃,最低温度为-3℃,这天乌鲁木齐的温差为多少?你是怎么算的?4-(-3)=?什么数加上 -3等于4呢?
方法一方法二合作探究计算下列各式:
15 – 6 = 15+(-6)=
19 – 3= 19+(-3)=
12 – 0= 12+ 0=
8 -(-3)= 8+3=
10 -(-3)= 10+3=991616121211111313你能得到什么结论?有理数减法法则减去一个数,等于加上这个数的相反数注意:减法在运算时有 2 个要素要发生变化。1 减 加
2 减数 相反数 a–b=a+(–b)1. 下列括号内各应填什么数?
(1)(-2)-(-3)=(-2)+( );
(2) 0 - (-4)= 0 +( );
(3)(-6)- 3 =(-6)+( );
(4) 1-(+39)= 1 +( )
试一试34- 3- 39例1 计算下列各题:
(1)9 -(- 5) (2) (- 3)- 1
(3)0 - 8 (4)(- 5)- 0(2)原式=( -3)+(- 1)
= - 4解:(1)原式= 9+5
=14(3)原式 = 0+ (- 8)= - 8(4)原式 = -5我最行!口算:(看谁算得快)
(1)3 – 5 ; (2)3 – ( – 5);
(3) – 3 – 5; (4)( – 3) – (- 5);
(5)–6 –( –6); (6) – 7 – 0;
(7)0 – ( –7) ; (8 ) – 6 – 6
例2 世界上最高的山峰是珠穆朗玛峰, 其海拔高度是 8844 米,吐鲁番盆地的海拔高度是 –155 米,两处高度相差多少米?解:8844-(-155)
=8844+155
=8999(米)
答:两处高度相差8999米。例2世界上最高的山峰是珠穆朗玛峰,其海拔高度大约是8 848米,吐鲁番盆地的海拔高度大约是-155米.两处高度相差多少米?
8 848米有多少层楼高?解:8 848-(-155)=8 848+155=9 003(米)
答:两处高度相差9003米。例3:
全班学生分为五个组进行游戏,每组的基本分
为100分,答对一题加50分,答错一题扣50分
游戏结束时,各组的分数如下:(1)第一名超出第二名多少分?解:由上表可以看出,第一名得了350分,第二名得了150分。350 – 150=200(分)
答:第一名超出第二名200分第一名超出第五名多少分?350 - (- 400)=750(分)
答:第一名超出第五名750分一、填空题
1、有理数的减法法则是:减去一个数等于加上这个的 。
2、①3.6-4.7= ②(-7)-12=
③(+13)-(-7)= ④5-(-3)=
⑤0-15= ⑥0-(-8)=
⑦(-3.4)-0= ⑧(-1.24)-5.73=
⑨(-4)-(-4.375)= ⑩2-(+5)=
3、(1)(-5)+( )= -8;
(-3)+( )=2达标测试(2)比2°C低8°C的温度是 ;
比-3°C低6°C的温度 ;
(3)比0小4的数是 ;
比0 小-4的数是______________
(4)7.4比8.3小 ;
7.4比8.3大 。
4、若m>0,n<0,则m-n 0;
若m<0,n>0, 则m-n 0。二、选择题
1、下面等式正确的是( )
A、a-b=(-a)+ b B、a-(-b)=(-a)+(-b)
C、(-a)-(-b)=(-a)+(-b) D、a-(-b)=a+b
2、下列说法中下正确的是( )
A.两个数的差一定小于被减数
B、若两个数的差为0,则这两数必相等
C、零减去一个数一定得负数
D、一个负数减去一个负数结果仍是负数
3、设两个有理数的和为a,这两个有理数的差为b,则a、b的大小关系是( )
A、a=b B、 a C、a>b D、不能确定课堂小结
今天我们从实例出发,经过比较,归纳得出了有理数减法法则,并通过推理说明了法则的合理性。这样有理数的减法只需将减数变成它的相反数,把减法转化为加法(注意被减数是永远不变的)。从而有理数的加法和减法这两种互逆的运算可用加法统一起来。想一想还有什么运算与这种情形类似?这说明在一定的条件下,矛盾的双方可以向其对立面转化。同学们,再见!
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
