2016--2017学年度第一学期北师版数学八年级单元检测题第三章《位置与坐标》A
文档属性
| 名称 | 2016--2017学年度第一学期北师版数学八年级单元检测题第三章《位置与坐标》A |  | |
| 格式 | zip | ||
| 文件大小 | 287.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-14 06:55:18 | ||
图片预览




文档简介
2016--2017学年度第一学期北师版数学八年级单元检测题
第三章《位置与坐标》A
一.选择题(共12小题)
1.(2015?北京)如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,﹣1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( ) 21*cnjy*com
A.景仁宫(4,2)? B.养心殿(﹣2,3)
C.保和殿(1,0) D.武英殿(﹣3.5,﹣4)
2.(2016?大连)在平面直角坐标系中,点(1,5)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.(2016?临夏州)已知点P(0,m)在y轴的负半轴上,则点M(﹣m,﹣m+1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(2016?柳州)如图,在平面直角坐标系中,点P的坐标为( )
A.(3,﹣2) B.(﹣2,3) C.(﹣3,2) D.(2,﹣3)
5.(2016?滨州)如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是( )
A.(2,﹣3) B.(2,3) C.(3,2) D.(3,﹣2)
6.(2016?成都)平面直角坐标系中,点P(﹣2,3)关于x轴对称的点的坐标为( )
A.(﹣2,﹣3) B.(2,﹣3) C.(﹣3,﹣2) D.(3,﹣2)
7.(2016?赤峰)平面直角坐标系内的点A(﹣1,2)与点B(﹣1,﹣2)关于( )
A.y轴对称 B.x轴对称 C.原点对称 D.直线y=x对称
8.(2016?武汉)已知点A(a,1)与点A′(5,b)关于坐标原点对称,则实数a、b的值是( )
A.a=5,b=1 B.a=﹣5,b=1 C.a=5,b=﹣1 D.a=﹣5,b=﹣1
9.(2015?贵港)在平面直角坐标系中,若点P(m,m﹣n)与点Q(﹣2,3)关于原点对称,则点M(m,n)在( )2-1-c-n-j-y
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.(2015?凉山州)在平面直角坐标系中,点P(﹣3,2)关于直线y=x对称点的坐标是( )
A.(﹣3,﹣2) B.(3,2) C.(2,﹣3) D.(3,﹣2)
11.(2016?安顺)如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )【出处:21教育名师】
A.(﹣2,﹣4) B.(﹣2,4) C.(2,﹣3) D.(﹣1,﹣3)
12.(2016?台湾)如图为A、B、C三点在坐标平面上的位置图.若A、B、C的x坐标的数字总和为a,y坐标的数字总和为b,则a﹣b之值为何?( )21教育名师原创作品
A.5 B.3 C.﹣3 D.﹣5
二.填空题(共6小题)
13.(2015?六盘水)观察中国象棋的棋盘,其中红方“马”的位置可以用一个数对(3,5)来表示,红“马”走完“马3进四”后到达B点,则表示B点位置的数对是: .21*cnjy*com
14.(2015?南京)在平面直角坐标系中,点A的坐标是(2,﹣3),作点A关于x轴的对称点,得到点A′,再作点A′关于y轴的对称点,得到点A″,则点A″的坐标是( , ).
15.(2016?黔南州)在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:
①△(a,b)=(﹣a,b);
②○(a,b)=(﹣a,﹣b);
③Ω(a,b)=(a,﹣b),
按照以上变换例如:△(○(1,2))=(1,﹣2),则○(Ω(3,4))等于 .
16.(2016?宜宾)在平面直角坐标系内,以点P(1,1)为圆心、为半径作圆,则该圆与y轴的交点坐标是 .
17.(2011?盐城)如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(﹣1,4).将△ABC沿y轴翻折到第一象限,则点C的对应点C′的坐标是 .
18.(2015?广元)若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是 .
三.解答题(共7小题)
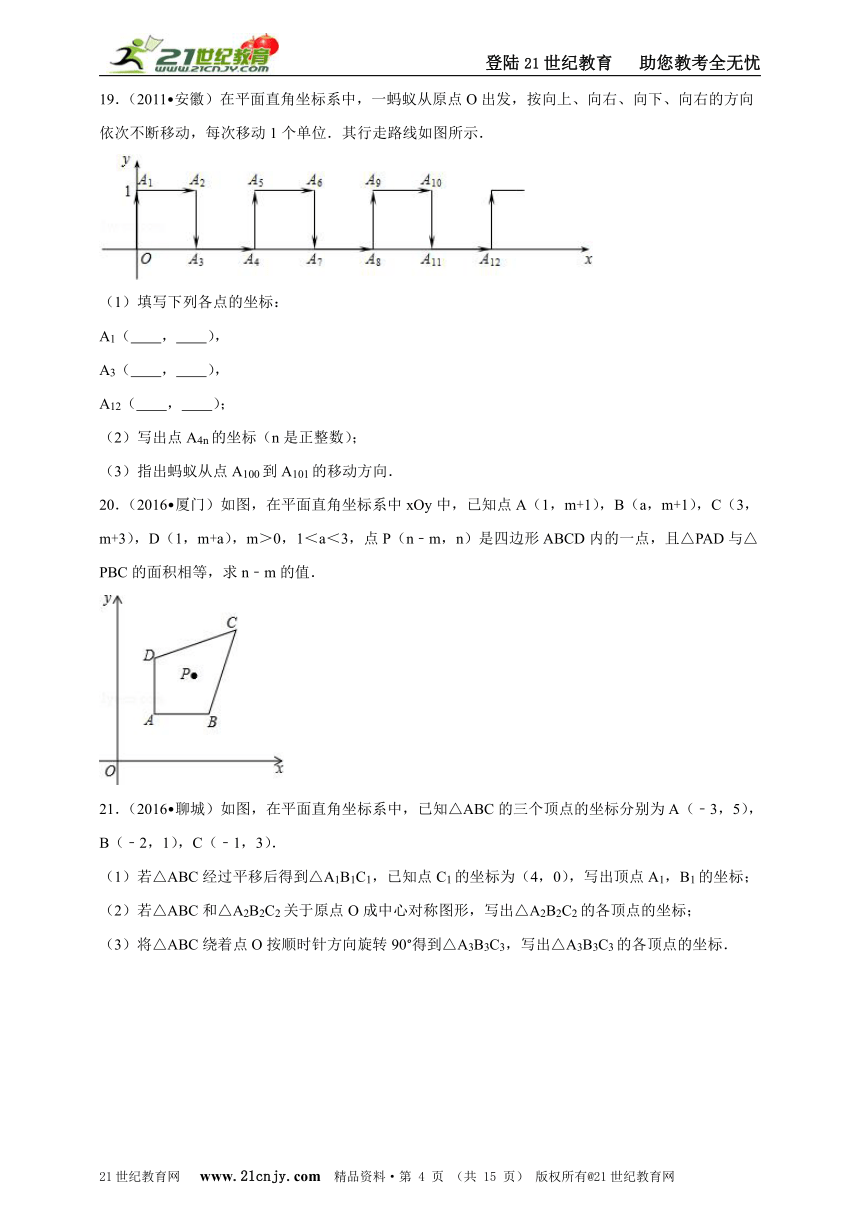
19.(2011?安徽)在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图所示.
(1)填写下列各点的坐标:
A1( , ),
A3( , ),
A12( , );
(2)写出点A4n的坐标(n是正整数);
(3)指出蚂蚁从点A100到A101的移动方向.
20.(2016?厦门)如图,在平面直角坐标系中xOy中,已知点A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),m>0,1<a<3,点P(n﹣m,n)是四边形ABCD内的一点,且△PAD与△PBC的面积相等,求n﹣m的值.
21.(2016?聊城)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
22.(2012?大庆)在直角坐标系中,C(2,3),C′(﹣4,3),C″(2,1),D(﹣4,1),A(0,a),B(a,O)(a>0).
(1)结合坐标系用坐标填空.
点C与C′关于点 对称; 点C与C″关于点 对称;点C与D关于点 对称;
(2)设点C关于点(4,2)的对称点是点P,若△PAB的面积等于5,求a值.
23.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点Q的坐标为(1,5),直线PQ∥y轴;
(4)点P到x轴、y轴的距离相等.
24.如图,在直角坐标系中,A(﹣1,5),B(﹣3,0),C(﹣4,3).
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1.
(2)写出点C1的坐标.
25.已知,如图,点A(a,b),B(c,d)在平面直角坐标系中的任意两点,且AC⊥x轴于点C,BD⊥x轴于点D.
(1)CD= ,|DB﹣AC|= ;(用含a,b,c,d的代数式表示)
(2)请猜想:A,B两点之间的距离 ;
(3)利用猜想,若A(﹣2,5),B(4,﹣4),求AB两点之间的距离.
答案与解析
一.选择题(共12小题)
1.【分析】根据平面直角坐标系,找出相应的位置,然后写出坐标即可.
【解答】解:根据表示太和门的点的坐标为(0,﹣1),表示九龙壁的点的坐标为(4,1),
可得:原点是中和殿,
所以可得景仁宫(2,4),养心殿(﹣2,3),保和殿(0,1),武英殿(﹣3.5,﹣3),
故选B
2.【分析】根据各象限内点的坐标特征解答即可.
【解答】解:点(1,5)所在的象限是第一象限.
故选A.
3.【分析】根据y轴的负半轴上点的横坐标等于零,纵坐标小于零,可得m的值,根据不等式的性质,可得到答案.
【解答】解:由点P(0,m)在y轴的负半轴上,得
m<0.
由不等式的性质,得
﹣m>0,﹣m+1>1,
则点M(﹣m,﹣m+1)在第一象限,
故选:A.
4.【分析】根据平面直角坐标系以及点的坐标的 定义写出即可.
【解答】解:点P的坐标为(3,﹣2).
故选A.
5.【分析】由题目中A点坐标特征推导得出平面直角坐标系y轴的位置,再通过C、D点坐标特征结合正五边形的轴对称性质就可以得出E点坐标了.21教育网
【解答】解:∵点A坐标为(0,a),
∴点A在该平面直角坐标系的y轴上,
∵点C、D的坐标为(b,m),(c,m),
∴点C、D关于y轴对称,
∵正五边形ABCDE是轴对称图形,
∴该平面直角坐标系经过点A的y轴是正五边形ABCDE的一条对称轴,
∴点B、E也关于y轴对称,
∵点B的坐标为(﹣3,2),
∴点E的坐标为(3,2).
故选:C.
6.【分析】直接利用关于x轴对称点的性质,横坐标不变,纵坐标互为相反数,进而得出答案.
【解答】解:点P(﹣2,3)关于x轴对称的点的坐标为(﹣2,﹣3).
故选:A.
7.【分析】根据关于x轴对称点的坐标特点:纵坐标互为相反数,横坐标不变可得答案.
【解答】解:平面直角坐标系内的点A(﹣1,2)与点B(﹣1,﹣2)关于x轴对称.
故选:B.
8.【分析】根据关于原点对称的点的横坐标与纵坐标都互为相反数解答.
【解答】解:∵点A(a,1)与点A′(5,b)关于坐标原点对称,
∴a=﹣5,b=﹣1.
故选D.
9.【分析】根据平面内两点关于原点对称的点,横坐标与纵坐标都互为相反数,则m=2且n=﹣3,从而得出点M(m,n)所在的象限.21cnjy.com
【解答】解:根据平面内两点关于原点对称的点,横坐标与纵坐标都互为相反数,
∴m=2且m﹣n=﹣3,
∴m=2,n=5
∴点M(m,n)在第一象限,
故选A.
10.【分析】根据直线y=x是第一、三象限的角平分线,和点P的坐标结合图形得到答案.
【解答】解:点P关于直线y=x对称点为点Q,
作AP∥x轴交y=x于A,
∵y=x是第一、三象限的角平分线,
∴点A的坐标为(2,2),
∵AP=AQ,
∴点Q的坐标为(2,﹣3)
故选:C.
11.【分析】直接利用平移中点的变化规律求解即可.
【解答】解:由题意可知此题规律是(x+2,y﹣3),照此规律计算可知顶点P(﹣4,﹣1)平移后的坐标是(﹣2,﹣4).2·1·c·n·j·y
故选A.
12.【分析】先求出A、B、C三点的横坐标的和为﹣1+0+5=4,纵坐标的和为﹣4﹣1+4=﹣1,再把它们相减即可求得a﹣b之值.www-2-1-cnjy-com
【解答】解:由图形可知:
a=﹣1+0+5=4,
b=﹣4﹣1+4=﹣1,
a﹣b=4+1=5.
故选:A.
二.填空题(共6小题)
13.【分析】根据图示,写出点B的位置的数对即可.
【解答】解:如图所示,
B点位置的数对是(4,7).
故答案为:(4,7).
14.【分析】分别利用x轴、y轴对称点的性质,得出A′,A″的坐标进而得出答案.
【解答】解:∵点A的坐标是(2,﹣3),作点A关于x轴的对称点,得到点A′,
∴A′的坐标为:(2,3),
∵点A′关于y轴的对称点,得到点A″,
∴点A″的坐标是:(﹣2,3).
故答案为:﹣2;3.
15.【分析】根据三种变换规律的特点解答即可.
【解答】解:○(Ω(3,4))=○(3,﹣4)=(﹣3,4).
故答案为:(﹣3,4).
16.【分析】在平面直角坐标系中,根据勾股定理先求出直角三角形的另外一个直角边,再根据点P的坐标即可得出答案.21·世纪*教育网
【解答】解:以(1,1)为圆心,为半径画圆,与y轴相交,构成直角三角形,
用勾股定理计算得另一直角边的长为2,
则与y轴交点坐标为(0,3)或(0,﹣1).
故答案为:(0,3),(0,﹣1).
17.【分析】由点A的坐标为(﹣1,4),即可求得点C的坐标,又由将△ABC沿y轴翻折到第一象限,即可得点C与C′关于y轴对称,则可求得点C′的坐标.【来源:21cnj*y.co*m】
【解答】解:如图:∵点A的坐标为(﹣1,4),
∴点C的坐标为(﹣3,1),
∵将△ABC沿y轴翻折到第一象限,
∴点C的对应点C′的坐标是(3,1).
故答案为:(3,1).
18.【分析】根据绝对值的意义和平方根得到x=±5,y=±2,再根据第二象限的点的坐标特点得到x<0,y>0,于是x=﹣5,y=2,然后可直接写出P点坐标.【版权所有:21教育】
【解答】解:∵|x|=3,y2=25,
∴x=±3,y=±5,
∵第二象限内的点P(x,y),
∴x<0,y>0,
∴x=﹣3,y=5,
∴点P的坐标为(﹣3,5),
故答案为:(﹣3,5).
三.解答题(共7小题)
19.【分析】(1)在平面直角坐标系中可以直接找出答案;
(2)根据求出的各点坐标,得出规律;
(3)点A100中的n正好是4的倍数,根据第二问的答案可以分别得出点A100和A101的坐标,所以可以得到蚂蚁从点A100到A101的移动方向.
【解答】解:(1)A1(0,1),A3(1,0),A12(6,0);
(2)当n=1时,A4(2,0),
当n=2时,A8(4,0),
当n=3时,A12(6,0),
所以A4n(2n,0);
(3)点A100中的n正好是4的倍数,所以点A100和A101的坐标分别是A100(50,0),A101的(50,1),所以蚂蚁从点A100到A101的移动方向是从下向上. 21世纪教育网版权所有
20.【分析】过点P作x轴的平行线PE交BC于点E,根据点B、C的坐标利用待定系数法求出直线BC的解析式,结合点P的坐标即可得出点E的坐标,根据三角形的面积公式结合△PAD与△PBC的面积相等,即可得出关于n﹣m的一元一次方程,解方程即可得出结论.【来源:21·世纪·教育·网】
【解答】解:过点P作x轴的平行线PE交BC于点E,如图所示.
设直线BC的解析式为y=kx+b,
将点B(a,m+1)、C(3,m+3)代入y=kx+b中,
得:,解得:,
∴直线BC的解析式为y=x+m+.
当y=n时,x=,
∴E(,n),PE=﹣(n﹣m)=.
∵A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),P(n﹣m,n),
∴AD=a﹣1,
∴S△PAD=AD?(xP﹣xA)=(a﹣1)?(n﹣m﹣1),S△PBC=PE?(yC﹣yB)=×2=.
∵S△PAD=S△PBC,
∴(a﹣1)?(n﹣m﹣1)=,
解得:n﹣m=2.
21.【分析】(1)利用点C和点C1的坐标变化得到平移的方向与距离,然后利用此平移规律写出顶点A1,B1的坐标;21·cn·jy·com
(2)根据关于原点对称的点的坐标特征求解;
(3)利用网格和旋转的性质画出△A2B3C3,然后写出△A2B3C3的各顶点的坐标.
【解答】解:(1)如图,△A1B1C1为所作,
因为点C(﹣1,3)平移后的对应点C1的坐标为(4,0),
所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,
所以点A1的坐标为(2,2),B1点的坐标为(3,﹣2);
(2)因为△ABC和△A1B2C2关于原点O成中心对称图形,
所以A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);
(3)如图,△A2B3C3为所作,A3(5,3),B3(1,2),C3(3,1);
22.【分析】(1)根据对称的性质,分别找出两对称点连线的中点即可;
(2)先求出点P的坐标,再根据a的大小分类讨论.当0<a≤6时,根据S△PAB=S梯形APP′O﹣S△AOB﹣S△BPP′求得a;当当6<a<7时,根据S△PAB=S梯形APP′O+S△BPP′﹣S△AOB求得a;当a>7时,S△PAB=S△AOB﹣S梯形APP′O﹣S△BPP′求得a.
【解答】解:(1)由图可知,点C与C′关于点(﹣1,3)对称; 点C与C″关于点(2,2)对称;点C与D关于点(﹣1,2)对称;
故答案为:(﹣1,3),(2,2),(﹣1,2);
(2)点C关于点(4,2)的对称点P(6,1),过P作x轴垂线交x轴于点P′,
(i)如图1,当0<a≤6时,则S△PAB=S梯形APP′O﹣S△AOB﹣S△BPP′,
5=×(1+a)×6﹣a2﹣×(6﹣a)×1,
解得a1=2,a2=5.
(ii)如图2,当6<a<7时,S△PAB=S梯形APP′O+S△BPP′﹣S△AOB,
5=+×(a﹣6)×1﹣a2,
解得a1=2(舍),a2=5(舍),
(iii)如图3,当a>7时,S△PAB=S△AOB﹣S梯形APP′O﹣S△BPP′,
5=a2﹣×(1+a)×6﹣×(a﹣6)×1,
解得a=或(舍).
综合(i)(ii)(iii)可得,a的值为2或5或.
23.【分析】(1)利用x轴上点的坐标性质纵坐标为0,进而得出a的值,即可得出答案;
(2)利用y轴上点的坐标性质横坐标为0,进而得出a的值,即可得出答案;
(3)利用平行于y轴直线的性质,横坐标相等,进而得出a的值,进而得出答案;
(4)利用点P到x轴、y轴的距离相等,得出横纵坐标相等或相反数进而得出答案.
【解答】解:(1)∵点P(a﹣2,2a+8),在x轴上,
∴2a+8=0,
解得:a=﹣4,
故a﹣2=﹣4﹣2=﹣6,
则P(﹣6,0);
(2))∵点P(a﹣2,2a+8),在y轴上,
∴a﹣2=0,
解得:a=2,
故2a+8=2×2+8=12,
则P(0,12);
(3)∵点Q的坐标为(1,5),直线PQ∥y轴;,
∴a﹣2=1,
解得:a=3,
故2a+8=14,
则P(1,14);
(4)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
故当a=﹣10则:a﹣2=﹣12,2a+8=﹣12,
则P(﹣12,﹣12);
故当a=﹣2则:a﹣2=﹣4,2a+8=4,
则P(﹣4,4).
综上所述:P(﹣12,﹣12),(﹣4,4).
24.【分析】(1)根据轴对称的定义直接画出.
(2)由点位置直接写出坐标.
【解答】解:(1)如图所示:
(2)点C1的坐标为:(4,3).
25.【分析】(1)CD的长为A、B两点的横坐标之差的绝对值;|DB﹣AC|为A、B两点的纵坐标之差的绝对值;www.21-cn-jy.com
(2)写出两点间的距离公式;
(3)利用两点间的距离公式计算.
【解答】解:(1)CD=|c﹣a|,|DB﹣AC|=|b﹣d|;
(2)AB=;
(3)AB==3.
故答案为|c﹣a|,|b﹣d|;.
第三章《位置与坐标》A
一.选择题(共12小题)
1.(2015?北京)如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,﹣1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( ) 21*cnjy*com
A.景仁宫(4,2)? B.养心殿(﹣2,3)
C.保和殿(1,0) D.武英殿(﹣3.5,﹣4)
2.(2016?大连)在平面直角坐标系中,点(1,5)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.(2016?临夏州)已知点P(0,m)在y轴的负半轴上,则点M(﹣m,﹣m+1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(2016?柳州)如图,在平面直角坐标系中,点P的坐标为( )
A.(3,﹣2) B.(﹣2,3) C.(﹣3,2) D.(2,﹣3)
5.(2016?滨州)如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是( )
A.(2,﹣3) B.(2,3) C.(3,2) D.(3,﹣2)
6.(2016?成都)平面直角坐标系中,点P(﹣2,3)关于x轴对称的点的坐标为( )
A.(﹣2,﹣3) B.(2,﹣3) C.(﹣3,﹣2) D.(3,﹣2)
7.(2016?赤峰)平面直角坐标系内的点A(﹣1,2)与点B(﹣1,﹣2)关于( )
A.y轴对称 B.x轴对称 C.原点对称 D.直线y=x对称
8.(2016?武汉)已知点A(a,1)与点A′(5,b)关于坐标原点对称,则实数a、b的值是( )
A.a=5,b=1 B.a=﹣5,b=1 C.a=5,b=﹣1 D.a=﹣5,b=﹣1
9.(2015?贵港)在平面直角坐标系中,若点P(m,m﹣n)与点Q(﹣2,3)关于原点对称,则点M(m,n)在( )2-1-c-n-j-y
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.(2015?凉山州)在平面直角坐标系中,点P(﹣3,2)关于直线y=x对称点的坐标是( )
A.(﹣3,﹣2) B.(3,2) C.(2,﹣3) D.(3,﹣2)
11.(2016?安顺)如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )【出处:21教育名师】
A.(﹣2,﹣4) B.(﹣2,4) C.(2,﹣3) D.(﹣1,﹣3)
12.(2016?台湾)如图为A、B、C三点在坐标平面上的位置图.若A、B、C的x坐标的数字总和为a,y坐标的数字总和为b,则a﹣b之值为何?( )21教育名师原创作品
A.5 B.3 C.﹣3 D.﹣5
二.填空题(共6小题)
13.(2015?六盘水)观察中国象棋的棋盘,其中红方“马”的位置可以用一个数对(3,5)来表示,红“马”走完“马3进四”后到达B点,则表示B点位置的数对是: .21*cnjy*com
14.(2015?南京)在平面直角坐标系中,点A的坐标是(2,﹣3),作点A关于x轴的对称点,得到点A′,再作点A′关于y轴的对称点,得到点A″,则点A″的坐标是( , ).
15.(2016?黔南州)在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:
①△(a,b)=(﹣a,b);
②○(a,b)=(﹣a,﹣b);
③Ω(a,b)=(a,﹣b),
按照以上变换例如:△(○(1,2))=(1,﹣2),则○(Ω(3,4))等于 .
16.(2016?宜宾)在平面直角坐标系内,以点P(1,1)为圆心、为半径作圆,则该圆与y轴的交点坐标是 .
17.(2011?盐城)如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(﹣1,4).将△ABC沿y轴翻折到第一象限,则点C的对应点C′的坐标是 .
18.(2015?广元)若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是 .
三.解答题(共7小题)
19.(2011?安徽)在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图所示.
(1)填写下列各点的坐标:
A1( , ),
A3( , ),
A12( , );
(2)写出点A4n的坐标(n是正整数);
(3)指出蚂蚁从点A100到A101的移动方向.
20.(2016?厦门)如图,在平面直角坐标系中xOy中,已知点A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),m>0,1<a<3,点P(n﹣m,n)是四边形ABCD内的一点,且△PAD与△PBC的面积相等,求n﹣m的值.
21.(2016?聊城)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
22.(2012?大庆)在直角坐标系中,C(2,3),C′(﹣4,3),C″(2,1),D(﹣4,1),A(0,a),B(a,O)(a>0).
(1)结合坐标系用坐标填空.
点C与C′关于点 对称; 点C与C″关于点 对称;点C与D关于点 对称;
(2)设点C关于点(4,2)的对称点是点P,若△PAB的面积等于5,求a值.
23.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点Q的坐标为(1,5),直线PQ∥y轴;
(4)点P到x轴、y轴的距离相等.
24.如图,在直角坐标系中,A(﹣1,5),B(﹣3,0),C(﹣4,3).
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1.
(2)写出点C1的坐标.
25.已知,如图,点A(a,b),B(c,d)在平面直角坐标系中的任意两点,且AC⊥x轴于点C,BD⊥x轴于点D.
(1)CD= ,|DB﹣AC|= ;(用含a,b,c,d的代数式表示)
(2)请猜想:A,B两点之间的距离 ;
(3)利用猜想,若A(﹣2,5),B(4,﹣4),求AB两点之间的距离.
答案与解析
一.选择题(共12小题)
1.【分析】根据平面直角坐标系,找出相应的位置,然后写出坐标即可.
【解答】解:根据表示太和门的点的坐标为(0,﹣1),表示九龙壁的点的坐标为(4,1),
可得:原点是中和殿,
所以可得景仁宫(2,4),养心殿(﹣2,3),保和殿(0,1),武英殿(﹣3.5,﹣3),
故选B
2.【分析】根据各象限内点的坐标特征解答即可.
【解答】解:点(1,5)所在的象限是第一象限.
故选A.
3.【分析】根据y轴的负半轴上点的横坐标等于零,纵坐标小于零,可得m的值,根据不等式的性质,可得到答案.
【解答】解:由点P(0,m)在y轴的负半轴上,得
m<0.
由不等式的性质,得
﹣m>0,﹣m+1>1,
则点M(﹣m,﹣m+1)在第一象限,
故选:A.
4.【分析】根据平面直角坐标系以及点的坐标的 定义写出即可.
【解答】解:点P的坐标为(3,﹣2).
故选A.
5.【分析】由题目中A点坐标特征推导得出平面直角坐标系y轴的位置,再通过C、D点坐标特征结合正五边形的轴对称性质就可以得出E点坐标了.21教育网
【解答】解:∵点A坐标为(0,a),
∴点A在该平面直角坐标系的y轴上,
∵点C、D的坐标为(b,m),(c,m),
∴点C、D关于y轴对称,
∵正五边形ABCDE是轴对称图形,
∴该平面直角坐标系经过点A的y轴是正五边形ABCDE的一条对称轴,
∴点B、E也关于y轴对称,
∵点B的坐标为(﹣3,2),
∴点E的坐标为(3,2).
故选:C.
6.【分析】直接利用关于x轴对称点的性质,横坐标不变,纵坐标互为相反数,进而得出答案.
【解答】解:点P(﹣2,3)关于x轴对称的点的坐标为(﹣2,﹣3).
故选:A.
7.【分析】根据关于x轴对称点的坐标特点:纵坐标互为相反数,横坐标不变可得答案.
【解答】解:平面直角坐标系内的点A(﹣1,2)与点B(﹣1,﹣2)关于x轴对称.
故选:B.
8.【分析】根据关于原点对称的点的横坐标与纵坐标都互为相反数解答.
【解答】解:∵点A(a,1)与点A′(5,b)关于坐标原点对称,
∴a=﹣5,b=﹣1.
故选D.
9.【分析】根据平面内两点关于原点对称的点,横坐标与纵坐标都互为相反数,则m=2且n=﹣3,从而得出点M(m,n)所在的象限.21cnjy.com
【解答】解:根据平面内两点关于原点对称的点,横坐标与纵坐标都互为相反数,
∴m=2且m﹣n=﹣3,
∴m=2,n=5
∴点M(m,n)在第一象限,
故选A.
10.【分析】根据直线y=x是第一、三象限的角平分线,和点P的坐标结合图形得到答案.
【解答】解:点P关于直线y=x对称点为点Q,
作AP∥x轴交y=x于A,
∵y=x是第一、三象限的角平分线,
∴点A的坐标为(2,2),
∵AP=AQ,
∴点Q的坐标为(2,﹣3)
故选:C.
11.【分析】直接利用平移中点的变化规律求解即可.
【解答】解:由题意可知此题规律是(x+2,y﹣3),照此规律计算可知顶点P(﹣4,﹣1)平移后的坐标是(﹣2,﹣4).2·1·c·n·j·y
故选A.
12.【分析】先求出A、B、C三点的横坐标的和为﹣1+0+5=4,纵坐标的和为﹣4﹣1+4=﹣1,再把它们相减即可求得a﹣b之值.www-2-1-cnjy-com
【解答】解:由图形可知:
a=﹣1+0+5=4,
b=﹣4﹣1+4=﹣1,
a﹣b=4+1=5.
故选:A.
二.填空题(共6小题)
13.【分析】根据图示,写出点B的位置的数对即可.
【解答】解:如图所示,
B点位置的数对是(4,7).
故答案为:(4,7).
14.【分析】分别利用x轴、y轴对称点的性质,得出A′,A″的坐标进而得出答案.
【解答】解:∵点A的坐标是(2,﹣3),作点A关于x轴的对称点,得到点A′,
∴A′的坐标为:(2,3),
∵点A′关于y轴的对称点,得到点A″,
∴点A″的坐标是:(﹣2,3).
故答案为:﹣2;3.
15.【分析】根据三种变换规律的特点解答即可.
【解答】解:○(Ω(3,4))=○(3,﹣4)=(﹣3,4).
故答案为:(﹣3,4).
16.【分析】在平面直角坐标系中,根据勾股定理先求出直角三角形的另外一个直角边,再根据点P的坐标即可得出答案.21·世纪*教育网
【解答】解:以(1,1)为圆心,为半径画圆,与y轴相交,构成直角三角形,
用勾股定理计算得另一直角边的长为2,
则与y轴交点坐标为(0,3)或(0,﹣1).
故答案为:(0,3),(0,﹣1).
17.【分析】由点A的坐标为(﹣1,4),即可求得点C的坐标,又由将△ABC沿y轴翻折到第一象限,即可得点C与C′关于y轴对称,则可求得点C′的坐标.【来源:21cnj*y.co*m】
【解答】解:如图:∵点A的坐标为(﹣1,4),
∴点C的坐标为(﹣3,1),
∵将△ABC沿y轴翻折到第一象限,
∴点C的对应点C′的坐标是(3,1).
故答案为:(3,1).
18.【分析】根据绝对值的意义和平方根得到x=±5,y=±2,再根据第二象限的点的坐标特点得到x<0,y>0,于是x=﹣5,y=2,然后可直接写出P点坐标.【版权所有:21教育】
【解答】解:∵|x|=3,y2=25,
∴x=±3,y=±5,
∵第二象限内的点P(x,y),
∴x<0,y>0,
∴x=﹣3,y=5,
∴点P的坐标为(﹣3,5),
故答案为:(﹣3,5).
三.解答题(共7小题)
19.【分析】(1)在平面直角坐标系中可以直接找出答案;
(2)根据求出的各点坐标,得出规律;
(3)点A100中的n正好是4的倍数,根据第二问的答案可以分别得出点A100和A101的坐标,所以可以得到蚂蚁从点A100到A101的移动方向.
【解答】解:(1)A1(0,1),A3(1,0),A12(6,0);
(2)当n=1时,A4(2,0),
当n=2时,A8(4,0),
当n=3时,A12(6,0),
所以A4n(2n,0);
(3)点A100中的n正好是4的倍数,所以点A100和A101的坐标分别是A100(50,0),A101的(50,1),所以蚂蚁从点A100到A101的移动方向是从下向上. 21世纪教育网版权所有
20.【分析】过点P作x轴的平行线PE交BC于点E,根据点B、C的坐标利用待定系数法求出直线BC的解析式,结合点P的坐标即可得出点E的坐标,根据三角形的面积公式结合△PAD与△PBC的面积相等,即可得出关于n﹣m的一元一次方程,解方程即可得出结论.【来源:21·世纪·教育·网】
【解答】解:过点P作x轴的平行线PE交BC于点E,如图所示.
设直线BC的解析式为y=kx+b,
将点B(a,m+1)、C(3,m+3)代入y=kx+b中,
得:,解得:,
∴直线BC的解析式为y=x+m+.
当y=n时,x=,
∴E(,n),PE=﹣(n﹣m)=.
∵A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),P(n﹣m,n),
∴AD=a﹣1,
∴S△PAD=AD?(xP﹣xA)=(a﹣1)?(n﹣m﹣1),S△PBC=PE?(yC﹣yB)=×2=.
∵S△PAD=S△PBC,
∴(a﹣1)?(n﹣m﹣1)=,
解得:n﹣m=2.
21.【分析】(1)利用点C和点C1的坐标变化得到平移的方向与距离,然后利用此平移规律写出顶点A1,B1的坐标;21·cn·jy·com
(2)根据关于原点对称的点的坐标特征求解;
(3)利用网格和旋转的性质画出△A2B3C3,然后写出△A2B3C3的各顶点的坐标.
【解答】解:(1)如图,△A1B1C1为所作,
因为点C(﹣1,3)平移后的对应点C1的坐标为(4,0),
所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,
所以点A1的坐标为(2,2),B1点的坐标为(3,﹣2);
(2)因为△ABC和△A1B2C2关于原点O成中心对称图形,
所以A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);
(3)如图,△A2B3C3为所作,A3(5,3),B3(1,2),C3(3,1);
22.【分析】(1)根据对称的性质,分别找出两对称点连线的中点即可;
(2)先求出点P的坐标,再根据a的大小分类讨论.当0<a≤6时,根据S△PAB=S梯形APP′O﹣S△AOB﹣S△BPP′求得a;当当6<a<7时,根据S△PAB=S梯形APP′O+S△BPP′﹣S△AOB求得a;当a>7时,S△PAB=S△AOB﹣S梯形APP′O﹣S△BPP′求得a.
【解答】解:(1)由图可知,点C与C′关于点(﹣1,3)对称; 点C与C″关于点(2,2)对称;点C与D关于点(﹣1,2)对称;
故答案为:(﹣1,3),(2,2),(﹣1,2);
(2)点C关于点(4,2)的对称点P(6,1),过P作x轴垂线交x轴于点P′,
(i)如图1,当0<a≤6时,则S△PAB=S梯形APP′O﹣S△AOB﹣S△BPP′,
5=×(1+a)×6﹣a2﹣×(6﹣a)×1,
解得a1=2,a2=5.
(ii)如图2,当6<a<7时,S△PAB=S梯形APP′O+S△BPP′﹣S△AOB,
5=+×(a﹣6)×1﹣a2,
解得a1=2(舍),a2=5(舍),
(iii)如图3,当a>7时,S△PAB=S△AOB﹣S梯形APP′O﹣S△BPP′,
5=a2﹣×(1+a)×6﹣×(a﹣6)×1,
解得a=或(舍).
综合(i)(ii)(iii)可得,a的值为2或5或.
23.【分析】(1)利用x轴上点的坐标性质纵坐标为0,进而得出a的值,即可得出答案;
(2)利用y轴上点的坐标性质横坐标为0,进而得出a的值,即可得出答案;
(3)利用平行于y轴直线的性质,横坐标相等,进而得出a的值,进而得出答案;
(4)利用点P到x轴、y轴的距离相等,得出横纵坐标相等或相反数进而得出答案.
【解答】解:(1)∵点P(a﹣2,2a+8),在x轴上,
∴2a+8=0,
解得:a=﹣4,
故a﹣2=﹣4﹣2=﹣6,
则P(﹣6,0);
(2))∵点P(a﹣2,2a+8),在y轴上,
∴a﹣2=0,
解得:a=2,
故2a+8=2×2+8=12,
则P(0,12);
(3)∵点Q的坐标为(1,5),直线PQ∥y轴;,
∴a﹣2=1,
解得:a=3,
故2a+8=14,
则P(1,14);
(4)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
故当a=﹣10则:a﹣2=﹣12,2a+8=﹣12,
则P(﹣12,﹣12);
故当a=﹣2则:a﹣2=﹣4,2a+8=4,
则P(﹣4,4).
综上所述:P(﹣12,﹣12),(﹣4,4).
24.【分析】(1)根据轴对称的定义直接画出.
(2)由点位置直接写出坐标.
【解答】解:(1)如图所示:
(2)点C1的坐标为:(4,3).
25.【分析】(1)CD的长为A、B两点的横坐标之差的绝对值;|DB﹣AC|为A、B两点的纵坐标之差的绝对值;www.21-cn-jy.com
(2)写出两点间的距离公式;
(3)利用两点间的距离公式计算.
【解答】解:(1)CD=|c﹣a|,|DB﹣AC|=|b﹣d|;
(2)AB=;
(3)AB==3.
故答案为|c﹣a|,|b﹣d|;.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
