三角形的外角
图片预览





文档简介
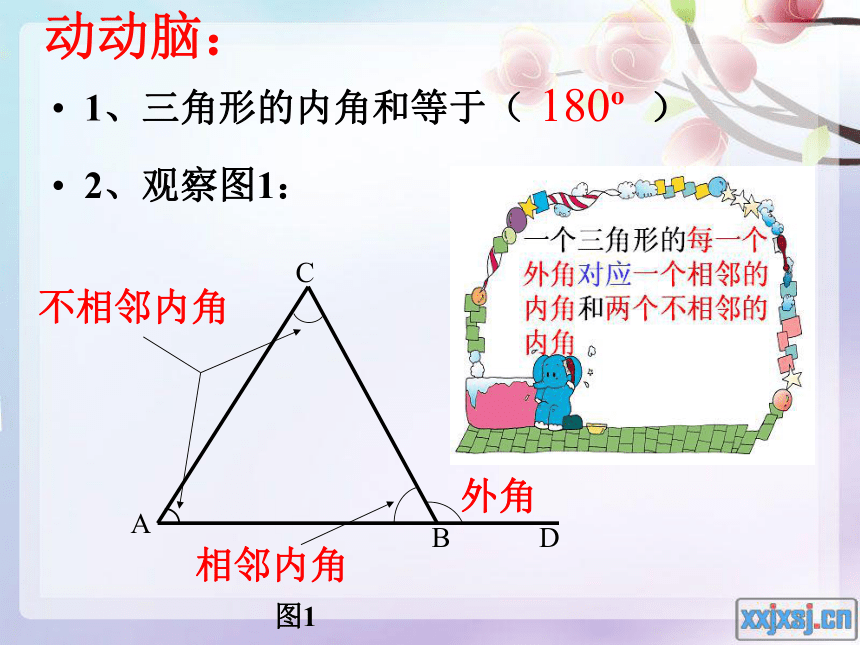
课件40张PPT。7.2.2 三角形的外角动动脑:1、三角形的内角和等于( )外角180o2、观察图1:为承办北京2008奥林匹克运动会,对某体育场馆进出礼堂的地面图案进行了招标。以下是某公司设计的地面图案的一部分: ABCDE 40o60o
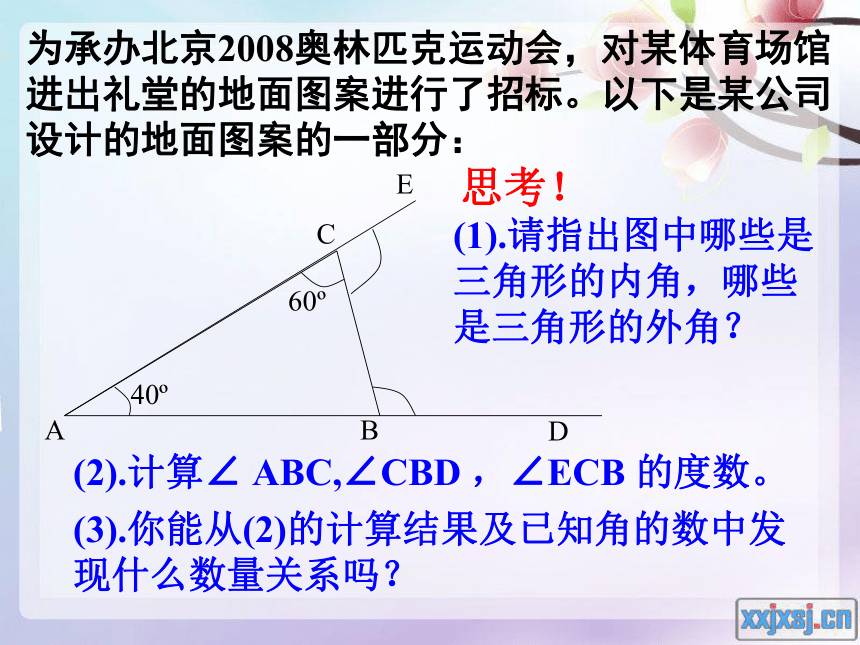
思考!(1).请指出图中哪些是三角形的内角,哪些是三角形的外角?(2).计算∠ ABC,∠CBD ,∠ECB 的度数。(3).你能从(2)的计算结果及已知角的数中发现什么数量关系吗?解:因为∠CAD+∠BAC=180o三角形外角的性质:
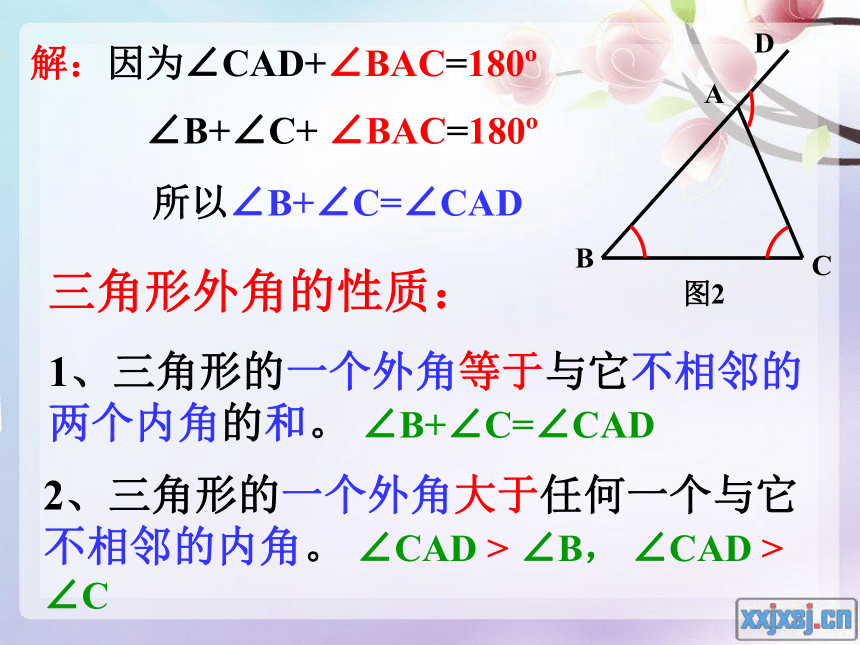
1、三角形的一个外角等于与它不相邻的两个内角的和。 ∠B+∠C=∠CAD∠B+∠C+ ∠BAC=180o 所以∠B+∠C=∠CAD2、三角形的一个外角大于任何一个与它不相邻的内角。 ∠CAD > ∠B, ∠CAD > ∠C2.三角形的一个外角大于任何一个
与它不相邻的内角。三角形的外角的两条性质:1.三角形的一个外角等于
与它不相邻的两个内角的和; 三角形的外角的性质: 性质1:三角形的一个外角等于与它不相邻的两个内角的和;性质2:三角形的一个外角大于任何一个与它不相邻的内角。 ∠4 =
∠5 =
∠6 =∠2 + ∠35261∠1 + ∠3∠1 + ∠2∠4 >
∠5 >
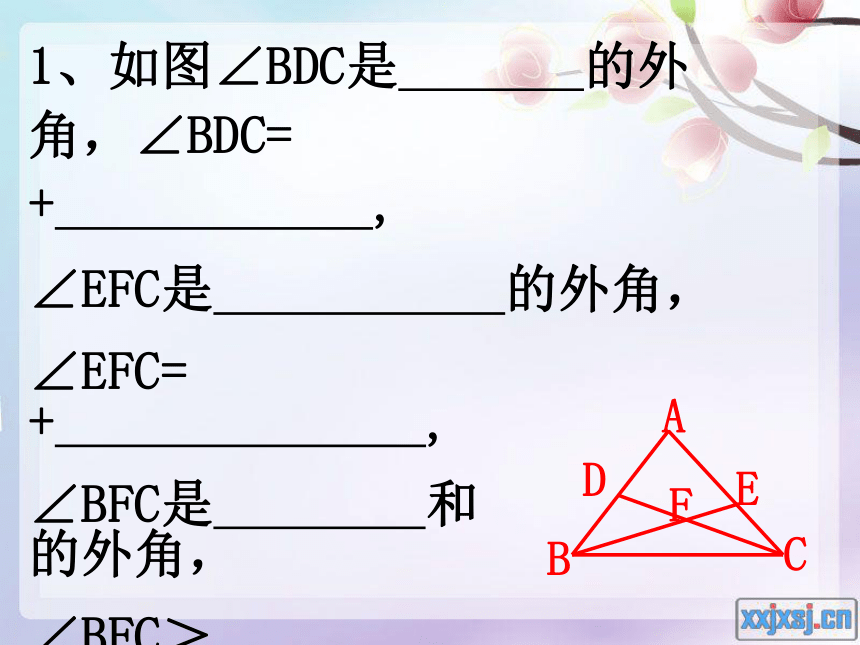
∠6 >∠2 (或 ∠3 )∠1 (或 ∠3 )∠1 (或 ∠2 )431、如图∠BDC是 的外角,∠BDC= + ,
∠EFC是 的外角,
∠EFC= + ,
∠BFC是 和 的外角,
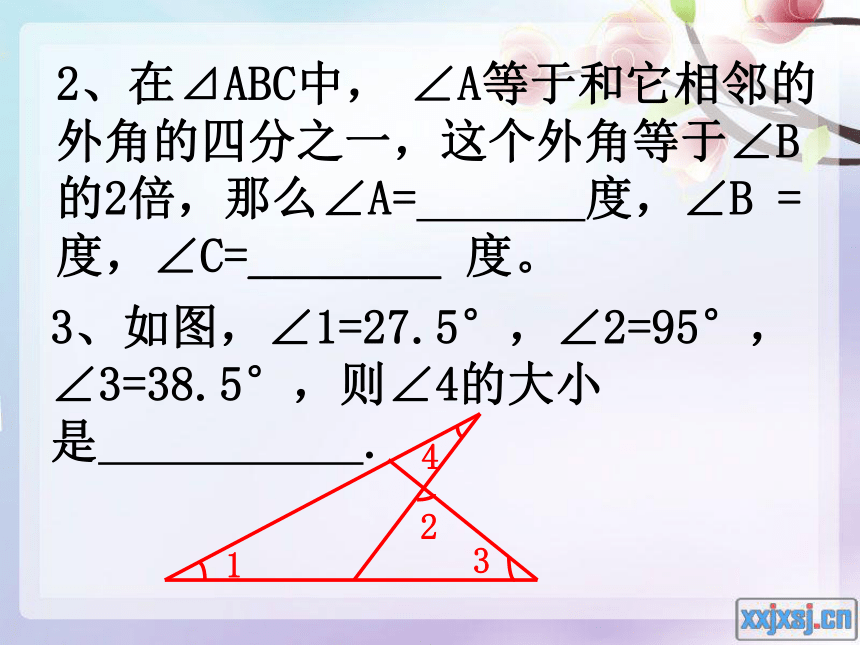
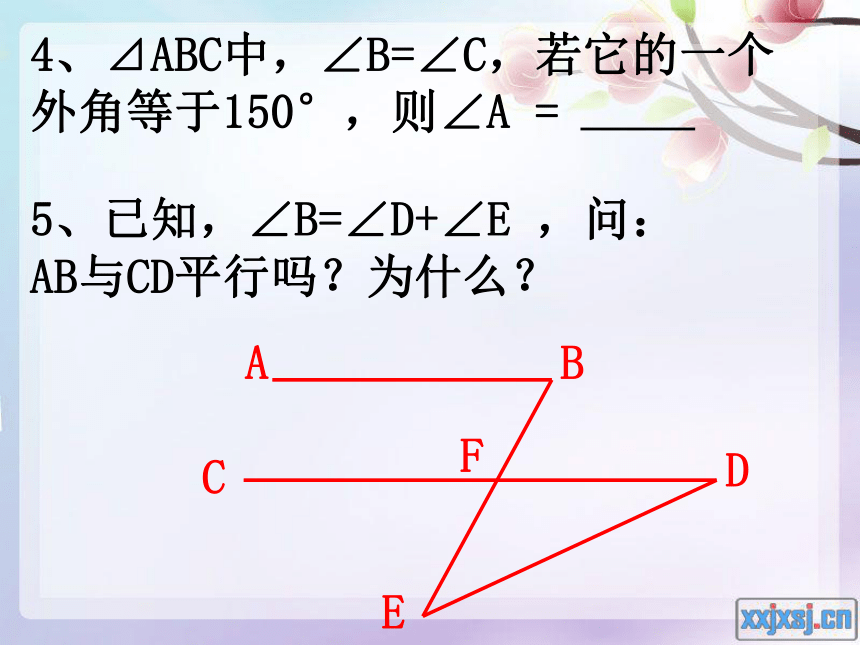
∠BFC> > .2、在⊿ABC中, ∠A等于和它相邻的外角的四分之一,这个外角等于∠B的2倍,那么∠A= 度,∠B = 度,∠C=________ 度。3、如图,∠1=27.5°,∠2=95°, ∠3=38.5°,则∠4的大小是 .6、如图, ⊿ABC的一个角被纸挡住了,请你根据以下问题中的条件填空:
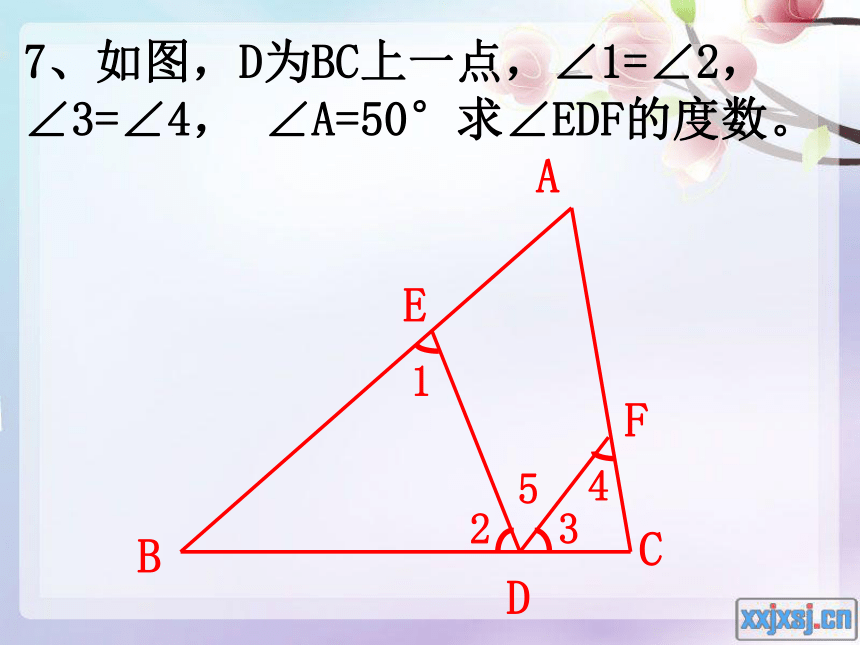
7、如图,D为BC上一点,∠1=∠2,
∠3=∠4, ∠A=50°求∠EDF的度数。58、如图,∠BOC=138°,∠B=36°,∠C=30°,
求∠A的度数。9、如图,P是⊿ABC内任意一点
求证:∠BPC>∠A 10、如图,⊿ABC中,AD⊥BC
于D,AE平分∠BAC ,∠B=80°
∠C=46°求∠DAE的度数。ABCDE问1:小明从点C出发,按逆时针方向绕△ABC跑
一圈, 身体转过的角度之和是多少?答1:∠1+∠2+∠3=360°问2:对于△ABC来说,∠1、∠2、∠3的共同
特征是什么?答2:∠1、∠2、∠3都是三角形的一
边与另一边的延长线组成的角,
叫做三角形的外角。 问3:一个三角形共有几个外角呢?答3:一个三角形共有6个外角。三角形外角的性质:性质 1:三角形的三个外角的和是360°。思考:如图,∠ ACD与∠ A、 ∠ B有什么关系?性质 2:三角形的一个外角等于与它不相邻的两
个内角的和。推论1:三角形的一个外角大于与它不相邻的任何一
个内角。1、看图填空,根据图中所示角的度数,求出其中
∠α的度数。2、三角形的一个外角与它相邻的内角相等,而且等于
与它不相邻的两角中一角的3倍,则这个三角形各角的
度数是______________。3、三角形的三个外角中,最多可以有____个锐角
______个直角______个钝角。4、三角形的三个外角中,钝角的个数至少是 ( )
A、0个 B 、1个
C 、2个 D 、3个5、如图,在△ABC中, ∠ A=90°, ∠ D是∠ B,
∠ C外角平分线的夹角,求∠ D的度数。6、如图:已知∠A=20°, ∠ B=162 ° ,
∠ C=27 ° ,则∠ D=______。7.求五角星的五个角的度数之和.8.如图,A 、 B 、 C 、 D 、 E 、 F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E +∠F 的度数为 ( )
(A) 180 ° (B) 360 ° (C) 540 ° (D) 720 °
B9、如图∠1是△ABC的一个外角,E为边AC上一点,
延长BC到D,连结DE,试说明∠1 >∠2的理由。10、如图,在△ABC中,D是BC边上一点, ∠1 =∠2,
∠3 =∠4, ∠BAC=60°,求∠ DAC的度数。11、如图所示下列说法一定正确的是 ( )
A、 ∠ B> ∠ ACD
B 、 ∠ B+ ∠ ACB=180°-∠ A
C 、 ∠ B+ ∠ ACB<180 °
D 、 ∠ HEC > ∠ BABCDEF练习:
1.求下列图中∠1的度数。
30o60o120o30o45o50o11112390oBCO2.判断∠1与∠2的大小,并说明理由。3.如图,计算∠BOC20o30oA90o85o95o60o43o30o例1:求下列各图中∠α的度数。性质1:三角形的一个外角等于与它不相邻的两个内角的和解:
因为∠ 1是△DEC的外角所以∠ 1 >∠ CDE同理∠ CDE >∠B所以∠ 1 >∠ B性质2:三角形的一个外角大于任何一个与它不相邻的内角性质2:三角形的一个外角大于任何一个与它不相邻的内角性质1:三角形的一个外角等于与它不相邻的两个内角的和练习1:(口答)一个三角形可以有两个内角都是直角吗?可以有两个内角都是钝角或都是锐角吗?为什么?练习2:你能根据三角形外角的特征把三角形分类吗?请与同学交流你的想法 。锐角三角形直角三角形钝角三角形练习3:如图4,五角星ABCDE中,请你求出∠A +∠B+∠C+∠D+∠E的度数。解:∵∠AFE是△FCE的外角∴∠AFE=∠C+ ∠E同理∠AGB=∠B+∠D在△AFG中
∠A+∠AFE+∠AGB=180o∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180o性质2:三角形的一个外角大于任何一个与它不相邻的内角性质1:三角形的一个外角等于与它不相邻的两个内角的和ABCD 你能由下图说明三角形的外角和
等于360o,这一结论吗?例:如图,D是△ ABC的BC边上一点,
∠ B= ∠ BAD, ∠ ADC=80o,∠ BAC=70o,
求:(1) ∠ B的度数;
(2) ∠ C的度数。ABCD 例2:如图,类似于三角形,我们称
∠1+ ∠2+ ∠3+ ∠4为四边行的外角和,
已知四边形的内角和为360o,你能用今
天所学的方法进行推理计算吗? 1234ABCD三角形的外角和的规定从与每一个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和。
如图:你有几种方法计算∠1+∠2+∠3=?ABC123试试看,你能不能独立完成下面一题.例1如图8.2.9,D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°,
∠ BAC=70°.求:
(1)∠B的度数;
(2)∠C的度数解 (1)因为∠ADC是△ABD的外角,所以
∠ADC=∠B+∠BAD=80°.
又 ∠B=∠BAD,
所以∠B=80°÷ 2=40°.
(2)在△ABC中,因为
∠B+∠BAC+∠C=180°,
所以∠C=180°-∠B-∠BAC
=180°-40°-70°
=70° 例2:如图,已知BCD、CAE、AFB是直线 , 试比较∠1与∠2的大小。CDFAEB12解:∵BCD是直线(已知),
∴ ∠2是△ABC外角(外角的定义),
BCDAFE12∴∠2 〉∠BAC (三角形的一个外
角大于和它不 相邻的任一内角)。
∵EAC、AFB是直线(已知)∴∠BAC 〉∠1 (为什么?)
∴∠2 〉∠1,即∠2 比∠1大。
∴∠BAC是△AEF的外角检验一下自己的知识够用不?(巩固练习):1) 求下列各图中∠1的度数。(2)如果∠C=4∠A,∠A+∠B=100°,
那么∠A= ∠B=
与∠C相邻的外角= 20 °80 °100°3)如图,在直角△ABC中,CD是斜边AB上的高,
∠BCD=35°,求∠A与∠EBC的度数.
思考!(1).请指出图中哪些是三角形的内角,哪些是三角形的外角?(2).计算∠ ABC,∠CBD ,∠ECB 的度数。(3).你能从(2)的计算结果及已知角的数中发现什么数量关系吗?解:因为∠CAD+∠BAC=180o三角形外角的性质:
1、三角形的一个外角等于与它不相邻的两个内角的和。 ∠B+∠C=∠CAD∠B+∠C+ ∠BAC=180o 所以∠B+∠C=∠CAD2、三角形的一个外角大于任何一个与它不相邻的内角。 ∠CAD > ∠B, ∠CAD > ∠C2.三角形的一个外角大于任何一个
与它不相邻的内角。三角形的外角的两条性质:1.三角形的一个外角等于
与它不相邻的两个内角的和; 三角形的外角的性质: 性质1:三角形的一个外角等于与它不相邻的两个内角的和;性质2:三角形的一个外角大于任何一个与它不相邻的内角。 ∠4 =
∠5 =
∠6 =∠2 + ∠35261∠1 + ∠3∠1 + ∠2∠4 >
∠5 >
∠6 >∠2 (或 ∠3 )∠1 (或 ∠3 )∠1 (或 ∠2 )431、如图∠BDC是 的外角,∠BDC= + ,
∠EFC是 的外角,
∠EFC= + ,
∠BFC是 和 的外角,
∠BFC> > .2、在⊿ABC中, ∠A等于和它相邻的外角的四分之一,这个外角等于∠B的2倍,那么∠A= 度,∠B = 度,∠C=________ 度。3、如图,∠1=27.5°,∠2=95°, ∠3=38.5°,则∠4的大小是 .6、如图, ⊿ABC的一个角被纸挡住了,请你根据以下问题中的条件填空:
7、如图,D为BC上一点,∠1=∠2,
∠3=∠4, ∠A=50°求∠EDF的度数。58、如图,∠BOC=138°,∠B=36°,∠C=30°,
求∠A的度数。9、如图,P是⊿ABC内任意一点
求证:∠BPC>∠A 10、如图,⊿ABC中,AD⊥BC
于D,AE平分∠BAC ,∠B=80°
∠C=46°求∠DAE的度数。ABCDE问1:小明从点C出发,按逆时针方向绕△ABC跑
一圈, 身体转过的角度之和是多少?答1:∠1+∠2+∠3=360°问2:对于△ABC来说,∠1、∠2、∠3的共同
特征是什么?答2:∠1、∠2、∠3都是三角形的一
边与另一边的延长线组成的角,
叫做三角形的外角。 问3:一个三角形共有几个外角呢?答3:一个三角形共有6个外角。三角形外角的性质:性质 1:三角形的三个外角的和是360°。思考:如图,∠ ACD与∠ A、 ∠ B有什么关系?性质 2:三角形的一个外角等于与它不相邻的两
个内角的和。推论1:三角形的一个外角大于与它不相邻的任何一
个内角。1、看图填空,根据图中所示角的度数,求出其中
∠α的度数。2、三角形的一个外角与它相邻的内角相等,而且等于
与它不相邻的两角中一角的3倍,则这个三角形各角的
度数是______________。3、三角形的三个外角中,最多可以有____个锐角
______个直角______个钝角。4、三角形的三个外角中,钝角的个数至少是 ( )
A、0个 B 、1个
C 、2个 D 、3个5、如图,在△ABC中, ∠ A=90°, ∠ D是∠ B,
∠ C外角平分线的夹角,求∠ D的度数。6、如图:已知∠A=20°, ∠ B=162 ° ,
∠ C=27 ° ,则∠ D=______。7.求五角星的五个角的度数之和.8.如图,A 、 B 、 C 、 D 、 E 、 F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E +∠F 的度数为 ( )
(A) 180 ° (B) 360 ° (C) 540 ° (D) 720 °
B9、如图∠1是△ABC的一个外角,E为边AC上一点,
延长BC到D,连结DE,试说明∠1 >∠2的理由。10、如图,在△ABC中,D是BC边上一点, ∠1 =∠2,
∠3 =∠4, ∠BAC=60°,求∠ DAC的度数。11、如图所示下列说法一定正确的是 ( )
A、 ∠ B> ∠ ACD
B 、 ∠ B+ ∠ ACB=180°-∠ A
C 、 ∠ B+ ∠ ACB<180 °
D 、 ∠ HEC > ∠ BABCDEF练习:
1.求下列图中∠1的度数。
30o60o120o30o45o50o11112390oBCO2.判断∠1与∠2的大小,并说明理由。3.如图,计算∠BOC20o30oA90o85o95o60o43o30o例1:求下列各图中∠α的度数。性质1:三角形的一个外角等于与它不相邻的两个内角的和解:
因为∠ 1是△DEC的外角所以∠ 1 >∠ CDE同理∠ CDE >∠B所以∠ 1 >∠ B性质2:三角形的一个外角大于任何一个与它不相邻的内角性质2:三角形的一个外角大于任何一个与它不相邻的内角性质1:三角形的一个外角等于与它不相邻的两个内角的和练习1:(口答)一个三角形可以有两个内角都是直角吗?可以有两个内角都是钝角或都是锐角吗?为什么?练习2:你能根据三角形外角的特征把三角形分类吗?请与同学交流你的想法 。锐角三角形直角三角形钝角三角形练习3:如图4,五角星ABCDE中,请你求出∠A +∠B+∠C+∠D+∠E的度数。解:∵∠AFE是△FCE的外角∴∠AFE=∠C+ ∠E同理∠AGB=∠B+∠D在△AFG中
∠A+∠AFE+∠AGB=180o∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180o性质2:三角形的一个外角大于任何一个与它不相邻的内角性质1:三角形的一个外角等于与它不相邻的两个内角的和ABCD 你能由下图说明三角形的外角和
等于360o,这一结论吗?例:如图,D是△ ABC的BC边上一点,
∠ B= ∠ BAD, ∠ ADC=80o,∠ BAC=70o,
求:(1) ∠ B的度数;
(2) ∠ C的度数。ABCD 例2:如图,类似于三角形,我们称
∠1+ ∠2+ ∠3+ ∠4为四边行的外角和,
已知四边形的内角和为360o,你能用今
天所学的方法进行推理计算吗? 1234ABCD三角形的外角和的规定从与每一个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和。
如图:你有几种方法计算∠1+∠2+∠3=?ABC123试试看,你能不能独立完成下面一题.例1如图8.2.9,D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°,
∠ BAC=70°.求:
(1)∠B的度数;
(2)∠C的度数解 (1)因为∠ADC是△ABD的外角,所以
∠ADC=∠B+∠BAD=80°.
又 ∠B=∠BAD,
所以∠B=80°÷ 2=40°.
(2)在△ABC中,因为
∠B+∠BAC+∠C=180°,
所以∠C=180°-∠B-∠BAC
=180°-40°-70°
=70° 例2:如图,已知BCD、CAE、AFB是直线 , 试比较∠1与∠2的大小。CDFAEB12解:∵BCD是直线(已知),
∴ ∠2是△ABC外角(外角的定义),
BCDAFE12∴∠2 〉∠BAC (三角形的一个外
角大于和它不 相邻的任一内角)。
∵EAC、AFB是直线(已知)∴∠BAC 〉∠1 (为什么?)
∴∠2 〉∠1,即∠2 比∠1大。
∴∠BAC是△AEF的外角检验一下自己的知识够用不?(巩固练习):1) 求下列各图中∠1的度数。(2)如果∠C=4∠A,∠A+∠B=100°,
那么∠A= ∠B=
与∠C相邻的外角= 20 °80 °100°3)如图,在直角△ABC中,CD是斜边AB上的高,
∠BCD=35°,求∠A与∠EBC的度数.
