苏科版八年级上第二章轴对称图形阶段测试(2.4-2.5)(答案不全)
文档属性
| 名称 | 苏科版八年级上第二章轴对称图形阶段测试(2.4-2.5)(答案不全) |  | |
| 格式 | zip | ||
| 文件大小 | 132.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-14 11:02:59 | ||
图片预览

文档简介
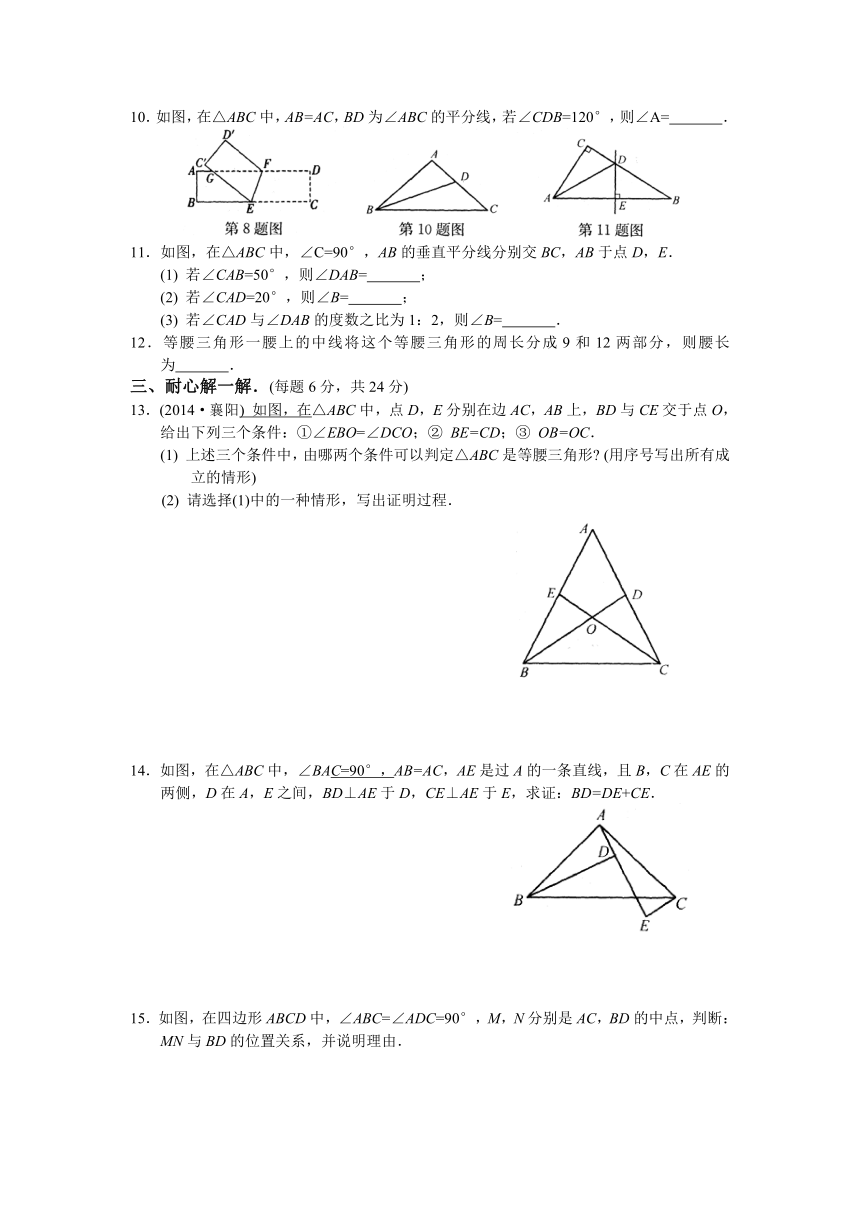
第二章
轴对称图形
阶段测试(2.4~2.5)
一、细心选一选.(每小题4分,共28分)
1.若一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为
(
)
A.20°
B.120°
C.20°或120°
D.
36°
2.(2014·威海改编)
如图,在△A
( http: / / www.21cnjy.com )BC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,下列结论错误的是
(
)
A.∠C=2∠A
B.BD平分∠ABC
C.S△BCD=S△BOD
D.图中有3个等腰三角形
( http: / / www.21cnjy.com )
3.如图,在△ABC中,点D,E,F分别在
( http: / / www.21cnjy.com )边BC,AB,AC上,且BD=BE,CD=CF,∠A=70°,那么∠FDE等于
(
)
A.40°
B.45°
C.55°
D.60°
4.(2014·茂名)
如图,地面上有三个
( http: / / www.21cnjy.com )洞口A,B,C,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及三个洞口
(到A,B,C三个点的距离相等),尽快抓到老鼠,应该蹲守在
(
)
A.△ABC三边垂直平分线的交点
B.△ABC三条角平分线的交点
C.△ABC三条高所在直线的交点
D.△ABC三条中线的交点
5.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=5,BC=8,则△EFM的周长是
(
)
A.21
B.18
C.13
D
15
( http: / / www.21cnjy.com )
6.如图,在△ABC中,A
( http: / / www.21cnjy.com )B=AC,∠A=36°,BD,CE分别是△ABC,△BCD的角平分线,则图中的等腰三角形有
(
)
A.5个
B.4个
C.3个
D.2个
7.如图,∠MON=30°,点A1,A
( http: / / www.21cnjy.com )2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=1,则△A6
B6
A7的边长为
(
)
二、认真填一填.(每空4分,共28分)
8.(2014·宿迁)
如图,将一
( http: / / www.21cnjy.com )张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C',D'处,C'E交AF于点G,若∠CEF=70°,则∠GFD'=
°.
9.已知等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为40°,此等腰三角形的顶角的度数为
.
10.如图,在△ABC中,AB=AC,BD为∠ABC的平分线,若∠CDB=120°,则∠A=
.
( http: / / www.21cnjy.com )
11.如图,在△ABC中,∠C=90°,AB的垂直平分线分别交BC,AB于点D,E.
(1)
若∠CAB=50°,则∠DAB=
;
(2)
若∠CAD=20°,则∠B=
;
(3)
若∠CAD与∠DAB的度数之比为1:2,则∠B=
.
12.等腰三角形一腰上的中线将这个等腰三角形的周长分成9和12两部分,则腰长为
.
三、耐心解一解.(每题6分,共24分)
13.(2014·襄阳)
如图,在
( http: / / www.21cnjy.com )△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②
BE=CD;③
OB=OC.
(1)
上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形
(用序号写出所有成立的情形)
(2)
请选择(1)中的一种情形,写出证明过程.
( http: / / www.21cnjy.com )
14.如图,在△ABC中,∠BAC=90°,
( http: / / www.21cnjy.com )AB=AC,AE是过A的一条直线,且B,C在AE的两侧,D在A,E之间,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
( http: / / www.21cnjy.com )
15.如图,在四边形ABCD中,∠ABC=∠ADC=90°,M,N分别是AC,BD的中点,判断:MN与BD的位置关系,并说明理由.
( http: / / www.21cnjy.com )
16.如图,P是等边△ABC内的一点,连接PA,PB,PC,以BP为边作等边△BPM,连接CM.
(1)
观察并猜想AP与CM之间的大小关系,并说明你的理由;
(2)
若∠APC=100°,
△PMC为直角三角形,求.∠BPC的度数.
( http: / / www.21cnjy.com )
拓展提优
17.(本题8分)
(1)
如图(1)
( http: / / www.21cnjy.com ),O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小;
(2)
如图(2),△O
( http: / / www.21cnjy.com )AB固定不动,保持△OCD的形状和大小不变,将△OCD绕着点O旋转(△OAB和△OCD不能重叠).求∠AEB的大小.
( http: / / www.21cnjy.com )
18.(本题12分)
(2014·东营)
(1)
如图①,已知:在△AB
( http: / / www.21cnjy.com )C中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E证明:DE=BD+CE.
(2)
如图②,将(1)中的条
( http: / / www.21cnjy.com )件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立
如成立,请你给出证明;若不成立,请说明理由.
(3)
拓展与应用:如图③
( http: / / www.21cnjy.com ),D,E是D,A,E三点所在直线m上的两动点(D,A,E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
( http: / / www.21cnjy.com )
阶段测试(二)
1.C
2.C
3.C
4.A
5.C
6.A
7.C
8.40°
9.50或130°
10.100°
11.40°
35°
( http: / / www.21cnjy.com )36°
12.6或8
13.略
14.∵∠CAE+∠BAD=90°,∠BAD+∠ABD=90°,∴∠CAE=∠ABD.∵∠ADB=∠AEC=90°,AB=AC,∴△ABD≌△CAE.∴AD=CE,BD=AE.∵AE=AD+DE=CE+DE,∴BD=DE+CE
15.MN垂直平分BD
提示:连接BM,DM,证BM=AC,DM=AC,则BM=DM,再用三线合一证MN垂直平分BD.
16.(1)
AP=CM,证△ABP≌△CBM
(2)
110°或150°
17.略
18.证明:(1)
∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=90°.∵∠BAC=90°,∴∠BAD+∠CAE=90°.∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD.
又AB=AC,∴△ADB≌△CEA.∴AE=BD,AD=CE.∴DE=AE+AD=BD+CE.
(2)
∵∠B=∠BAC
=α,∴∠DBA+∠BAD=
∠BAD+∠CAE=180°-α.
( http: / / www.21cnjy.com )∴∠DBA=∠CAE.∵∠BDA=∠AEC=α,AB=AC.∴△ADB≌△CEA.∴AE=BD,AD=CE.∴DE=AE+AD=BD+CE
(3)由(2)知,△ADB≌△CEA,BD=AE,∠DBA=∠CAE.∵△ABF和△ACF均为等边三角形,∴∠ABF=∠CAF=60°.∴∠DBA+
∠ABF=∠CAE+∠CAF.∴∠DB
( http: / / www.21cnjy.com )F=∠FAE.∵BF=AF,∴△DBF≌△EAF.∴DF=EF,∠BFD=∠AFE.∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°.∴△DEF为等边三角形.
轴对称图形
阶段测试(2.4~2.5)
一、细心选一选.(每小题4分,共28分)
1.若一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为
(
)
A.20°
B.120°
C.20°或120°
D.
36°
2.(2014·威海改编)
如图,在△A
( http: / / www.21cnjy.com )BC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,下列结论错误的是
(
)
A.∠C=2∠A
B.BD平分∠ABC
C.S△BCD=S△BOD
D.图中有3个等腰三角形
( http: / / www.21cnjy.com )
3.如图,在△ABC中,点D,E,F分别在
( http: / / www.21cnjy.com )边BC,AB,AC上,且BD=BE,CD=CF,∠A=70°,那么∠FDE等于
(
)
A.40°
B.45°
C.55°
D.60°
4.(2014·茂名)
如图,地面上有三个
( http: / / www.21cnjy.com )洞口A,B,C,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及三个洞口
(到A,B,C三个点的距离相等),尽快抓到老鼠,应该蹲守在
(
)
A.△ABC三边垂直平分线的交点
B.△ABC三条角平分线的交点
C.△ABC三条高所在直线的交点
D.△ABC三条中线的交点
5.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=5,BC=8,则△EFM的周长是
(
)
A.21
B.18
C.13
D
15
( http: / / www.21cnjy.com )
6.如图,在△ABC中,A
( http: / / www.21cnjy.com )B=AC,∠A=36°,BD,CE分别是△ABC,△BCD的角平分线,则图中的等腰三角形有
(
)
A.5个
B.4个
C.3个
D.2个
7.如图,∠MON=30°,点A1,A
( http: / / www.21cnjy.com )2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=1,则△A6
B6
A7的边长为
(
)
二、认真填一填.(每空4分,共28分)
8.(2014·宿迁)
如图,将一
( http: / / www.21cnjy.com )张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C',D'处,C'E交AF于点G,若∠CEF=70°,则∠GFD'=
°.
9.已知等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为40°,此等腰三角形的顶角的度数为
.
10.如图,在△ABC中,AB=AC,BD为∠ABC的平分线,若∠CDB=120°,则∠A=
.
( http: / / www.21cnjy.com )
11.如图,在△ABC中,∠C=90°,AB的垂直平分线分别交BC,AB于点D,E.
(1)
若∠CAB=50°,则∠DAB=
;
(2)
若∠CAD=20°,则∠B=
;
(3)
若∠CAD与∠DAB的度数之比为1:2,则∠B=
.
12.等腰三角形一腰上的中线将这个等腰三角形的周长分成9和12两部分,则腰长为
.
三、耐心解一解.(每题6分,共24分)
13.(2014·襄阳)
如图,在
( http: / / www.21cnjy.com )△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②
BE=CD;③
OB=OC.
(1)
上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形
(用序号写出所有成立的情形)
(2)
请选择(1)中的一种情形,写出证明过程.
( http: / / www.21cnjy.com )
14.如图,在△ABC中,∠BAC=90°,
( http: / / www.21cnjy.com )AB=AC,AE是过A的一条直线,且B,C在AE的两侧,D在A,E之间,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
( http: / / www.21cnjy.com )
15.如图,在四边形ABCD中,∠ABC=∠ADC=90°,M,N分别是AC,BD的中点,判断:MN与BD的位置关系,并说明理由.
( http: / / www.21cnjy.com )
16.如图,P是等边△ABC内的一点,连接PA,PB,PC,以BP为边作等边△BPM,连接CM.
(1)
观察并猜想AP与CM之间的大小关系,并说明你的理由;
(2)
若∠APC=100°,
△PMC为直角三角形,求.∠BPC的度数.
( http: / / www.21cnjy.com )
拓展提优
17.(本题8分)
(1)
如图(1)
( http: / / www.21cnjy.com ),O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小;
(2)
如图(2),△O
( http: / / www.21cnjy.com )AB固定不动,保持△OCD的形状和大小不变,将△OCD绕着点O旋转(△OAB和△OCD不能重叠).求∠AEB的大小.
( http: / / www.21cnjy.com )
18.(本题12分)
(2014·东营)
(1)
如图①,已知:在△AB
( http: / / www.21cnjy.com )C中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E证明:DE=BD+CE.
(2)
如图②,将(1)中的条
( http: / / www.21cnjy.com )件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立
如成立,请你给出证明;若不成立,请说明理由.
(3)
拓展与应用:如图③
( http: / / www.21cnjy.com ),D,E是D,A,E三点所在直线m上的两动点(D,A,E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
( http: / / www.21cnjy.com )
阶段测试(二)
1.C
2.C
3.C
4.A
5.C
6.A
7.C
8.40°
9.50或130°
10.100°
11.40°
35°
( http: / / www.21cnjy.com )36°
12.6或8
13.略
14.∵∠CAE+∠BAD=90°,∠BAD+∠ABD=90°,∴∠CAE=∠ABD.∵∠ADB=∠AEC=90°,AB=AC,∴△ABD≌△CAE.∴AD=CE,BD=AE.∵AE=AD+DE=CE+DE,∴BD=DE+CE
15.MN垂直平分BD
提示:连接BM,DM,证BM=AC,DM=AC,则BM=DM,再用三线合一证MN垂直平分BD.
16.(1)
AP=CM,证△ABP≌△CBM
(2)
110°或150°
17.略
18.证明:(1)
∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=90°.∵∠BAC=90°,∴∠BAD+∠CAE=90°.∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD.
又AB=AC,∴△ADB≌△CEA.∴AE=BD,AD=CE.∴DE=AE+AD=BD+CE.
(2)
∵∠B=∠BAC
=α,∴∠DBA+∠BAD=
∠BAD+∠CAE=180°-α.
( http: / / www.21cnjy.com )∴∠DBA=∠CAE.∵∠BDA=∠AEC=α,AB=AC.∴△ADB≌△CEA.∴AE=BD,AD=CE.∴DE=AE+AD=BD+CE
(3)由(2)知,△ADB≌△CEA,BD=AE,∠DBA=∠CAE.∵△ABF和△ACF均为等边三角形,∴∠ABF=∠CAF=60°.∴∠DBA+
∠ABF=∠CAE+∠CAF.∴∠DB
( http: / / www.21cnjy.com )F=∠FAE.∵BF=AF,∴△DBF≌△EAF.∴DF=EF,∠BFD=∠AFE.∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°.∴△DEF为等边三角形.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
