数学:《导数及其应用》(文)水平测试(二)
文档属性
| 名称 | 数学:《导数及其应用》(文)水平测试(二) |  | |
| 格式 | zip | ||
| 文件大小 | 124.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-26 15:37:00 | ||
图片预览

文档简介
高中数学《导数及其应用》(文)水平测试(二)
一、选择题
1.设在上函数的图象是连续的,且,则下列关系成立的是( )
A. B. C. D.
C
2.曲线在原点处的切线方程为( )
A. B. C. D.
D
3.已知函数,表示的曲线过原点,且在处的切线斜率均为,给出以下结论:
①的解析式为,;
②的极值点有且仅有一个;
③的最大值与最小值之和等于;
其中正确的结论有( )
A.个 B.个 C.个 D.个
C
4.函数( )
A.在区间上是单调增函数
B.在区间上是单调减函数
C.在上是减函数,在上是增函数
D.在上是增函数,在上是减函数
C
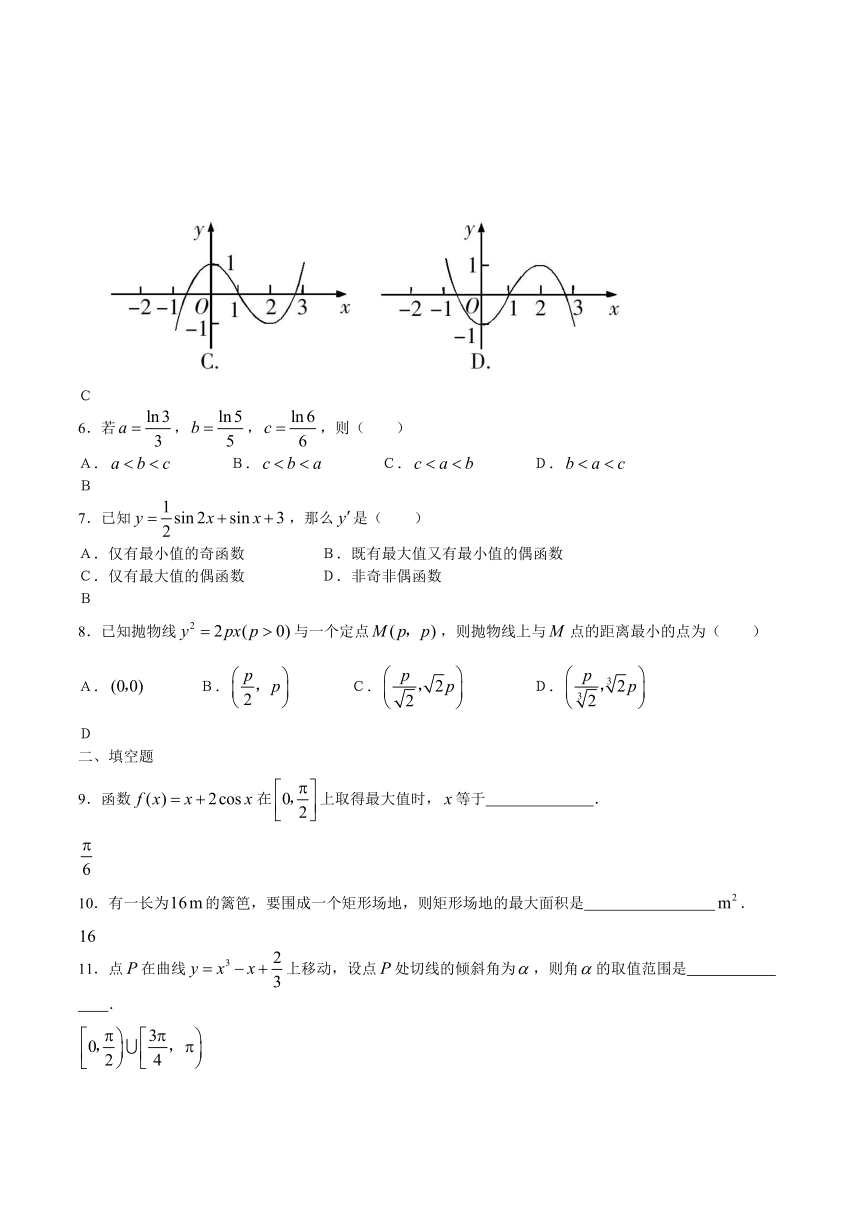
5.设是函数的导函数,的图象如图1所示,则的图象最有可能是( )
C
6.若,,,则( )
A. B. C. D.
B
7.已知,那么是( )
A.仅有最小值的奇函数 B.既有最大值又有最小值的偶函数
C.仅有最大值的偶函数 D.非奇非偶函数
B
8.已知抛物线与一个定点,则抛物线上与点的距离最小的点为( )
A. B. C. D.
D
二、填空题
9.函数在上取得最大值时,等于 .
10.有一长为的篱笆,要围成一个矩形场地,则矩形场地的最大面积是 .
11.点在曲线上移动,设点处切线的倾斜角为,则角的取值范围是 .
12.垂直于直线且与曲线相切的直线方程为 .
13.函数的单调递减区间为 ,递增区间为 .
或
14.已知函数既有极大值又有极小值,则实数的取值范围是 .
或
15.设是二次函数,方程有两个相等实根且,则的表达式是 .
16.已知原命题:“在上可导,且,对于任意实数,如果,则”和该命题的逆命题、否命题、逆否命题,这四个命题中正确的命题个数为 .
三、解答题
17.已知函数与在区间上都是减函数,试确定函数的单调区间.
时,函数为增函数;
或者时,函数为减函数.
18.设函数,已知不论为何实数,恒有且,且方程有三个根.
(1)求的值;
(2)求证:,且;
(3)求的取值范围.
(1);
(2)略;
(3).
19.已知在上单调递增,记的三内角的对应边分别为,若时,不等式恒成立.
(1)求实数的取值范围;
(2)求角的取值范围;
(3)求实数的取值范围.
(1);
(2);
(3).
20.如图2,已知曲线与曲线交于点,,直线与曲线,分别相交于点.
(1)写出四边形的面积与的函数关系式;
(2)讨论的单调性,并求的最大值.
(1);
(2)在区间上是增函数;在区间上是减函数.
的最大值为.
21.某工厂生产某种产品,已知该产品的月生产量与每吨产品的价格(元/)之间的关系式为:,且生产的成本为:(元).问该产品每月生产多少吨才能使利润达到最大?最大利润是多少?(利润=收入-成本)
每月生产才能使利润达到最大,最大利润是元.
一、选择题
1.设在上函数的图象是连续的,且,则下列关系成立的是( )
A. B. C. D.
C
2.曲线在原点处的切线方程为( )
A. B. C. D.
D
3.已知函数,表示的曲线过原点,且在处的切线斜率均为,给出以下结论:
①的解析式为,;
②的极值点有且仅有一个;
③的最大值与最小值之和等于;
其中正确的结论有( )
A.个 B.个 C.个 D.个
C
4.函数( )
A.在区间上是单调增函数
B.在区间上是单调减函数
C.在上是减函数,在上是增函数
D.在上是增函数,在上是减函数
C
5.设是函数的导函数,的图象如图1所示,则的图象最有可能是( )
C
6.若,,,则( )
A. B. C. D.
B
7.已知,那么是( )
A.仅有最小值的奇函数 B.既有最大值又有最小值的偶函数
C.仅有最大值的偶函数 D.非奇非偶函数
B
8.已知抛物线与一个定点,则抛物线上与点的距离最小的点为( )
A. B. C. D.
D
二、填空题
9.函数在上取得最大值时,等于 .
10.有一长为的篱笆,要围成一个矩形场地,则矩形场地的最大面积是 .
11.点在曲线上移动,设点处切线的倾斜角为,则角的取值范围是 .
12.垂直于直线且与曲线相切的直线方程为 .
13.函数的单调递减区间为 ,递增区间为 .
或
14.已知函数既有极大值又有极小值,则实数的取值范围是 .
或
15.设是二次函数,方程有两个相等实根且,则的表达式是 .
16.已知原命题:“在上可导,且,对于任意实数,如果,则”和该命题的逆命题、否命题、逆否命题,这四个命题中正确的命题个数为 .
三、解答题
17.已知函数与在区间上都是减函数,试确定函数的单调区间.
时,函数为增函数;
或者时,函数为减函数.
18.设函数,已知不论为何实数,恒有且,且方程有三个根.
(1)求的值;
(2)求证:,且;
(3)求的取值范围.
(1);
(2)略;
(3).
19.已知在上单调递增,记的三内角的对应边分别为,若时,不等式恒成立.
(1)求实数的取值范围;
(2)求角的取值范围;
(3)求实数的取值范围.
(1);
(2);
(3).
20.如图2,已知曲线与曲线交于点,,直线与曲线,分别相交于点.
(1)写出四边形的面积与的函数关系式;
(2)讨论的单调性,并求的最大值.
(1);
(2)在区间上是增函数;在区间上是减函数.
的最大值为.
21.某工厂生产某种产品,已知该产品的月生产量与每吨产品的价格(元/)之间的关系式为:,且生产的成本为:(元).问该产品每月生产多少吨才能使利润达到最大?最大利润是多少?(利润=收入-成本)
每月生产才能使利润达到最大,最大利润是元.
同课章节目录
