第二十章 数据的分析 全章学案
文档属性
| 名称 | 第二十章 数据的分析 全章学案 |

|
|
| 格式 | doc | ||
| 文件大小 | 186.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-28 00:00:00 | ||
图片预览




文档简介
第二十章 数据的分析
20.1.1平均数(1)
学习目标
1、使学生理解数据的权和加权平均数的概念
2、使学生掌握加权平均数的计算方法
3、通过本节课的学习,还应使学生理解平均数在数据统计中的意义和作用:描述一组数据集中趋势的特征数字,是反映一组数据平均水平的特征数。
重、难点:
1、重点:会求加权平均数
2、难点:对“权”的理解
学习过程
课前准备
1、算术平均数的定义:
一般地,对于n个数x1,x2,…,xn,我们把叫做这n个数的算术平均数(mean),简称平均数,记为,读作“x拔”.
小明经过认真的观察,对上海东方大鲨鱼队队员的年龄总结如下:
年龄/岁 16 18 21 23 24 26 29 34
相应队员数 1 2 4 1 3 1 2 1
计算该队的平均年龄?
2、某广告公司欲招聘广告策划人员一名,对A、B、C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
测试项目 测试成绩
A B C
创新 72 85 67
综合知识 50 74 70
语言 88 45 67
(1)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用?
(2)根据实际需要,公司将创新、综合知识和语言三项测试得分按4:3:1的比例确定各人的测试成绩,此时谁将被录用?
加权平均数的概念
在实际问题中,一组数据的各个数据的“重要程度”未必相同.因而,在计算这组数据的平均数时,往往给每个数据一个“权”.如例1中4、3、1分别是创新、综合知识、语言三项测试成绩的权(weight),而称为A的三项测试成绩的加权平均数.
加权平均数小学学过的平均数计算公式作比较看看意义上是否一致?
4、某校八年级二班一次数学测试成绩如下:100分7人,99分5人,98分6人,95分4人,88分5人,85分5人,80分8人,79分2人,78分4人,65分2人,50分2人,试计算全班的平均成绩.
随堂练习:
1、一组数据:40、37、x、64的平均数是53,则x的值是( )
A、67 B、69 C、71 D、72
2、甲、乙、丙三种饼干售价分别为3元、4元、5元,若将甲种10斤、乙种8斤、丙种7斤混到一起,则售价应该定为每斤( )
A、3.88元 B、4.3元 C、8.7元 D、8.8元
3、某次考试A、B、C、D、E五名学生平均分为62分,除A以外四人平均分为60分,则A得分为( )
A、60 B、62 C、70 D、无法确定
4、老师在计算学期总平均分的时候按如下标准:作业占100%、测验占30%、期中占35%、期末考试占35%,小关和小兵的成绩如下表:
学生 作业 测验 期中考试 期末考试
小关 80 75 71 88
小兵 76 80 68 90
求小关和小兵本学期的总平均分?
5、为了鉴定某种灯泡的质量,对其中100只灯泡的使用寿命进行测量,结果如下表:(单位:小时)
寿命 450 550 600 650 700
只数 20 10 30 15 25
求这些灯泡的平均使用寿命?
三、拓展提高:
1、在一个样本中,2出现了x次,3出现了x次,4出现了x次,5出现了x次,则这个样本的平均数为 .
2、某人打靶,有a次打中环,b次打中环,则这个人平均每次中靶 环。
3、一家公司打算招聘一名部门经理,现对甲、乙两名应聘者从笔试、面试、实习成绩三个方面表现进行评分,笔试占总成绩20%、面试占30%、实习成绩占50%,各项成绩如表所示:
应聘者 笔试 面试 实习
甲 85 83 90
乙 80 85 92
试判断谁会被公司录取,为什么?
4、在一次英语口试中,已知50分1人、60分2人、70分5人、90分5人、100分1人,其余为84分。已知该班平均成绩为80分,问该班有多少人?
四、尝试小结:
20.1.1平均数(2)
学习目标:
1、加深对加权平均数的理解
2、会根据频数分布表求加权平均数,从而解决一些实际问题
3、会用计算器求加权平均数的值
重点、难点
1、重点:根据频数分布表求加权平均数
2、难点:根据频数分布表求加权平均数
学习过程
一、课前准备
1、加权平均数公式
2、为什么可以利用组中值代替一组数据中的每个数据的值?
3、某校为了了解学生作课外作业所用时间的情况,对学生作课外作业所用时间进行调查,下表是该校初二某班50名学生某一天做数学课外作业所用时间的情况统计表
(1)、第二组数据的组中值是多少?
所用时间t(分钟) 人数
0<t≤10 4
10<t≤20 6
20<t≤30 14
30<t≤40 13
40<t≤50 9
50<t≤60 4
(2)、求该班学生平均每天做数学作业所用时间
4、某班40名学生身高情况如下图,
请计算该班学生平均身高?
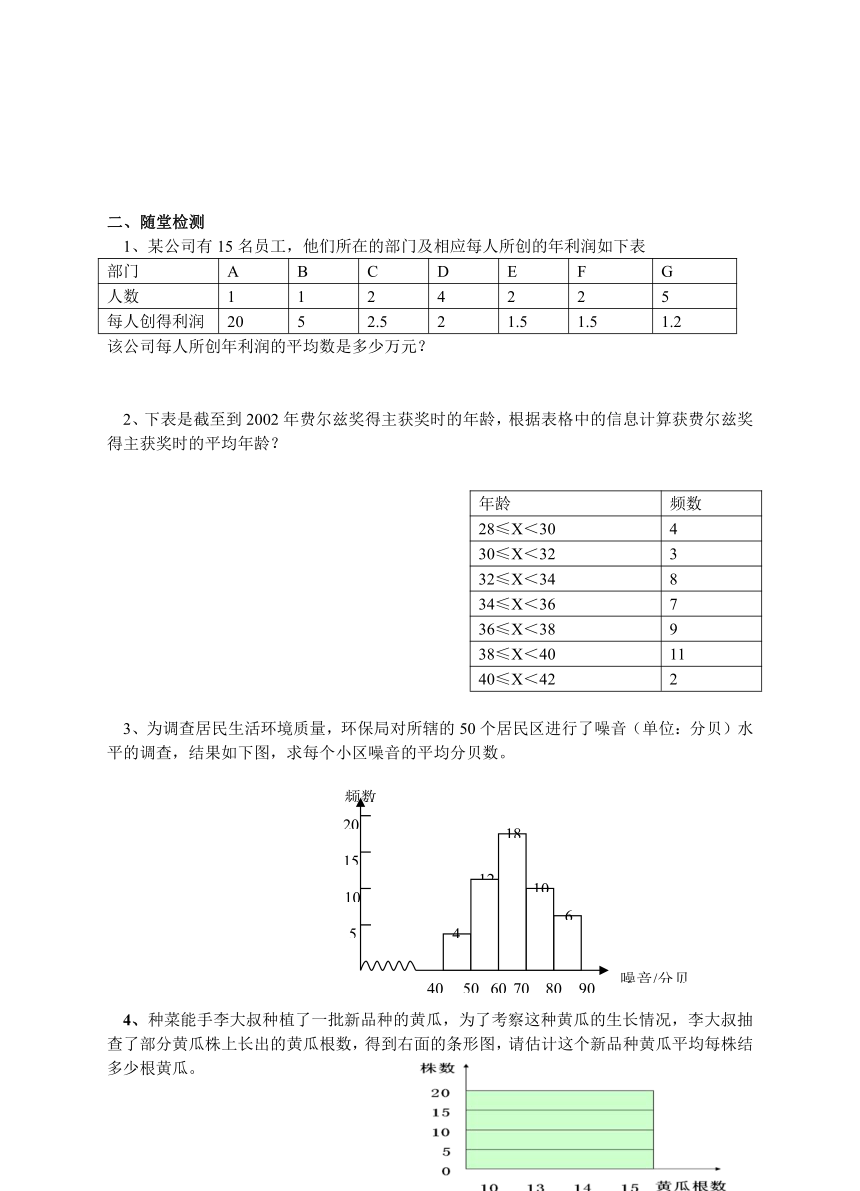
二、随堂检测
1、某公司有15名员工,他们所在的部门及相应每人所创的年利润如下表
部门 A B C D E F G
人数 1 1 2 4 2 2 5
每人创得利润 20 5 2.5 2 1.5 1.5 1.2
该公司每人所创年利润的平均数是多少万元?
2、下表是截至到2002年费尔兹奖得主获奖时的年龄,根据表格中的信息计算获费尔兹奖得主获奖时的平均年龄?
年龄 频数
28≤X<30 4
30≤X<32 3
32≤X<34 8
34≤X<36 7
36≤X<38 9
38≤X<40 11
40≤X<42 2
3、为调查居民生活环境质量,环保局对所辖的50个居民区进行了噪音(单位:分贝)水平的调查,结果如下图,求每个小区噪音的平均分贝数。
4、种菜能手李大叔种植了一批新品种的黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到右面的条形图,请估计这个新品种黄瓜平均每株结多少根黄瓜。
月用水量/吨 10 13 14 17 18
户数 2 2 3 2 1
5、为了解某小区居民的用水情况,随机抽查了该小区10户家庭的月用水量,结果如下表:
(1)求这10户家庭的平均月用水量;
(2)如果该小区有500户家庭,根据上面的计算结果,估计该小区居民每月共用水多少吨?
三、尝试小结
本节我需要重点掌握的解题思想?本节我还存在的疑难问题?
20.1.2中位数和众数(1)
学习目标:
1、认识中位数和众数,并会求出一组数据中的众数和中位数。
2、理解中位数和众数的意义和作用。它们也是数据代表,可以反映一定的数据信息,帮助人们在实际问题中分析并做出决策。
3、会利用中位数、众数分析数据信息做出决策。
重、难点
1、重点:认识中位数、众数这两种数据代表
2、难点:利用中位数、众数分析数据信息做出决策。
学习过程
一、课前准备
1、中位数仅与数据的 有关,某些数据的变动对中位数 影响,中位数可能出现在所给的数据中,当一组数据中的个别数据变动较大时,可用中位数描述其趋势。
众数是当一组数据中某一 出现次数较多时,人们往往关心的一个量,众数不受极端值的影响,这是它的一个优势,中位数的计算很少不受极端值的影响。
2、求中位数的步骤:
⑴、将数据由 排列
⑵、数清数据个数是奇数还是偶数,如果数据个数为奇数则取 ,如果数据个数为偶数,则取中间位置 作为中位数。
求众数的方法:
找出频数 的那个数据,若几个数据频数都是最多且相同,此时众数就是这多个数据。
3、一组数据中出现次数最多的那个数据叫做这组数据的众数.
4、平均数、中位数和众数有哪些特征?
(1)平均数是表示一组数据_______________的一个特征数.
(2)用中位数可以表示一组数据的________________.
(3)用众数可以表示一组数据的__________________.
二、课堂练习
1、某公司销售部有营销人员15人,销售部为了制定某种商品的销售金额,统计了这15个人的销售量如下(单位:件)
1800、510、250、250、210、250、210、210、150、210、150、120、120、210、150
求这15个销售员该月销量的中位数和众数?假设销售部负责人把每位营销员的月销售定额定为320件,你认为合理吗?如果不合理,请你制定一个合理的销售定额并说明理由。
2、某商店3、4月份出售某一品牌各种规格的空调,销售台数如表所示:
根据表格回答问题:
1匹 1.2匹 1.5匹 2匹
3月 12台 20台 8台 4台
4月 16台 30台 14台 8台
商店出售的各种规格空调中,众数是多少?假如你是经理,现要进货,6月份在有限的资金下进货单位将如何决定?
3、某厂生产一批男衬衫,经过抽样调查70名中年男子,得知所需衬衫型号的人如下表所示:
型号(单位:cm) 70 72 74 76 78
人 数 8 12 15 26 9
(1)哪一种型号衬衫的需要量最少 有认认为可以不生产.
(2)这组数据的平均数是多少 是否可按这个型号生产
(3)这组数据的中位数是多少 有人认为这种型号的衬衫产量要占第一位.
(4)这组数据的众数是多少 有人认为这种型号的衬衫产量要占第一位.
4、已知2,4,2x,4y四个数的平均数是5,5,7,4x,6y四个数的平均数是9,求出x2+y2的值以及第一组数据的中位数和第二组数据的众数.
三、拓展提高
数据8、9、9、8、10、8、99、8、10、7、9、9、8的中位数是 ,众数是
一组数据23、27、20、18、X、12,它的中位数是21,则X的值是 .
数据92、96、98、100、X的众数是96,则其中位数和平均数分别是( )
A.97、96 B.96、96.4 C.96、97 D.98、97
如果在一组数据中,23、25、28、22出现的次数依次为2、5、3、4次,并且没有其他的数据,则这组数据的众数和中位数分别是( )
A.24、25 B.23、24 C.25、25 D.23、25
随机抽取我市一年(按365天计)中的30天平均气温状况如下表:
温度(℃) -8 -1 7 15 21 24 30
天数 3 5 5 7 6 2 2
请你根据上述数据回答问题:
(1).该组数据的中位数是什么?
(2).若当气温在18℃~25℃为市民“满意温度”,则我市一年中达到市民“满意温度”的大约有多少天?
6、某公司有15名员工,他们所在的部门及相应每人所创的年利润(万元/人·年)如下表所示:
(1)该公司每人所创年利润的平均数是___________万元,中位数是_________万元,众数是__________万元.
部门 A B C D E F G
人数 1 1 2 4 2 2 3
利润 20 5 2.5 2.1 1.5 1.5 1.2
(2)你认为应该使用平均数还是中位数来描述该公司每人所创年利润的一般水平?
四、尝试小结
20.1.2中位数和众数(2)
学习目标:
1、进一步认识平均数、众数、中位数都是数据的代表。
2、通过本节课的学习还应了解平均数、中位数、众数在描述数据时的差异。
3、能灵活应用这三个数据代表解决实际问题。
重点、难点
1、重点:了解平均数、中位数、众数之间的差异。
2、难点:灵活运用这三个数据代表解决问题。
学习过程
一、课前准备
1、平均数、众数和中位数的定义
2、平均数、中位数和众数都可以作为一组数据的代表,主要描述一组数据集中趋势的量。平均数是应用较多的一种量。
平均数计算要用到所有的数据,它能够充分利用 的数据信息,但它受 .影响大。
众数是当一组数据中某一数据 较多时,人们往往关心的一个量,众数不受极端值的影响,这是它的一个优势,中位数的计算很少也不受 的影响.
中位数仅与数据的 有关,某些数据的移动对中位数没有影响,中位数可能出现在所给数据中也可能不在所给的数据中,当一组数据中的个别数据变动较大时,可用 描述其趋势.
注意:实际问题中求得的平均数,众数,中位数应带上单位.
3、某公司有15名员工,他们所在的部门及相应每人所创的年利润(万元/人·年)如下表所示:
部门 A B C D E F G
人数 1 1 2 4 2 2 3
利润 20 5 2.5 2.1 1.5 1.5 1.2
(1)该公司每人所创年利润的平均数是___________万元,中位数是_________万元,众数是__________万元.
(2)你认为应该使用平均数还是中位数来描述该公司每人所创年利润的一般水平?
随堂练习
1.已知数据x1,x2,…,xn的平均数是,则一组新数据x1+8,x2+8,…,xn+8的平均数是________.
2.若3,4,5,6,a,b,c的平均数为12,则a+b+c=________.
3.某同学参加了5科考试,平均成绩是68分,他想在下一科考试后使6科考试的平均成绩为70分,那么他第6科考试要得的分数应为 ( )
A.72分 B.74分 C.78分 D.80分
4.小华同学为了丰富暑假生活,骑自行车到某景点旅游.开始出发时以20千米/时的速度行驶,1小时后,由于天气情况及体力原因,骑车速度变为15千米/时,这样又行驶了1.5小时到达景点,那么小华去时的平均速度是______千米/时.
5、在一次环保知识竞赛中,某班50名学生成绩如下表所示:
得分 50 60 70 80 90 100 110 120
人数 2 3 6 14 15 5 4 1
分别求出这些学生成绩的众数、中位数和平均数.
6、公园里有甲、乙两群游客正在做团体游戏,两群游客的年龄如下:(单位:岁)
甲群:13、13、14、15、15、15、16、17、17。
乙群:3、4、4、5、5、6、6、54、57。
(1)、甲群游客的平均年龄是 岁,中位数是 岁,众数是 岁,其中能较好反映甲群游客年龄特征的是 。
(2)、乙群游客的平均年龄是 岁,中位数是 岁,众数是 岁。其中能较好反映乙群游客年龄特征的是 。
三、拓展提高
1.若数据10,12,9,-1,4,8,10,12,x的众数是12,则x=__________.
2.把9个数按从小到大的顺序排列,其平均数是9,如果这组数中前5个数的平均数是8,后5个数的平均数是10,则这9个数的中位数是________.
3.用中位数去估计总体时,其优越性是 ( )
A.运算简便 B.不受较大数据的影响 C.不受较小数据的影响 D.不受个别数据较大或较小的影响
4.对于数据3,3,2,6,3,10,3,6,3,2.
(1) 众数是3 (2) 众数与中位数的数值不等 (3) 中位数与平均数的数值相等 (4) 平均数与众数相等
其中正确的结论是 ( )
A.(1) B.(1) (3) C.(2) D.(2) (4)
5、某公司的33名职工的月工资(以元为单位)如下:
职员 董事长 副董事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 5500 5000 3500 3000 2500 2000 1500
(1)、求该公司职员月工资的平均数、中位数、众数?
(2)、假设副董事长的工资从5000元提升到20000元,董事长的工资从5500元提升到30000元,那么新的平均数、中位数、众数又是什么?(精确到元)
(3)、你认为应该使用平均数和中位数中哪一个来描述该公司职工的工资水平?
6、某公司有15名员工,它们所在的部门及相应每人所创的年利润如下表示:
部门 A B C D E F G
人数 1 1 2 4 2 2 3
每人所创的年利润 20 5 2.5 2.1 1.5 1.5 1.2
根据表中的信息填空:
该公司每人所创年利润的平均数是 万元。
该公司每人所创年利润的中位数是 万元。
你认为应该使用平均数和中位数中哪一个来描述该公司每人所创年利润的一般水平?答
四、尝试小结
20.2.1极差
学习目标:
1、理解极差的定义,知道极差是用来反映数据波动范围的一个量
2、会求一组数据的极差
重、难点
会求一组数据的极差。
学习过程
一、课前准备
1、一组数据:473、865、368、774、539、474的极差是 ,
一组数据1736、1350、-2114、-1736的极差是 .
2、一组数据3、-1、0、2、X的极差是5,且X为自然数,则X= .
3、下列几个常见统计量中能够反映一组数据波动范围的是( )
A.平均数 B.中位数 C.众数 D.极差
4、一组数据X、X…X的极差是8,则另一组数据2X+1、2X+1…,2X+1的极差是( )
A. 8 B.16 C.9 D.17
5、样本3,4,2,1,5的平均数为 ;中位数为 ;极差为 ;
样本a+3,a+4,a+2,a+1,a+5的平均数为 中位数为 极差为 。
6、试计算下列两组数据的极差:
A组:0, 10, 5, 5, 5, 5, 5, 5, 5, 5;
B组:4, 6, 3, 7, 2, 8, 1, 9, 5, 5.
二、课堂练习
1、已知样本9.9、10.3、10.3、9.9、10.1,则样本极差是( )
A. 0.4 B.16 C.0.2 D.无法确定
在一次数学考试中,第一小组14名学生的成绩与全组平均分的差是2、3、-5、10、12、8、
2、-1、4、-10、-2、5、5、-5,那么这个小组的平均成绩是( )
A. 87 B. 83 C. 85 D无法确定
3、已知一组数据2.1、1.9、1.8、X、2.2的平均数为2,则极差是 。
4、若10个数的平均数是3,极差是4,则将这10个数都扩大10倍,则这组数据的平均数是 ,极差是 。
5、某活动小组为使全小组成员的成绩都要达到优秀,打算实施“以优帮困”计划,为此统计了上次测试各成员的成绩(单位:分)
90、95、87、92、63、54、82、76、55、100、45、80
计算这组数据的极差,这个极差说明什么问题?将数据适当分组,做出频率分布表和频数分布直方图。
三、拓展提高
1、在数据统计中,能反映一组数据变化范围大小的指标是( )
2、数据 -1 , 3 , 0 , x 的极差是 5 ,则 x =_____
3、某日最高气温是4 ℃, 温差是 9 ℃,则最低气温是___ ℃.
4、数据 0 , -1 , 3 , 2 , 4 的极差是_____
5、在数据:3 、4 、5、 1.5 、9中,中位数是_____,极差是_____.
6、公园有两条石级路,第一条石级路的 高度分别是(单位:cm):15,16,16,14,15,14;第二条石级路的 高度分别是11,15,17,18,19,10,哪条路走起来更舒服?
8:00 12:00 16:00 20:00
23℃ 30℃ 28℃ 25℃
7、我市某天的气温情况如下表:
极差是 。
8、质检部门为了检验两种灯泡的使用寿命,各抽出8只试验,结果如下(单位:小时)
40瓦 457 443 459 451 444 464 460 438
60瓦 466 439 452 464 438 459 467 455
哪种灯泡的使用寿命长?哪种灯泡的质量稳定?
9、我校想派一名跳高运动员参赛,对甲.乙两名跳高运动员进行了 8 次选拔测试,他们的跳高成绩 (单位:m)如下:
甲: 1.70 1.65 1.68 1.72 1.73 1.68 1.67 1.69
乙: 1.60 1.73 1.72 1.61 1.62 1.71 1.70 1.75
(1)甲.乙两名跳高运动员的平均成绩分别是多少
(2)哪个人的成绩更为稳定
(3)经预测,跳高成绩 1.65 m 就可能获得冠军,应选哪位运动员参赛 若预测跳高成绩 超过 1.70 m 就很可能破记录,则选哪位运动员参赛
10、一次八年级数学单元测试,对数学成绩进行考察,从(1)(2)两班中共抽取了 50 人,成绩分别是(满分为 100 分):
88 , 74 , 67 , 49 , 69 , 38 , 86 , 77 , 66 , 75 ,
94 , 67 , 78 , 69 , 84 , 50 , 39 , 58 , 79 , 70 ,
90 , 79 , 97 , 75 . 98 , 77 , 64 , 69 , 82 , 71 ,
65 , 68 , 62 , 73 , 58 , 78 , 75 , 89 , 91 , 99 ,
72 , 62 , 74 , 81 , 79 , 81 , 86 , 78 , 90 , 81
(1)计算这组数据的极差,这个极差说明了什么问题
(2)将数据适当分组,作出频数分布表和频数分布直方图;
(3)这次数学考试的及格率是多少
四、尝试小结
20.2.2 方差
学习目标:
1. 了解方差的定义和计算公式。
2. 理解方差概念的产生和形成的过程。
3. 会用方差计算公式来比较两组数据的波动大小。
重点、难点
1. 重点:方差产生的必要性和应用方差公式解决实际问题。
2. 难点:理解方差公式
学习过程
一、课前准备
1、为什么要学习方差和方差公式?波动性可以通过什么方式表现出来?
方差公式:S= 其中n代表 、代表
2、从甲、乙两种农作物中各抽取1株苗,分别测得它的苗高如下:(单位:cm)
甲:9、10、11、12、7、13、10、8、12、8;
乙:8、13、12、11、10、12、7、7、9、11;
问:(1)哪种农作物的苗长的比较高?
(2)哪种农作物的苗长得比较整齐?
3、 段巍和金志强两人参加体育项目训练,近期的5次测试成绩如下表所示,谁的成绩比较稳定?为什么?
测试次数 1 2 3 4 5
段巍 13 14 13 12 13
金志强 10 13 16 14 12
二、巩固练习
1、已知一组数据为2、0、-1、3、-4,则这组数据的方差为 。
2、甲、乙两名学生在相同的条件下各射靶10次,命中的环数如下:
甲:7、8、6、8、6、5、9、10、7、4
乙:9、5、7、8、7、6、8、6、7、7
经过计算,两人射击环数的平均数相同,但S S,所以确定 去参加比赛。
3、甲、乙两台机床生产同种零件,10天出的次品分别是:
甲:0、1、0、2、2、0、3、1、2、4
乙:2、3、1、2、0、2、1、1、2、1
分别计算出两个样本的平均数和方差,根据你的计算判断哪台机床的性能较好?
4、在一次芭蕾舞的比赛中,甲乙两个芭蕾舞团都表演了舞剧(天鹅湖),参加表演的女演员的身高(单位:cm)分别是
甲团: 163 164 164 165 165 165 166 167
乙团: 163 164 164 165 166 167 167 168
哪个芭蕾舞团的女演员的身高更整齐?
5、小爽和小兵在10次百米跑步练习中成绩如表所示:(单位:秒)
小爽 10.8 10.9 11.0 10.7 11.1 11.1 10.8 11.0 10.7 10.9
小兵 10.9 10.9 10.8 10.8 11.0 10.9 10.8 11.1 10.9 10.8
如果根据这几次成绩选拔一人参加比赛,你会选谁呢?
拓展提高
1、样本为101,98,102,100,99的极差是 , 方差是 .
2、甲、乙两个样本,甲样本方差是2.15,乙样本
方差是2.31,则甲样本和乙样本的离散程度( )
A.甲、乙离散程度一样
B.甲比乙的离散程度大
C.乙比甲的离散程度大
D.无法比较
3、甲、乙两名学生在参加今年体育考试前各做了5次立定跳远测试,两人的平均成绩相同,其中甲所测得成绩的方差是0.005,乙所测得的成绩如下:2.20 m,2.30 m,2.30 m,2.40 m,2.30 m,那么甲、乙的成绩比较( )
A.甲的成绩更稳定 B.乙的成绩更稳定
C.甲、乙的成绩一样稳定 D.不能确定谁的成绩更稳定
4、学校准备进一批新的课桌椅,现有两个厂家的课桌椅质量、价格均相同,按规定,中学生的课桌高度应为70cm,椅子应为40cm左右,学校分别从两个厂家随机选了5套桌椅,测得高度(单位:cm)如下:
甲厂课桌:72 69 70 71 69
甲厂椅子:39 40 40 41 41
乙厂课桌:68 71 72 70 69
乙厂椅子:42 41 39 40 39
你认为学校应该买哪家的课桌椅?
5、某农民几年前承包了甲、乙两片荒山,各栽了100棵蜜橘,成活98%,现已挂果,经济效益显著,为了分析经营情况,他从甲山随意采摘了3棵树上的蜜橘称得质量分别为25,18,20千克;他从乙山随意采摘了4棵树上的蜜橘,称得质量分别为21,24,20千克。
组成一个样本,问:
(1)样本容量是多少?
(2)样本平均数是多少?并估算出甲、乙两山蜜橘的总产量?
(3)甲、乙两山哪个山上蜜橘长势较整齐?
四、尝试小结
165
10
5
身高(cm)
185
175
155
145
15
20
6
10
20
4
人数(人)
60
10
5
噪音/分贝
80
70
50
40
15
20
6
12
18
4
频数
10
90
台数
规格
月份
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
20.1.1平均数(1)
学习目标
1、使学生理解数据的权和加权平均数的概念
2、使学生掌握加权平均数的计算方法
3、通过本节课的学习,还应使学生理解平均数在数据统计中的意义和作用:描述一组数据集中趋势的特征数字,是反映一组数据平均水平的特征数。
重、难点:
1、重点:会求加权平均数
2、难点:对“权”的理解
学习过程
课前准备
1、算术平均数的定义:
一般地,对于n个数x1,x2,…,xn,我们把叫做这n个数的算术平均数(mean),简称平均数,记为,读作“x拔”.
小明经过认真的观察,对上海东方大鲨鱼队队员的年龄总结如下:
年龄/岁 16 18 21 23 24 26 29 34
相应队员数 1 2 4 1 3 1 2 1
计算该队的平均年龄?
2、某广告公司欲招聘广告策划人员一名,对A、B、C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
测试项目 测试成绩
A B C
创新 72 85 67
综合知识 50 74 70
语言 88 45 67
(1)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用?
(2)根据实际需要,公司将创新、综合知识和语言三项测试得分按4:3:1的比例确定各人的测试成绩,此时谁将被录用?
加权平均数的概念
在实际问题中,一组数据的各个数据的“重要程度”未必相同.因而,在计算这组数据的平均数时,往往给每个数据一个“权”.如例1中4、3、1分别是创新、综合知识、语言三项测试成绩的权(weight),而称为A的三项测试成绩的加权平均数.
加权平均数小学学过的平均数计算公式作比较看看意义上是否一致?
4、某校八年级二班一次数学测试成绩如下:100分7人,99分5人,98分6人,95分4人,88分5人,85分5人,80分8人,79分2人,78分4人,65分2人,50分2人,试计算全班的平均成绩.
随堂练习:
1、一组数据:40、37、x、64的平均数是53,则x的值是( )
A、67 B、69 C、71 D、72
2、甲、乙、丙三种饼干售价分别为3元、4元、5元,若将甲种10斤、乙种8斤、丙种7斤混到一起,则售价应该定为每斤( )
A、3.88元 B、4.3元 C、8.7元 D、8.8元
3、某次考试A、B、C、D、E五名学生平均分为62分,除A以外四人平均分为60分,则A得分为( )
A、60 B、62 C、70 D、无法确定
4、老师在计算学期总平均分的时候按如下标准:作业占100%、测验占30%、期中占35%、期末考试占35%,小关和小兵的成绩如下表:
学生 作业 测验 期中考试 期末考试
小关 80 75 71 88
小兵 76 80 68 90
求小关和小兵本学期的总平均分?
5、为了鉴定某种灯泡的质量,对其中100只灯泡的使用寿命进行测量,结果如下表:(单位:小时)
寿命 450 550 600 650 700
只数 20 10 30 15 25
求这些灯泡的平均使用寿命?
三、拓展提高:
1、在一个样本中,2出现了x次,3出现了x次,4出现了x次,5出现了x次,则这个样本的平均数为 .
2、某人打靶,有a次打中环,b次打中环,则这个人平均每次中靶 环。
3、一家公司打算招聘一名部门经理,现对甲、乙两名应聘者从笔试、面试、实习成绩三个方面表现进行评分,笔试占总成绩20%、面试占30%、实习成绩占50%,各项成绩如表所示:
应聘者 笔试 面试 实习
甲 85 83 90
乙 80 85 92
试判断谁会被公司录取,为什么?
4、在一次英语口试中,已知50分1人、60分2人、70分5人、90分5人、100分1人,其余为84分。已知该班平均成绩为80分,问该班有多少人?
四、尝试小结:
20.1.1平均数(2)
学习目标:
1、加深对加权平均数的理解
2、会根据频数分布表求加权平均数,从而解决一些实际问题
3、会用计算器求加权平均数的值
重点、难点
1、重点:根据频数分布表求加权平均数
2、难点:根据频数分布表求加权平均数
学习过程
一、课前准备
1、加权平均数公式
2、为什么可以利用组中值代替一组数据中的每个数据的值?
3、某校为了了解学生作课外作业所用时间的情况,对学生作课外作业所用时间进行调查,下表是该校初二某班50名学生某一天做数学课外作业所用时间的情况统计表
(1)、第二组数据的组中值是多少?
所用时间t(分钟) 人数
0<t≤10 4
10<t≤20 6
20<t≤30 14
30<t≤40 13
40<t≤50 9
50<t≤60 4
(2)、求该班学生平均每天做数学作业所用时间
4、某班40名学生身高情况如下图,
请计算该班学生平均身高?
二、随堂检测
1、某公司有15名员工,他们所在的部门及相应每人所创的年利润如下表
部门 A B C D E F G
人数 1 1 2 4 2 2 5
每人创得利润 20 5 2.5 2 1.5 1.5 1.2
该公司每人所创年利润的平均数是多少万元?
2、下表是截至到2002年费尔兹奖得主获奖时的年龄,根据表格中的信息计算获费尔兹奖得主获奖时的平均年龄?
年龄 频数
28≤X<30 4
30≤X<32 3
32≤X<34 8
34≤X<36 7
36≤X<38 9
38≤X<40 11
40≤X<42 2
3、为调查居民生活环境质量,环保局对所辖的50个居民区进行了噪音(单位:分贝)水平的调查,结果如下图,求每个小区噪音的平均分贝数。
4、种菜能手李大叔种植了一批新品种的黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到右面的条形图,请估计这个新品种黄瓜平均每株结多少根黄瓜。
月用水量/吨 10 13 14 17 18
户数 2 2 3 2 1
5、为了解某小区居民的用水情况,随机抽查了该小区10户家庭的月用水量,结果如下表:
(1)求这10户家庭的平均月用水量;
(2)如果该小区有500户家庭,根据上面的计算结果,估计该小区居民每月共用水多少吨?
三、尝试小结
本节我需要重点掌握的解题思想?本节我还存在的疑难问题?
20.1.2中位数和众数(1)
学习目标:
1、认识中位数和众数,并会求出一组数据中的众数和中位数。
2、理解中位数和众数的意义和作用。它们也是数据代表,可以反映一定的数据信息,帮助人们在实际问题中分析并做出决策。
3、会利用中位数、众数分析数据信息做出决策。
重、难点
1、重点:认识中位数、众数这两种数据代表
2、难点:利用中位数、众数分析数据信息做出决策。
学习过程
一、课前准备
1、中位数仅与数据的 有关,某些数据的变动对中位数 影响,中位数可能出现在所给的数据中,当一组数据中的个别数据变动较大时,可用中位数描述其趋势。
众数是当一组数据中某一 出现次数较多时,人们往往关心的一个量,众数不受极端值的影响,这是它的一个优势,中位数的计算很少不受极端值的影响。
2、求中位数的步骤:
⑴、将数据由 排列
⑵、数清数据个数是奇数还是偶数,如果数据个数为奇数则取 ,如果数据个数为偶数,则取中间位置 作为中位数。
求众数的方法:
找出频数 的那个数据,若几个数据频数都是最多且相同,此时众数就是这多个数据。
3、一组数据中出现次数最多的那个数据叫做这组数据的众数.
4、平均数、中位数和众数有哪些特征?
(1)平均数是表示一组数据_______________的一个特征数.
(2)用中位数可以表示一组数据的________________.
(3)用众数可以表示一组数据的__________________.
二、课堂练习
1、某公司销售部有营销人员15人,销售部为了制定某种商品的销售金额,统计了这15个人的销售量如下(单位:件)
1800、510、250、250、210、250、210、210、150、210、150、120、120、210、150
求这15个销售员该月销量的中位数和众数?假设销售部负责人把每位营销员的月销售定额定为320件,你认为合理吗?如果不合理,请你制定一个合理的销售定额并说明理由。
2、某商店3、4月份出售某一品牌各种规格的空调,销售台数如表所示:
根据表格回答问题:
1匹 1.2匹 1.5匹 2匹
3月 12台 20台 8台 4台
4月 16台 30台 14台 8台
商店出售的各种规格空调中,众数是多少?假如你是经理,现要进货,6月份在有限的资金下进货单位将如何决定?
3、某厂生产一批男衬衫,经过抽样调查70名中年男子,得知所需衬衫型号的人如下表所示:
型号(单位:cm) 70 72 74 76 78
人 数 8 12 15 26 9
(1)哪一种型号衬衫的需要量最少 有认认为可以不生产.
(2)这组数据的平均数是多少 是否可按这个型号生产
(3)这组数据的中位数是多少 有人认为这种型号的衬衫产量要占第一位.
(4)这组数据的众数是多少 有人认为这种型号的衬衫产量要占第一位.
4、已知2,4,2x,4y四个数的平均数是5,5,7,4x,6y四个数的平均数是9,求出x2+y2的值以及第一组数据的中位数和第二组数据的众数.
三、拓展提高
数据8、9、9、8、10、8、99、8、10、7、9、9、8的中位数是 ,众数是
一组数据23、27、20、18、X、12,它的中位数是21,则X的值是 .
数据92、96、98、100、X的众数是96,则其中位数和平均数分别是( )
A.97、96 B.96、96.4 C.96、97 D.98、97
如果在一组数据中,23、25、28、22出现的次数依次为2、5、3、4次,并且没有其他的数据,则这组数据的众数和中位数分别是( )
A.24、25 B.23、24 C.25、25 D.23、25
随机抽取我市一年(按365天计)中的30天平均气温状况如下表:
温度(℃) -8 -1 7 15 21 24 30
天数 3 5 5 7 6 2 2
请你根据上述数据回答问题:
(1).该组数据的中位数是什么?
(2).若当气温在18℃~25℃为市民“满意温度”,则我市一年中达到市民“满意温度”的大约有多少天?
6、某公司有15名员工,他们所在的部门及相应每人所创的年利润(万元/人·年)如下表所示:
(1)该公司每人所创年利润的平均数是___________万元,中位数是_________万元,众数是__________万元.
部门 A B C D E F G
人数 1 1 2 4 2 2 3
利润 20 5 2.5 2.1 1.5 1.5 1.2
(2)你认为应该使用平均数还是中位数来描述该公司每人所创年利润的一般水平?
四、尝试小结
20.1.2中位数和众数(2)
学习目标:
1、进一步认识平均数、众数、中位数都是数据的代表。
2、通过本节课的学习还应了解平均数、中位数、众数在描述数据时的差异。
3、能灵活应用这三个数据代表解决实际问题。
重点、难点
1、重点:了解平均数、中位数、众数之间的差异。
2、难点:灵活运用这三个数据代表解决问题。
学习过程
一、课前准备
1、平均数、众数和中位数的定义
2、平均数、中位数和众数都可以作为一组数据的代表,主要描述一组数据集中趋势的量。平均数是应用较多的一种量。
平均数计算要用到所有的数据,它能够充分利用 的数据信息,但它受 .影响大。
众数是当一组数据中某一数据 较多时,人们往往关心的一个量,众数不受极端值的影响,这是它的一个优势,中位数的计算很少也不受 的影响.
中位数仅与数据的 有关,某些数据的移动对中位数没有影响,中位数可能出现在所给数据中也可能不在所给的数据中,当一组数据中的个别数据变动较大时,可用 描述其趋势.
注意:实际问题中求得的平均数,众数,中位数应带上单位.
3、某公司有15名员工,他们所在的部门及相应每人所创的年利润(万元/人·年)如下表所示:
部门 A B C D E F G
人数 1 1 2 4 2 2 3
利润 20 5 2.5 2.1 1.5 1.5 1.2
(1)该公司每人所创年利润的平均数是___________万元,中位数是_________万元,众数是__________万元.
(2)你认为应该使用平均数还是中位数来描述该公司每人所创年利润的一般水平?
随堂练习
1.已知数据x1,x2,…,xn的平均数是,则一组新数据x1+8,x2+8,…,xn+8的平均数是________.
2.若3,4,5,6,a,b,c的平均数为12,则a+b+c=________.
3.某同学参加了5科考试,平均成绩是68分,他想在下一科考试后使6科考试的平均成绩为70分,那么他第6科考试要得的分数应为 ( )
A.72分 B.74分 C.78分 D.80分
4.小华同学为了丰富暑假生活,骑自行车到某景点旅游.开始出发时以20千米/时的速度行驶,1小时后,由于天气情况及体力原因,骑车速度变为15千米/时,这样又行驶了1.5小时到达景点,那么小华去时的平均速度是______千米/时.
5、在一次环保知识竞赛中,某班50名学生成绩如下表所示:
得分 50 60 70 80 90 100 110 120
人数 2 3 6 14 15 5 4 1
分别求出这些学生成绩的众数、中位数和平均数.
6、公园里有甲、乙两群游客正在做团体游戏,两群游客的年龄如下:(单位:岁)
甲群:13、13、14、15、15、15、16、17、17。
乙群:3、4、4、5、5、6、6、54、57。
(1)、甲群游客的平均年龄是 岁,中位数是 岁,众数是 岁,其中能较好反映甲群游客年龄特征的是 。
(2)、乙群游客的平均年龄是 岁,中位数是 岁,众数是 岁。其中能较好反映乙群游客年龄特征的是 。
三、拓展提高
1.若数据10,12,9,-1,4,8,10,12,x的众数是12,则x=__________.
2.把9个数按从小到大的顺序排列,其平均数是9,如果这组数中前5个数的平均数是8,后5个数的平均数是10,则这9个数的中位数是________.
3.用中位数去估计总体时,其优越性是 ( )
A.运算简便 B.不受较大数据的影响 C.不受较小数据的影响 D.不受个别数据较大或较小的影响
4.对于数据3,3,2,6,3,10,3,6,3,2.
(1) 众数是3 (2) 众数与中位数的数值不等 (3) 中位数与平均数的数值相等 (4) 平均数与众数相等
其中正确的结论是 ( )
A.(1) B.(1) (3) C.(2) D.(2) (4)
5、某公司的33名职工的月工资(以元为单位)如下:
职员 董事长 副董事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 5500 5000 3500 3000 2500 2000 1500
(1)、求该公司职员月工资的平均数、中位数、众数?
(2)、假设副董事长的工资从5000元提升到20000元,董事长的工资从5500元提升到30000元,那么新的平均数、中位数、众数又是什么?(精确到元)
(3)、你认为应该使用平均数和中位数中哪一个来描述该公司职工的工资水平?
6、某公司有15名员工,它们所在的部门及相应每人所创的年利润如下表示:
部门 A B C D E F G
人数 1 1 2 4 2 2 3
每人所创的年利润 20 5 2.5 2.1 1.5 1.5 1.2
根据表中的信息填空:
该公司每人所创年利润的平均数是 万元。
该公司每人所创年利润的中位数是 万元。
你认为应该使用平均数和中位数中哪一个来描述该公司每人所创年利润的一般水平?答
四、尝试小结
20.2.1极差
学习目标:
1、理解极差的定义,知道极差是用来反映数据波动范围的一个量
2、会求一组数据的极差
重、难点
会求一组数据的极差。
学习过程
一、课前准备
1、一组数据:473、865、368、774、539、474的极差是 ,
一组数据1736、1350、-2114、-1736的极差是 .
2、一组数据3、-1、0、2、X的极差是5,且X为自然数,则X= .
3、下列几个常见统计量中能够反映一组数据波动范围的是( )
A.平均数 B.中位数 C.众数 D.极差
4、一组数据X、X…X的极差是8,则另一组数据2X+1、2X+1…,2X+1的极差是( )
A. 8 B.16 C.9 D.17
5、样本3,4,2,1,5的平均数为 ;中位数为 ;极差为 ;
样本a+3,a+4,a+2,a+1,a+5的平均数为 中位数为 极差为 。
6、试计算下列两组数据的极差:
A组:0, 10, 5, 5, 5, 5, 5, 5, 5, 5;
B组:4, 6, 3, 7, 2, 8, 1, 9, 5, 5.
二、课堂练习
1、已知样本9.9、10.3、10.3、9.9、10.1,则样本极差是( )
A. 0.4 B.16 C.0.2 D.无法确定
在一次数学考试中,第一小组14名学生的成绩与全组平均分的差是2、3、-5、10、12、8、
2、-1、4、-10、-2、5、5、-5,那么这个小组的平均成绩是( )
A. 87 B. 83 C. 85 D无法确定
3、已知一组数据2.1、1.9、1.8、X、2.2的平均数为2,则极差是 。
4、若10个数的平均数是3,极差是4,则将这10个数都扩大10倍,则这组数据的平均数是 ,极差是 。
5、某活动小组为使全小组成员的成绩都要达到优秀,打算实施“以优帮困”计划,为此统计了上次测试各成员的成绩(单位:分)
90、95、87、92、63、54、82、76、55、100、45、80
计算这组数据的极差,这个极差说明什么问题?将数据适当分组,做出频率分布表和频数分布直方图。
三、拓展提高
1、在数据统计中,能反映一组数据变化范围大小的指标是( )
2、数据 -1 , 3 , 0 , x 的极差是 5 ,则 x =_____
3、某日最高气温是4 ℃, 温差是 9 ℃,则最低气温是___ ℃.
4、数据 0 , -1 , 3 , 2 , 4 的极差是_____
5、在数据:3 、4 、5、 1.5 、9中,中位数是_____,极差是_____.
6、公园有两条石级路,第一条石级路的 高度分别是(单位:cm):15,16,16,14,15,14;第二条石级路的 高度分别是11,15,17,18,19,10,哪条路走起来更舒服?
8:00 12:00 16:00 20:00
23℃ 30℃ 28℃ 25℃
7、我市某天的气温情况如下表:
极差是 。
8、质检部门为了检验两种灯泡的使用寿命,各抽出8只试验,结果如下(单位:小时)
40瓦 457 443 459 451 444 464 460 438
60瓦 466 439 452 464 438 459 467 455
哪种灯泡的使用寿命长?哪种灯泡的质量稳定?
9、我校想派一名跳高运动员参赛,对甲.乙两名跳高运动员进行了 8 次选拔测试,他们的跳高成绩 (单位:m)如下:
甲: 1.70 1.65 1.68 1.72 1.73 1.68 1.67 1.69
乙: 1.60 1.73 1.72 1.61 1.62 1.71 1.70 1.75
(1)甲.乙两名跳高运动员的平均成绩分别是多少
(2)哪个人的成绩更为稳定
(3)经预测,跳高成绩 1.65 m 就可能获得冠军,应选哪位运动员参赛 若预测跳高成绩 超过 1.70 m 就很可能破记录,则选哪位运动员参赛
10、一次八年级数学单元测试,对数学成绩进行考察,从(1)(2)两班中共抽取了 50 人,成绩分别是(满分为 100 分):
88 , 74 , 67 , 49 , 69 , 38 , 86 , 77 , 66 , 75 ,
94 , 67 , 78 , 69 , 84 , 50 , 39 , 58 , 79 , 70 ,
90 , 79 , 97 , 75 . 98 , 77 , 64 , 69 , 82 , 71 ,
65 , 68 , 62 , 73 , 58 , 78 , 75 , 89 , 91 , 99 ,
72 , 62 , 74 , 81 , 79 , 81 , 86 , 78 , 90 , 81
(1)计算这组数据的极差,这个极差说明了什么问题
(2)将数据适当分组,作出频数分布表和频数分布直方图;
(3)这次数学考试的及格率是多少
四、尝试小结
20.2.2 方差
学习目标:
1. 了解方差的定义和计算公式。
2. 理解方差概念的产生和形成的过程。
3. 会用方差计算公式来比较两组数据的波动大小。
重点、难点
1. 重点:方差产生的必要性和应用方差公式解决实际问题。
2. 难点:理解方差公式
学习过程
一、课前准备
1、为什么要学习方差和方差公式?波动性可以通过什么方式表现出来?
方差公式:S= 其中n代表 、代表
2、从甲、乙两种农作物中各抽取1株苗,分别测得它的苗高如下:(单位:cm)
甲:9、10、11、12、7、13、10、8、12、8;
乙:8、13、12、11、10、12、7、7、9、11;
问:(1)哪种农作物的苗长的比较高?
(2)哪种农作物的苗长得比较整齐?
3、 段巍和金志强两人参加体育项目训练,近期的5次测试成绩如下表所示,谁的成绩比较稳定?为什么?
测试次数 1 2 3 4 5
段巍 13 14 13 12 13
金志强 10 13 16 14 12
二、巩固练习
1、已知一组数据为2、0、-1、3、-4,则这组数据的方差为 。
2、甲、乙两名学生在相同的条件下各射靶10次,命中的环数如下:
甲:7、8、6、8、6、5、9、10、7、4
乙:9、5、7、8、7、6、8、6、7、7
经过计算,两人射击环数的平均数相同,但S S,所以确定 去参加比赛。
3、甲、乙两台机床生产同种零件,10天出的次品分别是:
甲:0、1、0、2、2、0、3、1、2、4
乙:2、3、1、2、0、2、1、1、2、1
分别计算出两个样本的平均数和方差,根据你的计算判断哪台机床的性能较好?
4、在一次芭蕾舞的比赛中,甲乙两个芭蕾舞团都表演了舞剧(天鹅湖),参加表演的女演员的身高(单位:cm)分别是
甲团: 163 164 164 165 165 165 166 167
乙团: 163 164 164 165 166 167 167 168
哪个芭蕾舞团的女演员的身高更整齐?
5、小爽和小兵在10次百米跑步练习中成绩如表所示:(单位:秒)
小爽 10.8 10.9 11.0 10.7 11.1 11.1 10.8 11.0 10.7 10.9
小兵 10.9 10.9 10.8 10.8 11.0 10.9 10.8 11.1 10.9 10.8
如果根据这几次成绩选拔一人参加比赛,你会选谁呢?
拓展提高
1、样本为101,98,102,100,99的极差是 , 方差是 .
2、甲、乙两个样本,甲样本方差是2.15,乙样本
方差是2.31,则甲样本和乙样本的离散程度( )
A.甲、乙离散程度一样
B.甲比乙的离散程度大
C.乙比甲的离散程度大
D.无法比较
3、甲、乙两名学生在参加今年体育考试前各做了5次立定跳远测试,两人的平均成绩相同,其中甲所测得成绩的方差是0.005,乙所测得的成绩如下:2.20 m,2.30 m,2.30 m,2.40 m,2.30 m,那么甲、乙的成绩比较( )
A.甲的成绩更稳定 B.乙的成绩更稳定
C.甲、乙的成绩一样稳定 D.不能确定谁的成绩更稳定
4、学校准备进一批新的课桌椅,现有两个厂家的课桌椅质量、价格均相同,按规定,中学生的课桌高度应为70cm,椅子应为40cm左右,学校分别从两个厂家随机选了5套桌椅,测得高度(单位:cm)如下:
甲厂课桌:72 69 70 71 69
甲厂椅子:39 40 40 41 41
乙厂课桌:68 71 72 70 69
乙厂椅子:42 41 39 40 39
你认为学校应该买哪家的课桌椅?
5、某农民几年前承包了甲、乙两片荒山,各栽了100棵蜜橘,成活98%,现已挂果,经济效益显著,为了分析经营情况,他从甲山随意采摘了3棵树上的蜜橘称得质量分别为25,18,20千克;他从乙山随意采摘了4棵树上的蜜橘,称得质量分别为21,24,20千克。
组成一个样本,问:
(1)样本容量是多少?
(2)样本平均数是多少?并估算出甲、乙两山蜜橘的总产量?
(3)甲、乙两山哪个山上蜜橘长势较整齐?
四、尝试小结
165
10
5
身高(cm)
185
175
155
145
15
20
6
10
20
4
人数(人)
60
10
5
噪音/分贝
80
70
50
40
15
20
6
12
18
4
频数
10
90
台数
规格
月份
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
