高二数学新课标人教A版必修二同步课件:2.3.2 平面与平面垂直的判定 课件(共30张PPT)
文档属性
| 名称 | 高二数学新课标人教A版必修二同步课件:2.3.2 平面与平面垂直的判定 课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-14 22:13:15 | ||
图片预览




文档简介
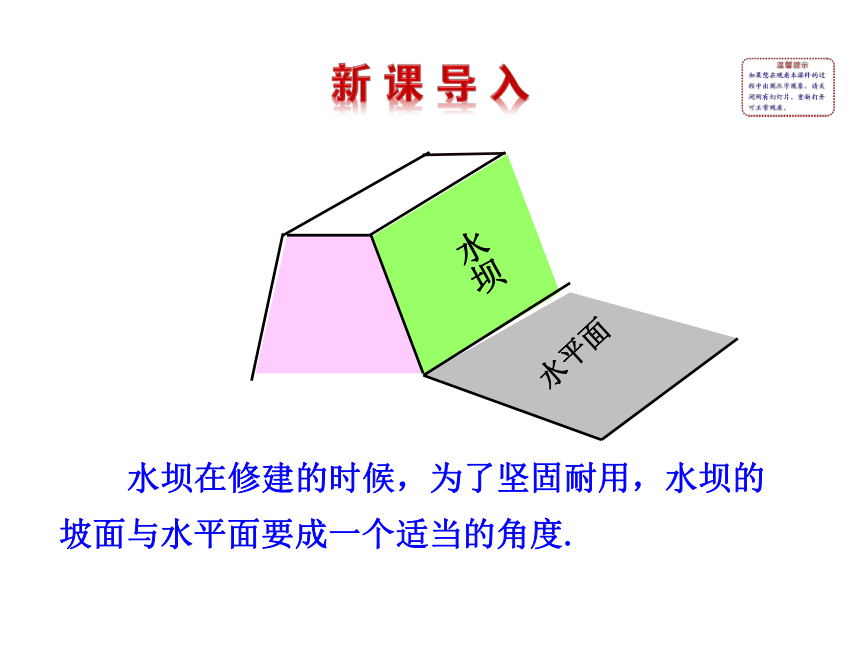
课件30张PPT。2.3.2 平面与平面垂直的判定 建筑施工时,为了保证墙面是竖直的,常使用铅锤来检测,这是什么道理呢?1.理解 “二面角”、“二面角的平面角”及“直
二面角”、“两个平面互相垂直”的概念.
2.掌握两个平面垂直的判定定理并能进行简单应用.
(重点)
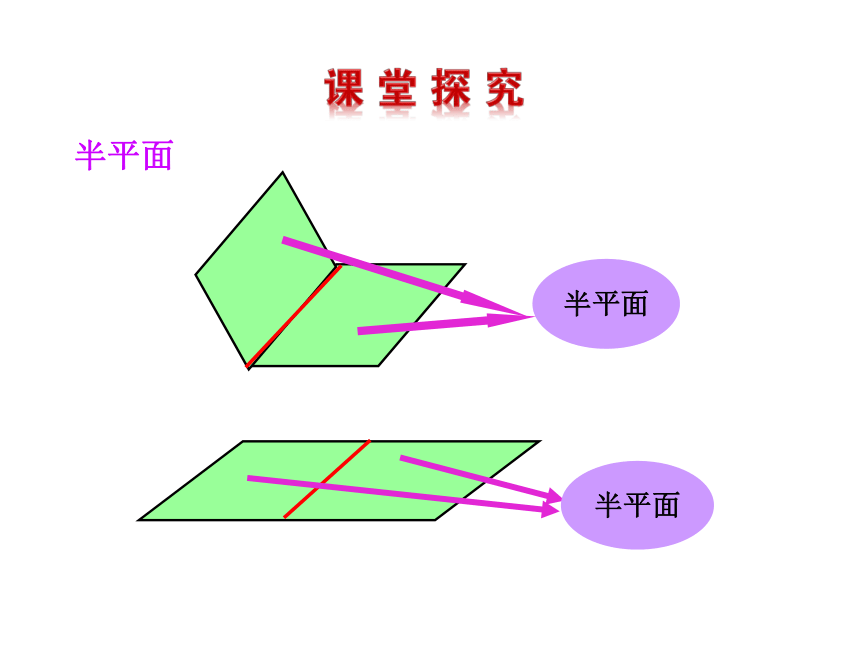
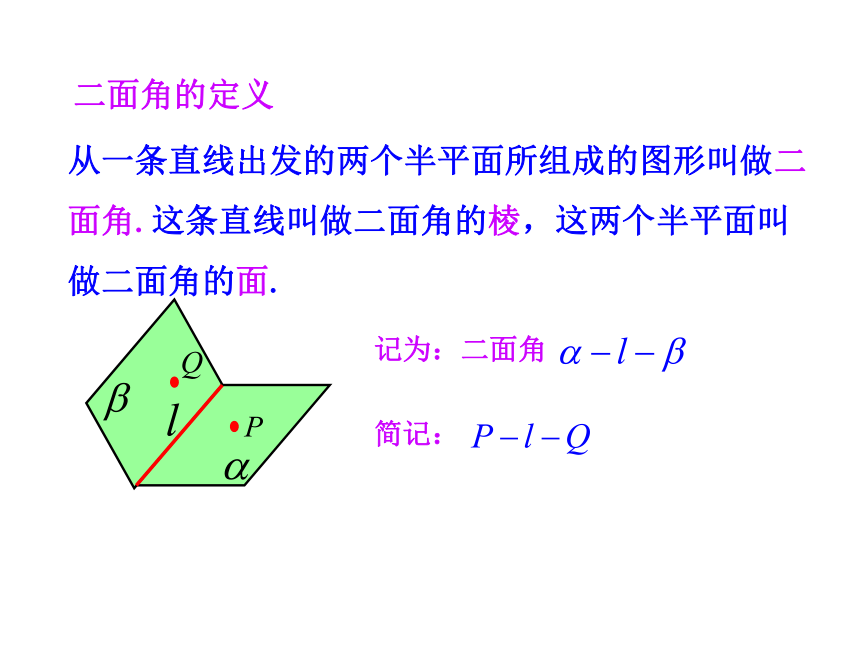
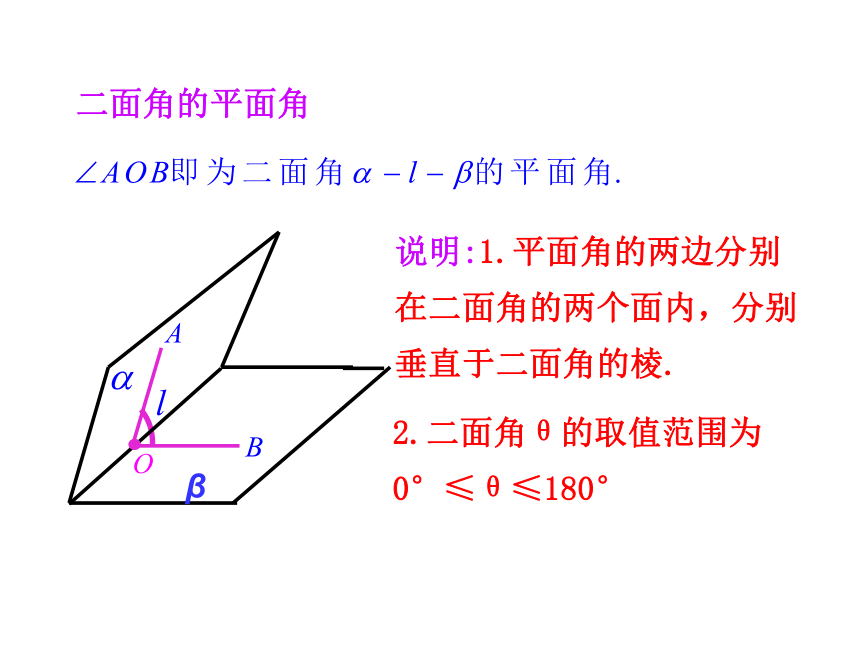
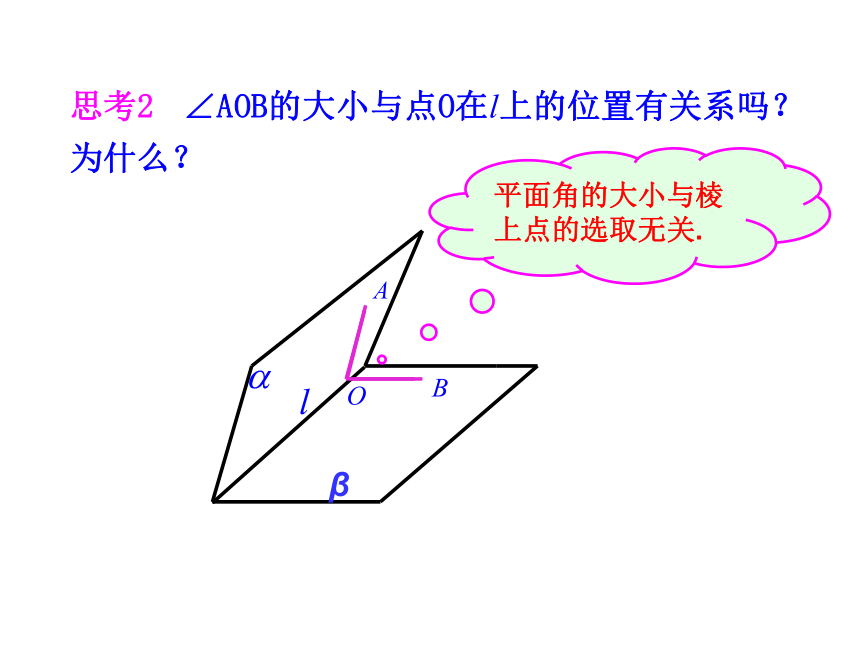
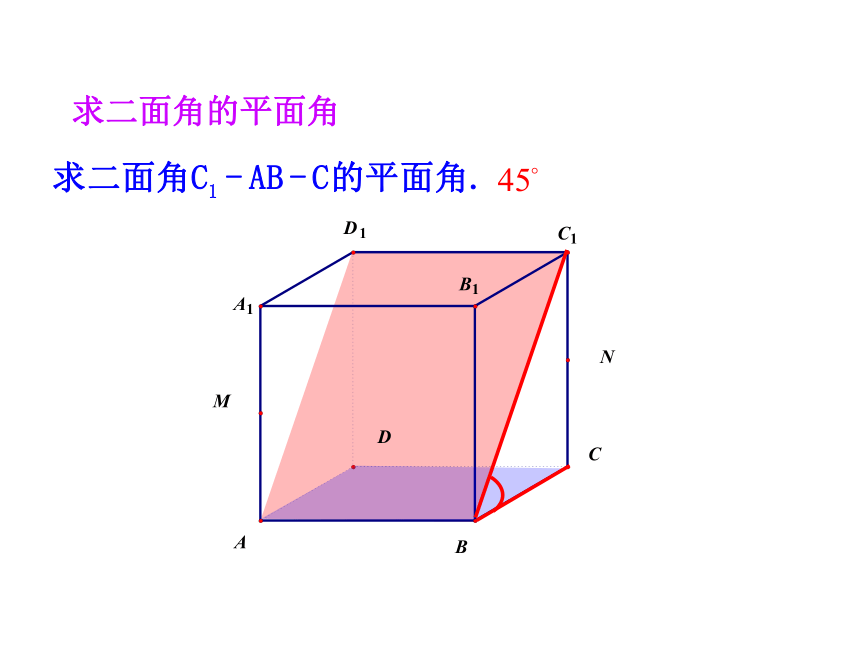
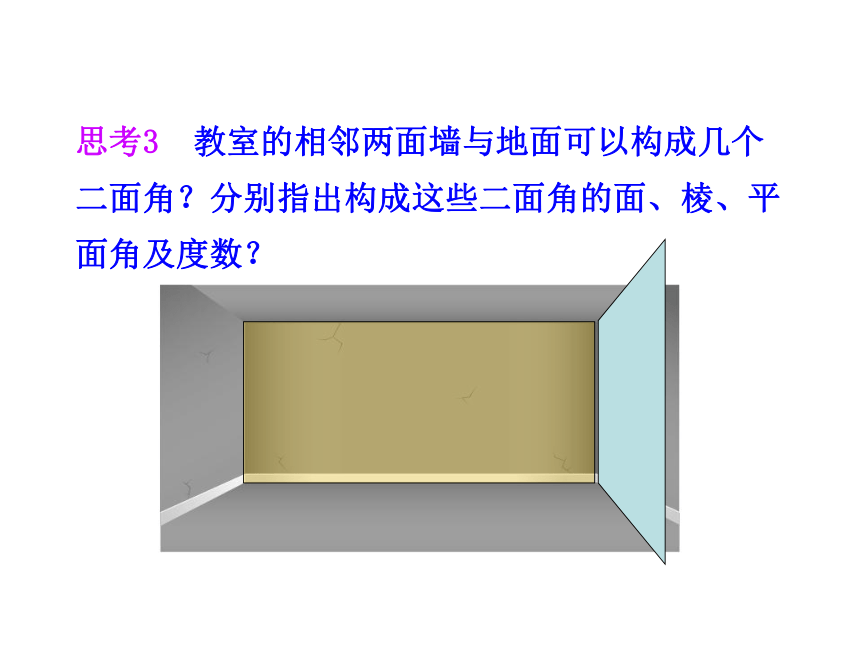
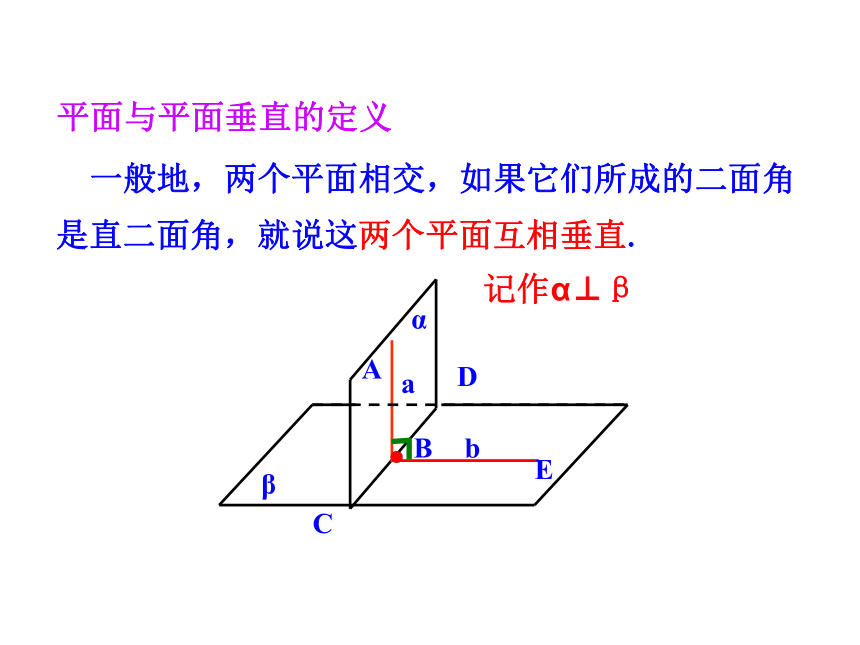
3.培养空间想象能力与转化化归的思想.(难点)半平面从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个半平面叫做二面角的面.记为:二面角简记:二面角的定义思考1 我们常说“把门开大些”,是指哪个角开大一些,我们应该怎么刻画二面角的大小?β2.二面角θ的取值范围为0°≤θ≤180°二面角的平面角说明:1.平面角的两边分别在二面角的两个面内,分别垂直于二面角的棱.β平面角的大小与棱上点的选取无关.求二面角的平面角αP思考3 教室的相邻两面墙与地面可以构成几个二面角?分别指出构成这些二面角的面、棱、平面角及度数?αβ aBbCEAD 一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.记作α⊥β平面与平面垂直的定义注意:把直立平面的竖边画成与水平平面的横边垂直.图形表示思考4 如何检测所砌的墙面和地面是否垂直? 一个平面过另一个平面的垂线,则这两个平面垂直.符号表示:平面与平面垂直的判定定理例1 如图,AB是圆O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,
求证:平面PAC⊥平面PBC.分析:找出在一个面内与另一个面垂直的直线.BC⊥平面PAC证明:设⊙O所在平面为α,由已知条件,有PA⊥α,BC在α内,所以PA⊥BC,
因为点C是圆周上不同于A,B的任意一点,
AB为⊙O的直径,
所以∠BCA=90°, 即BC⊥CA.
又因为 PA与AC是△PAC所在平面内
的两条相交直线,
所以 BC⊥平面PAC,
又因为BC在平面PBC内,
所以平面PAC⊥平面PBC.设两个平面α,β,直线l,下列三个条件:①l⊥α;
②l∥β;③α⊥β.若以其中两个作为前提,另一个
作为结论,则可构成三个命题,这三个命题中正确
命题的个数为 ( )
A.3 B.2 C.1 D.0解:若①,②成立,则l与β内的某一直线a平行,所以a⊥α,所以β⊥α,即③成立;若①③成立,l还可能在β内,所以不能推出l∥β;若②③成立,l也可能平行于α所以不能推出l⊥α,故只有①②?③正确.C【变式练习】2.如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后记为G- SEF,则四面体S-EFG中必有( ).
A.SG⊥△EFG所在平面
B.SD⊥△EFG所在平面
C.GF⊥△SEF所在平面
D.GD⊥△SEF所在平面SG1G2G3EFDSG1G2G3EFDSG⊥△EFG所在平面.故选A.4.如图所示:在Rt△ABC中,∠ABC=90° ,P为△ABC所在平
面外一点,PA⊥平面ABC,你能发现哪些平面互相垂直,
为什么?6. 如图,三棱柱ABC-A1B1C1中,侧棱垂直于底面,∠ACB=90°,AC=BC= AA1,D是棱AA1的中点.
(1)证明:平面BDC1⊥平面BDC.
(2)平面BDC1分此棱柱为两部分,
求这两部分体积的比.找二面角的平面角说明该平面角是直角.(一般通过计算完成证明)(1)定义法:(2)判定定理:要证两个平面垂直,另一个平面的一条垂线.只要在其中一个平面内找到(线面垂直?面面垂直)两个平面垂直的证明方法:面面垂直线面垂直?线线垂直?
二面角”、“两个平面互相垂直”的概念.
2.掌握两个平面垂直的判定定理并能进行简单应用.
(重点)
3.培养空间想象能力与转化化归的思想.(难点)半平面从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个半平面叫做二面角的面.记为:二面角简记:二面角的定义思考1 我们常说“把门开大些”,是指哪个角开大一些,我们应该怎么刻画二面角的大小?β2.二面角θ的取值范围为0°≤θ≤180°二面角的平面角说明:1.平面角的两边分别在二面角的两个面内,分别垂直于二面角的棱.β平面角的大小与棱上点的选取无关.求二面角的平面角αP思考3 教室的相邻两面墙与地面可以构成几个二面角?分别指出构成这些二面角的面、棱、平面角及度数?αβ aBbCEAD 一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.记作α⊥β平面与平面垂直的定义注意:把直立平面的竖边画成与水平平面的横边垂直.图形表示思考4 如何检测所砌的墙面和地面是否垂直? 一个平面过另一个平面的垂线,则这两个平面垂直.符号表示:平面与平面垂直的判定定理例1 如图,AB是圆O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,
求证:平面PAC⊥平面PBC.分析:找出在一个面内与另一个面垂直的直线.BC⊥平面PAC证明:设⊙O所在平面为α,由已知条件,有PA⊥α,BC在α内,所以PA⊥BC,
因为点C是圆周上不同于A,B的任意一点,
AB为⊙O的直径,
所以∠BCA=90°, 即BC⊥CA.
又因为 PA与AC是△PAC所在平面内
的两条相交直线,
所以 BC⊥平面PAC,
又因为BC在平面PBC内,
所以平面PAC⊥平面PBC.设两个平面α,β,直线l,下列三个条件:①l⊥α;
②l∥β;③α⊥β.若以其中两个作为前提,另一个
作为结论,则可构成三个命题,这三个命题中正确
命题的个数为 ( )
A.3 B.2 C.1 D.0解:若①,②成立,则l与β内的某一直线a平行,所以a⊥α,所以β⊥α,即③成立;若①③成立,l还可能在β内,所以不能推出l∥β;若②③成立,l也可能平行于α所以不能推出l⊥α,故只有①②?③正确.C【变式练习】2.如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后记为G- SEF,则四面体S-EFG中必有( ).
A.SG⊥△EFG所在平面
B.SD⊥△EFG所在平面
C.GF⊥△SEF所在平面
D.GD⊥△SEF所在平面SG1G2G3EFDSG1G2G3EFDSG⊥△EFG所在平面.故选A.4.如图所示:在Rt△ABC中,∠ABC=90° ,P为△ABC所在平
面外一点,PA⊥平面ABC,你能发现哪些平面互相垂直,
为什么?6. 如图,三棱柱ABC-A1B1C1中,侧棱垂直于底面,∠ACB=90°,AC=BC= AA1,D是棱AA1的中点.
(1)证明:平面BDC1⊥平面BDC.
(2)平面BDC1分此棱柱为两部分,
求这两部分体积的比.找二面角的平面角说明该平面角是直角.(一般通过计算完成证明)(1)定义法:(2)判定定理:要证两个平面垂直,另一个平面的一条垂线.只要在其中一个平面内找到(线面垂直?面面垂直)两个平面垂直的证明方法:面面垂直线面垂直?线线垂直?
