高二数学新课标人教A版必修二同步课件:2.3.3 直线与平面垂直的性质 课件(共25张PPT)
文档属性
| 名称 | 高二数学新课标人教A版必修二同步课件:2.3.3 直线与平面垂直的性质 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 922.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-14 00:00:00 | ||
图片预览






文档简介
课件25张PPT。2.3.3 直线与平面垂直的性质1.理解直线与平面垂直的性质定理.(重点)
2.能运用性质定理解决一些简单问题.(难点)
3.了解垂直与垂直,垂直与平行间的相互联系. 如图,长方体ABCD—A1B1C1D1中,棱AA1,BB1,CC1,DD1所在直线与底面ABCD的位置关系如何?它们彼此之间具有什么位置关系?垂直 平行课堂探究1 如图,已知直线a,b和平面α,如果 a⊥α,b⊥α,那么,直线a,b一定平行吗?课堂探究2 记直线b和α的交点为O,
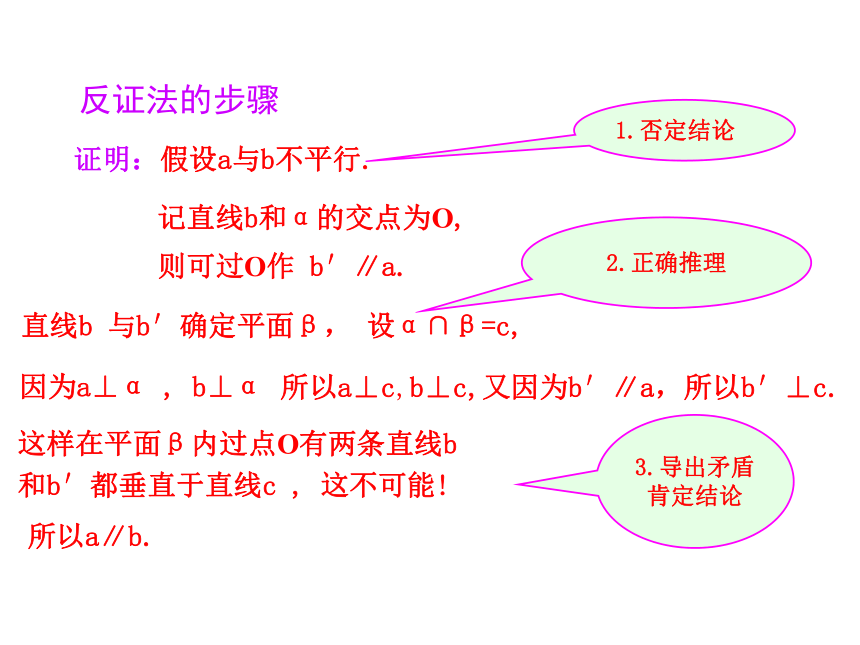
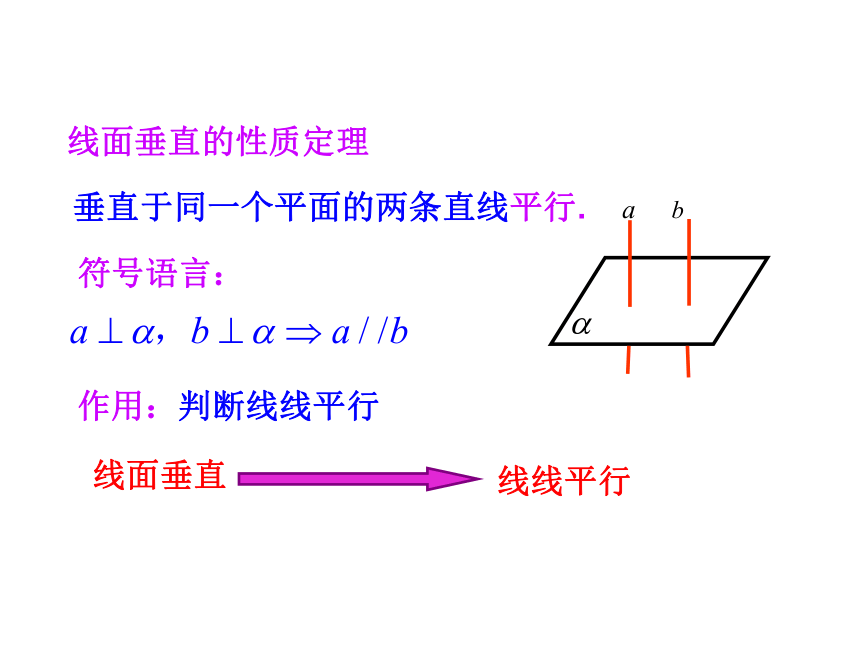
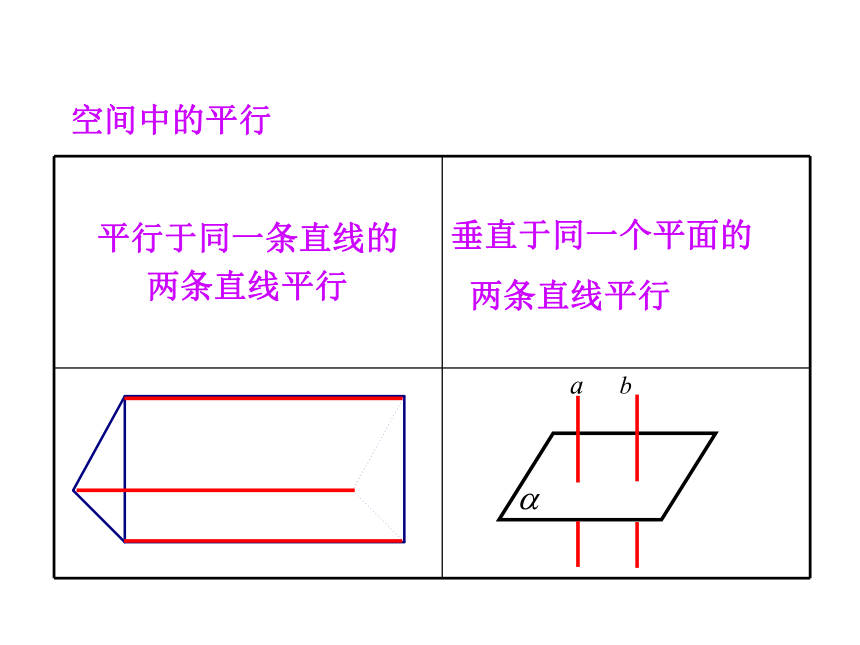
则可过O作 b′∥a.证明:假设a与b不平行.所以a⊥c,b⊥c,又因为b′∥a,所以b′⊥c.这样在平面β内过点O有两条直线b和b′都垂直于直线c , 这不可能!因为a⊥α , b⊥α所以a∥b.直线b 与b′确定平面β, 设α∩β=c,反证法的步骤1.否定结论2.正确推理3.导出矛盾肯定结论垂直于同一个平面的两条直线平行.符号语言:作用:判断线线平行线面垂直的性质定理空间中的平行交换“平行”与“垂直”a⊥α,b⊥αa∥b课堂探究3想一想【解析】取BD中点E,连接AE,CE,
因为几何体为正三棱锥,
所以AE⊥BD,CE⊥BD,
所以BD⊥平面ACE,所以BD⊥AC.
故在平面ABD内,欲过P点作与棱AC垂直的线段,
只需过P作MN∥BD分别交AB,AD于M,N,
则线段MN⊥AC,MN即为所求.设直线a,b分别在正方体中两个不同的平面内,欲使a//b,a,b应满足什么条件?a,b满足下面条件中的任何
一个,都能使a∥b.
(1)a,b同垂直于正方体一个面;
(2)a,b分别在正方体两个相对的
面内且共面;
(3)a,b平行于同一条棱.课堂探究4例 如图,已知α∩β=l,CA⊥α于点A,CB⊥β于
点B,
求证:a∥l.分析:证明:1.给出以下命题,其中错误的是 ( )
A.如果一条直线垂直于一个平面内的无数条直线,则这条直线垂直于这个平面
B.垂直于同一平面的两条直线互相平行
C.垂直于同一直线的两个平面互相平行
D.两条平行直线中的一条垂直于一个平面,则另一条也垂直于这个平面A2.直线l垂直于梯形ABCD的两腰AB和CD,直线m垂直于
AD和BC,则l与m的位置关系是( )
A.相交 B.平行
C.异面 D.不确定3.下面给出三个命题:
①直线l与平面α内两直线都垂直,则l⊥α;
②经过直线a有且仅有一个平面垂直于直线b;
③直线l同时垂直于平面α,β,则α∥β.
其中正确的命题个数为( )
A.3 B.2 C.1 D.0【解析】①中,平面α内两直线不一定相交,所以
①不正确;②中,当a∥b时,不存在平面,所以
②不正确;③是直线与平面垂直的性质,所以③正确.6.(2012·陕西高考)直三棱柱ABC—A1B1C1中,
AB=AA1,∠CAB=
(1)证明:CB1⊥BA1.
(2)已知AB=2,BC= ,求三棱锥C1—ABA1的体积.,2.转化思想:1.直线和平面垂直的性质定理.
证明直线和直线平行的方法.
2.能运用性质定理解决一些简单问题.(难点)
3.了解垂直与垂直,垂直与平行间的相互联系. 如图,长方体ABCD—A1B1C1D1中,棱AA1,BB1,CC1,DD1所在直线与底面ABCD的位置关系如何?它们彼此之间具有什么位置关系?垂直 平行课堂探究1 如图,已知直线a,b和平面α,如果 a⊥α,b⊥α,那么,直线a,b一定平行吗?课堂探究2 记直线b和α的交点为O,
则可过O作 b′∥a.证明:假设a与b不平行.所以a⊥c,b⊥c,又因为b′∥a,所以b′⊥c.这样在平面β内过点O有两条直线b和b′都垂直于直线c , 这不可能!因为a⊥α , b⊥α所以a∥b.直线b 与b′确定平面β, 设α∩β=c,反证法的步骤1.否定结论2.正确推理3.导出矛盾肯定结论垂直于同一个平面的两条直线平行.符号语言:作用:判断线线平行线面垂直的性质定理空间中的平行交换“平行”与“垂直”a⊥α,b⊥αa∥b课堂探究3想一想【解析】取BD中点E,连接AE,CE,
因为几何体为正三棱锥,
所以AE⊥BD,CE⊥BD,
所以BD⊥平面ACE,所以BD⊥AC.
故在平面ABD内,欲过P点作与棱AC垂直的线段,
只需过P作MN∥BD分别交AB,AD于M,N,
则线段MN⊥AC,MN即为所求.设直线a,b分别在正方体中两个不同的平面内,欲使a//b,a,b应满足什么条件?a,b满足下面条件中的任何
一个,都能使a∥b.
(1)a,b同垂直于正方体一个面;
(2)a,b分别在正方体两个相对的
面内且共面;
(3)a,b平行于同一条棱.课堂探究4例 如图,已知α∩β=l,CA⊥α于点A,CB⊥β于
点B,
求证:a∥l.分析:证明:1.给出以下命题,其中错误的是 ( )
A.如果一条直线垂直于一个平面内的无数条直线,则这条直线垂直于这个平面
B.垂直于同一平面的两条直线互相平行
C.垂直于同一直线的两个平面互相平行
D.两条平行直线中的一条垂直于一个平面,则另一条也垂直于这个平面A2.直线l垂直于梯形ABCD的两腰AB和CD,直线m垂直于
AD和BC,则l与m的位置关系是( )
A.相交 B.平行
C.异面 D.不确定3.下面给出三个命题:
①直线l与平面α内两直线都垂直,则l⊥α;
②经过直线a有且仅有一个平面垂直于直线b;
③直线l同时垂直于平面α,β,则α∥β.
其中正确的命题个数为( )
A.3 B.2 C.1 D.0【解析】①中,平面α内两直线不一定相交,所以
①不正确;②中,当a∥b时,不存在平面,所以
②不正确;③是直线与平面垂直的性质,所以③正确.6.(2012·陕西高考)直三棱柱ABC—A1B1C1中,
AB=AA1,∠CAB=
(1)证明:CB1⊥BA1.
(2)已知AB=2,BC= ,求三棱锥C1—ABA1的体积.,2.转化思想:1.直线和平面垂直的性质定理.
证明直线和直线平行的方法.
