高二数学新课标人教A版必修二同步课件:3.1.2 两条直线平行与垂直的判定 课件 (共20张PPT)
文档属性
| 名称 | 高二数学新课标人教A版必修二同步课件:3.1.2 两条直线平行与垂直的判定 课件 (共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 723.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-14 22:17:52 | ||
图片预览





文档简介
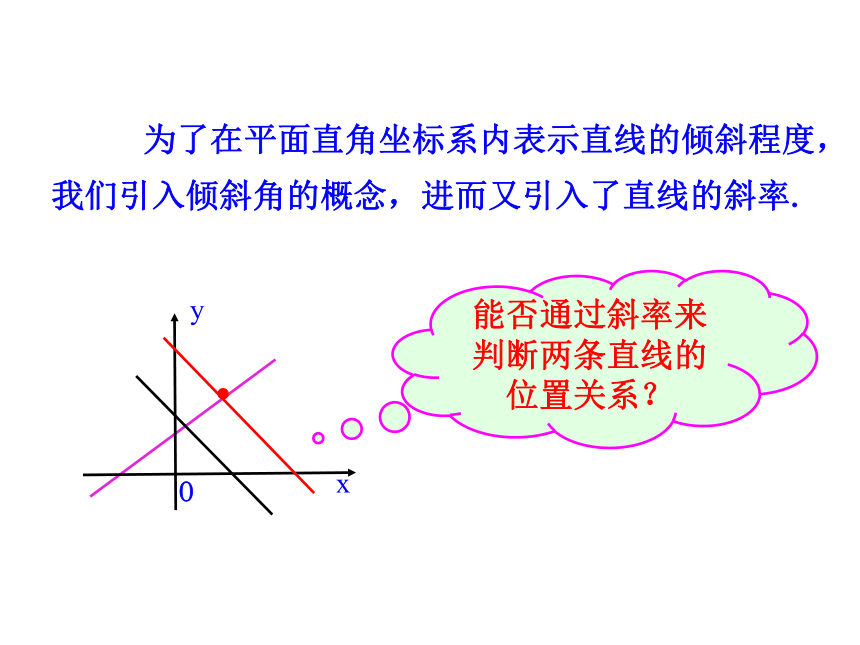
课件20张PPT。3.1.2 两条直线平行与垂直的判定平面内两条直线有哪些位置关系?平行或相交能否通过斜率来判断两条直线的位置关系?xyO. 为了在平面直角坐标系内表示直线的倾斜程度,我们引入倾斜角的概念,进而又引入了直线的斜率.1.理解并掌握两条直线平行与垂直的条件.
(重点)
2.会运用条件判断两直线是否平行或垂直.
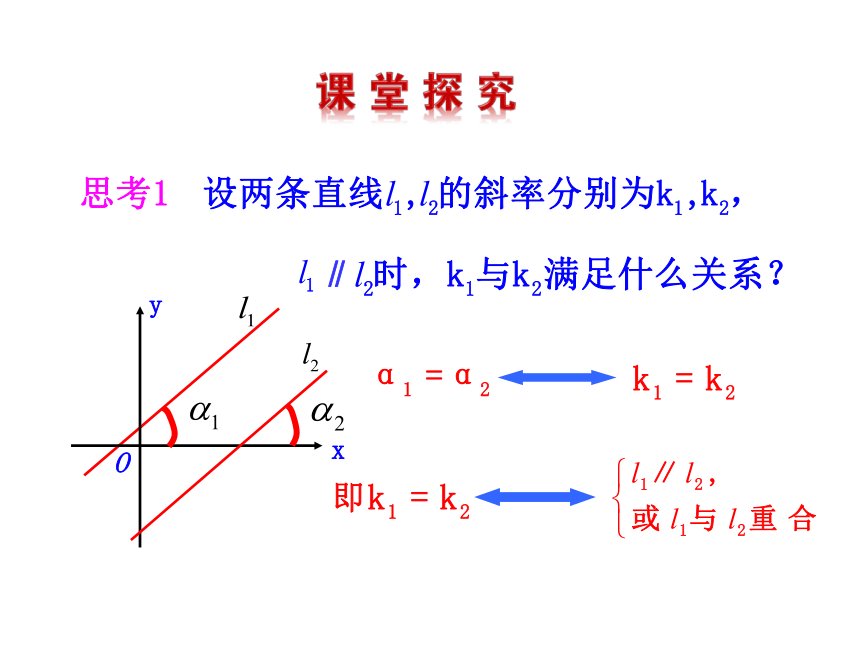
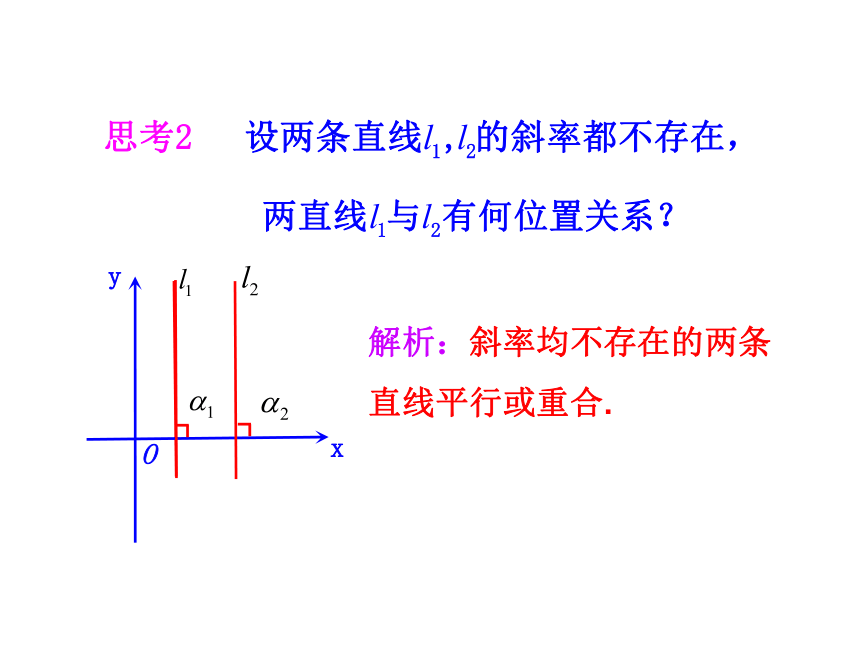
(难点)xyO∥xyO解析:斜率均不存在的两条直线平行或重合.一、两条直线平行的判定特别地,两直线的倾斜角都为90°时,它们互相平行或重合.公式成立的条件:
①两直线不重合;
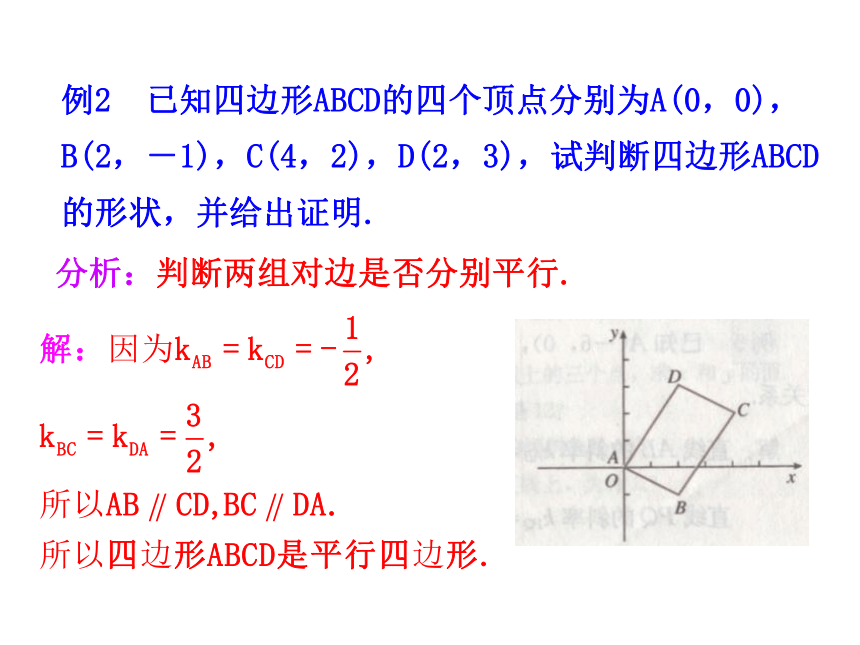
②两直线的斜率均存在.设两条直线 与 的斜率分别为 ,例1 已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论.解:直线BA的斜率直线PQ的斜率例2 已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.分析:判断两组对边是否分别平行.yl1Oxl2反之,成立,可得xyo若一条直线的倾斜角为90°,
另一条直线的倾斜角为0°,
则两直线互相垂直.二、两条直线垂直的判定特别地:一条直线的倾斜角为90°,另一条直线的倾斜角为0°,两直线互相垂直.两直线的斜率均存在.例3 已知A(-6,0),B(3,6),P(0,3),Q(6,-6),试判断直线AB与PQ的位置关系.解:直线AB的斜率直线PQ的斜率分析:分别求出两直线的斜率,观察斜率之间的关系.例4 已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状.分析:结合图形可猜想AB⊥BC,
△ABC为直角三角形.1.已知直线l1过点A(-1,1)和B(-2,-1),直线l2过点
C(1,0)和D(0,a),若l1∥l2,则a的值为( )
A.-2 B.2 C.0 D.
解:选A.l1,l2的斜率分别为2,-a,由l1∥l2,可知
a=-2.2.直线l的倾斜角为30°,若直线l1∥l,则直线l1
的斜率k1=______;若直线l2⊥l,则直线l2的斜率
k2=_______.
解:由斜率定义,直线l的斜率k=tan 30°=
因为l1∥l,所以k1=k= .
因为l2⊥l,所以k2·k=-1,
答案:3.若直线l经过点(a-2,-1)和点(-a-2,1)且与经过点
(-2,1),斜率为 的直线垂直,则实数a的值为____________.4.判断下列各对直线平行还是垂直:
(1)经过两点A(2,3),B(-1,0)的直线l1,与经过点P(1,0)且斜率为-1的直线l2.
(2)经过两点C(3,1),D(-2,0)的直线l3,与经过点 M(1,-4)且斜率为-5的直线l4.解:(1)垂直.解:(2)垂直.5.已知A(1,2),B(-1,0),C(3,4)三点,这三点是否在同一条直线上,为什么?分析:证明两直线斜率相等且有公共点.“几何问题代数化”的思想. 1.两条直线平行的判定:(两条直线不重合且斜率均存在).2.两条直线垂直的判定:(两条直线不重合且斜率均存在)
(重点)
2.会运用条件判断两直线是否平行或垂直.
(难点)xyO∥xyO解析:斜率均不存在的两条直线平行或重合.一、两条直线平行的判定特别地,两直线的倾斜角都为90°时,它们互相平行或重合.公式成立的条件:
①两直线不重合;
②两直线的斜率均存在.设两条直线 与 的斜率分别为 ,例1 已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论.解:直线BA的斜率直线PQ的斜率例2 已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.分析:判断两组对边是否分别平行.yl1Oxl2反之,成立,可得xyo若一条直线的倾斜角为90°,
另一条直线的倾斜角为0°,
则两直线互相垂直.二、两条直线垂直的判定特别地:一条直线的倾斜角为90°,另一条直线的倾斜角为0°,两直线互相垂直.两直线的斜率均存在.例3 已知A(-6,0),B(3,6),P(0,3),Q(6,-6),试判断直线AB与PQ的位置关系.解:直线AB的斜率直线PQ的斜率分析:分别求出两直线的斜率,观察斜率之间的关系.例4 已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状.分析:结合图形可猜想AB⊥BC,
△ABC为直角三角形.1.已知直线l1过点A(-1,1)和B(-2,-1),直线l2过点
C(1,0)和D(0,a),若l1∥l2,则a的值为( )
A.-2 B.2 C.0 D.
解:选A.l1,l2的斜率分别为2,-a,由l1∥l2,可知
a=-2.2.直线l的倾斜角为30°,若直线l1∥l,则直线l1
的斜率k1=______;若直线l2⊥l,则直线l2的斜率
k2=_______.
解:由斜率定义,直线l的斜率k=tan 30°=
因为l1∥l,所以k1=k= .
因为l2⊥l,所以k2·k=-1,
答案:3.若直线l经过点(a-2,-1)和点(-a-2,1)且与经过点
(-2,1),斜率为 的直线垂直,则实数a的值为____________.4.判断下列各对直线平行还是垂直:
(1)经过两点A(2,3),B(-1,0)的直线l1,与经过点P(1,0)且斜率为-1的直线l2.
(2)经过两点C(3,1),D(-2,0)的直线l3,与经过点 M(1,-4)且斜率为-5的直线l4.解:(1)垂直.解:(2)垂直.5.已知A(1,2),B(-1,0),C(3,4)三点,这三点是否在同一条直线上,为什么?分析:证明两直线斜率相等且有公共点.“几何问题代数化”的思想. 1.两条直线平行的判定:(两条直线不重合且斜率均存在).2.两条直线垂直的判定:(两条直线不重合且斜率均存在)
