高二数学新课标人教A版必修五同步课件:2.4 第2课时 等比数列的性质(共26张ppt)(共26张PPT)
文档属性
| 名称 | 高二数学新课标人教A版必修五同步课件:2.4 第2课时 等比数列的性质(共26张ppt)(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 592.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-15 18:41:53 | ||
图片预览







文档简介
课件26张PPT。第2课时 等比数列的性质 定义:一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0).复习回顾如果一个数列是等比数列,它的公比是q,那么由此可知,等比数列 的通项公式为…1.理解并掌握等比数列的性质及其初步应用.
(重点、难点)
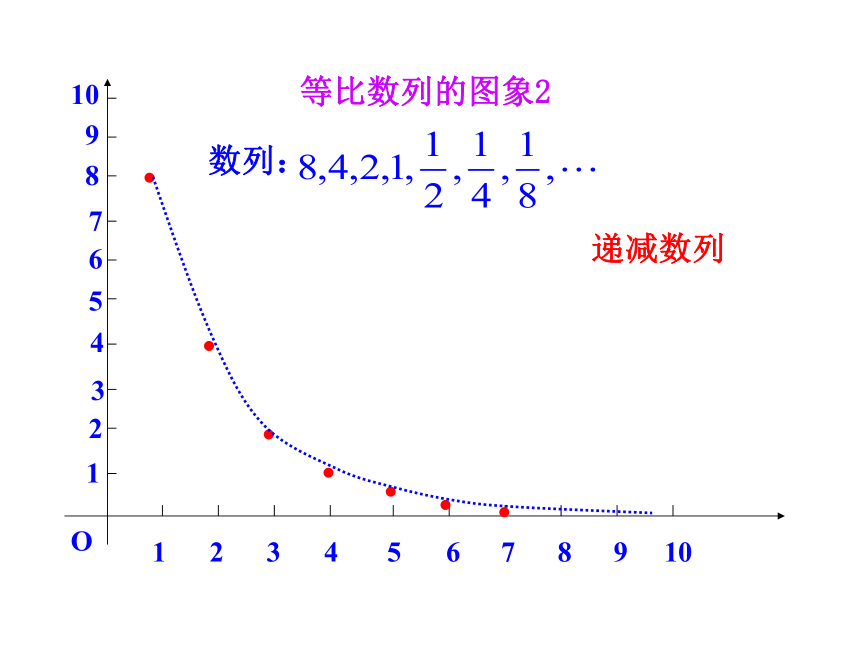
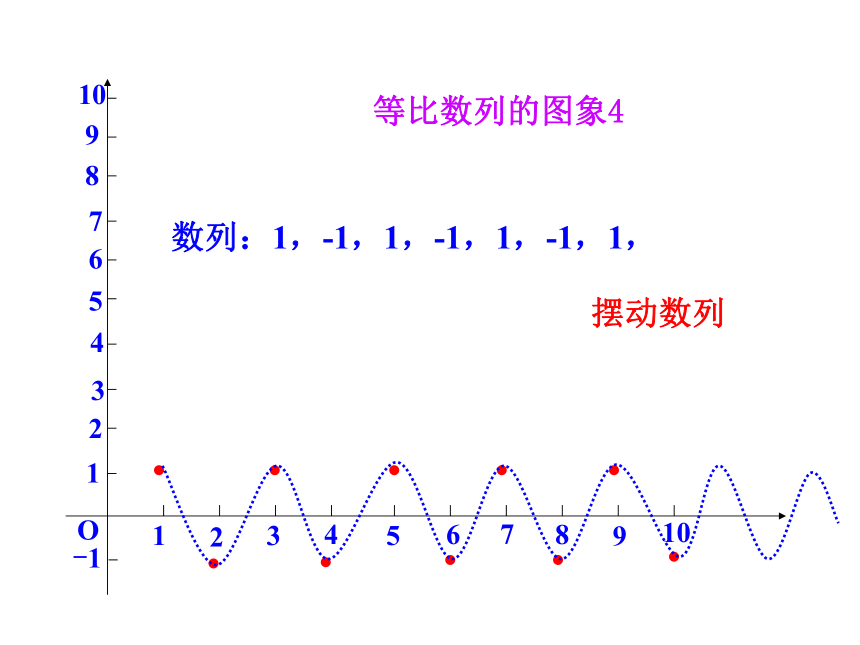
2.引导学生学习观察、类比、猜测等推理方法,提高学生分析、综合、抽象、概括等逻辑思维能力.(1) 1,2,4,8,16,…观察数列(3) 4,4,4,4,4,4,4,…(4) 1,-1,1,-1,1,-1,1,…公比 q=2公比 q=公比 q=1公比 q=-1探究点1:等比数列的图象等比数列的图象1数列:1,2,4,8,16,…123456789102468101214161820O●●●●●递增数列通过图象观察性质等比数列的图象212345678910O数列:●●●●●●●12345678910递减数列等比数列的图象3123456789102468101214161820O数列:4,4,4,4,4,4,4,…●●●●●●●●●●常数列等比数列的图象412345678910O12345678910●●●●●●●●●●数列:1,-1,1,-1,1,-1,1,摆动数列-1 类比等差数列的性质,等比数列有哪些性质呢?探究点2:等差、等比数列的性质比较an-an-1=d (n≥2)
常数减—除加—乘加-乘乘—乘方 迭加法迭乘法等比数列用“比”代替了等差数列中的“差”定义数学表
达式通项公式证明通项 公式由等差数列的性质,猜想等比数列的性质猜想1: 若bn-k,bn,bn+k
是{bn}中的三项,则若n+m=p+q,则
bn·bm=bp·bq猜想3: 若{dn}是公比为q′的等比数列,则数列{bn?dn}是公比为q·q′的等比数列.猜想4:从原数列中取出偶数项,组成的新数列公比为 (可推广) 猜想5:若数列{an}是公比为q的等比数列,则当q>1,a1>0或0 当q>1, a1<0或00时, {an}是递减数列;
当q=1时, {an}是常数列;
当q<0时, {an}是摆动数列.(2)an≠0,且anan+2>0.(3)an=amqn-m(n,m∈N*).(4)当n+m=p+q(n,m,p,q∈N*)时,有anam=apaq.(5)当{an}是有穷数列时,与首末两项等距离的两项的积都相等,且等于首末两项的积.【知识提升】(7)若{bn}是公比为q′的等比数列,则数列{an? bn }是公比为qq′的等比数列.(6)数列{λan}(λ为不等于零的常数)仍是公比为q的等比数列.(9)在{an}中,每隔k(k∈N*)项取出一项,按原来顺序排
列,所得的新数列仍为等比数列,且公比为qk+1.(10)当m,n,p(m,n,p∈N*)成等差数列时,am , an , ap 成等比数列.例 已知{an}、{bn}是项数相同的等比数列,求证{an?bn}是等比数列.证明:设数列{an}的首项是a1,公比为q1; {bn}的首项为b1,公比为q2,那么数列{an?bn}的第n项与第n+1项分别为:它是一个与n无关的常数,所以{an?bn}是一个以q1q2为公比的等比数列.A.7 B.5 C.-5 D.-71.已知为等比数列,,,解析:选D. ,D( )则2. 在等差数列{an}中,a3+a11=8,数列{bn}是等比数列,且b7=a7,则b6·b8的值为 ( )
A.2 B.4 C.8 D.16D解析:选D.因为{an}为等差数列,所以 =4=b7.又{bn}为等比数列,所以b6·b8 = =16.3.(2013·福建高考)已知等比数列 的公比为q,记 ,
cn=am(n-1)+1·am(n-1)+2·…·am(n-1)+m ,则以下结
论一定正确的是( )
A. 数列 为等差数列,公差为
B. 数列 为等比数列,公比为q2m
C. 数列 为等比数列,公比为
D. 数列 为等比数列,公比为 C【解题指南】如何判定一个数列是等差或等比数列,
注意一定是作差,或作比,看看是不是常数.解析:选C.显然, 不可能是等比数列; 是等比数列;证明如下:4.在等比数列{an}中,an>0,a2 a4+2a3a5+a4a6=36,
那么a3+a5= _ .
5.在等比数列{an}中, a15 =10, a45=90,则
a30 =__________.
6.在等比数列{an}中,a1+a2 =30, a3+a4 =120,
则a5+a6=_____.630480或-30则对所有的自然数 n 都成立,则公比 q =___________.1.证明或判断一个数列为等比数列的方法:
(1) =q (n?2 且q≠0)?{an}为等比数列.
(适用于选择题、填空题和解答题)
(2)an=cqn (c,q≠0)?{an}为等比数列.
(适用于选择题、填空题)
(3)a2n+1=anan+2?{an}为等比数列.
(适用于选择题、填空题)2.等比数列的性质:
(1)an=amqn-m(n,m∈N*)
(2)若m+n=p+q,则aman= apaq(m,n,p,q∈N*)
(3)等比数列中,每隔k项取一项,按原来顺序排列,所得的新数列仍为等比数列.
(4)a1a2, a3a4, a5a6, …仍为等比数列.
(5)在等比数列中,从第二项起,每一项都是它等距离的前后两项的等比中项.
(重点、难点)
2.引导学生学习观察、类比、猜测等推理方法,提高学生分析、综合、抽象、概括等逻辑思维能力.(1) 1,2,4,8,16,…观察数列(3) 4,4,4,4,4,4,4,…(4) 1,-1,1,-1,1,-1,1,…公比 q=2公比 q=公比 q=1公比 q=-1探究点1:等比数列的图象等比数列的图象1数列:1,2,4,8,16,…123456789102468101214161820O●●●●●递增数列通过图象观察性质等比数列的图象212345678910O数列:●●●●●●●12345678910递减数列等比数列的图象3123456789102468101214161820O数列:4,4,4,4,4,4,4,…●●●●●●●●●●常数列等比数列的图象412345678910O12345678910●●●●●●●●●●数列:1,-1,1,-1,1,-1,1,摆动数列-1 类比等差数列的性质,等比数列有哪些性质呢?探究点2:等差、等比数列的性质比较an-an-1=d (n≥2)
常数减—除加—乘加-乘乘—乘方 迭加法迭乘法等比数列用“比”代替了等差数列中的“差”定义数学表
达式通项公式证明通项 公式由等差数列的性质,猜想等比数列的性质猜想1: 若bn-k,bn,bn+k
是{bn}中的三项,则若n+m=p+q,则
bn·bm=bp·bq猜想3: 若{dn}是公比为q′的等比数列,则数列{bn?dn}是公比为q·q′的等比数列.猜想4:从原数列中取出偶数项,组成的新数列公比为 (可推广) 猜想5:若数列{an}是公比为q的等比数列,则当q>1,a1>0或0
当q=1时, {an}是常数列;
当q<0时, {an}是摆动数列.(2)an≠0,且anan+2>0.(3)an=amqn-m(n,m∈N*).(4)当n+m=p+q(n,m,p,q∈N*)时,有anam=apaq.(5)当{an}是有穷数列时,与首末两项等距离的两项的积都相等,且等于首末两项的积.【知识提升】(7)若{bn}是公比为q′的等比数列,则数列{an? bn }是公比为qq′的等比数列.(6)数列{λan}(λ为不等于零的常数)仍是公比为q的等比数列.(9)在{an}中,每隔k(k∈N*)项取出一项,按原来顺序排
列,所得的新数列仍为等比数列,且公比为qk+1.(10)当m,n,p(m,n,p∈N*)成等差数列时,am , an , ap 成等比数列.例 已知{an}、{bn}是项数相同的等比数列,求证{an?bn}是等比数列.证明:设数列{an}的首项是a1,公比为q1; {bn}的首项为b1,公比为q2,那么数列{an?bn}的第n项与第n+1项分别为:它是一个与n无关的常数,所以{an?bn}是一个以q1q2为公比的等比数列.A.7 B.5 C.-5 D.-71.已知为等比数列,,,解析:选D. ,D( )则2. 在等差数列{an}中,a3+a11=8,数列{bn}是等比数列,且b7=a7,则b6·b8的值为 ( )
A.2 B.4 C.8 D.16D解析:选D.因为{an}为等差数列,所以 =4=b7.又{bn}为等比数列,所以b6·b8 = =16.3.(2013·福建高考)已知等比数列 的公比为q,记 ,
cn=am(n-1)+1·am(n-1)+2·…·am(n-1)+m ,则以下结
论一定正确的是( )
A. 数列 为等差数列,公差为
B. 数列 为等比数列,公比为q2m
C. 数列 为等比数列,公比为
D. 数列 为等比数列,公比为 C【解题指南】如何判定一个数列是等差或等比数列,
注意一定是作差,或作比,看看是不是常数.解析:选C.显然, 不可能是等比数列; 是等比数列;证明如下:4.在等比数列{an}中,an>0,a2 a4+2a3a5+a4a6=36,
那么a3+a5= _ .
5.在等比数列{an}中, a15 =10, a45=90,则
a30 =__________.
6.在等比数列{an}中,a1+a2 =30, a3+a4 =120,
则a5+a6=_____.630480或-30则对所有的自然数 n 都成立,则公比 q =___________.1.证明或判断一个数列为等比数列的方法:
(1) =q (n?2 且q≠0)?{an}为等比数列.
(适用于选择题、填空题和解答题)
(2)an=cqn (c,q≠0)?{an}为等比数列.
(适用于选择题、填空题)
(3)a2n+1=anan+2?{an}为等比数列.
(适用于选择题、填空题)2.等比数列的性质:
(1)an=amqn-m(n,m∈N*)
(2)若m+n=p+q,则aman= apaq(m,n,p,q∈N*)
(3)等比数列中,每隔k项取一项,按原来顺序排列,所得的新数列仍为等比数列.
(4)a1a2, a3a4, a5a6, …仍为等比数列.
(5)在等比数列中,从第二项起,每一项都是它等距离的前后两项的等比中项.
