二次函数重难点专题训练卷(2)
图片预览


文档简介
二次函数重难点专题训练卷(2)
班级 姓名
选择题
1、二次函数y=ax2+bx+c(a,b,c为常数且a≠0)的图象如图所示,则一次函数y=ax+b与反比例函数y=的图象可能是( )【出处:21教育名师】
A. B. C. D.
2、如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )21教育名师原创作品
A.一直减小 B.一直不变 C.先减小后增大 D.先增大后减小
3、已知二次函数y=x2+bx+c与x轴只有一个交点,且图象过A(x1,m)、B(x1+n,m)两点,则m、n的关系为( )
A.m=n B.m=n C.m=n2 D.m=n2
4、如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )
A.2a﹣b=0
B.a+b+c>0
C.3a﹣c=0
D.当a=时,△ABD是等腰直角三角形
5、已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )
A. B. C. D.2
6、已知a≥2,m2﹣2am+2=0,n2﹣2an+2=0,则(m﹣1)2+(n﹣1)2的最小值是( )
A.6 B.3 C.﹣3 D.0
7、若二次函数y=ax2﹣2ax+c的图象经过点(﹣1,0),则方程ax2﹣2ax+c=0的解为( )
A.x1=﹣3,x2=﹣1 B.x1=1,x2=3 C.x1=﹣1,x2=3 D.x1=﹣3,x2=1
8、在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
A.y1<y2 B.y1>y2 C.y的最小值是﹣3 D.y的最小值是﹣4
二、填空题
9、设x1、x2是方程5x2﹣3x﹣2=0的两个实数根,则+的值为 .
10、已知抛物线y=ax2+bx+c开口向上且经过点(1,1),双曲线y=经过点(a,bc),给出下列结论:①bc>0;②b+c>0;③b,c是关于x的一元二次方程x2+(a﹣1)x+=0的两个实数根;④a﹣b﹣c≥3.其中正确结论是 (填写序号)
解答题
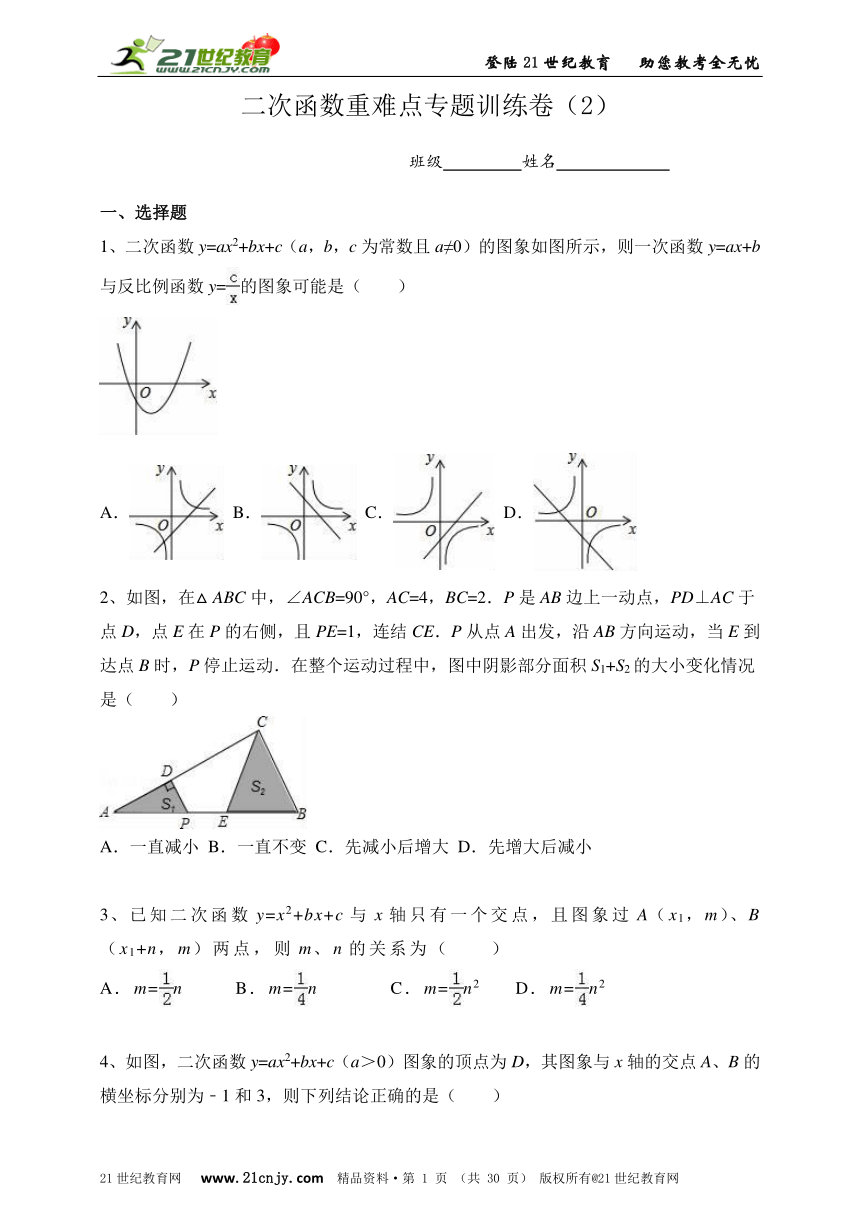
11、二次函数的图象经过点(4,3),(3,0)。
(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴;
(3)在所给坐标系中画出二次函数的图象。
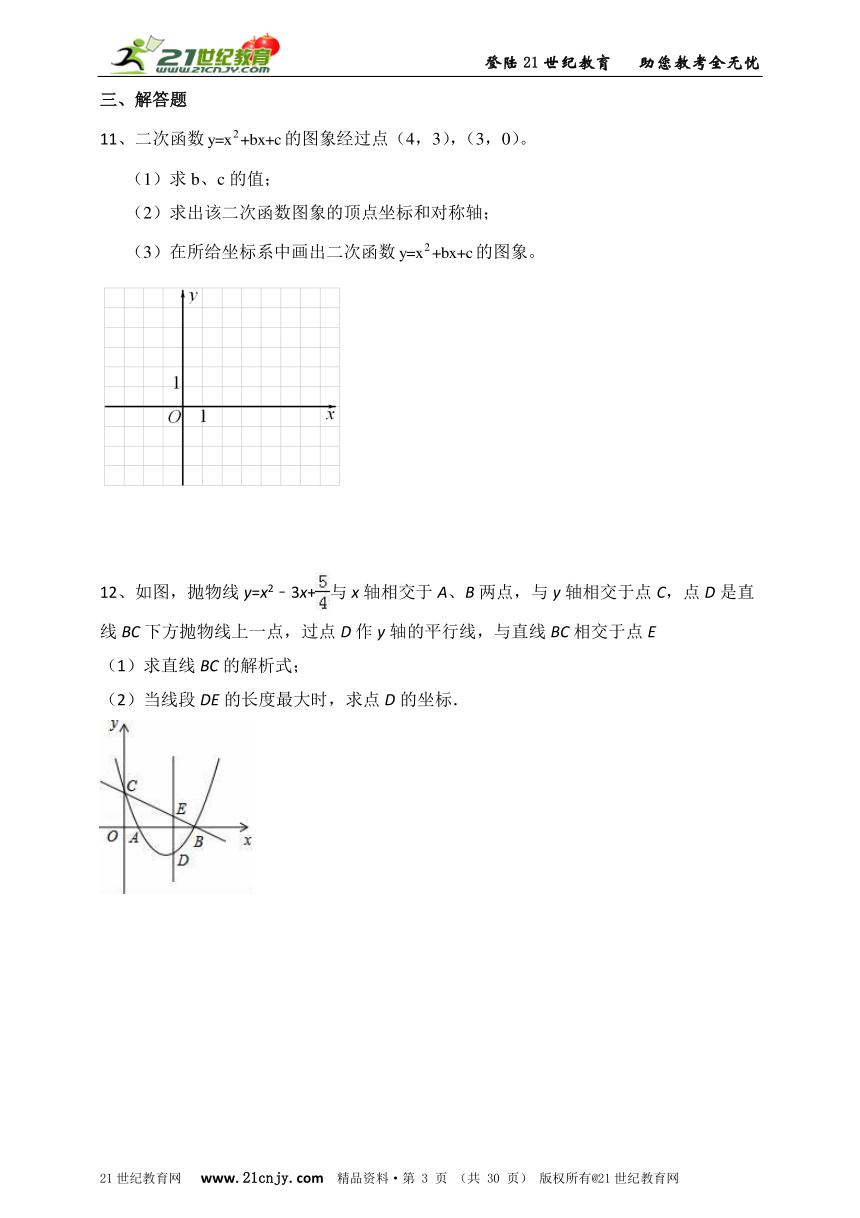
12、如图,抛物线y=x2﹣3x+与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标.
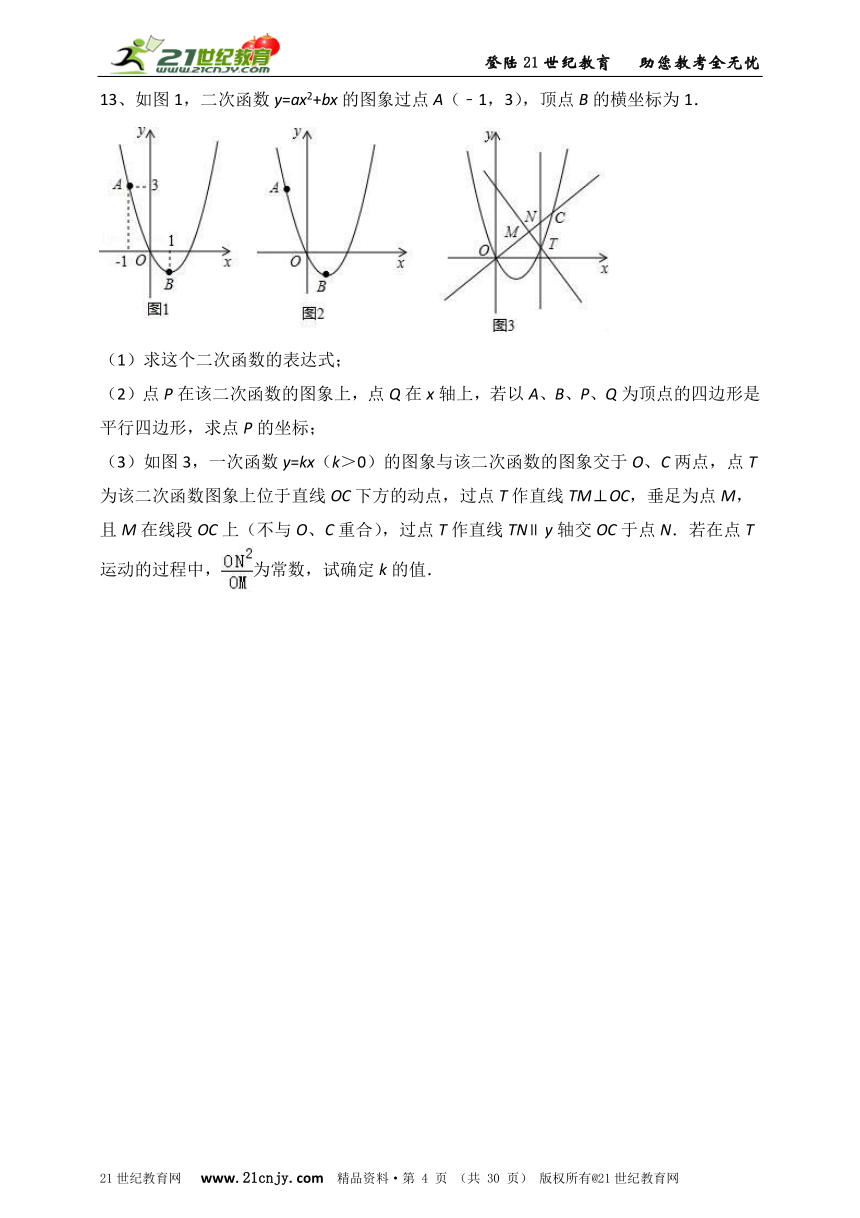
13、如图1,二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1.
(1)求这个二次函数的表达式;
(2)点P在该二次函数的图象上,点Q在x轴上,若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;
(3)如图3,一次函数y=kx(k>0)的图象与该二次函数的图象交于O、C两点,点T为该二次函数图象上位于直线OC下方的动点,过点T作直线TM⊥OC,垂足为点M,且M在线段OC上(不与O、C重合),过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中,为常数,试确定k的值.
14、如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(1)用含m的代数式表示BE的长.
(2)当m=时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
15、抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,-3)、B(4,0),
① 求该抛物线的解析式;
② 若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2) 如图2,已知直线PA、PB与y轴分别交于E、F两点.当点P运动时,是否为定值?若是,试求出该定值;若不是,请说明理由.21世纪教育网版权所有
16、如图,在平面直角坐标系xOy中,将二次函数y=x2﹣1的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N. 21cnjy.com
(1)求N的函数表达式;
(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求PA2+PB2的最大值;
(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数. 21·世纪*教育网
17、已知抛物线与x轴交于A(6,0)、B(﹣,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.【版权所有:21教育】
(1)求此抛物线的解析式;
(2)如图1,将△OMN沿x轴向右平移t个单位(0≤t≤5)到△O′M′N′的位置,MN′、M′O′与直线AC分别交于点E、F.21*cnjy*com
①当点F为M′O′的中点时,求t的值;
②如图2,若直线M′N′与抛物线相交于点G,过点G作GH∥M′O′交AC于点H,试确定线段EH是否存在最大值?若存在,求出它的最大值及此时t的值;若不存在,请说明理由.
18、如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)2-1-c-n-j-y
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
二次函数重难点专题训练卷(2)
答案详解
一、选择题
2、如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )www.21-cn-jy.com
A.一直减小 B.一直不变 C.先减小后增大 D.先增大后减小
【解答】解:在RT△ABC中,∵∠ACB=90°,AC=4,BC=2,
∴AB===2,设PD=x,AB边上的高为h,
h==,
∵PD∥BC,
∴=,
∴AD=2x,AP=x,
∴S1+S2=?2x?x+(2﹣1﹣x)?=x2﹣2x+4﹣=(x﹣1)2+3﹣,
∴当0<x<1时,S1+S2的值随x的增大而减小,
当1≤x≤2时,S1+S2的值随x的增大而增大.
故选C.
3、已知二次函数y=x2+bx+c与x轴只有一个交点,且图象过A(x1,m)、B(x1+n,m)两点,则m、n的关系为( )2·1·c·n·j·y
A.m=n B.m=n C.m=n2 D.m=n2
【解答】解:∵抛物线y=x2+bx+c与x轴只有一个交点,
∴当x=﹣时,y=0.且b2﹣4c=0,即b2=4c.
又∵点A(x1,m),B(x1+n,m),
∴点A、B关于直线x=﹣对称,
∴A(﹣﹣,m),B(﹣+,m),
将A点坐标代入抛物线解析式,得m=(﹣﹣)2+(﹣﹣)b+c,即m=﹣+c,
∵b2=4c,
∴m=n2,
故选D.
4、如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )【来源:21cnj*y.co*m】
A.2a﹣b=0
B.a+b+c>0
C.3a﹣c=0
D.当a=时,△ABD是等腰直角三角形
【解答】解:∵抛物线与x轴的交点A、B的横坐标分别为﹣1,3,
∴抛物线的对称轴为直线x=1,则﹣=1,
∴2a+b=0,
∴选项A错误;
∴当自变量取1时,对应的函数图象在x轴下方,
∴x=1时,y<0,则a+b+c<0,
∴选项B错误;
∵A点坐标为(﹣1,0),
∴a﹣b+c=0,而b=﹣2a,
∴a+2a+c=0,
∴3a+c=0,
∴选项C错误;
当a=,则b=﹣1,c=﹣,对称轴x=1与x轴的交点为E,如图,
∴抛物线的解析式为y=x2﹣x﹣,
把x=1代入得y=﹣1﹣=﹣2,
∴D点坐标为(1,﹣2),
∴AE=2,BE=2,DE=2,
∴△ADE和△BDE都为等腰直角三角形,
∴△ADB为等腰直角三角形,
∴选项D正确.
故选D.
5、已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )
A. B. C. D.2
【解答】解:令y=0,则﹣x2﹣2x+3=0,解得x=﹣3或1,不妨设A(﹣3,0),B(1,0),
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点C(﹣1,4),
如图所示,作CD⊥AB于D.
在RT△ACD中,tan∠CAD===2,
故答案为D.
6、已知a≥2,m2﹣2am+2=0,n2﹣2an+2=0,则(m﹣1)2+(n﹣1)2的最小值是( )
A.6 B.3 C.﹣3 D.0
【解答】解:∵m2﹣2am+2=0,n2﹣2an+2=0,
∴m,n是关于x的方程x2﹣2ax+2=0的两个根,
∴m+n=2a,mn=2,
∴(m﹣1)2+(n﹣1)2=m2﹣2m+1+n2﹣2n+1=(m+n)2﹣2mn﹣2(m+n)+2=4a2﹣4﹣4a+2=4(a﹣)2﹣3,
∵a≥2,
∴当a=2时,(m﹣1)2+(n﹣1)2有最小值,
∴(m﹣1)2+(n﹣1)2的最小值=4(a﹣)2+3=4(2﹣)2﹣3=6,
故选A.
7、若二次函数y=ax2﹣2ax+c的图象经过点(﹣1,0),则方程ax2﹣2ax+c=0的解为( )
A.x1=﹣3,x2=﹣1 B.x1=1,x2=3 C.x1=﹣1,x2=3 D.x1=﹣3,x2=1
【解答】解:∵二次函数y=ax2﹣2ax+c的图象经过点(﹣1,0),
∴方程ax2﹣2ax+c=0一定有一个解为:x=﹣1,
∵抛物线的对称轴为:直线x=1,
∴二次函数y=ax2﹣2ax+c的图象与x轴的另一个交点为:(3,0),
∴方程ax2﹣2ax+c=0的解为:x1=﹣1,x2=3.
故选:C.
8、在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
A.y1<y2 B.y1>y2 C.y的最小值是﹣3 D.y的最小值是﹣4
【解答】解:y=x2+2x﹣3=(x+3)(x﹣1),
则该抛物线与x轴的两交点横坐标分别是﹣3、1.
又y=x2+2x﹣3=(x+1)2﹣4,
∴该抛物线的顶点坐标是(﹣1,﹣4),对称轴为x=﹣1.
A、无法确定点A、B离对称轴x=﹣1的远近,故无法判断y1与y2的大小,故本选项错误;
B、无法确定点A、B离对称轴x=﹣1的远近,故无法判断y1与y2的大小,故本选项错误;
C、y的最小值是﹣4,故本选项错误;
D、y的最小值是﹣4,故本选项正确.
故选:D.
二、填空题
9、设x1、x2是方程5x2﹣3x﹣2=0的两个实数根,则+的值为 ﹣ .
【解答】解:∵方程x1、x2是方程5x2﹣3x﹣2=0的两个实数根,
∴x1+x2=,x1x2=﹣,
∴+===﹣.
故答案为:﹣.
10、已知抛物线y=ax2+bx+c开口向上且经过点(1,1),双曲线y=经过点(a,bc),给出下列结论:①bc>0;②b+c>0;③b,c是关于x的一元二次方程x2+(a﹣1)x+=0的两个实数根;④a﹣b﹣c≥3.其中正确结论是 ①③ (填写序号)
【解答】解:∵抛物线y=ax2+bx+c开口向上且经过点(1,1),双曲线y=经过点(a,bc), 21*cnjy*com
∴
∴bc>0,故①正确;
∴a>1时,则b、c均小于0,此时b+c<0,
当a=1时,b+c=0,则与题意矛盾,
当0<a<1时,则b、c均大于0,此时b+c>0,
故②错误;
∴x2+(a﹣1)x+=0可以转化为:x2+(b+c)x+bc=0,得x=b或x=c,故③正确;
∵b,c是关于x的一元二次方程x2+(a﹣1)x+=0的两个实数根,
∴a﹣b﹣c=a﹣(b+c)=a+(a﹣1)=2a﹣1,
当a>1时,2a﹣1>3,
当0<a<1时,﹣1<2a﹣1<3,
故④错误;
故答案为:①③.
解答题
11、二次函数的图象经过点(4,3),(3,0)。
(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴;
(3)在所给坐标系中画出二次函数的图象。
【解答】 解:(1)∵二次函数的图象经过点(4,3),(3,0),
∴,解得。
(2)∵该二次函数为。
∴该二次函数图象的顶点坐标为(2,-1),对称轴为x=1。
(3)列表如下:
x
···
0
1
2
3
4
···
y
···
3
0
1
0
3
···
描点作图如下:
12、如图,抛物线y=x2﹣3x+与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标.
【解答】解:(1)∵抛物线y=x2﹣3x+与x轴相交于A、B两点,与y轴相交于点C,
∴令y=0,可得x=或x=,
∴A(,0),B(,0);
令x=0,则y=,
∴C点坐标为(0,),
设直线BC的解析式为:y=kx+b,则有,
,
解得:,
∴直线BC的解析式为:y=x;
(2)设点D的横坐标为m,则纵坐标为(m,),
∴E点的坐标为(m, m),
设DE的长度为d,
∵点D是直线BC下方抛物线上一点,
则d=m+﹣(m2﹣3m+),
整理得,d=﹣m2+m,
∵a=﹣1<0,
∴当m==时,d最大===,
∴D点的坐标为(,).
13、如图1,二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1.
(1)求这个二次函数的表达式;
(2)点P在该二次函数的图象上,点Q在x轴上,若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;21·cn·jy·com
(3)如图3,一次函数y=kx(k>0)的图象与该二次函数的图象交于O、C两点,点T为该二次函数图象上位于直线OC下方的动点,过点T作直线TM⊥OC,垂足为点M,且M在线段OC上(不与O、C重合),过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中,为常数,试确定k的值.
【解答】解:(1)∵二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1,
则有解得
∴二次函数y=x2﹣2x,
(2)由(1)得,B(1,﹣1),
∵A(﹣1,3),
∴直线AB解析式为y=﹣2x+1,AB=2,
设点Q(m,0),P(n,n2﹣2n)
∵以A、B、P、Q为顶点的四边形是平行四边形,
①当AB为对角线时,根据中点坐标公式得,则有,解得或
∴P(1+,2)和(1﹣,2)
②当AB为边时,根据中点坐标公式得解得或
∴P(1+,4)或(1﹣,4).
(3)设T(m,m2﹣2m),∵TM⊥OC,
∴可以设直线TM为y=﹣x+b,则m2﹣2m=﹣m+b,b=m2﹣2m+,
由解得,
∴OM==,ON=m?,
∴=,
∴k=时, =.
∴当k=时,点T运动的过程中,为常数.
14、如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(1)用含m的代数式表示BE的长.
(2)当m=时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
【解答】解:(1)∵C(0,﹣3),AC⊥OC,
∴点A纵坐标为﹣3,
y=﹣3时,﹣3=x2﹣mx﹣3,解得x=0或m,
∴点A坐标(m,﹣3),
∴AC=m,
∴BE=2AC=2m.
(2)∵m=,
∴点A坐标(,﹣3),
∴直线OA为y=﹣x,
∴抛物线解析式为y=x2﹣x﹣3,
∴点B坐标(2,3),
∴点D纵坐标为3,
对于函数y=﹣x,当y=3时,x=﹣,
∴点D坐标(﹣,3).
∵对于函数y=x2﹣x﹣3,x=﹣时,y=3,
∴点D在落在抛物线上.
(3)①∵∠ACE=∠CEG=∠EGA=90°,
∴四边形ECAG是矩形,
∴EG=AC=BG,
∵FG∥OE,
∴OF=FB,∵EG=BG,
∴EO=2FG,
∵?DE?EO=?GB?GF,
∴BG=2DE,
∵DE∥AC,
∴==,
∵点B坐标(2m,2m2﹣3),
∴OC=2OE,
∴3=2(2m2﹣3),
∵m>0,
∴m=.
②∵A(m,﹣3),B(2m,2m2﹣3),E(0,2m2﹣3),
∴直线AE解析式为y=﹣2mx+2m2﹣3,直线OB解析式为y=x,
由消去y得到﹣2mx+2m2﹣3=x,解得x=,
∴点M横坐标为,
∵△AMF的面积=△BFG的面积,
∴?(+3)?(m﹣)=?m??(2m2﹣3),
整理得到:2m4﹣9m2=0,
∵m>0,
∴m=.
故答案为.
15、抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,-3)、B(4,0),
① 求该抛物线的解析式;
② 若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2) 如图2,已知直线PA、PB与y轴分别交于E、F两点.当点P运动时,是否为定值?若是,试求出该定值;若不是,请说明理由.【来源:21·世纪·教育·网】
【答案】 (1)①y=x2-;②点D的坐标为(-1,-3)或(,);(2)是定值,等于2
【解析】解:(1)①将P(1,-3)、B(4,0)代入y=ax2+c得
,解得 ,抛物线的解析式为: .
②如图:
由∠DPO=∠POB得DP∥OB,D与P关于y轴对称,P(1,-3)得D(-1,-3);
如图,D在P右侧,即图中D2,则∠D2PO=∠POB,延长PD2交x轴于Q,则QO=QP,
设Q(q,0),则(q-1)2+32=q2,解得:q=5,∴Q(5,0),则直线PD2为 ,再联立 得:x=1或 ,∴ D2( )www-2-1-cnjy-com
∴点D的坐标为(-1,-3)或( )
(2)设B(b,0),则A(-b,0)有ab2+c=0,∴b2=,过点P(x0,y0)作PH⊥AB,有,易证:△PAH∽△EAO,则 即,∴,
同理得∴,∴,则OE+OF=
∴,又OC=-c,∴.
∴是定值,等于2.
16、如图,在平面直角坐标系xOy中,将二次函数y=x2﹣1的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
(1)求N的函数表达式;
(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求PA2+PB2的最大值;
(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.
【解答】(1)解:二次函数y=x2﹣1的图象M沿x轴翻折得到函数的解析式为y=﹣x2+1,此时顶点坐标(0,1),
将此图象向右平移2个单位长度后再向上平移8个单位长度得到二次函数图象N的顶点为(2,9),
故N的函数表达式y=﹣(x﹣2)2+9=﹣x2+4x+5.
(2)∵A(﹣1,0),B(1,0),
∴PA2+PB2=(m+1)2+n2+(m﹣1)2+n2=2(m2+n2)+2=2PO2+2,
∴当PO最大时PA2+PB2最大.如图,延长OC与⊙O交于点P,此时OP最大,
∴OP的最大值=OC+PO=+1,
∴PA2+PB2最大值=2(+1)2+2=38+4.
(3)M与N所围成封闭图形如图所示,
由图象可知,M与N所围成封闭图形内(包括边界)整点的个数为25个.
17、已知抛物线与x轴交于A(6,0)、B(﹣,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.21教育网
(1)求此抛物线的解析式;
(2)如图1,将△OMN沿x轴向右平移t个单位(0≤t≤5)到△O′M′N′的位置,MN′、M′O′与直线AC分别交于点E、F.
①当点F为M′O′的中点时,求t的值;
②如图2,若直线M′N′与抛物线相交于点G,过点G作GH∥M′O′交AC于点H,试确定线段EH是否存在最大值?若存在,求出它的最大值及此时t的值;若不存在,请说明理由.
【解答】解:(1)设抛物线解析式为y=a(x﹣6)(x+),把点M(1,3)代入得a=﹣,
∴抛物线解析式为y=﹣(x﹣6)(x+),
∴y=﹣x2+x+2.
(2)①如图1中,AC与OM交于点G.连接EO′.
∵AO=6,OC=2,MN=3,ON=1,
∴==3,
∴=,∵∠AOC=∠MON=90°,
∴△AOC∽△MNO,
∴∠OAC=∠NMO,
∵∠NMO+∠MON=90°,
∴∠MON+∠OAC=90°,
∴∠AGO=90°,
∴OM⊥AC,
∵△M′N′O′是由△MNO平移所得,
∴O′M′∥OM,
∴O′M′⊥AC,
∵M′F=FO′,
∴EM′=EO′,
∵EN′∥CO,
∴=,
∴=,
∴EN′=(5﹣t),
在RT△EO′M′中,∵O′N′=1,EN′=(5﹣t),EO′=EM′=+t,
∴(+t)2=1+(﹣t)2,
∴t=1.
②如图2中,
∵GH∥O′M′,O′M′⊥AC,
∴GH⊥AC,
∴∠GHE=90°,
∵∠EGH+∠HEG=90°,∠AEN′+∠OAC=90°,∠HEG=∠AEN′,
∴∠OAC=∠HGE,∵∠GHE=∠AOC=90°,
∴△GHE∽△AOC,
∴==,
∴EG最大时,EH最大,
∵EG=GN′﹣EN′=﹣(t+1)2+(t+1)+2﹣(5﹣t)=﹣t2+t+=﹣(t﹣2)2+.
∴t=2时,EG最大值=,
∴EH最大值=.
∴t=2时,EH最大值为.
18、如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
【解答】解:
(1)把B、C两点坐标代入抛物线解析式可得,解得,
∴抛物线解析式为y=x2﹣2x﹣3;
(2)如图1,连接BC,过Py轴的平行线,交BC于点M,交x轴于点H,
在y=x2﹣2x﹣3中,令y=0可得0=x2﹣2x﹣3,解得x=﹣1或x=3,
∴A点坐标为(﹣1,0),
∴AB=3﹣(﹣1)=4,且OC=3,
∴S△ABC=AB?OC=×4×3=6,
∵B(3,0),C(0,﹣3),
∴直线BC解析式为y=x﹣3,
设P点坐标为(x,x2﹣2x﹣3),则M点坐标为(x,x﹣3),
∵P点在第四限,
∴PM=x﹣3﹣(x2﹣2x﹣3)=﹣x2+3x,
∴S△PBC=PM?OH+PM?HB=PM?(OH+HB)=PM?OB=PM,
∴当PM有最大值时,△PBC的面积最大,则四边形ABPC的面积最大,
∵PM=﹣x2+3x=﹣(x﹣)2+,
∴当x=时,PMmax=,则S△PBC=×=,
此时P点坐标为(,﹣),S四边形ABPC=S△ABC+S△PBC=6+=,
即当P点坐标为(,﹣)时,四边形ABPC的面积最大,最大面积为;
(3)如图2,设直线m交y轴于点N,交直线l于点G,
则∠AGP=∠GNC+∠GCN,
当△AGB和△NGC相似时,必有∠AGB=∠CGB,
又∠AGB+∠CGB=180°,
∴∠AGB=∠CGB=90°,
∴∠ACO=∠OBN,
在Rt△AON和Rt△NOB中
∴Rt△AON≌Rt△NOB(ASA),
∴ON=OA=1,
∴N点坐标为(0,﹣1),
设直线m解析式为y=kx+d,把B、N两点坐标代入可得,解得,
∴直线m解析式为y=x﹣1,
即存在满足条件的直线m,其解析式为y=x﹣1.
班级 姓名
选择题
1、二次函数y=ax2+bx+c(a,b,c为常数且a≠0)的图象如图所示,则一次函数y=ax+b与反比例函数y=的图象可能是( )【出处:21教育名师】
A. B. C. D.
2、如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )21教育名师原创作品
A.一直减小 B.一直不变 C.先减小后增大 D.先增大后减小
3、已知二次函数y=x2+bx+c与x轴只有一个交点,且图象过A(x1,m)、B(x1+n,m)两点,则m、n的关系为( )
A.m=n B.m=n C.m=n2 D.m=n2
4、如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )
A.2a﹣b=0
B.a+b+c>0
C.3a﹣c=0
D.当a=时,△ABD是等腰直角三角形
5、已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )
A. B. C. D.2
6、已知a≥2,m2﹣2am+2=0,n2﹣2an+2=0,则(m﹣1)2+(n﹣1)2的最小值是( )
A.6 B.3 C.﹣3 D.0
7、若二次函数y=ax2﹣2ax+c的图象经过点(﹣1,0),则方程ax2﹣2ax+c=0的解为( )
A.x1=﹣3,x2=﹣1 B.x1=1,x2=3 C.x1=﹣1,x2=3 D.x1=﹣3,x2=1
8、在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
A.y1<y2 B.y1>y2 C.y的最小值是﹣3 D.y的最小值是﹣4
二、填空题
9、设x1、x2是方程5x2﹣3x﹣2=0的两个实数根,则+的值为 .
10、已知抛物线y=ax2+bx+c开口向上且经过点(1,1),双曲线y=经过点(a,bc),给出下列结论:①bc>0;②b+c>0;③b,c是关于x的一元二次方程x2+(a﹣1)x+=0的两个实数根;④a﹣b﹣c≥3.其中正确结论是 (填写序号)
解答题
11、二次函数的图象经过点(4,3),(3,0)。
(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴;
(3)在所给坐标系中画出二次函数的图象。
12、如图,抛物线y=x2﹣3x+与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标.
13、如图1,二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1.
(1)求这个二次函数的表达式;
(2)点P在该二次函数的图象上,点Q在x轴上,若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;
(3)如图3,一次函数y=kx(k>0)的图象与该二次函数的图象交于O、C两点,点T为该二次函数图象上位于直线OC下方的动点,过点T作直线TM⊥OC,垂足为点M,且M在线段OC上(不与O、C重合),过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中,为常数,试确定k的值.
14、如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(1)用含m的代数式表示BE的长.
(2)当m=时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
15、抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,-3)、B(4,0),
① 求该抛物线的解析式;
② 若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2) 如图2,已知直线PA、PB与y轴分别交于E、F两点.当点P运动时,是否为定值?若是,试求出该定值;若不是,请说明理由.21世纪教育网版权所有
16、如图,在平面直角坐标系xOy中,将二次函数y=x2﹣1的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N. 21cnjy.com
(1)求N的函数表达式;
(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求PA2+PB2的最大值;
(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数. 21·世纪*教育网
17、已知抛物线与x轴交于A(6,0)、B(﹣,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.【版权所有:21教育】
(1)求此抛物线的解析式;
(2)如图1,将△OMN沿x轴向右平移t个单位(0≤t≤5)到△O′M′N′的位置,MN′、M′O′与直线AC分别交于点E、F.21*cnjy*com
①当点F为M′O′的中点时,求t的值;
②如图2,若直线M′N′与抛物线相交于点G,过点G作GH∥M′O′交AC于点H,试确定线段EH是否存在最大值?若存在,求出它的最大值及此时t的值;若不存在,请说明理由.
18、如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)2-1-c-n-j-y
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
二次函数重难点专题训练卷(2)
答案详解
一、选择题
2、如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )www.21-cn-jy.com
A.一直减小 B.一直不变 C.先减小后增大 D.先增大后减小
【解答】解:在RT△ABC中,∵∠ACB=90°,AC=4,BC=2,
∴AB===2,设PD=x,AB边上的高为h,
h==,
∵PD∥BC,
∴=,
∴AD=2x,AP=x,
∴S1+S2=?2x?x+(2﹣1﹣x)?=x2﹣2x+4﹣=(x﹣1)2+3﹣,
∴当0<x<1时,S1+S2的值随x的增大而减小,
当1≤x≤2时,S1+S2的值随x的增大而增大.
故选C.
3、已知二次函数y=x2+bx+c与x轴只有一个交点,且图象过A(x1,m)、B(x1+n,m)两点,则m、n的关系为( )2·1·c·n·j·y
A.m=n B.m=n C.m=n2 D.m=n2
【解答】解:∵抛物线y=x2+bx+c与x轴只有一个交点,
∴当x=﹣时,y=0.且b2﹣4c=0,即b2=4c.
又∵点A(x1,m),B(x1+n,m),
∴点A、B关于直线x=﹣对称,
∴A(﹣﹣,m),B(﹣+,m),
将A点坐标代入抛物线解析式,得m=(﹣﹣)2+(﹣﹣)b+c,即m=﹣+c,
∵b2=4c,
∴m=n2,
故选D.
4、如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )【来源:21cnj*y.co*m】
A.2a﹣b=0
B.a+b+c>0
C.3a﹣c=0
D.当a=时,△ABD是等腰直角三角形
【解答】解:∵抛物线与x轴的交点A、B的横坐标分别为﹣1,3,
∴抛物线的对称轴为直线x=1,则﹣=1,
∴2a+b=0,
∴选项A错误;
∴当自变量取1时,对应的函数图象在x轴下方,
∴x=1时,y<0,则a+b+c<0,
∴选项B错误;
∵A点坐标为(﹣1,0),
∴a﹣b+c=0,而b=﹣2a,
∴a+2a+c=0,
∴3a+c=0,
∴选项C错误;
当a=,则b=﹣1,c=﹣,对称轴x=1与x轴的交点为E,如图,
∴抛物线的解析式为y=x2﹣x﹣,
把x=1代入得y=﹣1﹣=﹣2,
∴D点坐标为(1,﹣2),
∴AE=2,BE=2,DE=2,
∴△ADE和△BDE都为等腰直角三角形,
∴△ADB为等腰直角三角形,
∴选项D正确.
故选D.
5、已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )
A. B. C. D.2
【解答】解:令y=0,则﹣x2﹣2x+3=0,解得x=﹣3或1,不妨设A(﹣3,0),B(1,0),
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点C(﹣1,4),
如图所示,作CD⊥AB于D.
在RT△ACD中,tan∠CAD===2,
故答案为D.
6、已知a≥2,m2﹣2am+2=0,n2﹣2an+2=0,则(m﹣1)2+(n﹣1)2的最小值是( )
A.6 B.3 C.﹣3 D.0
【解答】解:∵m2﹣2am+2=0,n2﹣2an+2=0,
∴m,n是关于x的方程x2﹣2ax+2=0的两个根,
∴m+n=2a,mn=2,
∴(m﹣1)2+(n﹣1)2=m2﹣2m+1+n2﹣2n+1=(m+n)2﹣2mn﹣2(m+n)+2=4a2﹣4﹣4a+2=4(a﹣)2﹣3,
∵a≥2,
∴当a=2时,(m﹣1)2+(n﹣1)2有最小值,
∴(m﹣1)2+(n﹣1)2的最小值=4(a﹣)2+3=4(2﹣)2﹣3=6,
故选A.
7、若二次函数y=ax2﹣2ax+c的图象经过点(﹣1,0),则方程ax2﹣2ax+c=0的解为( )
A.x1=﹣3,x2=﹣1 B.x1=1,x2=3 C.x1=﹣1,x2=3 D.x1=﹣3,x2=1
【解答】解:∵二次函数y=ax2﹣2ax+c的图象经过点(﹣1,0),
∴方程ax2﹣2ax+c=0一定有一个解为:x=﹣1,
∵抛物线的对称轴为:直线x=1,
∴二次函数y=ax2﹣2ax+c的图象与x轴的另一个交点为:(3,0),
∴方程ax2﹣2ax+c=0的解为:x1=﹣1,x2=3.
故选:C.
8、在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
A.y1<y2 B.y1>y2 C.y的最小值是﹣3 D.y的最小值是﹣4
【解答】解:y=x2+2x﹣3=(x+3)(x﹣1),
则该抛物线与x轴的两交点横坐标分别是﹣3、1.
又y=x2+2x﹣3=(x+1)2﹣4,
∴该抛物线的顶点坐标是(﹣1,﹣4),对称轴为x=﹣1.
A、无法确定点A、B离对称轴x=﹣1的远近,故无法判断y1与y2的大小,故本选项错误;
B、无法确定点A、B离对称轴x=﹣1的远近,故无法判断y1与y2的大小,故本选项错误;
C、y的最小值是﹣4,故本选项错误;
D、y的最小值是﹣4,故本选项正确.
故选:D.
二、填空题
9、设x1、x2是方程5x2﹣3x﹣2=0的两个实数根,则+的值为 ﹣ .
【解答】解:∵方程x1、x2是方程5x2﹣3x﹣2=0的两个实数根,
∴x1+x2=,x1x2=﹣,
∴+===﹣.
故答案为:﹣.
10、已知抛物线y=ax2+bx+c开口向上且经过点(1,1),双曲线y=经过点(a,bc),给出下列结论:①bc>0;②b+c>0;③b,c是关于x的一元二次方程x2+(a﹣1)x+=0的两个实数根;④a﹣b﹣c≥3.其中正确结论是 ①③ (填写序号)
【解答】解:∵抛物线y=ax2+bx+c开口向上且经过点(1,1),双曲线y=经过点(a,bc), 21*cnjy*com
∴
∴bc>0,故①正确;
∴a>1时,则b、c均小于0,此时b+c<0,
当a=1时,b+c=0,则与题意矛盾,
当0<a<1时,则b、c均大于0,此时b+c>0,
故②错误;
∴x2+(a﹣1)x+=0可以转化为:x2+(b+c)x+bc=0,得x=b或x=c,故③正确;
∵b,c是关于x的一元二次方程x2+(a﹣1)x+=0的两个实数根,
∴a﹣b﹣c=a﹣(b+c)=a+(a﹣1)=2a﹣1,
当a>1时,2a﹣1>3,
当0<a<1时,﹣1<2a﹣1<3,
故④错误;
故答案为:①③.
解答题
11、二次函数的图象经过点(4,3),(3,0)。
(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴;
(3)在所给坐标系中画出二次函数的图象。
【解答】 解:(1)∵二次函数的图象经过点(4,3),(3,0),
∴,解得。
(2)∵该二次函数为。
∴该二次函数图象的顶点坐标为(2,-1),对称轴为x=1。
(3)列表如下:
x
···
0
1
2
3
4
···
y
···
3
0
1
0
3
···
描点作图如下:
12、如图,抛物线y=x2﹣3x+与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标.
【解答】解:(1)∵抛物线y=x2﹣3x+与x轴相交于A、B两点,与y轴相交于点C,
∴令y=0,可得x=或x=,
∴A(,0),B(,0);
令x=0,则y=,
∴C点坐标为(0,),
设直线BC的解析式为:y=kx+b,则有,
,
解得:,
∴直线BC的解析式为:y=x;
(2)设点D的横坐标为m,则纵坐标为(m,),
∴E点的坐标为(m, m),
设DE的长度为d,
∵点D是直线BC下方抛物线上一点,
则d=m+﹣(m2﹣3m+),
整理得,d=﹣m2+m,
∵a=﹣1<0,
∴当m==时,d最大===,
∴D点的坐标为(,).
13、如图1,二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1.
(1)求这个二次函数的表达式;
(2)点P在该二次函数的图象上,点Q在x轴上,若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;21·cn·jy·com
(3)如图3,一次函数y=kx(k>0)的图象与该二次函数的图象交于O、C两点,点T为该二次函数图象上位于直线OC下方的动点,过点T作直线TM⊥OC,垂足为点M,且M在线段OC上(不与O、C重合),过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中,为常数,试确定k的值.
【解答】解:(1)∵二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1,
则有解得
∴二次函数y=x2﹣2x,
(2)由(1)得,B(1,﹣1),
∵A(﹣1,3),
∴直线AB解析式为y=﹣2x+1,AB=2,
设点Q(m,0),P(n,n2﹣2n)
∵以A、B、P、Q为顶点的四边形是平行四边形,
①当AB为对角线时,根据中点坐标公式得,则有,解得或
∴P(1+,2)和(1﹣,2)
②当AB为边时,根据中点坐标公式得解得或
∴P(1+,4)或(1﹣,4).
(3)设T(m,m2﹣2m),∵TM⊥OC,
∴可以设直线TM为y=﹣x+b,则m2﹣2m=﹣m+b,b=m2﹣2m+,
由解得,
∴OM==,ON=m?,
∴=,
∴k=时, =.
∴当k=时,点T运动的过程中,为常数.
14、如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(1)用含m的代数式表示BE的长.
(2)当m=时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
【解答】解:(1)∵C(0,﹣3),AC⊥OC,
∴点A纵坐标为﹣3,
y=﹣3时,﹣3=x2﹣mx﹣3,解得x=0或m,
∴点A坐标(m,﹣3),
∴AC=m,
∴BE=2AC=2m.
(2)∵m=,
∴点A坐标(,﹣3),
∴直线OA为y=﹣x,
∴抛物线解析式为y=x2﹣x﹣3,
∴点B坐标(2,3),
∴点D纵坐标为3,
对于函数y=﹣x,当y=3时,x=﹣,
∴点D坐标(﹣,3).
∵对于函数y=x2﹣x﹣3,x=﹣时,y=3,
∴点D在落在抛物线上.
(3)①∵∠ACE=∠CEG=∠EGA=90°,
∴四边形ECAG是矩形,
∴EG=AC=BG,
∵FG∥OE,
∴OF=FB,∵EG=BG,
∴EO=2FG,
∵?DE?EO=?GB?GF,
∴BG=2DE,
∵DE∥AC,
∴==,
∵点B坐标(2m,2m2﹣3),
∴OC=2OE,
∴3=2(2m2﹣3),
∵m>0,
∴m=.
②∵A(m,﹣3),B(2m,2m2﹣3),E(0,2m2﹣3),
∴直线AE解析式为y=﹣2mx+2m2﹣3,直线OB解析式为y=x,
由消去y得到﹣2mx+2m2﹣3=x,解得x=,
∴点M横坐标为,
∵△AMF的面积=△BFG的面积,
∴?(+3)?(m﹣)=?m??(2m2﹣3),
整理得到:2m4﹣9m2=0,
∵m>0,
∴m=.
故答案为.
15、抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,-3)、B(4,0),
① 求该抛物线的解析式;
② 若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2) 如图2,已知直线PA、PB与y轴分别交于E、F两点.当点P运动时,是否为定值?若是,试求出该定值;若不是,请说明理由.【来源:21·世纪·教育·网】
【答案】 (1)①y=x2-;②点D的坐标为(-1,-3)或(,);(2)是定值,等于2
【解析】解:(1)①将P(1,-3)、B(4,0)代入y=ax2+c得
,解得 ,抛物线的解析式为: .
②如图:
由∠DPO=∠POB得DP∥OB,D与P关于y轴对称,P(1,-3)得D(-1,-3);
如图,D在P右侧,即图中D2,则∠D2PO=∠POB,延长PD2交x轴于Q,则QO=QP,
设Q(q,0),则(q-1)2+32=q2,解得:q=5,∴Q(5,0),则直线PD2为 ,再联立 得:x=1或 ,∴ D2( )www-2-1-cnjy-com
∴点D的坐标为(-1,-3)或( )
(2)设B(b,0),则A(-b,0)有ab2+c=0,∴b2=,过点P(x0,y0)作PH⊥AB,有,易证:△PAH∽△EAO,则 即,∴,
同理得∴,∴,则OE+OF=
∴,又OC=-c,∴.
∴是定值,等于2.
16、如图,在平面直角坐标系xOy中,将二次函数y=x2﹣1的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
(1)求N的函数表达式;
(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求PA2+PB2的最大值;
(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.
【解答】(1)解:二次函数y=x2﹣1的图象M沿x轴翻折得到函数的解析式为y=﹣x2+1,此时顶点坐标(0,1),
将此图象向右平移2个单位长度后再向上平移8个单位长度得到二次函数图象N的顶点为(2,9),
故N的函数表达式y=﹣(x﹣2)2+9=﹣x2+4x+5.
(2)∵A(﹣1,0),B(1,0),
∴PA2+PB2=(m+1)2+n2+(m﹣1)2+n2=2(m2+n2)+2=2PO2+2,
∴当PO最大时PA2+PB2最大.如图,延长OC与⊙O交于点P,此时OP最大,
∴OP的最大值=OC+PO=+1,
∴PA2+PB2最大值=2(+1)2+2=38+4.
(3)M与N所围成封闭图形如图所示,
由图象可知,M与N所围成封闭图形内(包括边界)整点的个数为25个.
17、已知抛物线与x轴交于A(6,0)、B(﹣,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.21教育网
(1)求此抛物线的解析式;
(2)如图1,将△OMN沿x轴向右平移t个单位(0≤t≤5)到△O′M′N′的位置,MN′、M′O′与直线AC分别交于点E、F.
①当点F为M′O′的中点时,求t的值;
②如图2,若直线M′N′与抛物线相交于点G,过点G作GH∥M′O′交AC于点H,试确定线段EH是否存在最大值?若存在,求出它的最大值及此时t的值;若不存在,请说明理由.
【解答】解:(1)设抛物线解析式为y=a(x﹣6)(x+),把点M(1,3)代入得a=﹣,
∴抛物线解析式为y=﹣(x﹣6)(x+),
∴y=﹣x2+x+2.
(2)①如图1中,AC与OM交于点G.连接EO′.
∵AO=6,OC=2,MN=3,ON=1,
∴==3,
∴=,∵∠AOC=∠MON=90°,
∴△AOC∽△MNO,
∴∠OAC=∠NMO,
∵∠NMO+∠MON=90°,
∴∠MON+∠OAC=90°,
∴∠AGO=90°,
∴OM⊥AC,
∵△M′N′O′是由△MNO平移所得,
∴O′M′∥OM,
∴O′M′⊥AC,
∵M′F=FO′,
∴EM′=EO′,
∵EN′∥CO,
∴=,
∴=,
∴EN′=(5﹣t),
在RT△EO′M′中,∵O′N′=1,EN′=(5﹣t),EO′=EM′=+t,
∴(+t)2=1+(﹣t)2,
∴t=1.
②如图2中,
∵GH∥O′M′,O′M′⊥AC,
∴GH⊥AC,
∴∠GHE=90°,
∵∠EGH+∠HEG=90°,∠AEN′+∠OAC=90°,∠HEG=∠AEN′,
∴∠OAC=∠HGE,∵∠GHE=∠AOC=90°,
∴△GHE∽△AOC,
∴==,
∴EG最大时,EH最大,
∵EG=GN′﹣EN′=﹣(t+1)2+(t+1)+2﹣(5﹣t)=﹣t2+t+=﹣(t﹣2)2+.
∴t=2时,EG最大值=,
∴EH最大值=.
∴t=2时,EH最大值为.
18、如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
【解答】解:
(1)把B、C两点坐标代入抛物线解析式可得,解得,
∴抛物线解析式为y=x2﹣2x﹣3;
(2)如图1,连接BC,过Py轴的平行线,交BC于点M,交x轴于点H,
在y=x2﹣2x﹣3中,令y=0可得0=x2﹣2x﹣3,解得x=﹣1或x=3,
∴A点坐标为(﹣1,0),
∴AB=3﹣(﹣1)=4,且OC=3,
∴S△ABC=AB?OC=×4×3=6,
∵B(3,0),C(0,﹣3),
∴直线BC解析式为y=x﹣3,
设P点坐标为(x,x2﹣2x﹣3),则M点坐标为(x,x﹣3),
∵P点在第四限,
∴PM=x﹣3﹣(x2﹣2x﹣3)=﹣x2+3x,
∴S△PBC=PM?OH+PM?HB=PM?(OH+HB)=PM?OB=PM,
∴当PM有最大值时,△PBC的面积最大,则四边形ABPC的面积最大,
∵PM=﹣x2+3x=﹣(x﹣)2+,
∴当x=时,PMmax=,则S△PBC=×=,
此时P点坐标为(,﹣),S四边形ABPC=S△ABC+S△PBC=6+=,
即当P点坐标为(,﹣)时,四边形ABPC的面积最大,最大面积为;
(3)如图2,设直线m交y轴于点N,交直线l于点G,
则∠AGP=∠GNC+∠GCN,
当△AGB和△NGC相似时,必有∠AGB=∠CGB,
又∠AGB+∠CGB=180°,
∴∠AGB=∠CGB=90°,
∴∠ACO=∠OBN,
在Rt△AON和Rt△NOB中
∴Rt△AON≌Rt△NOB(ASA),
∴ON=OA=1,
∴N点坐标为(0,﹣1),
设直线m解析式为y=kx+d,把B、N两点坐标代入可得,解得,
∴直线m解析式为y=x﹣1,
即存在满足条件的直线m,其解析式为y=x﹣1.
同课章节目录
