教科版八上物理第1章 走进实验室《3.活动:降落伞比赛》课件 (共32张PPT)
文档属性
| 名称 | 教科版八上物理第1章 走进实验室《3.活动:降落伞比赛》课件 (共32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-10-16 00:00:00 | ||
图片预览











文档简介
(共32张PPT)
活动:降落伞比赛
自制降落伞进行比赛
同学们想一想降落伞在空间滞留的时间与哪些因素有关?
可能与降落伞的形状有关
可能与降落伞的面积有关
可能与降落伞的伞绳有关
还与哪些因素有关呢?
比赛我们采用“控制变量法”。
控制变量法:在多个
变量同时存在的物理实验
中,我们通常采用的只改
变其中一个变量,而其余
变量均保持不变探究其物
理变化规律的方法。
控制变量法
“一变余不变”
1. 是否与降落伞的形状有关?
要求:保持降落伞的其他条件不变,将伞面分别做成长方形、正方形和圆形,做好后让他们从同一高度下落,记录伞在空中停留的时间,比较三种伞哪个空中停留的时间长。
提出猜测
2. 是否与降落伞的面积有关?
要求:保持其他条件不变,只改变伞面的大小,测量并计算出每次伞面的面积,然后将做好的降落伞从同一高度下落,记录每种情况在空中停留的时间,然后比较。
3. 是否与降落伞的伞绳有关?
要求:保持其他条件不变,只改变伞绳的长短,然后让降落伞从同一高度下落,记录每次空中停留的时间,然后比较长短。
4. 是否与伞的高度有关?
要求:保持其他条件不变,让伞从不同高度下落,记录每次在空中停留的时间,然后比较长短。
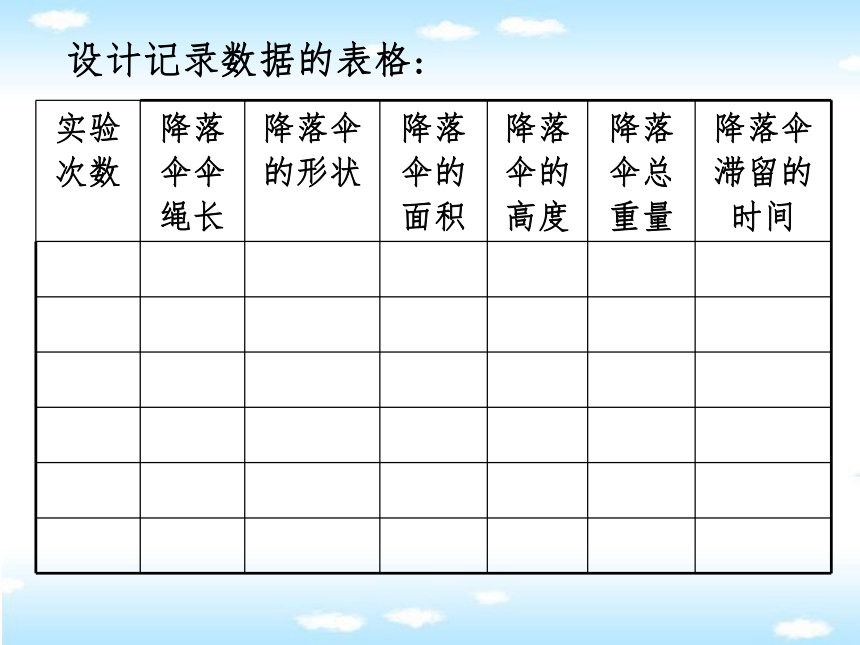
设计记录数据的表格:
实验次数 降落伞伞绳长 降落伞的形状 降落伞的面积 降落伞的高度 降落伞总重量 降落伞滞留的时间
实验数据记录:
实验次数 降落伞伞绳长 降落伞的形状 降落伞的面积 降落伞的高度 降落伞总重量 降落伞滞留的时间
1 1m 圆形 0.5m2 3m 20g 3.67s
2 1m 圆形 1m2 3m 20g 5.82s
3 1m 圆形 1m2 3m 30g 4.91s
4 1m 正方形 1m2 3m 20g 5.81s
5 1.5m 正方形 1m2 3m 20g 5.83s
6 1.5m 正方形 1m2 6m 20g 9.24s
实验数据分析:
实验次数 降落伞伞绳长 降落伞的形状 降落伞的面积 降落伞的高度 降落伞总重量 降落伞滞留的时间
1 1m 圆形 0.5m2 3m 20g 3.67s
2 1m 圆形 1m2 3m 20g 5.82s
3 1m 圆形 1m2 3m 30g 4.91s
4 1m 正方形 1m2 3m 20g 5.81s
5 1.5m 正方形 1m2 3m 20g 5.83s
6 1.5m 正方形 1m2 6m 20g 9.24s
比较(1) (2)两组数据,可知在其它条件一定的情况下,
降落伞在空中滞留的时间与伞的面积有关,伞的面积越大,
伞在空中滞留的时间越长。
实验数据分析:
实验次数 降落伞伞绳长 降落伞的形状 降落伞的面积 降落伞的高度 降落伞总重量 降落伞滞留的时间
1 1m 圆形 0.5m2 3m 20g 3.67s
2 1m 圆形 1m2 3m 20g 5.82s
3 1m 圆形 1m2 3m 30g 4.91s
4 1m 正方形 1m2 3m 20g 5.81s
5 1.5m 正方形 1m2 3m 20g 5.83s
6 1.5m 正方形 1m2 6m 20g 9.24s
比较⑵和⑶两组数据可知:在其它条件一定的情况下,
降落伞在空中滞留的时间与伞的总重量有关,伞的总重量
越大,伞在空中滞留的时间越短。
实验数据分析:
实验次数 降落伞伞绳长 降落伞的形状 降落伞的面积 降落伞的高度 降落伞总重量 降落伞滞留的时间
1 1m 圆形 0.5m2 3m 20g 3.67s
2 1m 圆形 1m2 3m 20g 5.82s
3 1m 圆形 1m2 3m 30g 4.91s
4 1m 正方形 1m2 3m 20g 5.81s
5 1.5m 正方形 1m2 3m 20g 5.83s
6 1.5m 正方形 1m2 6m 20g 9.24s
比较⑵和⑷两组数据可知在其它条件一定的情况下,
降落伞在空中滞留的时间与伞的形状无关:
实验数据分析:
实验次数 降落伞伞绳长 降落伞的形状 降落伞的面积 降落伞的高度 降落伞总重量 降落伞滞留的时间
1 1m 圆形 0.5m2 3m 20g 3.67s
2 1m 圆形 1m2 3m 20g 5.82s
3 1m 圆形 1m2 3m 30g 4.91s
4 1m 正方形 1m2 3m 20g 5.81s
5 1.5m 正方形 1m2 3m 20g 5.83s
6 1.5m 正方形 1m2 6m 20g 9.24s
比较⑷和⑸两组数据可知:在其它条件一定的情况下,
降落伞在空中滞留的时间与伞的伞绳长无关。
实验数据记录:
实验次数 降落伞伞绳长 降落伞的形状 降落伞的面积 降落伞的高度 降落伞总重量 降落伞滞留的时间
1 1m 圆形 0.5m2 3m 20g 3.67s
2 1m 圆形 1m2 3m 20g 5.82s
3 1m 圆形 1m2 3m 30g 4.91s
4 1m 正方形 1m2 3m 20g 5.81s
5 1.5m 正方形 1m2 3m 20g 5.83s
6 1.5m 正方形 1m2 6m 20g 9.24s
比较⑸和⑹两组数据可知:在其它条件一定的情况下,降落伞
在空中滞留的时间与伞高度有关,伞的高度越高,伞在空中滞留的
时间越长。
学习通过实验可以得出如下结论:
相关因素
面积
高度
伞的面积越大,在空中停留的时间越长
伞的高度越高,在空中停留的时间越长
无关因素
形状
绳长
选择什么仪器对变量进行测量呢?
如何进行测量呢?
使用仪器的规程进行如下
①选择量程:量程是中学物理实验选择仪器的重要依据。若所选量程太小,不仅难以测量所测值,甚至可能会损坏仪器。如果所选量程太大,其相应的分度值一般也会较大,测量的误差也就大了。
②调节零点:测量仪器使用前,一般应先调整指针到零刻度,这个过程叫调零。如不能调零,要记录初始读数,进行修正。
③测量:读数时,要求眼睛正视刻度,记录数据,要实事求是。仪器读数一般要求读到分度值的十分之一,所以读数前要首先观看仪器的分度值。
④归整:实验完毕,要整理仪器,放回原处。
不规则面积的测量方法
我们在测量时常常会遇到不规则图形,如图所示.
我们可以把伞布放在方格纸上,在方格纸上描下它的轮廓,数一下图形中包含的方格数,对不满一格而大于半格的都算一格,小于半格的都不算。总的格数乘以一个格的面积,就是伞布的面积。
例题解析
【例l】在图中,(a)、(b)两图分别表示比较自行车和摩托车运动快慢的两种方法。
(a)图表明 .
(b)图表明 .
解:相同时间内,摩托车比自行车通过的路程长,所以摩托车快;通过相同的路程,摩托车比自行车所用的时间短,所以摩托车快
点拨:要比较两物体运动的快慢必须考虑时间与路程两个变量,图 (a)中控制了时间,图 (b)中控制了路程。本题是控制变量法在日常生活中的应用。
【例2 】下列过程经历的时间最接近1s的是 ( )
A.人步行10m所用的时间
B.人眨一下眼睛所用的时间
C.通常情况下人的心脏跳动一次所用的时间
D.朗读一首唐诗所用的时间
分析:世界百米冠军比赛时跑10m所用的时间约为1s,很显然,人步行10m所用的时间远远大于1s;人眨眼的时间很短暂,1s可以眨好几次眼;通常情况下人的心跳在每分钟70次左右,而一分钟为60s,故通常情况下人的心脏跳动一次所用的时间最接近1s;朗读一首唐诗所用的时间得用1、2min,也远远大于1s。
答案:C
【例3】体育老师想测量新修整过的学校操场的长度,请你帮老师从下面提供的器材中选择合适的测量工具( )
A.长为40cm,分度值为1mm的钢尺
B.长为1.5m,分度值为1mm的塑料尺 C.长为4m,分度值为1cm的钢卷尺
D.长为30m,分度值为1dm的皮卷尺
错解:A或B或C
错解分析:A、B两项的刻度尺,它们的量程、分度值、类型皆不合适。一般情况下,学校操场的长度为几百米,形状多为类椭圆形,利用A、B两项的刻度尺测量,不仅工作繁重且误差也比较大。C、D两项皆为卷尺,但它们的量程和分度值皆不相同,相较而言,显然D项更加合适。
正解:D
探究题
小芳同学观察到许多建筑材料的截面多是V形或U形,这引起了她的好奇心。
[提出问题]物体能够承受的压力的最大值与哪些因素有关
[猜想与假设]猜想一:物体能够承受的压力的最大值与物体的形状有关。
猜想二:物体能够承受的压力的最大值与物体的材料有关
[设计实验]小芳利用如图所示的装置,选取了纸条、细绳、火柴盒和若干火柴棒,对猜想一进行实验探究。
[进行实验与收集数据](1)选取材料和长、宽、厚相同的纸条若干。
(2)将一张纸条折成V形,放在装置上,在纸条两端距中点(支点)相同距离处,各挂一相同的火柴盒。在两端火柴盒中逐渐增加数量 的火柴棒,直到纸条被压弯折为止,将一端火柴盒中火柴棒的根数记录在下表中。
(3)将纸条分别折成U形、圆弧形,重复步骤(2).
(4)更换纸条,将以上实验再做两次。
[分析与论证]分析实验数据,可以得出的结论是(写出一条即可): .
[交流与合作](1)生产、生活中利用上述结论的事例很多,如巨大的铁桥中多处使用了U形钢材。请你举出一个利用V形或圆弧形结构的实例: 。
(2)若要探究猜想二,实验中应使所选物体的
和 相同。
解:[进行实验与收集数据] (2)相同
[分析与论证]完全相同的纸条,圆弧形纸条能够承受的压力最大(或物体能够承受的压力的最大值与形状有关)
[交流与合作](1)V形的有:厂房的屋架、塔吊支架;圆弧形的有:隧道顶、桥洞、拱形桥等(2)形状;长、宽、厚
活动:降落伞比赛
自制降落伞进行比赛
同学们想一想降落伞在空间滞留的时间与哪些因素有关?
可能与降落伞的形状有关
可能与降落伞的面积有关
可能与降落伞的伞绳有关
还与哪些因素有关呢?
比赛我们采用“控制变量法”。
控制变量法:在多个
变量同时存在的物理实验
中,我们通常采用的只改
变其中一个变量,而其余
变量均保持不变探究其物
理变化规律的方法。
控制变量法
“一变余不变”
1. 是否与降落伞的形状有关?
要求:保持降落伞的其他条件不变,将伞面分别做成长方形、正方形和圆形,做好后让他们从同一高度下落,记录伞在空中停留的时间,比较三种伞哪个空中停留的时间长。
提出猜测
2. 是否与降落伞的面积有关?
要求:保持其他条件不变,只改变伞面的大小,测量并计算出每次伞面的面积,然后将做好的降落伞从同一高度下落,记录每种情况在空中停留的时间,然后比较。
3. 是否与降落伞的伞绳有关?
要求:保持其他条件不变,只改变伞绳的长短,然后让降落伞从同一高度下落,记录每次空中停留的时间,然后比较长短。
4. 是否与伞的高度有关?
要求:保持其他条件不变,让伞从不同高度下落,记录每次在空中停留的时间,然后比较长短。
设计记录数据的表格:
实验次数 降落伞伞绳长 降落伞的形状 降落伞的面积 降落伞的高度 降落伞总重量 降落伞滞留的时间
实验数据记录:
实验次数 降落伞伞绳长 降落伞的形状 降落伞的面积 降落伞的高度 降落伞总重量 降落伞滞留的时间
1 1m 圆形 0.5m2 3m 20g 3.67s
2 1m 圆形 1m2 3m 20g 5.82s
3 1m 圆形 1m2 3m 30g 4.91s
4 1m 正方形 1m2 3m 20g 5.81s
5 1.5m 正方形 1m2 3m 20g 5.83s
6 1.5m 正方形 1m2 6m 20g 9.24s
实验数据分析:
实验次数 降落伞伞绳长 降落伞的形状 降落伞的面积 降落伞的高度 降落伞总重量 降落伞滞留的时间
1 1m 圆形 0.5m2 3m 20g 3.67s
2 1m 圆形 1m2 3m 20g 5.82s
3 1m 圆形 1m2 3m 30g 4.91s
4 1m 正方形 1m2 3m 20g 5.81s
5 1.5m 正方形 1m2 3m 20g 5.83s
6 1.5m 正方形 1m2 6m 20g 9.24s
比较(1) (2)两组数据,可知在其它条件一定的情况下,
降落伞在空中滞留的时间与伞的面积有关,伞的面积越大,
伞在空中滞留的时间越长。
实验数据分析:
实验次数 降落伞伞绳长 降落伞的形状 降落伞的面积 降落伞的高度 降落伞总重量 降落伞滞留的时间
1 1m 圆形 0.5m2 3m 20g 3.67s
2 1m 圆形 1m2 3m 20g 5.82s
3 1m 圆形 1m2 3m 30g 4.91s
4 1m 正方形 1m2 3m 20g 5.81s
5 1.5m 正方形 1m2 3m 20g 5.83s
6 1.5m 正方形 1m2 6m 20g 9.24s
比较⑵和⑶两组数据可知:在其它条件一定的情况下,
降落伞在空中滞留的时间与伞的总重量有关,伞的总重量
越大,伞在空中滞留的时间越短。
实验数据分析:
实验次数 降落伞伞绳长 降落伞的形状 降落伞的面积 降落伞的高度 降落伞总重量 降落伞滞留的时间
1 1m 圆形 0.5m2 3m 20g 3.67s
2 1m 圆形 1m2 3m 20g 5.82s
3 1m 圆形 1m2 3m 30g 4.91s
4 1m 正方形 1m2 3m 20g 5.81s
5 1.5m 正方形 1m2 3m 20g 5.83s
6 1.5m 正方形 1m2 6m 20g 9.24s
比较⑵和⑷两组数据可知在其它条件一定的情况下,
降落伞在空中滞留的时间与伞的形状无关:
实验数据分析:
实验次数 降落伞伞绳长 降落伞的形状 降落伞的面积 降落伞的高度 降落伞总重量 降落伞滞留的时间
1 1m 圆形 0.5m2 3m 20g 3.67s
2 1m 圆形 1m2 3m 20g 5.82s
3 1m 圆形 1m2 3m 30g 4.91s
4 1m 正方形 1m2 3m 20g 5.81s
5 1.5m 正方形 1m2 3m 20g 5.83s
6 1.5m 正方形 1m2 6m 20g 9.24s
比较⑷和⑸两组数据可知:在其它条件一定的情况下,
降落伞在空中滞留的时间与伞的伞绳长无关。
实验数据记录:
实验次数 降落伞伞绳长 降落伞的形状 降落伞的面积 降落伞的高度 降落伞总重量 降落伞滞留的时间
1 1m 圆形 0.5m2 3m 20g 3.67s
2 1m 圆形 1m2 3m 20g 5.82s
3 1m 圆形 1m2 3m 30g 4.91s
4 1m 正方形 1m2 3m 20g 5.81s
5 1.5m 正方形 1m2 3m 20g 5.83s
6 1.5m 正方形 1m2 6m 20g 9.24s
比较⑸和⑹两组数据可知:在其它条件一定的情况下,降落伞
在空中滞留的时间与伞高度有关,伞的高度越高,伞在空中滞留的
时间越长。
学习通过实验可以得出如下结论:
相关因素
面积
高度
伞的面积越大,在空中停留的时间越长
伞的高度越高,在空中停留的时间越长
无关因素
形状
绳长
选择什么仪器对变量进行测量呢?
如何进行测量呢?
使用仪器的规程进行如下
①选择量程:量程是中学物理实验选择仪器的重要依据。若所选量程太小,不仅难以测量所测值,甚至可能会损坏仪器。如果所选量程太大,其相应的分度值一般也会较大,测量的误差也就大了。
②调节零点:测量仪器使用前,一般应先调整指针到零刻度,这个过程叫调零。如不能调零,要记录初始读数,进行修正。
③测量:读数时,要求眼睛正视刻度,记录数据,要实事求是。仪器读数一般要求读到分度值的十分之一,所以读数前要首先观看仪器的分度值。
④归整:实验完毕,要整理仪器,放回原处。
不规则面积的测量方法
我们在测量时常常会遇到不规则图形,如图所示.
我们可以把伞布放在方格纸上,在方格纸上描下它的轮廓,数一下图形中包含的方格数,对不满一格而大于半格的都算一格,小于半格的都不算。总的格数乘以一个格的面积,就是伞布的面积。
例题解析
【例l】在图中,(a)、(b)两图分别表示比较自行车和摩托车运动快慢的两种方法。
(a)图表明 .
(b)图表明 .
解:相同时间内,摩托车比自行车通过的路程长,所以摩托车快;通过相同的路程,摩托车比自行车所用的时间短,所以摩托车快
点拨:要比较两物体运动的快慢必须考虑时间与路程两个变量,图 (a)中控制了时间,图 (b)中控制了路程。本题是控制变量法在日常生活中的应用。
【例2 】下列过程经历的时间最接近1s的是 ( )
A.人步行10m所用的时间
B.人眨一下眼睛所用的时间
C.通常情况下人的心脏跳动一次所用的时间
D.朗读一首唐诗所用的时间
分析:世界百米冠军比赛时跑10m所用的时间约为1s,很显然,人步行10m所用的时间远远大于1s;人眨眼的时间很短暂,1s可以眨好几次眼;通常情况下人的心跳在每分钟70次左右,而一分钟为60s,故通常情况下人的心脏跳动一次所用的时间最接近1s;朗读一首唐诗所用的时间得用1、2min,也远远大于1s。
答案:C
【例3】体育老师想测量新修整过的学校操场的长度,请你帮老师从下面提供的器材中选择合适的测量工具( )
A.长为40cm,分度值为1mm的钢尺
B.长为1.5m,分度值为1mm的塑料尺 C.长为4m,分度值为1cm的钢卷尺
D.长为30m,分度值为1dm的皮卷尺
错解:A或B或C
错解分析:A、B两项的刻度尺,它们的量程、分度值、类型皆不合适。一般情况下,学校操场的长度为几百米,形状多为类椭圆形,利用A、B两项的刻度尺测量,不仅工作繁重且误差也比较大。C、D两项皆为卷尺,但它们的量程和分度值皆不相同,相较而言,显然D项更加合适。
正解:D
探究题
小芳同学观察到许多建筑材料的截面多是V形或U形,这引起了她的好奇心。
[提出问题]物体能够承受的压力的最大值与哪些因素有关
[猜想与假设]猜想一:物体能够承受的压力的最大值与物体的形状有关。
猜想二:物体能够承受的压力的最大值与物体的材料有关
[设计实验]小芳利用如图所示的装置,选取了纸条、细绳、火柴盒和若干火柴棒,对猜想一进行实验探究。
[进行实验与收集数据](1)选取材料和长、宽、厚相同的纸条若干。
(2)将一张纸条折成V形,放在装置上,在纸条两端距中点(支点)相同距离处,各挂一相同的火柴盒。在两端火柴盒中逐渐增加数量 的火柴棒,直到纸条被压弯折为止,将一端火柴盒中火柴棒的根数记录在下表中。
(3)将纸条分别折成U形、圆弧形,重复步骤(2).
(4)更换纸条,将以上实验再做两次。
[分析与论证]分析实验数据,可以得出的结论是(写出一条即可): .
[交流与合作](1)生产、生活中利用上述结论的事例很多,如巨大的铁桥中多处使用了U形钢材。请你举出一个利用V形或圆弧形结构的实例: 。
(2)若要探究猜想二,实验中应使所选物体的
和 相同。
解:[进行实验与收集数据] (2)相同
[分析与论证]完全相同的纸条,圆弧形纸条能够承受的压力最大(或物体能够承受的压力的最大值与形状有关)
[交流与合作](1)V形的有:厂房的屋架、塔吊支架;圆弧形的有:隧道顶、桥洞、拱形桥等(2)形状;长、宽、厚
同课章节目录
