九年级数学(人教版)上册复习课件-第22章二次函数
文档属性
| 名称 | 九年级数学(人教版)上册复习课件-第22章二次函数 |

|
|
| 格式 | zip | ||
| 文件大小 | 615.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-15 00:00:00 | ||
图片预览











文档简介
课件59张PPT。二次函数复习课二次函数知识点导航:1、二次函数的定义
2、二次函数的图像及性质
3、求解析式的三种方法
4、二次函数与一元二次方程的关系
5、 a,b,c及相关符号的确定
二次函数的一般形式 函数y=ax2+bx+c
其中a、b、c是常数
切记:a≠0
右边一个x的二次多项式(不能是分式或根式)
二次函数的特殊形式:
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2 1、 说出下列二次函数的二次项系数、一次项系
数、常数项(1) y=-x2+58x-112
(2)y=πx22、指出下列函数y=ax2+bx+c中的a、b、c(1) y=-3x2-x-1(3) y=x(1+x)(2) y=5x2-6
一、二次函数的定义3.下列函数中,哪些是二次函数?先化简后判断(5)y=ax2+bx+c
4.当m____时,函数y=(m+1)χ - 2χ+1
是二次函数?知识运用
下列函数中,哪些是二次函数?
(1)y=3x-1 (2)y=3x2
(3)y=3x3+2x2 (4)y=2x2-2x+1
(5)y=x -2 +x (6)y=x2-x(1+x)驶向胜利的彼岸当m取何值时,函数是y= (m+2)x
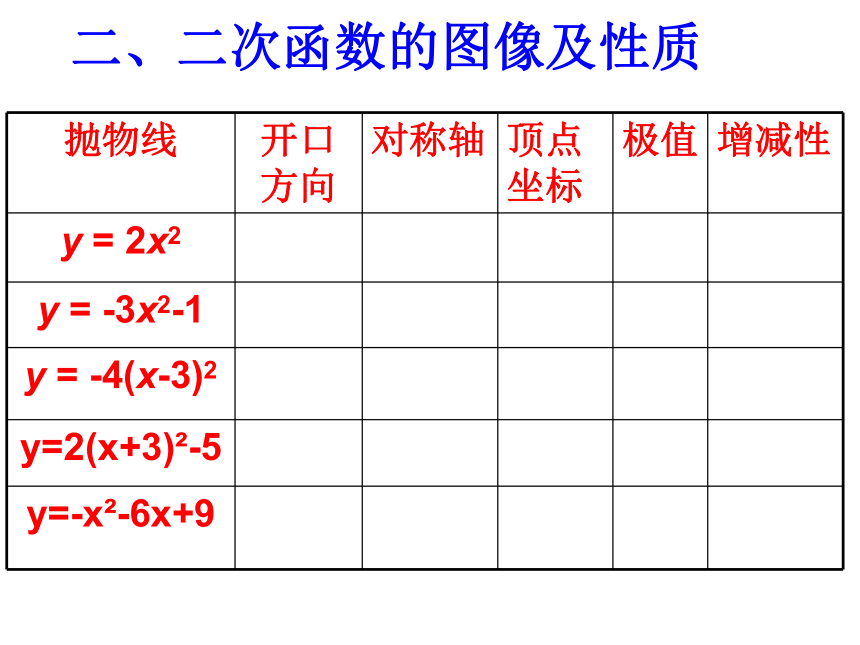
分别 是一次函数? 反比例函数? 知识运用m2-2二次函数?二、二次函数的图像及性质 巩固练习1:
(1)抛物线y = x 2的开口向 ,对称轴是 ,顶点坐标是 ,图象过第 象限 ;(2)已知y = - nx 2 (n>0) , 则图象 ( )
(填“可能”或“不可能”)过点A(-2,3)。上Y轴(0,0)一、二不可能(3)抛物线y = x 2+3的开口向 ,对称轴是 , 顶点坐标是 ,是由抛物线
y = x 2向 平移 个单位得到的;上直线X=0(0,3)上3(2)已知(如图)抛物线y = ax 2+k的图象,则a 0,k 0;若图象过A (0,-2) 和B (2,0) ,则a = ,k = ;函数关系式是y = 。〉〈0.5-20.5x 2-2
5.函数y=(m+1)xm2+m是二次函数,其图像开口向下,则m=____,顶点在____,
当x___时,y随x的增大而增大,
当x___时,y随x的增大而减小。
6.对称轴是直线x=-2的抛物线是( )A.B.C.D.C7.抛物线 的顶点坐标是( )C8. 抛物线 的对称轴 .直线x=n-m9.抛物线的顶点为(3,5) 此抛物线的解析式可设为( )
A.y=a(x+3)2+5 B.y=a(x-3)2+5
C.y=a(x-3)2-5 D.y=a(x+3)2-5
10.抛物线c1的解析式为y=2(x-1)2+3抛物线c2与抛物线c1关于x轴对称,请直接写出抛物线c2的解析式___________。关于y轴对称呢?By=-2(x-1)2-311.一条抛物线与抛物线y=-2(x+2)2的形状相同,顶点坐标为(-1,3),这条抛物线的解析式为__________ 13.在平面直角坐标系中,如果抛物线 不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是 . 12.若二次函数 经过平移变换后顶点坐标为(-2,3) ,则平移后的函数解析式为 .14、填空:
(1)已知函数y=—x2-x-4,当函数值y随
x的增大而减小时,x的取值范围是___________
(2)二次函数y=mx2-3x+2m-m2的图象
经过原点,则m= ____。x<12(四) 形如y = a (x+h) 2 +k (a ≠0) 的二次函数a > 0 a < 0直线X=-h(-h,k)练习巩固2:
(1)抛物线 y = 2 (x –3 ) 2+1 的开口向 , 对称轴 , 顶点坐标是
(2)若抛物线y = a (x+m) 2+n开口向下,顶点在第四象限,则a 0, m 0, n 0。 上X=3(3,1)〈〈〈015.选择
(1)抛物线y=3x2-1的___________
A 开口向上,有最高点 B 开口向上,有最低点
C 开口向下,有最高点 D 开口向下,有最低点
(2)若y=ax2+bx+c(a ? 0)与x轴交于点A(2,0), B(4,0),
则对称轴是______
A 直线x=2 B直线x=4 C 直线x=3 D直线x= -3
(3)若y=ax2+bx+c(a ? 0)的图象过点A(2,m), B(4,m),
则对称轴是______
A 直线x=3 B 直线x=4 C 直线x= -3 D直线x=2
BCA已知三个点坐标三对对应值,选择一般式已知顶点坐标或对称轴或最值,选择顶点式 已知抛物线与x轴的两交点坐标,选择交点式三、求二次函数的解析式
一般式 y=ax2+bx+c (a≠0)
顶点式 y=a(x-h)2+k (a≠0)
交点式 y=a(x-x1)(x-x2) (a≠0)
用待定系数法确定二次函数的解析式时,应该根据条件的特点,恰当地选用一种函数表达式。 根据下列条件,求二次函数的解析式。16、图象经过(0,0), (1,-2) , (2,3) 三点;17、图象的顶点(2,3), 且经过点(3,1) ;18、直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).求抛物线的解析式 。二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
(1)有两个交点
(2)有一个交点
(3)没有交点b2 – 4ac > 0b2 – 4ac= 0b2 – 4ac< 0若抛物线y=ax2+bx+c与x轴有交点,则b2 – 4ac≥0四、二次函数与一元二次方程的关系19.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=____,此时抛物线 y=x2-2x+m与x轴有____个交点.20.已知抛物线 y=x2 – 8x +c的顶点在 x轴上,则c=____.1116 21.一元二次方程 3 x2+x-10=0的两个根是
x1= -2 ,x2=5/3, 那么二次函数y= 3 x2+x-10与x轴的交点坐标是____.
(-2、0)(5/3、0)22、已知二次函数y=ax2-5x+c的图象如图。(1)、当x为何值时,y随x的增大而增大;
(2)、当x为何值时,y<0。(5)、求它的解析式和顶点坐标;(3)、当x为何值时,y=0(4)、当x为何值时,
ax2-5x+c>023、二次函数y=ax2+bx+c(a≠0)的图象如图所示,则a、b、c的符号为( )
A、a<0,b>0,c>0 B、a<0,b>0,c<0
C、a<0,b<0,c>0 D、a<0,b<0,c<0B五、a,b,c及相关符号的确定 24、二次函数y=ax2+bx+c(a≠0)的图象
如图所示,则a、b、c的符号为( )
A、a>0,b>0,c=0 B、a<0,b>0,c=0
C、a<0,b<0,c<0 D、a>0,b<0,c=0Ao25、二次函数y=ax2+bx+c(a≠0)的图象如图
所示,则a、b、c 、 △的符号为( )
A、a>0,b=0,c>0,△>0
B、a<0,b>0,c<0,△=0
C、a>0,b=0,c<0,△>0
D、a<0,b=0,c<0,△<0 Co26.抛物线y=ax2+bx+c(a≠0)的图象经过原点和二、三、四象限,判断a、b、c的符号情况:a 0,b 0,c 0.
<=<27.抛物线y=ax2+bx+c(a≠0)的图象经过原点,且它的顶点在第三象限,则a、b、c满足的条件是:a 0,b 0,c 0. >=>28.二次函数y=ax2+bx+c中,如果a>0,b<0,c<0,那么这个二次函数图象的顶点必在第___ 象限 四29.已知二次函数的图像如图所示,下列结论:
⑴a+b+c=0 ⑵a-b+c﹥0 ⑶abc ﹥0
⑷b=2a 其中正确的结论的个数是( )
A 1个 B 2个 C 3个 D 4个D1x-10y30.在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为
答案: B直击中考1.抛物线y=x2-6x+5 的顶点坐标为( )
A.(3,-4) B.(3,4)
C.(-3,-4) D.(-3,4)
2.抛物线y=-6x2 可以看作是由
抛物线y=-6x2+5按下列何种变换得到( )
A.向上平移5个单位 B.向下平移5个单位
C.向左平移5个单位 D.向右平移5个单位
3.二次函数y=(x-1)2+2的最小值是( )
A.2 B.1 C.-1 D.-2
4.抛物线y=-(x+2)2-3的顶点坐标是( )
A.(2,-3) B.(-2,3)
C.(2,3) D.(-2,-3)
5.抛物线y=a(x+1)(x-3)(a≠0)的对称轴是直线( )
A.x=1 B.x=-1 C.x=-3 D.x=36.二次函数y=-2x2+4x+1的图象如何平移就得到y=-2x2的图象( )
A.向左平移1个单位,再向上平移3个单位
B.向右平移1个单位,再向上平移3个单位
C.向左平移1个单位,再向下平移3个单位
D.向右平移1个单位,再向下平移3个单位
8.二次函数y=ax2+bx+c的图象如图所示,
则下列关系式不正确的是( )
A.a<0
B.abc>0
C.a+b+c>0
D.b2-4ac>0
9由二次函数y=2(x-3)2+1,可知( )
A.其图象的开口向下
B.其图象的对称轴为直线x=-3
C.其最小值为1
D.当x<3时,y随x的增大而增大10.已知函数y=(k-3)x2+2x+1的图象与x轴有交点,则k的取值范围是( )
A.k<4 B.k≤4
C.k<4且k≠3 D.k≤4且k≠3·新课标12.二次函数y=ax2+bx+c的图象如图,反比列函数y=a/x与正比列函数y=bx在同一坐标系内的大致图象是( )·新课标14.抛物线y=x2+bx+c的图象向右平移2个单位,再向下平移3个单位,所得图象的解析式为y=x2-2x-3,则b、c的值为( )
A.b=2,c=2 B.b=2,c=0
C.b=-2,c=-1 D.b=-3,c=215.如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )16.在平面直角坐标系中,将抛物线
y=x2+2x+3 绕着它与y轴的交点旋转180°,所得抛物线的解析式是( )
A.y=-(x+1)2+2 B.y=-(x-1)2+4
C.y=-(x-1)2+2 D.y=-(x+1)2+4
17.已知二次函数的图象(0≤x≤3)如图所示,关于该函数在所给自变量取值范围内,下列说法正确的是( )A.有最小值0,有最大值3
B.有最小值-1,有最大值0
C.有最小值-1,有最大值3
D.有最小值-1,无最大值18.一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式:
h=-5(t-1)2+6,则小球距离地面的最大高度是( )
A.1米 B.5米 C.6米 D.7米
19.若二次函数y=-x2+2x+k的部分图象如图所示,则关于x的一元二次方程-x2+2x+k=0的一个解x1=3,另一个解x2=___.20.点A(2,y1)、B(3,y2)是二次函数y=x2-2x+1的图象上两点,则y1与y2的大小关系为y1________y2(填“>”“<”“=”).21.已知二次函数y=ax2+bx+c(a≠0),其中a、b、c满足a+b+c=0和9a-3b+c=0,则该二次函数图象的对称轴是直线________.归纳知识点:抛物线y=ax2+bx+c的符号问题:(1)a的符号:由抛物线的开口方向确定开口向上a>0开口向下a<0(2)C的符号:由抛物线与y轴的交点位置确定.交点在x轴上方c>0交点在x轴下方c<0经过坐标原点c=0(3)b的符号:由对称轴的位置确定对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0(4)b2-4ac的符号:由抛物线与x轴的交点个数确定与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<017.根据下列表格中二次函数y=ax2+bx+c的自变量与函数值的对应值,判断方程ax2+bx+c =0
(a≠0, a, b, c为常数)的一个解的范围是( )A.6.17< X <6.18 B.6.18< X <6.19
C.-0.01< X <0.02 D.6.19< X <6.20B2、已知抛物线顶点坐标(h, k),通常设抛物线解析式为_______________3、已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________1、已知抛物线上的三点,通常设解析式为________________y=ax2+bx+c(a≠0)y=a(x-h)2+k(a≠0)y=a(x-x1)(x-x2) (a≠0)求抛物线解析式的三种方法练习 根据下列条件,求二次函数的解析式。(1)、图象经过(0,0), (1,-2) , (2,3) 三点;(2)、图象的顶点(2,3), 且经过点(3,1) ;(3)、图象经过(-2,0), (3,0) ,且最高点
的纵坐标是3 。 例1、已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1 ∴顶点坐标为( 1 , 2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a (3-1)2+2 ∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
即: y=-2x2+4x22.已知二次函数y=ax2+bx+c(a≠0)的图像如图所示,根据图像解答下列问题: (1)写出方程ax2+bx+c=0的两个根; (2)写出下列不等式ax2+bx+c>0的解集; (3)写出y随x的增大而减小的自变量x的取值范围; (4)若方程ax2+bx+c=k
有两个不相等的实数根,
求k的取值范围。 23.如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图象上有一点D(x,y)(其中x>0,y>0),使S△ABD=S△ABC,求点D的坐标.在矩形荒地ABCD中,AB=10,BC=6,今在四边上分别选取E、F、G、H四点,且AE=AH=CF=CG=x,建一个花园,如何设计,可使花园面积最大?DCABGHFE106再显身手解:设花园的面积为y
则 y=60-x2 -(10-x)(6-x)=-2x2 + 16x(0
2、二次函数的图像及性质
3、求解析式的三种方法
4、二次函数与一元二次方程的关系
5、 a,b,c及相关符号的确定
二次函数的一般形式 函数y=ax2+bx+c
其中a、b、c是常数
切记:a≠0
右边一个x的二次多项式(不能是分式或根式)
二次函数的特殊形式:
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2 1、 说出下列二次函数的二次项系数、一次项系
数、常数项(1) y=-x2+58x-112
(2)y=πx22、指出下列函数y=ax2+bx+c中的a、b、c(1) y=-3x2-x-1(3) y=x(1+x)(2) y=5x2-6
一、二次函数的定义3.下列函数中,哪些是二次函数?先化简后判断(5)y=ax2+bx+c
4.当m____时,函数y=(m+1)χ - 2χ+1
是二次函数?知识运用
下列函数中,哪些是二次函数?
(1)y=3x-1 (2)y=3x2
(3)y=3x3+2x2 (4)y=2x2-2x+1
(5)y=x -2 +x (6)y=x2-x(1+x)驶向胜利的彼岸当m取何值时,函数是y= (m+2)x
分别 是一次函数? 反比例函数? 知识运用m2-2二次函数?二、二次函数的图像及性质 巩固练习1:
(1)抛物线y = x 2的开口向 ,对称轴是 ,顶点坐标是 ,图象过第 象限 ;(2)已知y = - nx 2 (n>0) , 则图象 ( )
(填“可能”或“不可能”)过点A(-2,3)。上Y轴(0,0)一、二不可能(3)抛物线y = x 2+3的开口向 ,对称轴是 , 顶点坐标是 ,是由抛物线
y = x 2向 平移 个单位得到的;上直线X=0(0,3)上3(2)已知(如图)抛物线y = ax 2+k的图象,则a 0,k 0;若图象过A (0,-2) 和B (2,0) ,则a = ,k = ;函数关系式是y = 。〉〈0.5-20.5x 2-2
5.函数y=(m+1)xm2+m是二次函数,其图像开口向下,则m=____,顶点在____,
当x___时,y随x的增大而增大,
当x___时,y随x的增大而减小。
6.对称轴是直线x=-2的抛物线是( )A.B.C.D.C7.抛物线 的顶点坐标是( )C8. 抛物线 的对称轴 .直线x=n-m9.抛物线的顶点为(3,5) 此抛物线的解析式可设为( )
A.y=a(x+3)2+5 B.y=a(x-3)2+5
C.y=a(x-3)2-5 D.y=a(x+3)2-5
10.抛物线c1的解析式为y=2(x-1)2+3抛物线c2与抛物线c1关于x轴对称,请直接写出抛物线c2的解析式___________。关于y轴对称呢?By=-2(x-1)2-311.一条抛物线与抛物线y=-2(x+2)2的形状相同,顶点坐标为(-1,3),这条抛物线的解析式为__________ 13.在平面直角坐标系中,如果抛物线 不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是 . 12.若二次函数 经过平移变换后顶点坐标为(-2,3) ,则平移后的函数解析式为 .14、填空:
(1)已知函数y=—x2-x-4,当函数值y随
x的增大而减小时,x的取值范围是___________
(2)二次函数y=mx2-3x+2m-m2的图象
经过原点,则m= ____。x<12(四) 形如y = a (x+h) 2 +k (a ≠0) 的二次函数a > 0 a < 0直线X=-h(-h,k)练习巩固2:
(1)抛物线 y = 2 (x –3 ) 2+1 的开口向 , 对称轴 , 顶点坐标是
(2)若抛物线y = a (x+m) 2+n开口向下,顶点在第四象限,则a 0, m 0, n 0。 上X=3(3,1)〈〈〈015.选择
(1)抛物线y=3x2-1的___________
A 开口向上,有最高点 B 开口向上,有最低点
C 开口向下,有最高点 D 开口向下,有最低点
(2)若y=ax2+bx+c(a ? 0)与x轴交于点A(2,0), B(4,0),
则对称轴是______
A 直线x=2 B直线x=4 C 直线x=3 D直线x= -3
(3)若y=ax2+bx+c(a ? 0)的图象过点A(2,m), B(4,m),
则对称轴是______
A 直线x=3 B 直线x=4 C 直线x= -3 D直线x=2
BCA已知三个点坐标三对对应值,选择一般式已知顶点坐标或对称轴或最值,选择顶点式 已知抛物线与x轴的两交点坐标,选择交点式三、求二次函数的解析式
一般式 y=ax2+bx+c (a≠0)
顶点式 y=a(x-h)2+k (a≠0)
交点式 y=a(x-x1)(x-x2) (a≠0)
用待定系数法确定二次函数的解析式时,应该根据条件的特点,恰当地选用一种函数表达式。 根据下列条件,求二次函数的解析式。16、图象经过(0,0), (1,-2) , (2,3) 三点;17、图象的顶点(2,3), 且经过点(3,1) ;18、直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).求抛物线的解析式 。二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
(1)有两个交点
(2)有一个交点
(3)没有交点b2 – 4ac > 0b2 – 4ac= 0b2 – 4ac< 0若抛物线y=ax2+bx+c与x轴有交点,则b2 – 4ac≥0四、二次函数与一元二次方程的关系19.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=____,此时抛物线 y=x2-2x+m与x轴有____个交点.20.已知抛物线 y=x2 – 8x +c的顶点在 x轴上,则c=____.1116 21.一元二次方程 3 x2+x-10=0的两个根是
x1= -2 ,x2=5/3, 那么二次函数y= 3 x2+x-10与x轴的交点坐标是____.
(-2、0)(5/3、0)22、已知二次函数y=ax2-5x+c的图象如图。(1)、当x为何值时,y随x的增大而增大;
(2)、当x为何值时,y<0。(5)、求它的解析式和顶点坐标;(3)、当x为何值时,y=0(4)、当x为何值时,
ax2-5x+c>023、二次函数y=ax2+bx+c(a≠0)的图象如图所示,则a、b、c的符号为( )
A、a<0,b>0,c>0 B、a<0,b>0,c<0
C、a<0,b<0,c>0 D、a<0,b<0,c<0B五、a,b,c及相关符号的确定 24、二次函数y=ax2+bx+c(a≠0)的图象
如图所示,则a、b、c的符号为( )
A、a>0,b>0,c=0 B、a<0,b>0,c=0
C、a<0,b<0,c<0 D、a>0,b<0,c=0Ao25、二次函数y=ax2+bx+c(a≠0)的图象如图
所示,则a、b、c 、 △的符号为( )
A、a>0,b=0,c>0,△>0
B、a<0,b>0,c<0,△=0
C、a>0,b=0,c<0,△>0
D、a<0,b=0,c<0,△<0 Co26.抛物线y=ax2+bx+c(a≠0)的图象经过原点和二、三、四象限,判断a、b、c的符号情况:a 0,b 0,c 0.
<=<27.抛物线y=ax2+bx+c(a≠0)的图象经过原点,且它的顶点在第三象限,则a、b、c满足的条件是:a 0,b 0,c 0. >=>28.二次函数y=ax2+bx+c中,如果a>0,b<0,c<0,那么这个二次函数图象的顶点必在第___ 象限 四29.已知二次函数的图像如图所示,下列结论:
⑴a+b+c=0 ⑵a-b+c﹥0 ⑶abc ﹥0
⑷b=2a 其中正确的结论的个数是( )
A 1个 B 2个 C 3个 D 4个D1x-10y30.在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为
答案: B直击中考1.抛物线y=x2-6x+5 的顶点坐标为( )
A.(3,-4) B.(3,4)
C.(-3,-4) D.(-3,4)
2.抛物线y=-6x2 可以看作是由
抛物线y=-6x2+5按下列何种变换得到( )
A.向上平移5个单位 B.向下平移5个单位
C.向左平移5个单位 D.向右平移5个单位
3.二次函数y=(x-1)2+2的最小值是( )
A.2 B.1 C.-1 D.-2
4.抛物线y=-(x+2)2-3的顶点坐标是( )
A.(2,-3) B.(-2,3)
C.(2,3) D.(-2,-3)
5.抛物线y=a(x+1)(x-3)(a≠0)的对称轴是直线( )
A.x=1 B.x=-1 C.x=-3 D.x=36.二次函数y=-2x2+4x+1的图象如何平移就得到y=-2x2的图象( )
A.向左平移1个单位,再向上平移3个单位
B.向右平移1个单位,再向上平移3个单位
C.向左平移1个单位,再向下平移3个单位
D.向右平移1个单位,再向下平移3个单位
8.二次函数y=ax2+bx+c的图象如图所示,
则下列关系式不正确的是( )
A.a<0
B.abc>0
C.a+b+c>0
D.b2-4ac>0
9由二次函数y=2(x-3)2+1,可知( )
A.其图象的开口向下
B.其图象的对称轴为直线x=-3
C.其最小值为1
D.当x<3时,y随x的增大而增大10.已知函数y=(k-3)x2+2x+1的图象与x轴有交点,则k的取值范围是( )
A.k<4 B.k≤4
C.k<4且k≠3 D.k≤4且k≠3·新课标12.二次函数y=ax2+bx+c的图象如图,反比列函数y=a/x与正比列函数y=bx在同一坐标系内的大致图象是( )·新课标14.抛物线y=x2+bx+c的图象向右平移2个单位,再向下平移3个单位,所得图象的解析式为y=x2-2x-3,则b、c的值为( )
A.b=2,c=2 B.b=2,c=0
C.b=-2,c=-1 D.b=-3,c=215.如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )16.在平面直角坐标系中,将抛物线
y=x2+2x+3 绕着它与y轴的交点旋转180°,所得抛物线的解析式是( )
A.y=-(x+1)2+2 B.y=-(x-1)2+4
C.y=-(x-1)2+2 D.y=-(x+1)2+4
17.已知二次函数的图象(0≤x≤3)如图所示,关于该函数在所给自变量取值范围内,下列说法正确的是( )A.有最小值0,有最大值3
B.有最小值-1,有最大值0
C.有最小值-1,有最大值3
D.有最小值-1,无最大值18.一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式:
h=-5(t-1)2+6,则小球距离地面的最大高度是( )
A.1米 B.5米 C.6米 D.7米
19.若二次函数y=-x2+2x+k的部分图象如图所示,则关于x的一元二次方程-x2+2x+k=0的一个解x1=3,另一个解x2=___.20.点A(2,y1)、B(3,y2)是二次函数y=x2-2x+1的图象上两点,则y1与y2的大小关系为y1________y2(填“>”“<”“=”).21.已知二次函数y=ax2+bx+c(a≠0),其中a、b、c满足a+b+c=0和9a-3b+c=0,则该二次函数图象的对称轴是直线________.归纳知识点:抛物线y=ax2+bx+c的符号问题:(1)a的符号:由抛物线的开口方向确定开口向上a>0开口向下a<0(2)C的符号:由抛物线与y轴的交点位置确定.交点在x轴上方c>0交点在x轴下方c<0经过坐标原点c=0(3)b的符号:由对称轴的位置确定对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0(4)b2-4ac的符号:由抛物线与x轴的交点个数确定与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<017.根据下列表格中二次函数y=ax2+bx+c的自变量与函数值的对应值,判断方程ax2+bx+c =0
(a≠0, a, b, c为常数)的一个解的范围是( )A.6.17< X <6.18 B.6.18< X <6.19
C.-0.01< X <0.02 D.6.19< X <6.20B2、已知抛物线顶点坐标(h, k),通常设抛物线解析式为_______________3、已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________1、已知抛物线上的三点,通常设解析式为________________y=ax2+bx+c(a≠0)y=a(x-h)2+k(a≠0)y=a(x-x1)(x-x2) (a≠0)求抛物线解析式的三种方法练习 根据下列条件,求二次函数的解析式。(1)、图象经过(0,0), (1,-2) , (2,3) 三点;(2)、图象的顶点(2,3), 且经过点(3,1) ;(3)、图象经过(-2,0), (3,0) ,且最高点
的纵坐标是3 。 例1、已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1 ∴顶点坐标为( 1 , 2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a (3-1)2+2 ∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
即: y=-2x2+4x22.已知二次函数y=ax2+bx+c(a≠0)的图像如图所示,根据图像解答下列问题: (1)写出方程ax2+bx+c=0的两个根; (2)写出下列不等式ax2+bx+c>0的解集; (3)写出y随x的增大而减小的自变量x的取值范围; (4)若方程ax2+bx+c=k
有两个不相等的实数根,
求k的取值范围。 23.如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图象上有一点D(x,y)(其中x>0,y>0),使S△ABD=S△ABC,求点D的坐标.在矩形荒地ABCD中,AB=10,BC=6,今在四边上分别选取E、F、G、H四点,且AE=AH=CF=CG=x,建一个花园,如何设计,可使花园面积最大?DCABGHFE106再显身手解:设花园的面积为y
则 y=60-x2 -(10-x)(6-x)=-2x2 + 16x(0
同课章节目录
