8.2.2一元一次不等式 课件

课件20张PPT。 8.2一元一次不等式（2）
——一元一次不等式的解法教学过程 不等式的性质什么？一元一次方程的定义？
含______未知数，等号左右
两边都是______，并且未知
数的次数都是____的方程，
叫做一元一次方程.1232X+3=11是什么方程？性质1：不等式的两边同时加上（或减去）同一个整式，不等号的方向不变.
性质2 ：不等式的两边乘（或除以）同一个正数，不等号的方向不变.
性质 3：不等式的两边乘（或除以）同一个负数，不等号的方向改变。
注意： 必须把不等号的方向改变
整式一个一次1． 引入一元一次不等式概念共同特点：
①只含______未知数 ②不等号左右两边都是_____
③并且未知数最高次数都是____。 含一个未知数，不等号左右两边都是整式，并且未知数的次数是一次的不等式，叫做一元一次不等式.
一个整式一次复习回顾一元一次不等式定义：????????合作交流 在前面我们学习过解方程，回忆一下解一元一次方程的过程，它的每一步的依据是什么？一、有分母的去分母：方程两边同时乘以公分母，
依据是等式的基本性质2;二、有括号的去括号：依据是去括号法则；三、移项合并同类项：移项的依据是 等式的基本性质1； 四、把未知数的系数化成1：依据是等式的基本性质2。合作交流@探索新知@解方程
（1）2X+3=11解不等式
2X+3>11解：移项，得
2X=11-3
合并同类项，得
2X=8
系数化为1，得
X=4 求不等式解集的过程叫解不等式。
合并同类项，得
2X>8
系数化为1，得
X>4
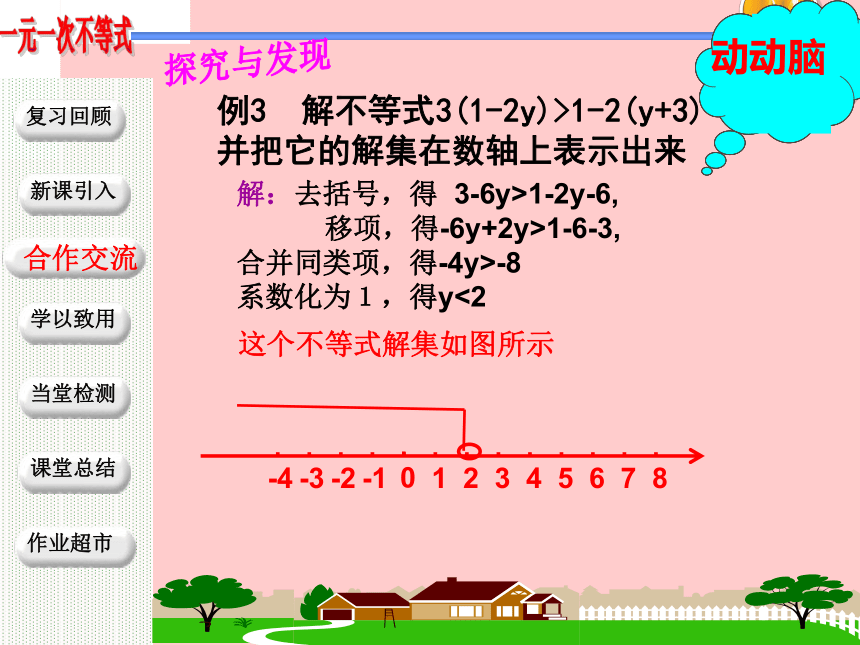
合作交流动动脑探究与发现例3 解不等式3(1-2y)>1-2(y+3)并把它的解集在数轴上表示出来解：去括号，得 3-6y>1-2y-6,
　　　移项，得-6y+2y>1-6-3,
合并同类项，得-4y>-8
系数化为１，得y<2这个不等式解集如图所示合作交流 例4 解下列不等式，并把它的解集在数轴上表示出来解：
去分母，不等式两边同乘-6，不等号方向改变，
得 3(X-3) ≤ 2(2X-1)-6
去括号，得 3X-9 ≤ 4X-2-6
移项，得 3X-4X ≤ 9-2-6
合并同类项，得 -X ≤ 1
系数化为1，得 X ≥ - 1 此不等式解集如图所示≥（1）去分母
（2）去括号
（3）移项
（4）合并同类项
（5）系数化为1（1）去分母
（2）去括号
（3）移项
（4）合并同类项
（5）系数化为1在（1）与（5）这两步若乘数（或除数）为负数，要把不等号方向改变两边同时除以未知数的系数思考： 解一元一次不等式的过程和解一元一次方程的过程有什么联系？
合作交流1.解不等式3(1-x) ≤2(x+9)，并把解集表示在数轴上2.（重庆·中考）解不等式 并把解集在数轴上表示出来． 解集：X≥-3解集：X<2课堂小测，选择你喜欢的水果当堂检测，选择你喜欢的水果当堂检测，选择你喜欢的水果若ax＜1的解集是x＞ ，则a一定是（ ）
A.非负数 B.非正数 C.负数 D.正数当堂检测，选择你喜欢的水果下列是一元一次不等式的是（ ）
A. B.x2>9 C.2x+y≤5 D..当堂检测，选择你喜欢的水果不等式1＋x＜0的解集在数轴上表示正确的是（ ）
A B C D当堂检测，选择你喜欢的水果不等式1＋x＜0的解集在数轴上表示正确的是（ ）
A B C D下列是一元一次不等式的是（ ）
A. B.x2>9 C.2x+y≤5 D..
A.非负数 B.非正数 C.负数 D.正数若ax＜1的解集是x＞ ，则a一定是（ ）解一元一次不等式的步骤是什么？我的收获 通过本节课的学习，你有哪些收获？不妨和大家分享交流一下。1、必做题：P95页中习题8.2的第3题（1）（3）
2、选做题：P95页中习题8.2的第6、8、9、10题；THANK YOU! ^_^GOOD LUCK!