人教版 八年级下学期一次函数图像的性质与平移课件
文档属性
| 名称 | 人教版 八年级下学期一次函数图像的性质与平移课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-15 00:00:00 | ||
图片预览



文档简介
课件22张PPT。-6o-4246246-2-2-4xy一次函数的图像天才=1%的灵感+99%的汗水马投涧镇一中一.复习:
1.作函数图像的步骤是什么?(1)列表 (2)描点 (3)连线2. 一次函数图像的特点是什么?
一次函数y=kx+b (k≠0)的图象是一条直线,切经过点(0,b)
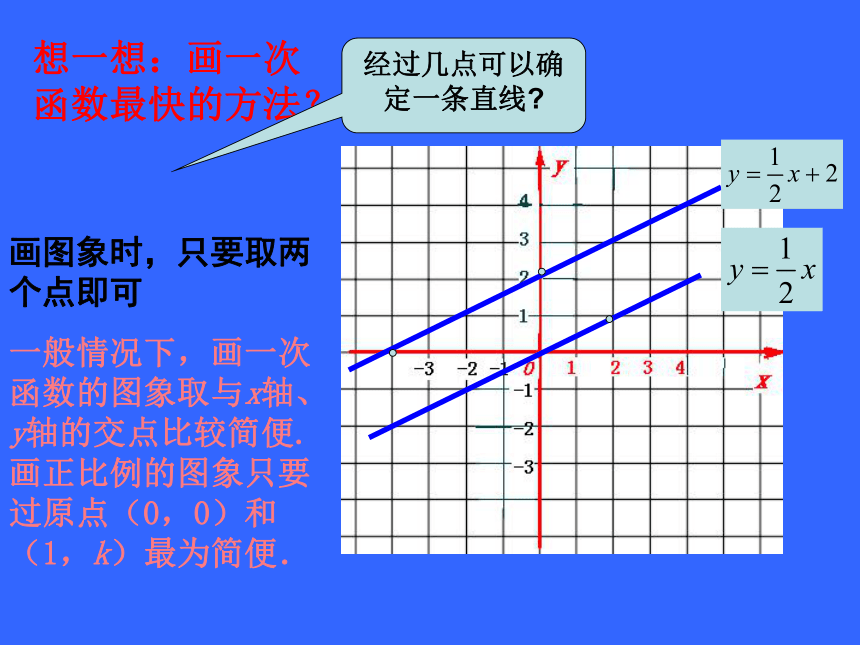
这条直线通常又称为直线y=kx+b(k≠0) 画图象时,只要取两个点即可
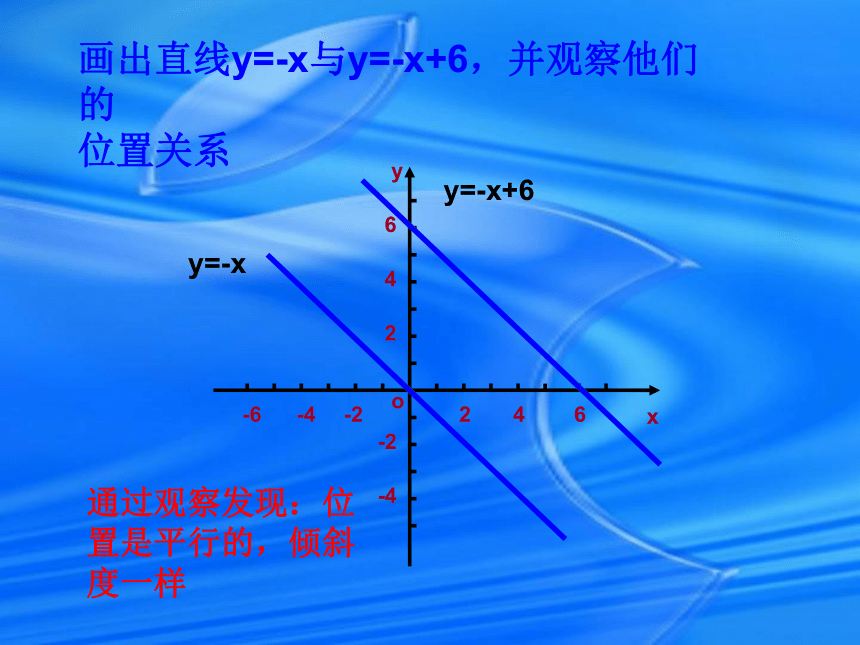
一般情况下,画一次函数的图象取与x轴、y轴的交点比较简便.画正比例的图象只要过原点(0,0)和(1,k)最为简便.想一想:画一次函数最快的方法?经过几点可以确定一条直线?画出直线y=-x与y=-x+6,并观察他们的
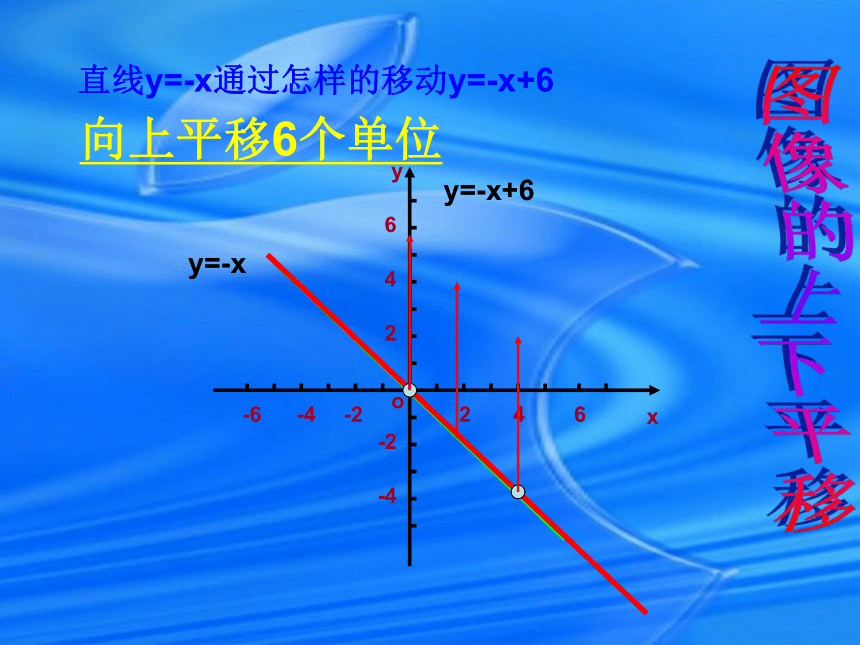
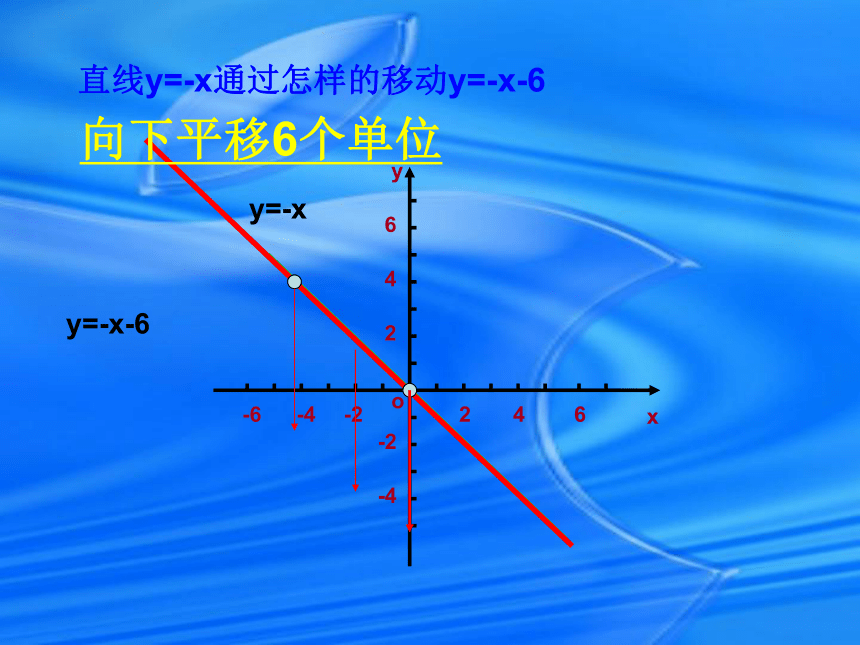
位置关系-6o-446246-2-2-4xy2y=-x+6y=-x通过观察发现:位置是平行的,倾斜度一样直线y=-x通过怎样的移动y=-x+6-6o-446246-2-2-4xy2y=-x+6y=-x向上平移6个单位图像的上下平移直线y=-x通过怎样的移动y=-x-6-6o-446246-2-2-4xy2y=-x-6y=-x向下平移6个单位六.探索发现(1) 在同一坐标系中作出下列函数的图象
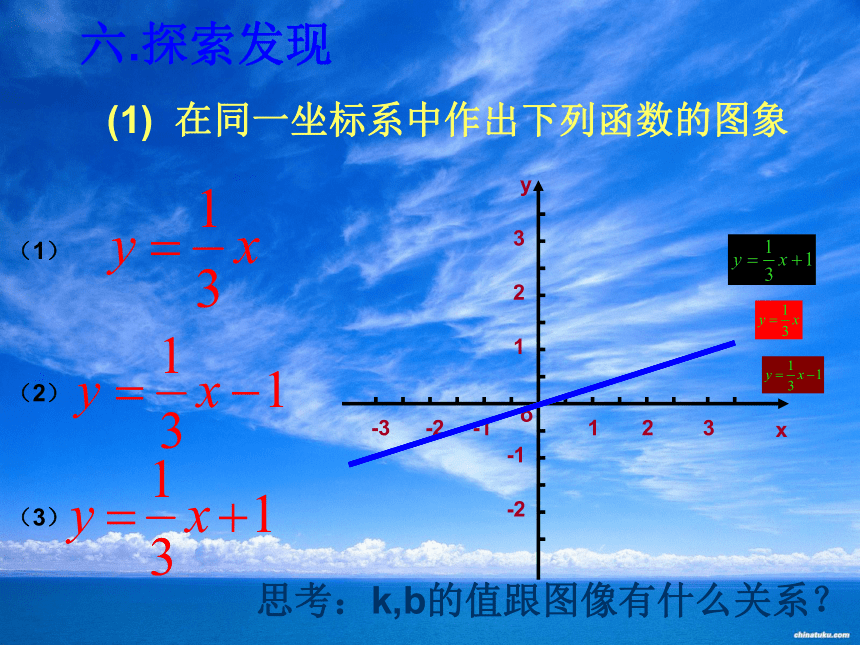
(1)(2)(3)-3o-223123-1-1-2xy1思考:k,b的值跟图像有什么关系?结论:
(1)一次函数y=kx+b的图像可以看做是y=kx平移|b|个单位长度而得到(b>0时,向上平移,b<0时,向下平移。)
(2)图像的上下平移与K无关
(3)图像的上下平移与b有关,图像向上移动b的值增加,图像向下移动b的值减小。
简称:上 + 下 –
(1)图像的左右平移与k,b无关,只与自变量x有关系,向左移动x的值增加,向右移动x的值减小。
简称:左 + 右 -
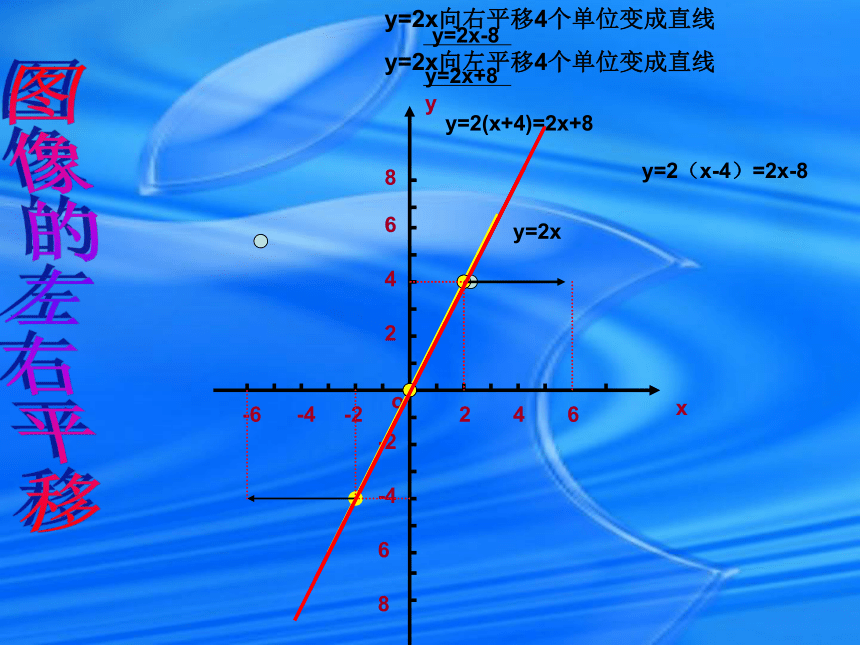
-6o-446246-2-2-4xy2y=2x向右平移4个单位变成直线
y=2x向左平移4个单位变成直线 868y=2xy=2(x+4)=2x+8y=2(x-4)=2x-8y=2x-8y=2x+8图像的左右平移-(2)在同一坐标系中作出下列函数的图象(1)(2)(3)-3o-223123-1-1-2xy1做了这三个图像你发现了
K,b跟图像的关系吗?思考结论
(1)图像的左右平移与k,b无关,只与自变量x有关系,向左移动x的值增加,向右移动x的值减小。
简称:左 + 右 -画出一次函数 的图象 31y30X观察分析: 当一个点在直线上从左向右移动时,它的位置怎样变化 自变量x由___到___函数y的值从___到___大小小大画出一次函数 的图象 31y30X观察分析: 自变量x由___到___函数y的值从___到___大小小大函数y=3x-2的图象是否也有这种现象 y随x的增大而增大,
这时函数的图象从左到右上升; 结论的图象 观察分析: 自变量x由___到___函数y的值从___到___大小小大y随x的增大而减小,
这时函数的图象从左到右下降; 结论一次函数y=kx+b有下列性质:
?
(1) 当k>0时,y随x的增大而_____ ,这时函数的图象从左到右_____ ;
?
(2) 当k<0时,y随x的增大而_____,这时函数的图象从左到右_____. 概括减小下降增大上升五.想一想 1)x从0开始逐渐增
大时,y=2x+6和y=5x
哪一个的值先达到20?
这说明了什么?-15o-10101551015-5-5-10x205yy=5x
y=2x+6
你看出来了吗?结论K>ob=0b>0b<0b=0b>0b<0通过作以上一次函数的图像我们发现y=kx+b
中,k,b的取值跟图像的关系如下:K<0一,三一,二,三一,三,四二,四一,二,四二,三,四当k>0时,y的值随x的增大而增大当k<0时,y的值随x的增大而减小(3)七.练一练1.下列一次函数中,y的值随x的增大
而减小的有________。(3)(4)(2) (4)(1) y=10x-9(2) y=-0.3x+22.下列哪个图像是一次函数y=-3x+5
和y=2x-4的大致图像( )(A)(B)(C)(D)B历史使人聪明,诗歌使人机智,数学使人精细。3.如果一次函数y=kx-3k+6的图象经
过原点,那么k的值为_________。4.写出m的3个值,使相应的一次函数
y = (2m-1)x+2的值都是随x的增大而减小.K=2可以写无数个,只要满足2m-1<0就可以了。例如:m=0.m=-1,m=-2八.小结:本节课的主要内容有:1.一次函数及其图像的性质有哪些?2.函数图像的平移有着怎样的规律?3.一次函数图像的变化趋势及经过的象限?再见付出定有回报,努力就有收获。
同学们扬起你们理想的风帆,带上你们的智慧,
迈向明天------
明天会更好
1.作函数图像的步骤是什么?(1)列表 (2)描点 (3)连线2. 一次函数图像的特点是什么?
一次函数y=kx+b (k≠0)的图象是一条直线,切经过点(0,b)
这条直线通常又称为直线y=kx+b(k≠0) 画图象时,只要取两个点即可
一般情况下,画一次函数的图象取与x轴、y轴的交点比较简便.画正比例的图象只要过原点(0,0)和(1,k)最为简便.想一想:画一次函数最快的方法?经过几点可以确定一条直线?画出直线y=-x与y=-x+6,并观察他们的
位置关系-6o-446246-2-2-4xy2y=-x+6y=-x通过观察发现:位置是平行的,倾斜度一样直线y=-x通过怎样的移动y=-x+6-6o-446246-2-2-4xy2y=-x+6y=-x向上平移6个单位图像的上下平移直线y=-x通过怎样的移动y=-x-6-6o-446246-2-2-4xy2y=-x-6y=-x向下平移6个单位六.探索发现(1) 在同一坐标系中作出下列函数的图象
(1)(2)(3)-3o-223123-1-1-2xy1思考:k,b的值跟图像有什么关系?结论:
(1)一次函数y=kx+b的图像可以看做是y=kx平移|b|个单位长度而得到(b>0时,向上平移,b<0时,向下平移。)
(2)图像的上下平移与K无关
(3)图像的上下平移与b有关,图像向上移动b的值增加,图像向下移动b的值减小。
简称:上 + 下 –
(1)图像的左右平移与k,b无关,只与自变量x有关系,向左移动x的值增加,向右移动x的值减小。
简称:左 + 右 -
-6o-446246-2-2-4xy2y=2x向右平移4个单位变成直线
y=2x向左平移4个单位变成直线 868y=2xy=2(x+4)=2x+8y=2(x-4)=2x-8y=2x-8y=2x+8图像的左右平移-(2)在同一坐标系中作出下列函数的图象(1)(2)(3)-3o-223123-1-1-2xy1做了这三个图像你发现了
K,b跟图像的关系吗?思考结论
(1)图像的左右平移与k,b无关,只与自变量x有关系,向左移动x的值增加,向右移动x的值减小。
简称:左 + 右 -画出一次函数 的图象 31y30X观察分析: 当一个点在直线上从左向右移动时,它的位置怎样变化 自变量x由___到___函数y的值从___到___大小小大画出一次函数 的图象 31y30X观察分析: 自变量x由___到___函数y的值从___到___大小小大函数y=3x-2的图象是否也有这种现象 y随x的增大而增大,
这时函数的图象从左到右上升; 结论的图象 观察分析: 自变量x由___到___函数y的值从___到___大小小大y随x的增大而减小,
这时函数的图象从左到右下降; 结论一次函数y=kx+b有下列性质:
?
(1) 当k>0时,y随x的增大而_____ ,这时函数的图象从左到右_____ ;
?
(2) 当k<0时,y随x的增大而_____,这时函数的图象从左到右_____. 概括减小下降增大上升五.想一想 1)x从0开始逐渐增
大时,y=2x+6和y=5x
哪一个的值先达到20?
这说明了什么?-15o-10101551015-5-5-10x205yy=5x
y=2x+6
你看出来了吗?结论K>ob=0b>0b<0b=0b>0b<0通过作以上一次函数的图像我们发现y=kx+b
中,k,b的取值跟图像的关系如下:K<0一,三一,二,三一,三,四二,四一,二,四二,三,四当k>0时,y的值随x的增大而增大当k<0时,y的值随x的增大而减小(3)七.练一练1.下列一次函数中,y的值随x的增大
而减小的有________。(3)(4)(2) (4)(1) y=10x-9(2) y=-0.3x+22.下列哪个图像是一次函数y=-3x+5
和y=2x-4的大致图像( )(A)(B)(C)(D)B历史使人聪明,诗歌使人机智,数学使人精细。3.如果一次函数y=kx-3k+6的图象经
过原点,那么k的值为_________。4.写出m的3个值,使相应的一次函数
y = (2m-1)x+2的值都是随x的增大而减小.K=2可以写无数个,只要满足2m-1<0就可以了。例如:m=0.m=-1,m=-2八.小结:本节课的主要内容有:1.一次函数及其图像的性质有哪些?2.函数图像的平移有着怎样的规律?3.一次函数图像的变化趋势及经过的象限?再见付出定有回报,努力就有收获。
同学们扬起你们理想的风帆,带上你们的智慧,
迈向明天------
明天会更好
