人教版高中物理必修一4.7 牛顿第二定律应用 专题五、六 瞬时问题、动态问题 课件 (共28张PPT)
文档属性
| 名称 | 人教版高中物理必修一4.7 牛顿第二定律应用 专题五、六 瞬时问题、动态问题 课件 (共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 343.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-10-15 22:21:05 | ||
图片预览








文档简介
课件28张PPT。牛顿第二定律应用之 五-瞬时问题专题【例1】如图(a)所示,一质量为m的物体系于长度分别为L1、L2的两根细绳上,L1的一端悬挂在天花板上,与竖直方向夹角为θ,L2水平拉直,物体处于平衡状态,现将L2线剪断,求剪断瞬间物体的加速度。(2)若将图a中的细线L1改为长度相同、质量不计的轻弹簧,如图b所示,其他条件不变,现将L2线剪断,求剪断瞬间物体的加速度。a=gsinθ a=gtanθ 专题五、瞬时性问题 (1)物体运动的加速度a与其所受的合外力F有瞬时对应关系,
每一瞬时的加速度只取决于这一瞬时的合外力,而与这一瞬时之前或之后的力无关,不等于零的合外力作用的物体上,物体立即产生加速度;若合外力的大小或方向改变,加速度的大小或方向也立即(同时)改变;若合外力变为零,加速度也立即变为零(物体运动的加速度可以突变)。二、突变类问题(力的瞬时性) (2)中学物理中的“绳”和“线”,是理想化模型,具有如下几个特性:
A.轻:即绳(或线)的质量和重力均可视为等于零,同一根绳(或线)的两端及其中间各点的张为大小相等。
B.软:即绳(或线)只能受拉力,不能承受压力(因绳能变曲),绳与其物体相互间作用力的方向总是沿着绳子且朝绳收缩的方向。
C.不可伸长:即无论绳所受拉力多大,绳子的长度不变,即绳子中的张力可以突变。 (3)中学物理中的“弹簧”和“橡皮绳”,也是理想化模型,具有如下几个特性:
A.轻:即弹簧(或橡皮绳)的质量和重力均可视为等于零,同一弹簧的两端及其中间各点的弹力大小相等。
B.弹簧既能承受拉力,也能承受压力(沿着弹簧的轴线),橡皮绳只能承受拉力。不能承受压力。
C、由于弹簧和橡皮绳受力时,要发生形变需要一段时间,所以弹簧和橡皮绳中的弹力不能发生突变。 二、突变类问题(力的瞬时性) 例二:如图3-2-8所示是两根轻弹簧与两个质量都为m的小球连接成的系统,上面一根弹簧的上端固定在天花板上,两小球之间还连接了一根不可伸长的细线.该系统静止,细线受到的拉力大小等于4mg.在剪断了两球之间的细线的瞬间,球A的加速度aA和球B的加速度aB分别是 ( )
A.2g,竖直向下;2g,竖直向下
B.4g,竖直向上;4g,竖直向下
C.2g,竖直向上;2g,竖直向下
D.2g,竖直向下;4g,竖直向下B练习.如图所示,竖直光滑杆上套有一个小球和两个弹簧,两弹簧的一端各与小球相连,另一端用销钉M、N固定于杆上,小球处于静止状态,设拨去销钉M瞬间,小球加速度a的大小为12m/s2,若不拨去销钉M而拨去销钉N瞬间,小球的加速度可能是:
A.22m/s2,竖直向上
B.22m/s2,竖直向下
C.2m/s2,竖直向上
D.2m/s2,竖直向下( BC)练习2、如图所示,小球质量为m,被三根质量不计的弹簧A、B、C拉住,弹簧间的夹角均为1200,小球平衡时, A、B、C的弹力大小之比为3:3:1,当剪断C瞬间,小球的加速度大小及方向可能为
①g/2,竖直向下;②g/2,竖直向上;
③g/4,竖直向下;④g/4,竖直向上;
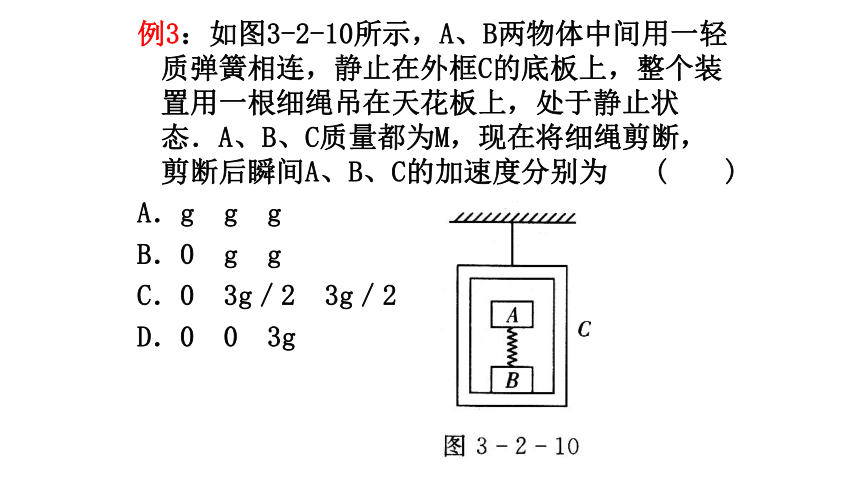
A、①②;B、①④;C、②③;D、③④;答案C. 例3:如图3-2-10所示,A、B两物体中间用一轻质弹簧相连,静止在外框C的底板上,整个装置用一根细绳吊在天花板上,处于静止状态.A、B、C质量都为M,现在将细绳剪断,剪断后瞬间A、B、C的加速度分别为 ( )
A.g g g
B.0 g g
C.0 3g/2 3g/2
D.0 0 3g雨滴从高空由静止落下,若雨滴下落时空气对其的阻力随雨滴下落的速度增大而增大, 试正确做出反映雨滴下落运动速度随时间变化情况的图象牛顿第二定律专题六——动态分析专题13典例探究例1 如图所示,物体在水平拉力F的作用下沿水平地面做匀速直线运动,速度为v.现让拉力F逐渐减小,则物体的加速度和速度的变化情况应是( )
A.加速度逐渐变小,速度逐渐变大
B.加速度和速度都在逐渐变小
C.加速度和速度都在逐渐变大
D.加速度逐渐变大,速度逐渐变小答案:D14变式1静止在光滑水平面上的物体,在水平推力F作用下开始运动,推力随时间变化的规律如图4-3-7所示,关于物体在0~t1时间内的运动情况,正确的描述是( )
A.物体先做匀加速运动,后做匀减速运动
B.物体的速度一直增大
C.物体的速度先增大后减小
D.物体的加速度一直增大答案:B15变式2 如图所示,光滑的水平面上,有一木块以速度v向右运动,一根弹簧固定在墙上,木块从与弹簧接触直到弹簧被压缩到最短的这一段时间内,木块将做什么运动( )
A.匀减速运动
B.速度减小,加速度减小
C.速度减小,加速度增大
D.速度增大,加速度增大答案:C16例2 如图4-3-2所示,自由下落的小球,从它接触竖直放置的弹簧开始,到弹簧压缩到最大限度的过程中,小球的速度和加速度的变化情况是( )
A.加速度变大,速度变小
B.加速度变小,速度变大
C.加速度先变小后变大,
速度先变大后变小
D.加速度先变小后变大,
速度先变小后变大答案:C17变式2 在光滑水平面上有一物块受一水平恒定推力F推的作用而运动,在其正前方固定一个足够长的轻质弹簧,如图所示,当物块与弹簧接触后,下列说法正确的是( )
A.物块接触弹簧后即做减速运动
B.物块接触弹簧后先加速后减速
C.当弹簧处于最大压缩量时,物块的加速度不等于零
D.当物块的速度为零时,
它所受的合力为零答案:BC18
加速度、速度关系的动态分析动态分析问题是牛顿第二定律的典型应用问题之一,可用动力学知识解决问题。
解题思路:
应注意的问题:
(1)物体所受合力的方向决定a的方向。
(2)合力与V同向,物体加速,反之减速。
(3)物体的运动情况取决于物体受的力和物体的初始条件确定受力情况(变力与恒力)确定a确定物体运动19小结小结动态分析的解题步骤:
(1)受力分析,确定变力与恒力,合力方向;
(2)判断合力与v方向的关系:同向,加速;反向,减速。
(3)求出a,分析a的大小变化及方向。
注意:分析过程的转折点,分段分析。2010/29/2018 2:06 PM新郑二中分校高一物理备课组21例一: (2010·广东外国语学校模拟)在动摩擦因数μ=0.2的水平面上有一个质量为m=1 kg的小球,小球与水平轻弹簧及与竖直方向成θ=45°角的不可伸长的轻绳一端相连,如图3-2-2所示.此时小球处于静止平衡状态,且水平面对小球的弹力恰好为零,当剪断轻绳的瞬间,取g=10 m/s2.求:
(1)此时轻弹簧的弹力大小;
(2)小球的加速度大小和方向;[思路点拨] 解答本题时应注意以下两点:
(1)当其他力变化时,弹簧的弹力不能在瞬间发生变化;
(2)当其他力变化时,细绳上的拉力可以在瞬间发生变化.[课堂笔记] (1)水平面对小球的弹力为零,小球在绳没有断时受到绳的拉力FT、重力mg和弹簧的弹力FN作用而处于平衡状态,依据平衡条件得
竖直方向有:FTcosθ=mg,
水平方向有:FTsinθ=FN,
解得弹簧的弹力为:FN=mgtanθ=10 N(2)剪断绳后小球在竖直方向仍平衡,水平面支持力与重力平衡FN′=mg,
由牛顿第二定律得小球的加速度为:
a= =8 m/s2,方向向左.[答案] (1)10 N (2)8 m/s2 方向向左 练习如图5所示,质量为m的小球用水平轻弹簧系住,并用倾角为30°的光滑木板AB托住,小球恰好处于静止状态.当木板AB突然向下撤离的瞬间,小球的加速度大小为多少?例六:如图所示,在倾角为=300的光滑斜面上,有两个用轻弹簧连接的木块A和B,已知A的质量为2kg,B的质量为3kg,有一恒力F=50N的力作用在A上,在AB具有相同加速度的瞬间,撤去外力F,则这一瞬时,A和B的加速度分别是多大?(g=10m/s2) 例四.如图所示,A、B两小球分别连在弹簧两端,B端用细线固定在倾角为30°的光滑斜面上,若不计弹簧质量,在线被剪断瞬间,A、B两球的加速度分别为
A.都等于 B. 和0
C. 和0 D.0和 D例五:如图,质量相同的物块A、B、C用两个轻弹簧和一根轻线相连,挂在天花板上处于平衡状态。现将A、B之间的轻绳剪断,在刚剪断的瞬间,三个物块的加速度分别是多大?方向如何?
ABC
每一瞬时的加速度只取决于这一瞬时的合外力,而与这一瞬时之前或之后的力无关,不等于零的合外力作用的物体上,物体立即产生加速度;若合外力的大小或方向改变,加速度的大小或方向也立即(同时)改变;若合外力变为零,加速度也立即变为零(物体运动的加速度可以突变)。二、突变类问题(力的瞬时性) (2)中学物理中的“绳”和“线”,是理想化模型,具有如下几个特性:
A.轻:即绳(或线)的质量和重力均可视为等于零,同一根绳(或线)的两端及其中间各点的张为大小相等。
B.软:即绳(或线)只能受拉力,不能承受压力(因绳能变曲),绳与其物体相互间作用力的方向总是沿着绳子且朝绳收缩的方向。
C.不可伸长:即无论绳所受拉力多大,绳子的长度不变,即绳子中的张力可以突变。 (3)中学物理中的“弹簧”和“橡皮绳”,也是理想化模型,具有如下几个特性:
A.轻:即弹簧(或橡皮绳)的质量和重力均可视为等于零,同一弹簧的两端及其中间各点的弹力大小相等。
B.弹簧既能承受拉力,也能承受压力(沿着弹簧的轴线),橡皮绳只能承受拉力。不能承受压力。
C、由于弹簧和橡皮绳受力时,要发生形变需要一段时间,所以弹簧和橡皮绳中的弹力不能发生突变。 二、突变类问题(力的瞬时性) 例二:如图3-2-8所示是两根轻弹簧与两个质量都为m的小球连接成的系统,上面一根弹簧的上端固定在天花板上,两小球之间还连接了一根不可伸长的细线.该系统静止,细线受到的拉力大小等于4mg.在剪断了两球之间的细线的瞬间,球A的加速度aA和球B的加速度aB分别是 ( )
A.2g,竖直向下;2g,竖直向下
B.4g,竖直向上;4g,竖直向下
C.2g,竖直向上;2g,竖直向下
D.2g,竖直向下;4g,竖直向下B练习.如图所示,竖直光滑杆上套有一个小球和两个弹簧,两弹簧的一端各与小球相连,另一端用销钉M、N固定于杆上,小球处于静止状态,设拨去销钉M瞬间,小球加速度a的大小为12m/s2,若不拨去销钉M而拨去销钉N瞬间,小球的加速度可能是:
A.22m/s2,竖直向上
B.22m/s2,竖直向下
C.2m/s2,竖直向上
D.2m/s2,竖直向下( BC)练习2、如图所示,小球质量为m,被三根质量不计的弹簧A、B、C拉住,弹簧间的夹角均为1200,小球平衡时, A、B、C的弹力大小之比为3:3:1,当剪断C瞬间,小球的加速度大小及方向可能为
①g/2,竖直向下;②g/2,竖直向上;
③g/4,竖直向下;④g/4,竖直向上;
A、①②;B、①④;C、②③;D、③④;答案C. 例3:如图3-2-10所示,A、B两物体中间用一轻质弹簧相连,静止在外框C的底板上,整个装置用一根细绳吊在天花板上,处于静止状态.A、B、C质量都为M,现在将细绳剪断,剪断后瞬间A、B、C的加速度分别为 ( )
A.g g g
B.0 g g
C.0 3g/2 3g/2
D.0 0 3g雨滴从高空由静止落下,若雨滴下落时空气对其的阻力随雨滴下落的速度增大而增大, 试正确做出反映雨滴下落运动速度随时间变化情况的图象牛顿第二定律专题六——动态分析专题13典例探究例1 如图所示,物体在水平拉力F的作用下沿水平地面做匀速直线运动,速度为v.现让拉力F逐渐减小,则物体的加速度和速度的变化情况应是( )
A.加速度逐渐变小,速度逐渐变大
B.加速度和速度都在逐渐变小
C.加速度和速度都在逐渐变大
D.加速度逐渐变大,速度逐渐变小答案:D14变式1静止在光滑水平面上的物体,在水平推力F作用下开始运动,推力随时间变化的规律如图4-3-7所示,关于物体在0~t1时间内的运动情况,正确的描述是( )
A.物体先做匀加速运动,后做匀减速运动
B.物体的速度一直增大
C.物体的速度先增大后减小
D.物体的加速度一直增大答案:B15变式2 如图所示,光滑的水平面上,有一木块以速度v向右运动,一根弹簧固定在墙上,木块从与弹簧接触直到弹簧被压缩到最短的这一段时间内,木块将做什么运动( )
A.匀减速运动
B.速度减小,加速度减小
C.速度减小,加速度增大
D.速度增大,加速度增大答案:C16例2 如图4-3-2所示,自由下落的小球,从它接触竖直放置的弹簧开始,到弹簧压缩到最大限度的过程中,小球的速度和加速度的变化情况是( )
A.加速度变大,速度变小
B.加速度变小,速度变大
C.加速度先变小后变大,
速度先变大后变小
D.加速度先变小后变大,
速度先变小后变大答案:C17变式2 在光滑水平面上有一物块受一水平恒定推力F推的作用而运动,在其正前方固定一个足够长的轻质弹簧,如图所示,当物块与弹簧接触后,下列说法正确的是( )
A.物块接触弹簧后即做减速运动
B.物块接触弹簧后先加速后减速
C.当弹簧处于最大压缩量时,物块的加速度不等于零
D.当物块的速度为零时,
它所受的合力为零答案:BC18
加速度、速度关系的动态分析动态分析问题是牛顿第二定律的典型应用问题之一,可用动力学知识解决问题。
解题思路:
应注意的问题:
(1)物体所受合力的方向决定a的方向。
(2)合力与V同向,物体加速,反之减速。
(3)物体的运动情况取决于物体受的力和物体的初始条件确定受力情况(变力与恒力)确定a确定物体运动19小结小结动态分析的解题步骤:
(1)受力分析,确定变力与恒力,合力方向;
(2)判断合力与v方向的关系:同向,加速;反向,减速。
(3)求出a,分析a的大小变化及方向。
注意:分析过程的转折点,分段分析。2010/29/2018 2:06 PM新郑二中分校高一物理备课组21例一: (2010·广东外国语学校模拟)在动摩擦因数μ=0.2的水平面上有一个质量为m=1 kg的小球,小球与水平轻弹簧及与竖直方向成θ=45°角的不可伸长的轻绳一端相连,如图3-2-2所示.此时小球处于静止平衡状态,且水平面对小球的弹力恰好为零,当剪断轻绳的瞬间,取g=10 m/s2.求:
(1)此时轻弹簧的弹力大小;
(2)小球的加速度大小和方向;[思路点拨] 解答本题时应注意以下两点:
(1)当其他力变化时,弹簧的弹力不能在瞬间发生变化;
(2)当其他力变化时,细绳上的拉力可以在瞬间发生变化.[课堂笔记] (1)水平面对小球的弹力为零,小球在绳没有断时受到绳的拉力FT、重力mg和弹簧的弹力FN作用而处于平衡状态,依据平衡条件得
竖直方向有:FTcosθ=mg,
水平方向有:FTsinθ=FN,
解得弹簧的弹力为:FN=mgtanθ=10 N(2)剪断绳后小球在竖直方向仍平衡,水平面支持力与重力平衡FN′=mg,
由牛顿第二定律得小球的加速度为:
a= =8 m/s2,方向向左.[答案] (1)10 N (2)8 m/s2 方向向左 练习如图5所示,质量为m的小球用水平轻弹簧系住,并用倾角为30°的光滑木板AB托住,小球恰好处于静止状态.当木板AB突然向下撤离的瞬间,小球的加速度大小为多少?例六:如图所示,在倾角为=300的光滑斜面上,有两个用轻弹簧连接的木块A和B,已知A的质量为2kg,B的质量为3kg,有一恒力F=50N的力作用在A上,在AB具有相同加速度的瞬间,撤去外力F,则这一瞬时,A和B的加速度分别是多大?(g=10m/s2) 例四.如图所示,A、B两小球分别连在弹簧两端,B端用细线固定在倾角为30°的光滑斜面上,若不计弹簧质量,在线被剪断瞬间,A、B两球的加速度分别为
A.都等于 B. 和0
C. 和0 D.0和 D例五:如图,质量相同的物块A、B、C用两个轻弹簧和一根轻线相连,挂在天花板上处于平衡状态。现将A、B之间的轻绳剪断,在刚剪断的瞬间,三个物块的加速度分别是多大?方向如何?
ABC
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
