人教版八年级上册第十五章数学课件:15.1分式(共28张PPT)
文档属性
| 名称 | 人教版八年级上册第十五章数学课件:15.1分式(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 332.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-15 18:08:19 | ||
图片预览




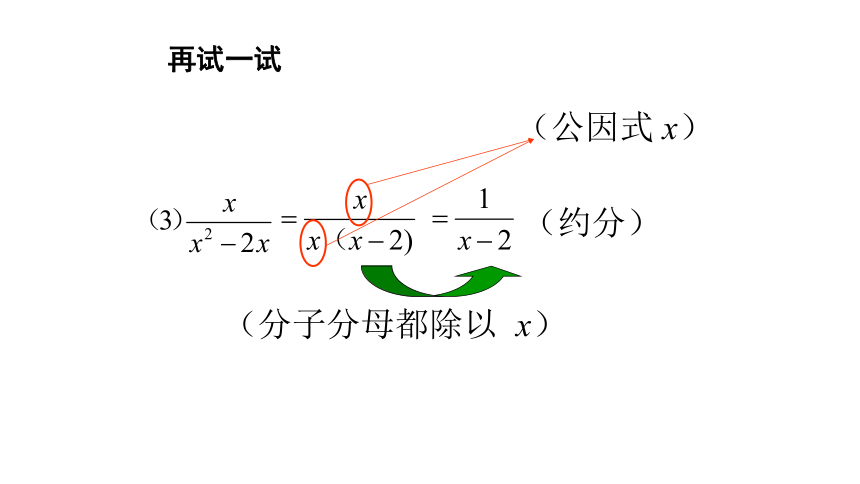




文档简介
课件28张PPT。分式的约分和通分1.分式的基本性质:
分式的分子与分母同乘(或除以)一个 分式的值___________,(C≠0) 2.分式的符号法则:不变复习回顾:用字母表示为:不为0的整式问题情景:2.观察下列式子与第1题的异同,试一试计算:1.约分:观察式子的异同,并计算:再试一试归纳小结: 把一个分式的分子和分母的公因式约去,不改变分式的值,这种变形叫做分式的约分.概念2——最简分式 分子和分母没有公因式的分式称为最简分式..问题:如何找分子分母的公因式?(1)系数:最大公约数(2)字母:相同字母取最低次幂分子分母的公因式:深入探究:问题:如何找分子分母的公因式?先分解因式,再找公因式(3)多项式:找分子分母的公因式的方法:(1)系数:最大公约数(2)字母:相同字母取最低次幂先分解因式,再找公因式(3)多项式: 在约分 时,小颖和小明出现了分歧.小颖:小明:你认为谁的化简对?为什么?√ 分式的约分,通常要使结果成为最简分式或者整式.(分子和分母没有公因式的分式称为最简分式)例:解:
(1)原式=例1 约分(课本 P6)约分的基本步骤:(1)找出分式的分子、分母的公因式(2)原式=(2)约去公因式,化为最简分式因式分解例题设计:如果分式的分子或分母是多项式,先分解因式再约分解:
(3)原式例1 约分(课本 P6)(4)原式变式(注意符号问题)1. 约分:课堂练习:2. 约分3、化简求值:其中其中4.化简求值:,其中 1. 通分:最简公分母:4×3×2=24问题情景:问题 : 类比分数的通分你能把下列分式化为分母相同的分式吗?例题分析:例、通分:最小
公倍数最简
公分母最高
次幂单独字母最简
公分母不同的因式最简
公分母(三)例题分析例1.(课本P7)通分:解:最简公分母是解:最简公分母是通分:最简公分母一般取各分母的所有因式的最高次幂的积作公分母,它叫做最简公分母。3. 三个分式 的最简公分母 是 1.三个分式的最简公分母是( ) B. C. D.2.分式的最简公分母是_________. A.课堂练习:(2)(1)(2)(1)4.通分:5.(补充)通分:例2、通分补充例题: 把一个分式的分子和分母的公因式约去,不改变分式的值,这种变形叫做分式的约分。1.约分的依据是:分式的基本性质2.约分的基本方法是: 先找出分式的分子、分母公因式,再约去公因式.3.约分的结果是:整式或最简分式课时小结;4、把各分式化成相同分母的分式叫做
分式的通分.5、一般取各分母的所有因式的最高次幂
的积作公分母,它叫做最简公分母。
分式的分子与分母同乘(或除以)一个 分式的值___________,(C≠0) 2.分式的符号法则:不变复习回顾:用字母表示为:不为0的整式问题情景:2.观察下列式子与第1题的异同,试一试计算:1.约分:观察式子的异同,并计算:再试一试归纳小结: 把一个分式的分子和分母的公因式约去,不改变分式的值,这种变形叫做分式的约分.概念2——最简分式 分子和分母没有公因式的分式称为最简分式..问题:如何找分子分母的公因式?(1)系数:最大公约数(2)字母:相同字母取最低次幂分子分母的公因式:深入探究:问题:如何找分子分母的公因式?先分解因式,再找公因式(3)多项式:找分子分母的公因式的方法:(1)系数:最大公约数(2)字母:相同字母取最低次幂先分解因式,再找公因式(3)多项式: 在约分 时,小颖和小明出现了分歧.小颖:小明:你认为谁的化简对?为什么?√ 分式的约分,通常要使结果成为最简分式或者整式.(分子和分母没有公因式的分式称为最简分式)例:解:
(1)原式=例1 约分(课本 P6)约分的基本步骤:(1)找出分式的分子、分母的公因式(2)原式=(2)约去公因式,化为最简分式因式分解例题设计:如果分式的分子或分母是多项式,先分解因式再约分解:
(3)原式例1 约分(课本 P6)(4)原式变式(注意符号问题)1. 约分:课堂练习:2. 约分3、化简求值:其中其中4.化简求值:,其中 1. 通分:最简公分母:4×3×2=24问题情景:问题 : 类比分数的通分你能把下列分式化为分母相同的分式吗?例题分析:例、通分:最小
公倍数最简
公分母最高
次幂单独字母最简
公分母不同的因式最简
公分母(三)例题分析例1.(课本P7)通分:解:最简公分母是解:最简公分母是通分:最简公分母一般取各分母的所有因式的最高次幂的积作公分母,它叫做最简公分母。3. 三个分式 的最简公分母 是 1.三个分式的最简公分母是( ) B. C. D.2.分式的最简公分母是_________. A.课堂练习:(2)(1)(2)(1)4.通分:5.(补充)通分:例2、通分补充例题: 把一个分式的分子和分母的公因式约去,不改变分式的值,这种变形叫做分式的约分。1.约分的依据是:分式的基本性质2.约分的基本方法是: 先找出分式的分子、分母公因式,再约去公因式.3.约分的结果是:整式或最简分式课时小结;4、把各分式化成相同分母的分式叫做
分式的通分.5、一般取各分母的所有因式的最高次幂
的积作公分母,它叫做最简公分母。
