人教版八年级上册数学课件 11.2.2 三角形的外角(共34张PPT)
文档属性
| 名称 | 人教版八年级上册数学课件 11.2.2 三角形的外角(共34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 809.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-15 18:11:58 | ||
图片预览




文档简介
课件34张PPT。§11.2.2
三角形的外角火石山中学 刘贵才
2016年5月15日三角形的外角某建筑系的学生站在C处想检测∠A与∠B的和是否符合设计要求,携带测角工具进行测量,但是∠A太高无法测量, ∠B靠近水面也无法测量,你能帮助他求出∠A+∠B吗?一:创境导入,
示标提高。教学目标:
1、了解三角形的外角概念和三角形外角的性质,初步学会数学说理.
2 、会运用简单的说理来计算三角形相关的角.
教学重点:
三角形的外角及其性质.
教学难点:
运用三角形外角性质进行有关计算时能准确地表达推理的过程和方法.
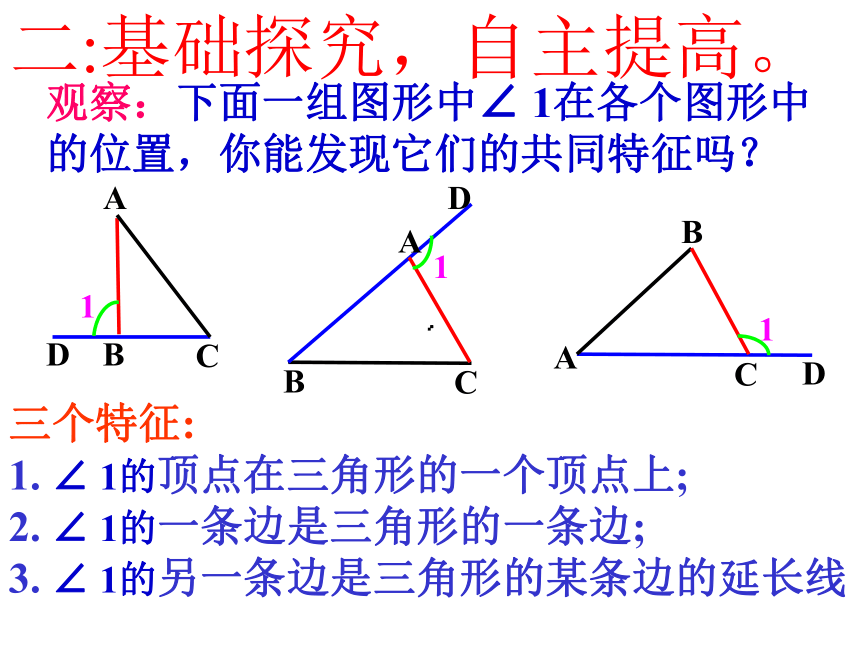
观察:下面一组图形中∠ 1在各个图形中的位置,你能发现它们的共同特征吗?
三个特征:
1. ∠ 1的顶点在三角形的一个顶点上;
2. ∠ 1的一条边是三角形的一条边;
3. ∠ 1的另一条边是三角形的某条边的延长线
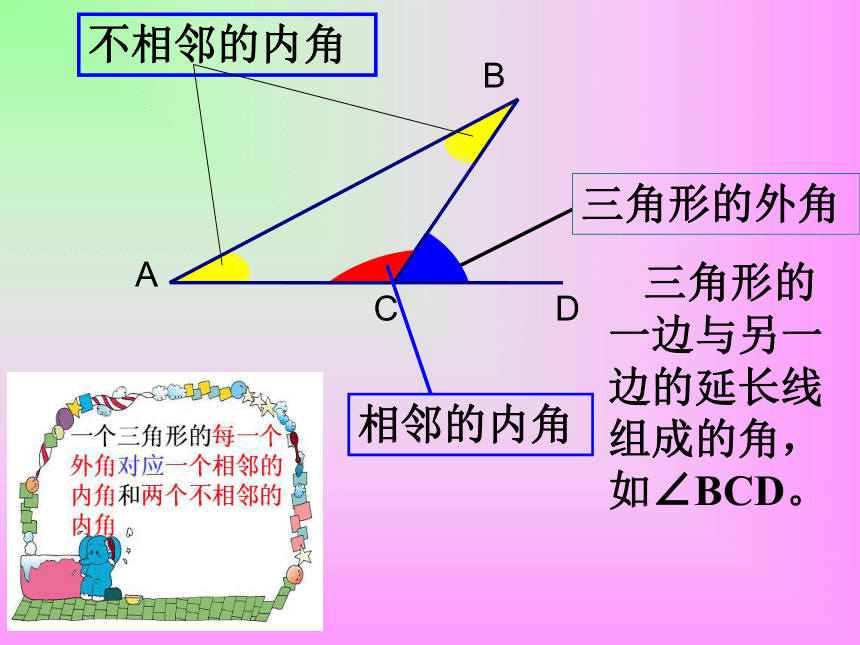
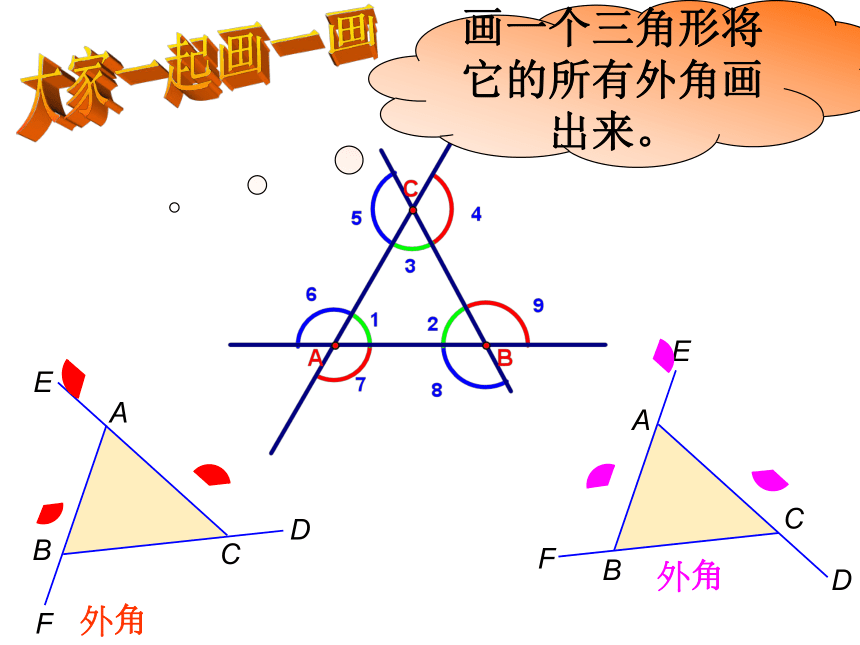
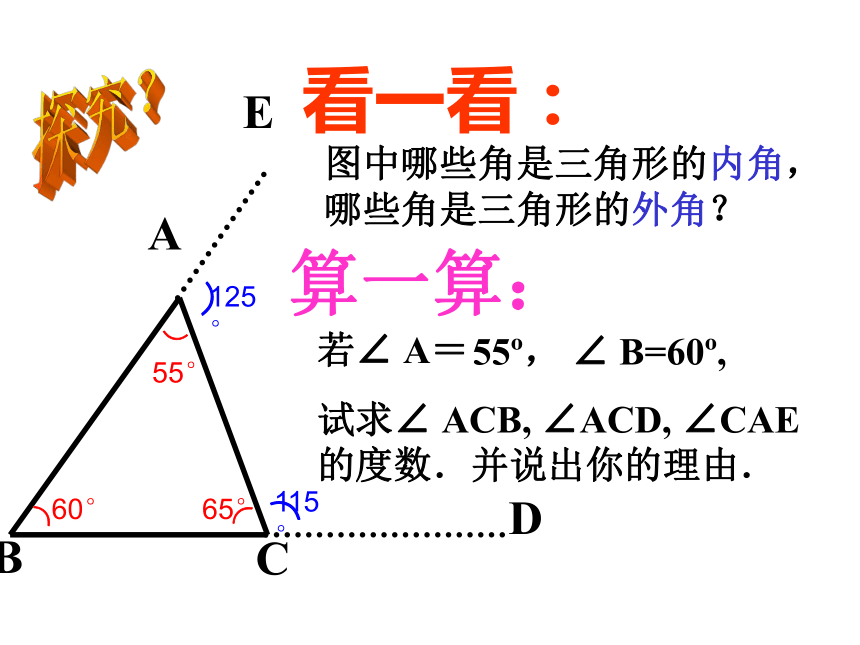
···二:基础探究,自主提高。 三角形的一边与另一边的延长线组成的角,如∠BCD。 大家一起画一画画一个三角形将它的所有外角画出来。ABCDE看一看:算一算:探究?图中哪些角是三角形的内角,
哪些角是三角形的外角?
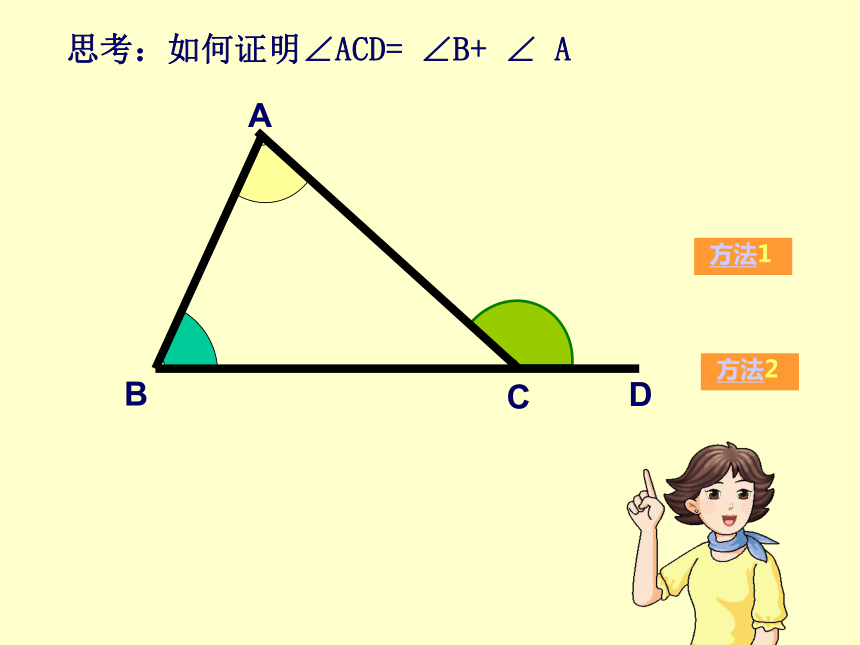
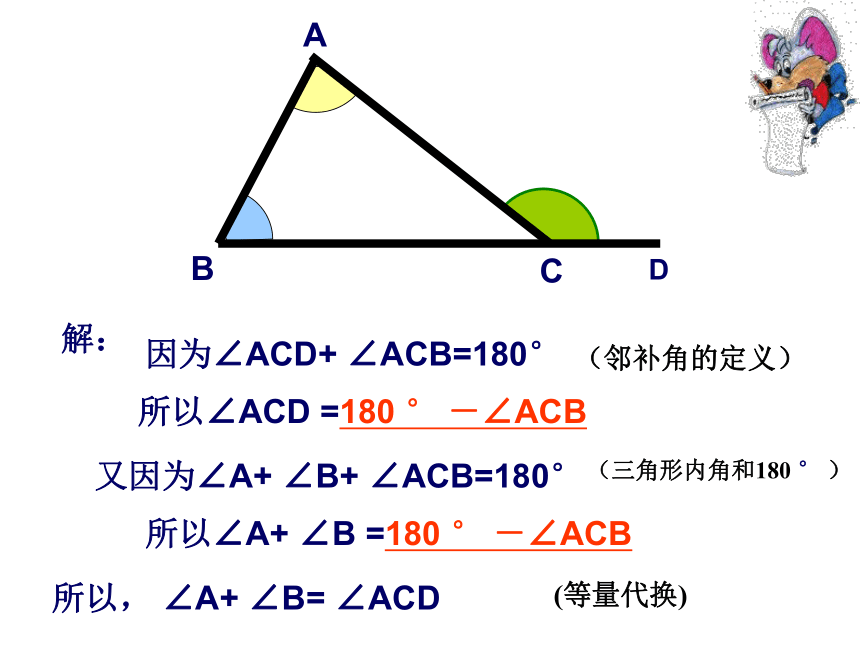
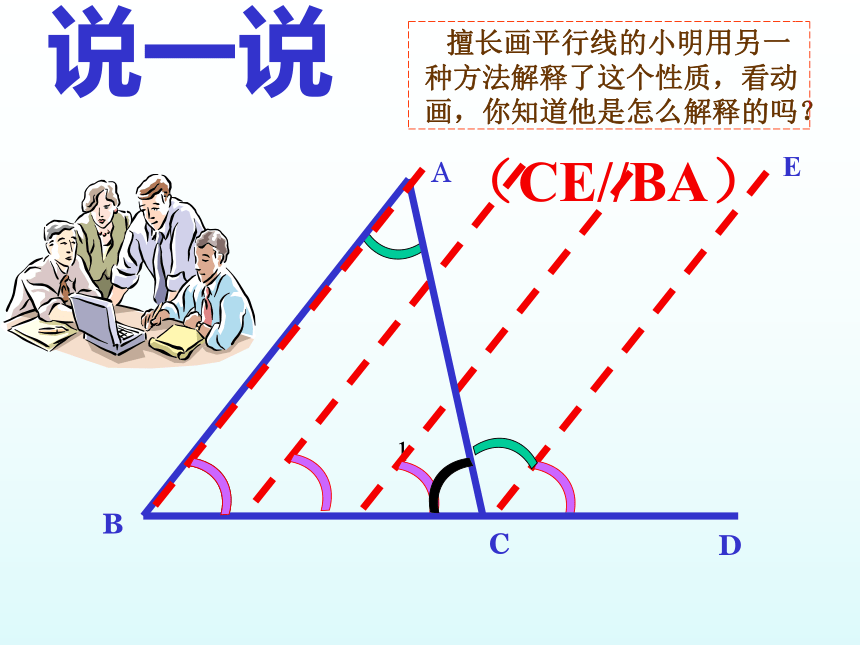
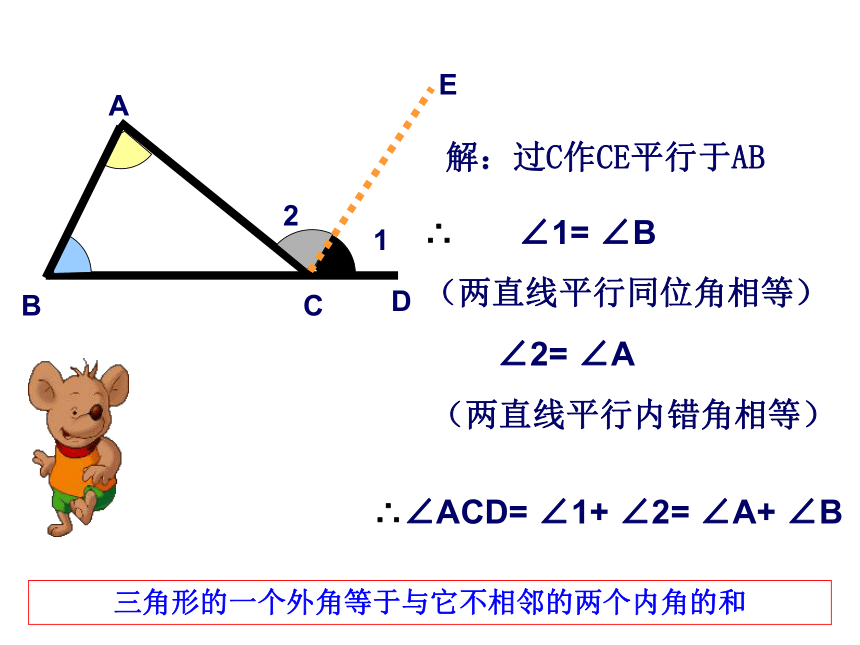
⌒⌒⌒⌒⌒115°60°65°55°125°思考:如何证明∠ACD= ∠B+ ∠ ADD因为∠ACD+ ∠ACB=180°又因为∠A+ ∠B+ ∠ACB=180°所以, ∠A+ ∠B= ∠ACD 解:所以∠ACD =180 ° -∠ACB所以∠A+ ∠B =180 ° -∠ACB(邻补角的定义)(三角形内角和180 ° )(等量代换)1(CE//BA)AE说一说 擅长画平行线的小明用另一种方法解释了这个性质,看动画,你知道他是怎么解释的吗?CBDD解:过C作CE平行于ABABC∴ ∠1= ∠B
(两直线平行同位角相等) ∠2= ∠A
(两直线平行内错角相等)∴∠ACD= ∠1+ ∠2= ∠A+ ∠B三角形的一个外角等于与它不相邻的两个内角的和85o95o60o43o30o求下列各图中∠α的度数。试一试 ∠ACD ∠A (<、>);∠ACD ∠B (<、>)结论:三角形的一个外角大于任何一个与它不相邻的内角。D>>∠ACD= ∠A+ ∠B2、把图中∠1、 ∠2、 ∠3按由大到小的顺序排列∠1∠2∠3>>试一试>>______+______ ______+______ ________快速抢答
看谁答的
又快又准归纳:三角形外角的性质:
1、三角形的一个外角等于
与它不相邻的两个内角的
和。 ∠B+∠C=∠CAD 2、三角形的一个外角大于任何
一个与它不相邻的内角。
∠CAD > ∠B, ∠CAD > ∠C3.三角形的外角和等于360°议一议∠2+ ∠ABC=180°∠3+ ∠ACB=180°三个式子相加得到∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°而∠BAC+ ∠ABC+∠ACB=180°∠1+ ∠2+ ∠3=360°1.你能再借助内外角关系说明
“三角形的外角和等于360°” 2.你能再借助平行线说明
“三角形的外角和等于360°” 吗? D还有别的方法能说明这个结论吗?解:过A作AD∥BC∴ ∠3= ∠4
(两直线平行,同位角相等)BC123A ∠2= ∠BAD
(两直线平行,同旁内角互补)
∴ ∠1+ ∠2+ ∠3= ∠1+ ∠BAD+ ∠4=360°基本思想:转化
让 我 们 一 起 去 发 现CBOACBOA 例题2:一个零件的形状如图所示,按规定∠BAC=90°, ∠B=21°, ∠C=20°,检验工人量得∠BDC=130°,就断定这个零件不合格,你能运用所学的知识说出其中的道理吗?提示:可以先计算出合格时∠BDC的度数,但是∠BDC与∠A 、∠B、 ∠C不在同一个三角形内,因而无法找到它们之间的数量关系,因此需要添加辅助线。那如何添加辅助线才能建立这几个角之间的联系呢?变一变220°已知△ABC中,∠1=50°,
∠2=40 °,∠4=20 °,
则∠3=_______. 国旗上的数学 求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数12FG解:∵∠1是△FBE的外角∴∠1=∠B+ ∠E同理∠2=∠A+∠D在△CFG中
∠C+∠1+∠2=180o∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180oABCDE12F4BACPNMDEF挑战一下!∠A+∠B+∠C+∠D+∠E+∠F=____。360°2、这堂课你记忆最深刻的是什么?1、这堂课你最感兴趣的是什么?小结:3、今天你学会了什么?
三角形的外角火石山中学 刘贵才
2016年5月15日三角形的外角某建筑系的学生站在C处想检测∠A与∠B的和是否符合设计要求,携带测角工具进行测量,但是∠A太高无法测量, ∠B靠近水面也无法测量,你能帮助他求出∠A+∠B吗?一:创境导入,
示标提高。教学目标:
1、了解三角形的外角概念和三角形外角的性质,初步学会数学说理.
2 、会运用简单的说理来计算三角形相关的角.
教学重点:
三角形的外角及其性质.
教学难点:
运用三角形外角性质进行有关计算时能准确地表达推理的过程和方法.
观察:下面一组图形中∠ 1在各个图形中的位置,你能发现它们的共同特征吗?
三个特征:
1. ∠ 1的顶点在三角形的一个顶点上;
2. ∠ 1的一条边是三角形的一条边;
3. ∠ 1的另一条边是三角形的某条边的延长线
···二:基础探究,自主提高。 三角形的一边与另一边的延长线组成的角,如∠BCD。 大家一起画一画画一个三角形将它的所有外角画出来。ABCDE看一看:算一算:探究?图中哪些角是三角形的内角,
哪些角是三角形的外角?
⌒⌒⌒⌒⌒115°60°65°55°125°思考:如何证明∠ACD= ∠B+ ∠ ADD因为∠ACD+ ∠ACB=180°又因为∠A+ ∠B+ ∠ACB=180°所以, ∠A+ ∠B= ∠ACD 解:所以∠ACD =180 ° -∠ACB所以∠A+ ∠B =180 ° -∠ACB(邻补角的定义)(三角形内角和180 ° )(等量代换)1(CE//BA)AE说一说 擅长画平行线的小明用另一种方法解释了这个性质,看动画,你知道他是怎么解释的吗?CBDD解:过C作CE平行于ABABC∴ ∠1= ∠B
(两直线平行同位角相等) ∠2= ∠A
(两直线平行内错角相等)∴∠ACD= ∠1+ ∠2= ∠A+ ∠B三角形的一个外角等于与它不相邻的两个内角的和85o95o60o43o30o求下列各图中∠α的度数。试一试 ∠ACD ∠A (<、>);∠ACD ∠B (<、>)结论:三角形的一个外角大于任何一个与它不相邻的内角。D>>∠ACD= ∠A+ ∠B2、把图中∠1、 ∠2、 ∠3按由大到小的顺序排列∠1∠2∠3>>试一试>>______+______ ______+______ ________快速抢答
看谁答的
又快又准归纳:三角形外角的性质:
1、三角形的一个外角等于
与它不相邻的两个内角的
和。 ∠B+∠C=∠CAD 2、三角形的一个外角大于任何
一个与它不相邻的内角。
∠CAD > ∠B, ∠CAD > ∠C3.三角形的外角和等于360°议一议∠2+ ∠ABC=180°∠3+ ∠ACB=180°三个式子相加得到∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°而∠BAC+ ∠ABC+∠ACB=180°∠1+ ∠2+ ∠3=360°1.你能再借助内外角关系说明
“三角形的外角和等于360°” 2.你能再借助平行线说明
“三角形的外角和等于360°” 吗? D还有别的方法能说明这个结论吗?解:过A作AD∥BC∴ ∠3= ∠4
(两直线平行,同位角相等)BC123A ∠2= ∠BAD
(两直线平行,同旁内角互补)
∴ ∠1+ ∠2+ ∠3= ∠1+ ∠BAD+ ∠4=360°基本思想:转化
让 我 们 一 起 去 发 现CBOACBOA 例题2:一个零件的形状如图所示,按规定∠BAC=90°, ∠B=21°, ∠C=20°,检验工人量得∠BDC=130°,就断定这个零件不合格,你能运用所学的知识说出其中的道理吗?提示:可以先计算出合格时∠BDC的度数,但是∠BDC与∠A 、∠B、 ∠C不在同一个三角形内,因而无法找到它们之间的数量关系,因此需要添加辅助线。那如何添加辅助线才能建立这几个角之间的联系呢?变一变220°已知△ABC中,∠1=50°,
∠2=40 °,∠4=20 °,
则∠3=_______. 国旗上的数学 求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数12FG解:∵∠1是△FBE的外角∴∠1=∠B+ ∠E同理∠2=∠A+∠D在△CFG中
∠C+∠1+∠2=180o∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180oABCDE12F4BACPNMDEF挑战一下!∠A+∠B+∠C+∠D+∠E+∠F=____。360°2、这堂课你记忆最深刻的是什么?1、这堂课你最感兴趣的是什么?小结:3、今天你学会了什么?
