人教版八年级数学下册第十八章平行四边形小结复习课件(共22张PPT)
文档属性
| 名称 | 人教版八年级数学下册第十八章平行四边形小结复习课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-15 00:00:00 | ||
图片预览



文档简介
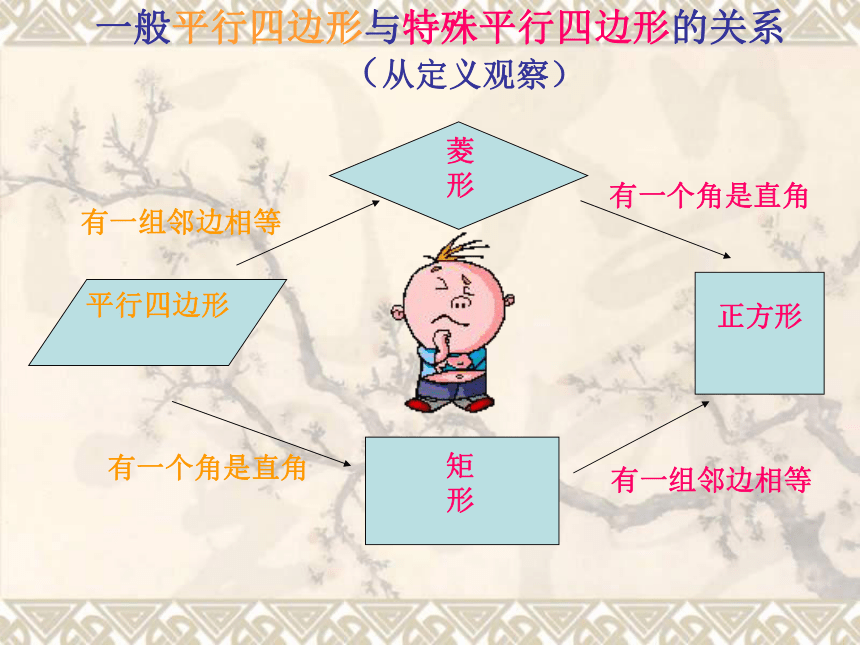
课件22张PPT。 上饶县第七中学 郑 军人教2013版 第十八章 平行四边形 平行四边形小结人民教育出版社2015年4月22日一般平行四边形与特殊平行四边形的关系
(从定义观察)
正方形
矩形菱形平行四边形
有一个角是直角有一组邻边相等有一组邻边相等有一个角是直角几种平行四边形的特征比较 对边平行且相等对边平行且相等对边平行,
四条边都相等对边平行,
四条边相等对角相等,
邻角互补四个角都为直角对角相等,
邻角互补四个角都为直角对角线互相平分对角线相等
且互相平分对角线互相垂直平分,
每条对角线平分对角对角线互相垂直
平分且相等,
每条对角线平分对角
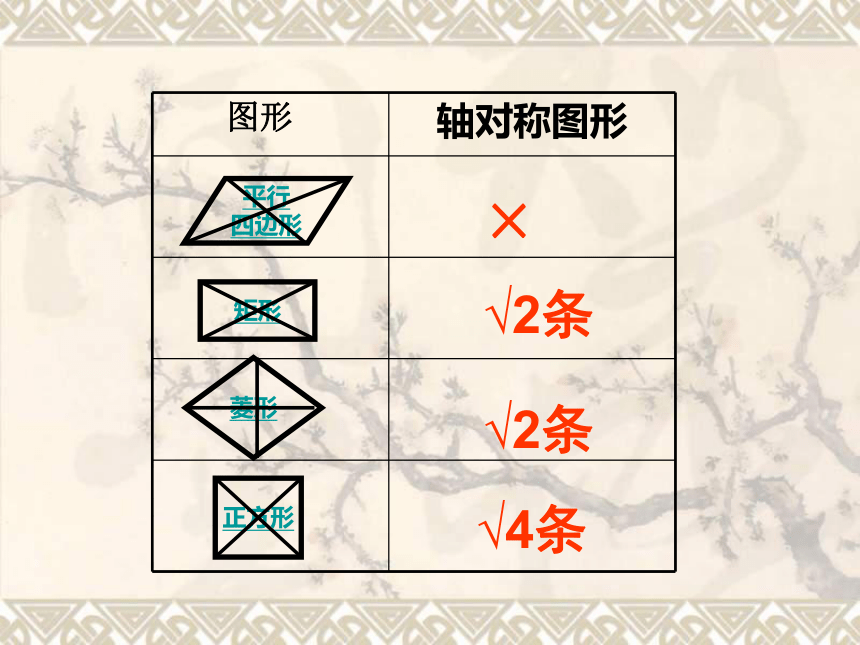
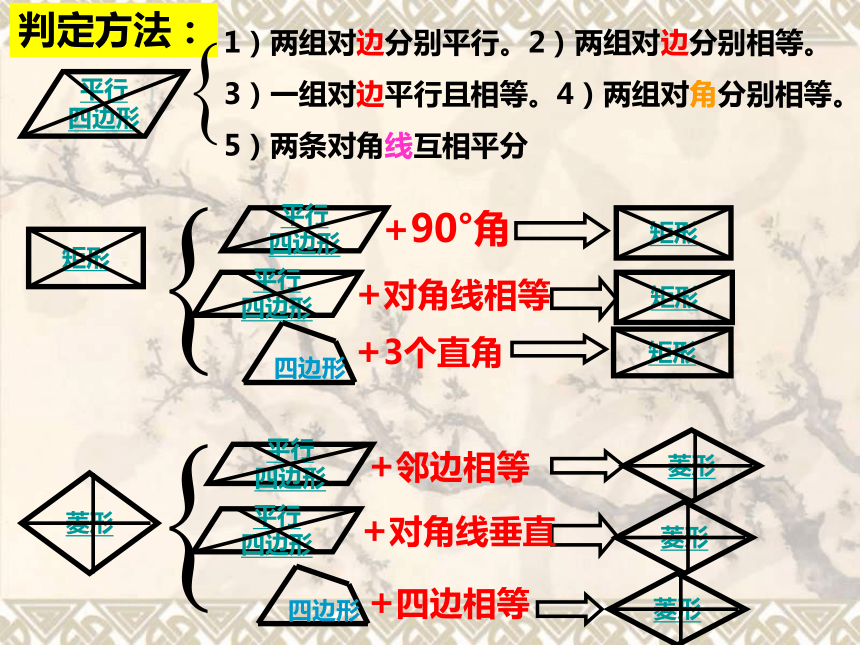
×√2条√2条√4条1)两组对边分别平行。2)两组对边分别相等。
3)一组对边平行且相等。4)两组对角分别相等。
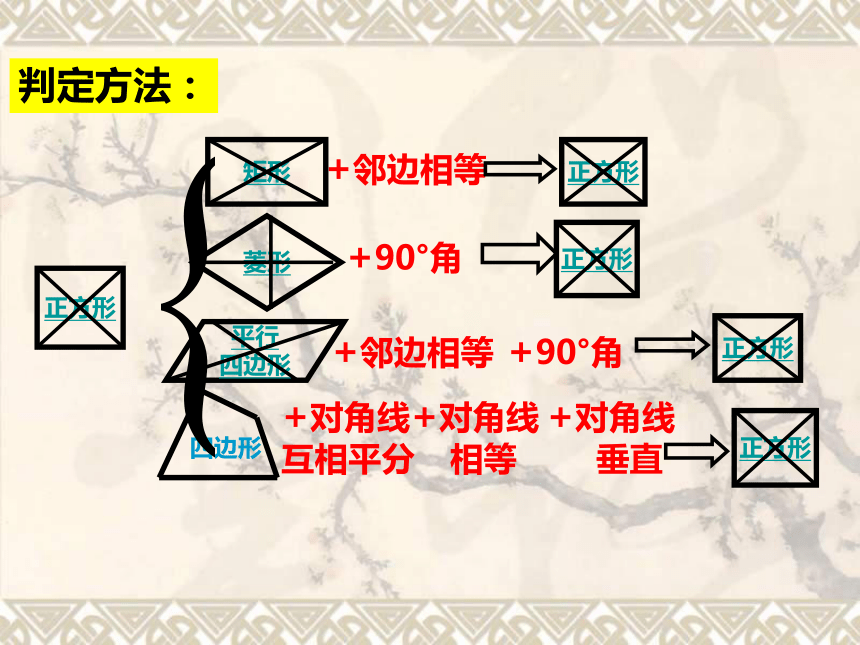
5)两条对角线互相平分判定方法:+邻边相等+90°角+对角线
互相平分+邻边相等+90°角+对角线
相等+对角线
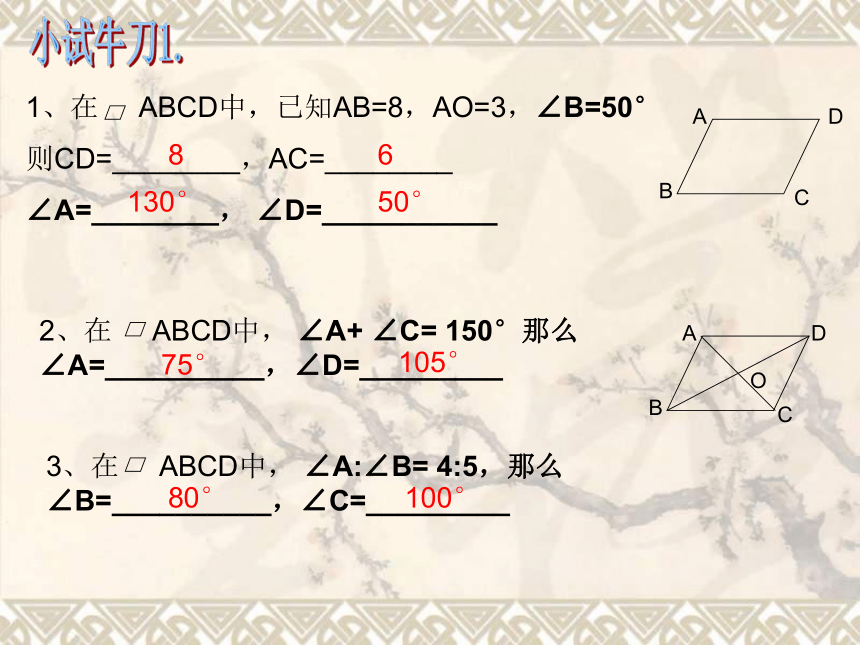
垂直判定方法:小试牛刀1.1、在 ABCD中,已知AB=8,AO=3,∠B=50°
则CD=________,AC=________
∠A=________, ∠D=___________2、在 ABCD中, ∠A+ ∠C= 150°那么
∠A=__________,∠D=_________ 3、在 ABCD中, ∠A:∠B= 4:5,那么
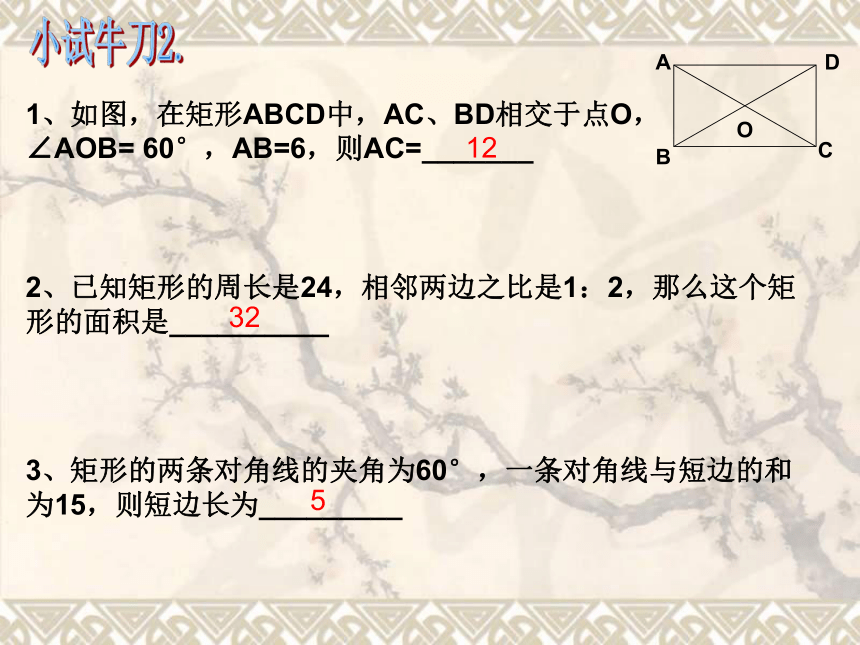
∠B=__________,∠C=_________ 8130° 675°50°105°80°100°1、如图,在矩形ABCD中,AC、BD相交于点O, ∠AOB= 60°,AB=6,则AC=_______小试牛刀2.2、已知矩形的周长是24,相邻两边之比是1:2,那么这个矩形的面积是__________3、矩形的两条对角线的夹角为60°,一条对角线与短边的和为15,则短边长为_________123254、(1)矩形具有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对边相等
C、对角线相等 D、对角线互相平分
(2)把一张长方形的纸条按图那样折叠,若得到
∠AME=70o ,则∠EMN=( )
A、45o B、50o
C、55o D、60o (3)如图,矩形ABCD沿AE折叠,使D点落在BC边上的F点处,
如果∠BAF=60°,那么∠DAE等于( )
A.15° B.30°
C.45° D.60° ACA1、如图,在菱形ABCD中,AB=10,OA=8,OB=6,则菱形的周长是_________,面积是___________ 2、如图,在菱形ABCD中, ∠B= 120°,则
∠DAC=___________3、菱形的一个内角为120°,较短的对角线长为10,那么菱形的周长是_____________964030°40小试牛刀3.4、(1)菱形有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对角线互相平分
C、对边平行且相等 D、对角线互相垂直(2)如图,小强拿一张正方形的纸(图(1)),沿虚线对折
一次得图(2),再对折一次得图(3),然后用剪刀沿图(3)
中的虚线剪成两部分,再把所得的三角形的部分打开后的
形状一定是( )
A.一般的平行四边形 B、菱形 C、矩形 D、正方形
(1)(2)(3)DB(1)对角线相等的四边形是矩形;
(2)对角线相等,且有一个角是直角的四边形是矩形;
(3)两条对角线垂直的四边形是菱形
(4)一条对角线平分一组对角的平行四边形是菱形
(5)四边相等的四边形是正方形
(6)对角线互相垂直平分的四边形是正方形×××√×菱形×菱形一、判断题:测一测1二、填空题:1、 ABCD的对角线AC与BD交于O,若
S ABCD=12cm2, S AOB=_______。 2、矩形对角线的交角为60°,一条对角线与
较短边的和为18cm, 则对角线长是______。 3、菱形的周长为16,高为2,则菱形相
邻的两角的 度数大小为______________。
4、菱形的对角线长为10和24,则周长
为_________。5、正方形ABCD中,E为BC上一点,且EF⊥
BD于F, 那么 △EFB是_______三角形。 3cm230°、150°12cm52等腰直角1、将矩形纸片ABCD、沿对角线AC折叠,
使B点落在E处。则EF与DF有什么关系?
试证明你的结论。
ABCDEF答:EF与DF是相等关系证明:矩形ABCD中:
∵ ∠B=∠E=∠D =90°
AB=AE=CD
又∵∠ AFE=∠CFD
∴ ΔAEF ≌ ΔCDF(AAS)
∴EF=DF
(全等三角形对应边相等)??三、解答题:2、已知 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。求证:PM=QN。2、已知 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。求证:PM=QN。2、已知 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。求证:PM=QN。如图,△ABC中,点O是AC上一个动点,过点O
作直线MN∥BC,设MN交∠BCA的平分线于点E,交
∠BCA的外角平分线于点F,
(1)、找出图形中相等的线段,并证明。
(2)、当点O运动到何处时,四边形AECF是矩形,
并证明你的结论。
(3)、当△ABC满足什么条件时,四边形AECF是正方形?OE=OF123当O运动到AC中点时,四边形AECF是矩形∠ACB=90°测一测2正方形ABCD的对角线相交于点O ,点 O是正方形
MNPO的一个顶点,如果两个正方形的边长相等,那么
正方形MNPO绕点O转动,试猜想两个正方形重叠
部分的面积四边形OEAF与正方形的面积有什么关系?
并证明你的结论。
0ABCDAMNPEF答:SOEAF =
SABCD有谁证明?测一测3ABCDOEF证明:正方形ABCD中:
∵ ∠EDO=∠ FAO=45°
DO=AO
∠ 1=90°–∠ 3=∠ 2
∴ △ DOE≌ △ AOF(ASA)
又∵ S四边形EAFO=S△ OEA+S△ AOF
∴ S四边形EAFO= S△ OEA +S△DOE
= S△ AOD = SABCD123(((45°45°
同学们再见!
(从定义观察)
正方形
矩形菱形平行四边形
有一个角是直角有一组邻边相等有一组邻边相等有一个角是直角几种平行四边形的特征比较 对边平行且相等对边平行且相等对边平行,
四条边都相等对边平行,
四条边相等对角相等,
邻角互补四个角都为直角对角相等,
邻角互补四个角都为直角对角线互相平分对角线相等
且互相平分对角线互相垂直平分,
每条对角线平分对角对角线互相垂直
平分且相等,
每条对角线平分对角
×√2条√2条√4条1)两组对边分别平行。2)两组对边分别相等。
3)一组对边平行且相等。4)两组对角分别相等。
5)两条对角线互相平分判定方法:+邻边相等+90°角+对角线
互相平分+邻边相等+90°角+对角线
相等+对角线
垂直判定方法:小试牛刀1.1、在 ABCD中,已知AB=8,AO=3,∠B=50°
则CD=________,AC=________
∠A=________, ∠D=___________2、在 ABCD中, ∠A+ ∠C= 150°那么
∠A=__________,∠D=_________ 3、在 ABCD中, ∠A:∠B= 4:5,那么
∠B=__________,∠C=_________ 8130° 675°50°105°80°100°1、如图,在矩形ABCD中,AC、BD相交于点O, ∠AOB= 60°,AB=6,则AC=_______小试牛刀2.2、已知矩形的周长是24,相邻两边之比是1:2,那么这个矩形的面积是__________3、矩形的两条对角线的夹角为60°,一条对角线与短边的和为15,则短边长为_________123254、(1)矩形具有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对边相等
C、对角线相等 D、对角线互相平分
(2)把一张长方形的纸条按图那样折叠,若得到
∠AME=70o ,则∠EMN=( )
A、45o B、50o
C、55o D、60o (3)如图,矩形ABCD沿AE折叠,使D点落在BC边上的F点处,
如果∠BAF=60°,那么∠DAE等于( )
A.15° B.30°
C.45° D.60° ACA1、如图,在菱形ABCD中,AB=10,OA=8,OB=6,则菱形的周长是_________,面积是___________ 2、如图,在菱形ABCD中, ∠B= 120°,则
∠DAC=___________3、菱形的一个内角为120°,较短的对角线长为10,那么菱形的周长是_____________964030°40小试牛刀3.4、(1)菱形有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对角线互相平分
C、对边平行且相等 D、对角线互相垂直(2)如图,小强拿一张正方形的纸(图(1)),沿虚线对折
一次得图(2),再对折一次得图(3),然后用剪刀沿图(3)
中的虚线剪成两部分,再把所得的三角形的部分打开后的
形状一定是( )
A.一般的平行四边形 B、菱形 C、矩形 D、正方形
(1)(2)(3)DB(1)对角线相等的四边形是矩形;
(2)对角线相等,且有一个角是直角的四边形是矩形;
(3)两条对角线垂直的四边形是菱形
(4)一条对角线平分一组对角的平行四边形是菱形
(5)四边相等的四边形是正方形
(6)对角线互相垂直平分的四边形是正方形×××√×菱形×菱形一、判断题:测一测1二、填空题:1、 ABCD的对角线AC与BD交于O,若
S ABCD=12cm2, S AOB=_______。 2、矩形对角线的交角为60°,一条对角线与
较短边的和为18cm, 则对角线长是______。 3、菱形的周长为16,高为2,则菱形相
邻的两角的 度数大小为______________。
4、菱形的对角线长为10和24,则周长
为_________。5、正方形ABCD中,E为BC上一点,且EF⊥
BD于F, 那么 △EFB是_______三角形。 3cm230°、150°12cm52等腰直角1、将矩形纸片ABCD、沿对角线AC折叠,
使B点落在E处。则EF与DF有什么关系?
试证明你的结论。
ABCDEF答:EF与DF是相等关系证明:矩形ABCD中:
∵ ∠B=∠E=∠D =90°
AB=AE=CD
又∵∠ AFE=∠CFD
∴ ΔAEF ≌ ΔCDF(AAS)
∴EF=DF
(全等三角形对应边相等)??三、解答题:2、已知 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。求证:PM=QN。2、已知 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。求证:PM=QN。2、已知 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。求证:PM=QN。如图,△ABC中,点O是AC上一个动点,过点O
作直线MN∥BC,设MN交∠BCA的平分线于点E,交
∠BCA的外角平分线于点F,
(1)、找出图形中相等的线段,并证明。
(2)、当点O运动到何处时,四边形AECF是矩形,
并证明你的结论。
(3)、当△ABC满足什么条件时,四边形AECF是正方形?OE=OF123当O运动到AC中点时,四边形AECF是矩形∠ACB=90°测一测2正方形ABCD的对角线相交于点O ,点 O是正方形
MNPO的一个顶点,如果两个正方形的边长相等,那么
正方形MNPO绕点O转动,试猜想两个正方形重叠
部分的面积四边形OEAF与正方形的面积有什么关系?
并证明你的结论。
0ABCDAMNPEF答:SOEAF =
SABCD有谁证明?测一测3ABCDOEF证明:正方形ABCD中:
∵ ∠EDO=∠ FAO=45°
DO=AO
∠ 1=90°–∠ 3=∠ 2
∴ △ DOE≌ △ AOF(ASA)
又∵ S四边形EAFO=S△ OEA+S△ AOF
∴ S四边形EAFO= S△ OEA +S△DOE
= S△ AOD = SABCD123(((45°45°
同学们再见!
