人教版八年级数学下册课件18.2 矩形的定义和性质
文档属性
| 名称 | 人教版八年级数学下册课件18.2 矩形的定义和性质 |  | |
| 格式 | zip | ||
| 文件大小 | 252.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-16 05:24:34 | ||
图片预览

文档简介
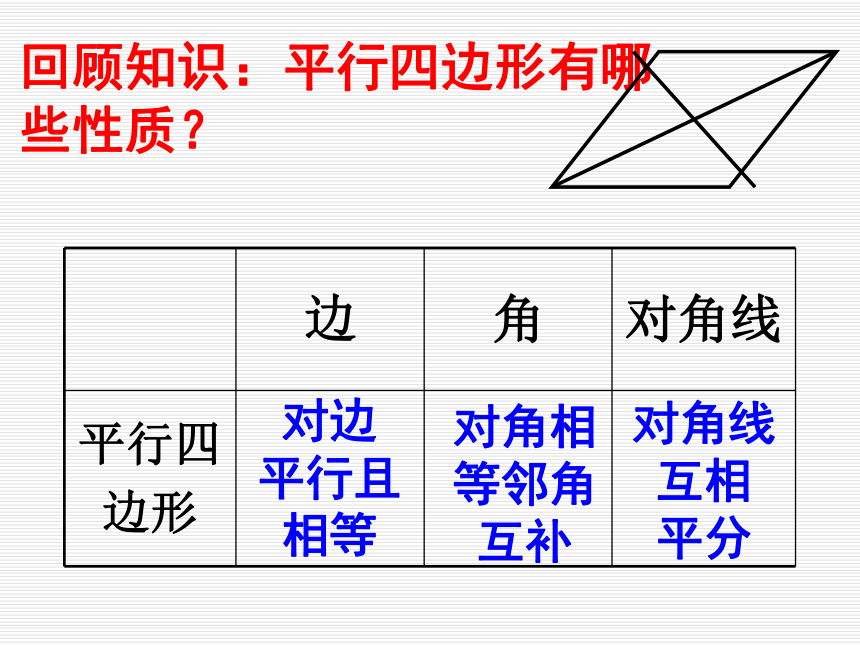
课件25张PPT。矩形第一课时回顾知识:平行四边形有哪些性质?对边
平行且
相等对角相等邻角互补对角线互相
平分
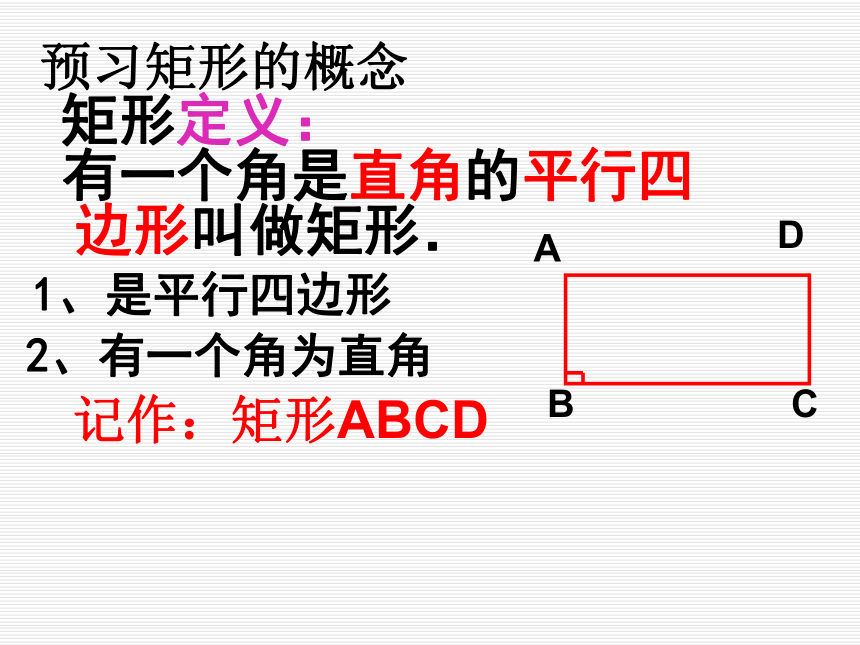
矩形定义:
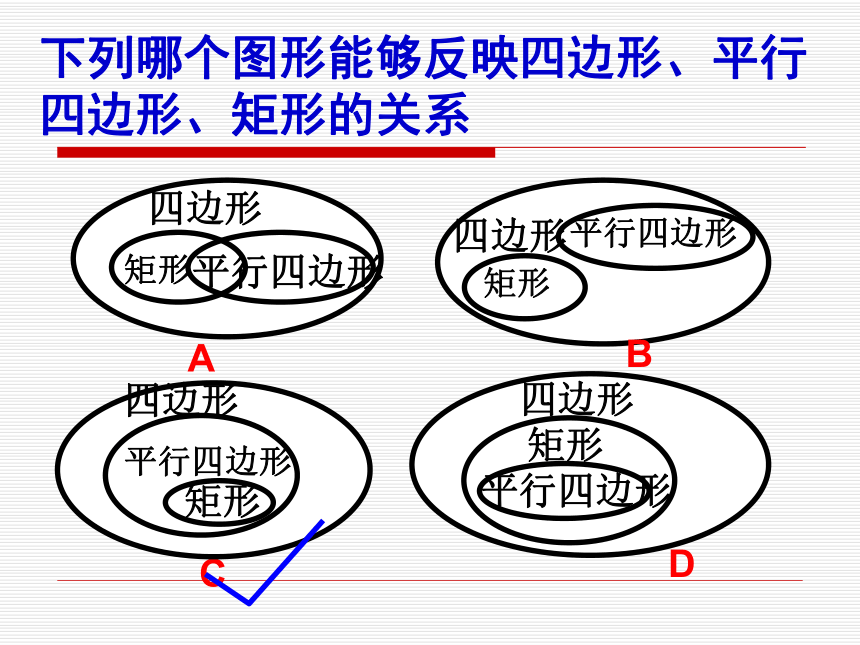
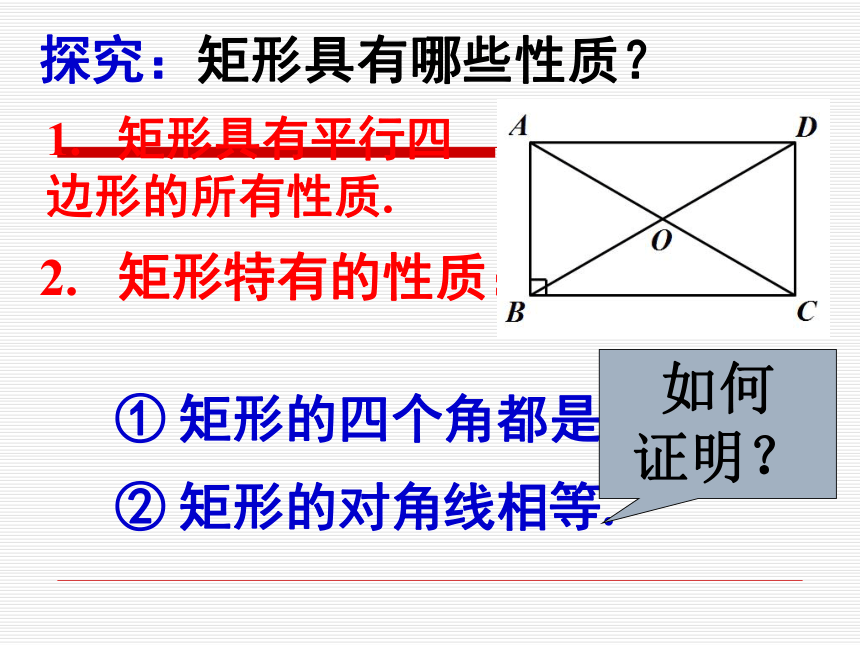
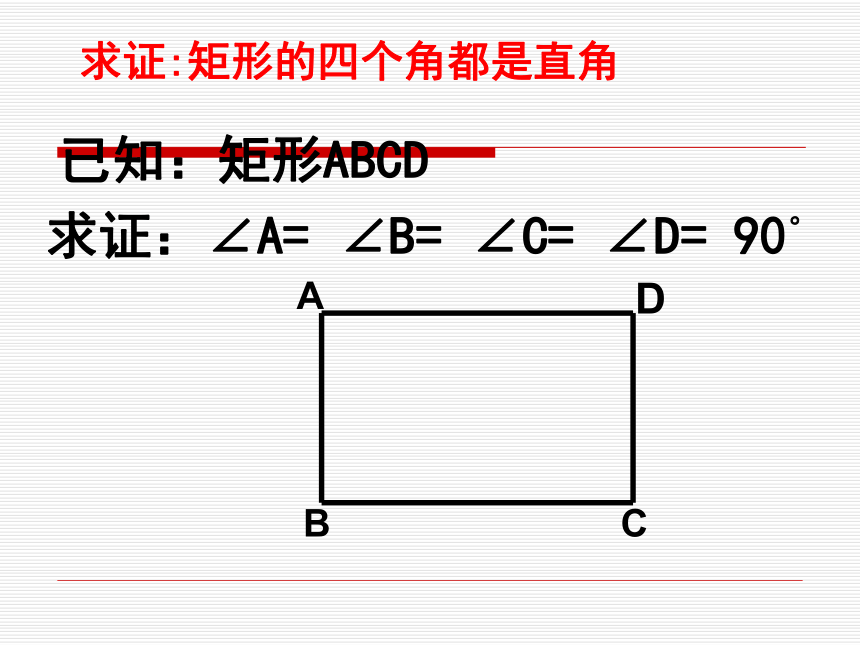
有一个角是直角的平行四边形叫做矩形.1、是平行四边形2、有一个角为直角记作:矩形ABCD预习矩形的概念下列哪个图形能够反映四边形、平行四边形、矩形的关系探究:矩形具有哪些性质?1. 矩形具有平行四边形的所有性质.2. 矩形特有的性质:① 矩形的四个角都是直角;② 矩形的对角线相等.如何
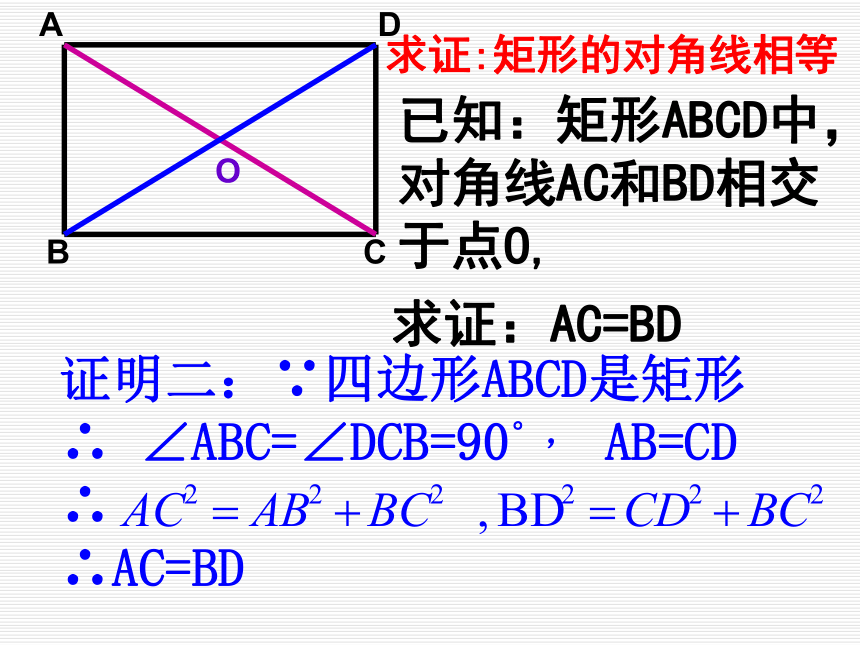
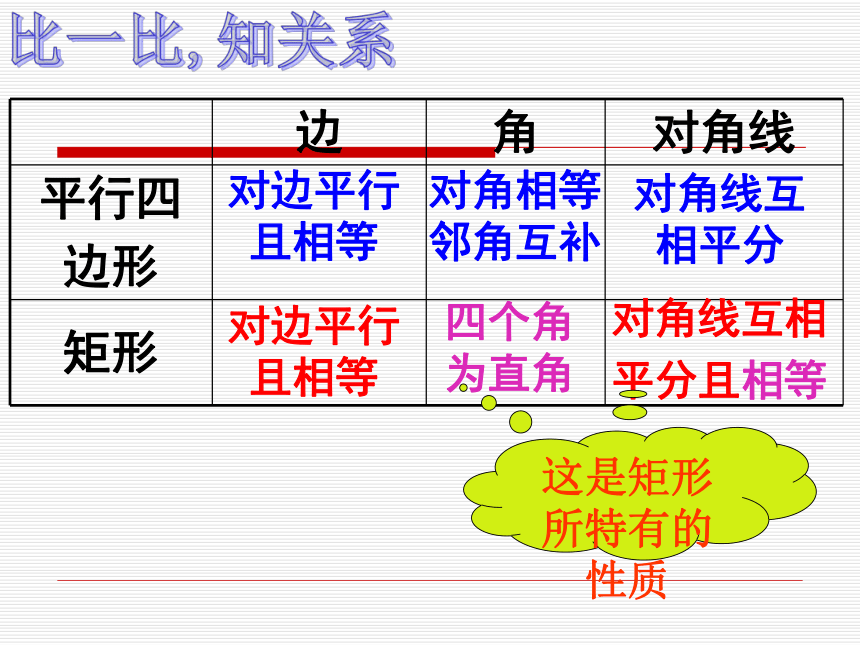
证明?求证:矩形的四个角都是直角已知:矩形ABCD求证:∠A= ∠B= ∠C= ∠D= 90°AODCB求证:矩形的对角线相等已知:矩形ABCD中,对角线AC和BD相交于点O,求证:AC=BD比一比,知关系对边平行
且相等对角相等
邻角互补对角线互
相平分对边平行
且相等四个角
为直角对角线互相
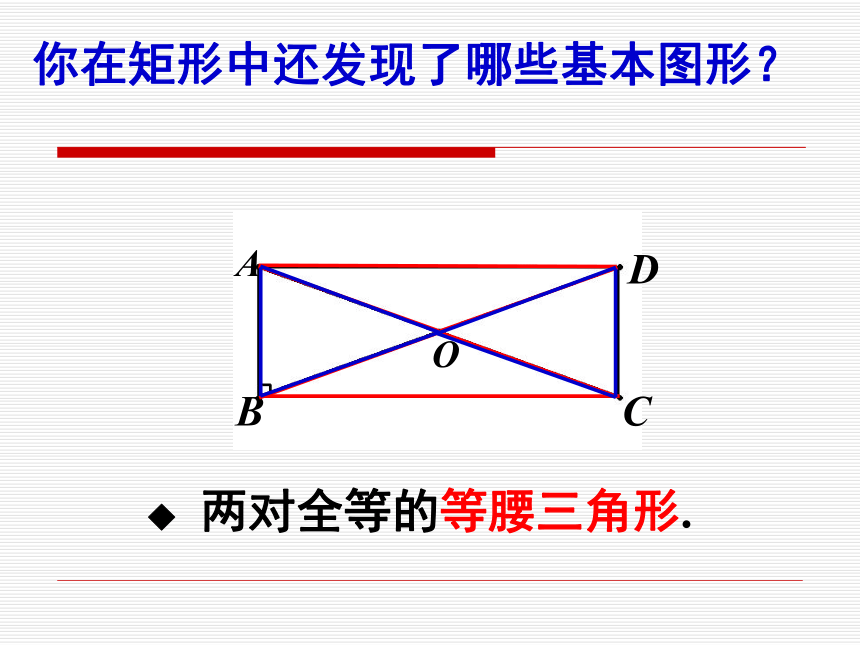
平分且相等◆ 两对全等的等腰三角形.你在矩形中还发现了哪些基本图形?◆ 四个全等的直角三角形.◆ 两对全等的等腰三角形.◆ 四个全等的直角三角形. 矩形的问题可以转化到直角三角形或等腰三角形来解决. 1. 矩形具有而一般平行四边形不具有的性质是( ).
A、对角线相等 B、对边相等
C、对角相等 D、对角线互相平分2、 矩形的一组邻边长分别是3cm和4cm,则它的对角线长是 cm. A5跟踪练习例1已知: 如图,矩形ABCD的两条对角线交于点O, AB=4cm ,∠AOB=60°。
求矩形对角线的长。 BODCA书P53例1书P53页:练习2、3O书P53页:练习2、31、如图,矩形ABCD的对角线的长为2,∠BDC=300,则矩形ABCD的面积为______.ADCB牛刀小试7.22、矩形ABCD中,AB=3.6cm,两条对角线相交于点O,∠AOD=2∠AOB,则对角线的长为_____cm. 3、矩形ABCD中,AC、BD相交于点O,AB=6,BC=8,则△ABO的周长为_____ADCBO16反馈:册64页64、如图,矩形ABCD中,AE平分∠BAD交BC于点E,ED=5cm,EC=3cm,求矩形的周长。解:∵四边形ABCD是矩形
∴∠C=∠B=∠BAD=90°,AB=DC注:解决矩形的有关问题时,常根据性质转化为直角三角形的有关问题进行解答.∵DE=5,EC=3
∴DC2=DE2-EC2=52-32,即:DC=4∵AE平分∠BAD
∴∠BAE=45°∴AB=BE=4∴BC=7∴矩形ABCD的周长为22cm矩形的定义和性质矩形的定义和性质3、在矩形中进行有关计算或证明,常根据矩形的性质将问题转化到直角三角形或等腰三角形中,利用直角三角形或等腰三角形的有关性质 进行解题。1、矩形定义:
有一个角是直角的平行四边形叫矩形矩形的对边平行且相等
矩形的四个角均为直角
2、矩形
矩形的对角线互相平分且相等小结作业 1、如图,把矩形纸片ABCD沿对角线AC折叠,点B落在点E处,EC与AD相交于点F.
(1)求证:△FAC是等腰三角形;
(2)若AB=4,BC=6,求△FAC的周长和面积.2、如图,在矩形ABCD中,AB=8,对角线BD比AD长4.求:① AD的长;
② 点A到BD的距离AE的长. 矩形的定义和性质4、在矩形中进行有关计算或证明,常根据矩形的性质将问题转化到直角三角形或等腰三角形中,利用直角三角形或等腰三角形的有关性质 进行解题。3、直角三角形的一个重要性质:斜边上的中线
等于斜边的一半;1、矩形定义:
有一个角是直角的平行四边形叫矩形矩形的对边平行且相等
矩形的四个角均为直角
2、矩形
矩形的对角线互相平分且相等歇闲小站2、如图,矩形AEFG和矩形ADCB的大小、形状完全相同,把它们拼成如图所示的L型图案,已知∠FAE=30°,分别求∠1、∠2的度数。 解:依题意可知:
∠FAE=∠DCA=30 °,AF=AC∴∠1=45 °,∴∠2=∠ACF-∠ACD=15 °∴∠DAC=60 °,∴∠FAC=90 °,矩形的定义和性质挑战你的思维 如图,△ABC为直角三角形,∠C=90°,现将补成矩形,使△ABC的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,那么符合要求的矩形可以画出两个,矩形ACBD和矩形AEFB
1)矩形ACBD和矩形AEFB的
面积有何数量关系?
2)如果△ABC是钝角三角形,
按短文中的要求把它补成矩形那么
符合要求的矩形可以画出几个?
试试看。
3)如果△ABC是锐角三角形呢?阅读下面短文矩形的定义和性质
平行且
相等对角相等邻角互补对角线互相
平分
矩形定义:
有一个角是直角的平行四边形叫做矩形.1、是平行四边形2、有一个角为直角记作:矩形ABCD预习矩形的概念下列哪个图形能够反映四边形、平行四边形、矩形的关系探究:矩形具有哪些性质?1. 矩形具有平行四边形的所有性质.2. 矩形特有的性质:① 矩形的四个角都是直角;② 矩形的对角线相等.如何
证明?求证:矩形的四个角都是直角已知:矩形ABCD求证:∠A= ∠B= ∠C= ∠D= 90°AODCB求证:矩形的对角线相等已知:矩形ABCD中,对角线AC和BD相交于点O,求证:AC=BD比一比,知关系对边平行
且相等对角相等
邻角互补对角线互
相平分对边平行
且相等四个角
为直角对角线互相
平分且相等◆ 两对全等的等腰三角形.你在矩形中还发现了哪些基本图形?◆ 四个全等的直角三角形.◆ 两对全等的等腰三角形.◆ 四个全等的直角三角形. 矩形的问题可以转化到直角三角形或等腰三角形来解决. 1. 矩形具有而一般平行四边形不具有的性质是( ).
A、对角线相等 B、对边相等
C、对角相等 D、对角线互相平分2、 矩形的一组邻边长分别是3cm和4cm,则它的对角线长是 cm. A5跟踪练习例1已知: 如图,矩形ABCD的两条对角线交于点O, AB=4cm ,∠AOB=60°。
求矩形对角线的长。 BODCA书P53例1书P53页:练习2、3O书P53页:练习2、31、如图,矩形ABCD的对角线的长为2,∠BDC=300,则矩形ABCD的面积为______.ADCB牛刀小试7.22、矩形ABCD中,AB=3.6cm,两条对角线相交于点O,∠AOD=2∠AOB,则对角线的长为_____cm. 3、矩形ABCD中,AC、BD相交于点O,AB=6,BC=8,则△ABO的周长为_____ADCBO16反馈:册64页64、如图,矩形ABCD中,AE平分∠BAD交BC于点E,ED=5cm,EC=3cm,求矩形的周长。解:∵四边形ABCD是矩形
∴∠C=∠B=∠BAD=90°,AB=DC注:解决矩形的有关问题时,常根据性质转化为直角三角形的有关问题进行解答.∵DE=5,EC=3
∴DC2=DE2-EC2=52-32,即:DC=4∵AE平分∠BAD
∴∠BAE=45°∴AB=BE=4∴BC=7∴矩形ABCD的周长为22cm矩形的定义和性质矩形的定义和性质3、在矩形中进行有关计算或证明,常根据矩形的性质将问题转化到直角三角形或等腰三角形中,利用直角三角形或等腰三角形的有关性质 进行解题。1、矩形定义:
有一个角是直角的平行四边形叫矩形矩形的对边平行且相等
矩形的四个角均为直角
2、矩形
矩形的对角线互相平分且相等小结作业 1、如图,把矩形纸片ABCD沿对角线AC折叠,点B落在点E处,EC与AD相交于点F.
(1)求证:△FAC是等腰三角形;
(2)若AB=4,BC=6,求△FAC的周长和面积.2、如图,在矩形ABCD中,AB=8,对角线BD比AD长4.求:① AD的长;
② 点A到BD的距离AE的长. 矩形的定义和性质4、在矩形中进行有关计算或证明,常根据矩形的性质将问题转化到直角三角形或等腰三角形中,利用直角三角形或等腰三角形的有关性质 进行解题。3、直角三角形的一个重要性质:斜边上的中线
等于斜边的一半;1、矩形定义:
有一个角是直角的平行四边形叫矩形矩形的对边平行且相等
矩形的四个角均为直角
2、矩形
矩形的对角线互相平分且相等歇闲小站2、如图,矩形AEFG和矩形ADCB的大小、形状完全相同,把它们拼成如图所示的L型图案,已知∠FAE=30°,分别求∠1、∠2的度数。 解:依题意可知:
∠FAE=∠DCA=30 °,AF=AC∴∠1=45 °,∴∠2=∠ACF-∠ACD=15 °∴∠DAC=60 °,∴∠FAC=90 °,矩形的定义和性质挑战你的思维 如图,△ABC为直角三角形,∠C=90°,现将补成矩形,使△ABC的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,那么符合要求的矩形可以画出两个,矩形ACBD和矩形AEFB
1)矩形ACBD和矩形AEFB的
面积有何数量关系?
2)如果△ABC是钝角三角形,
按短文中的要求把它补成矩形那么
符合要求的矩形可以画出几个?
试试看。
3)如果△ABC是锐角三角形呢?阅读下面短文矩形的定义和性质
