江苏省泰州市泰兴一中2015-2016学年高二(下)第二次段考数学试卷(文科)(解析版)
文档属性
| 名称 | 江苏省泰州市泰兴一中2015-2016学年高二(下)第二次段考数学试卷(文科)(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 148.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-15 00:00:00 | ||
图片预览




文档简介
2015-2016学年江苏省泰州市泰兴一中高二(下)第二次段考数学试卷(文科)
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题纸相应位置上.
1.已知全集U={0,1,2,3},集合A={0,1},B={1,2,3},则( UA)∩B= .
2.已知幂函数f(x)=k xα(k,α∈R)的图象过点(,),则k+α= .
3.某学校高一、高二、高三年级的学生人数之比为4:3:3,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为80的样本,则应从高一抽取的学生人数为 名.
4.从甲、乙、丙、丁4位同学中随机选出2名代表参加学校会议,则甲被选中的概率是 .
5.“α=”是“tanα=1”的 条件.(填“充分不必要”、“必要不充分”、“充要”或“既
不充分也不必要”)
6.如图是一个算法流程图,则输出S的值是 .
7.函数f(x)=ln(x2﹣3x+2)的单调减区间为 .
8.由命题“存在x∈R,使x2+2x+m≤0”是假命题,求得m的取值范围是(a,+∞),则实数a的值是 .
9.定义在R上的函数f(x),对任意x∈R都有f(x) f(x+1)=1,当x∈(﹣2,0)时,f(x)=4x,则f=x2﹣3x+a,若函数f(x)在区间(1,3)内有零点,则实数a的取值范围为 .
11.若f(x)=是R上的单调函数,则实数a的取值范围为 .
12.已知f(x)是定义在R上的偶函数,且对于任意的x∈[0,+∞),满足f(x+2)=f(x),若当x∈[0,2)时,f(x)=|x2﹣x﹣1|,则函数y=f(x)﹣1在区间[﹣2,4]上的零点个数为 .
13.已知函数当t∈[0,1]时,f(f(t))∈[0,1],则实数t的取值范围是 .
14.已知f(x)=,a∈R,对任意非零实数x1,存在唯一的非零实数x2(x1≠x2),使得f(x1)=f(x2)成立,则实数k的取值范围是 .
二、解答题:本大题共6小题,共90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
组号
分组
频数
频率
第一组
[230,235)
8
0.16
第二组
[235,240)
①
0.24
第三组
[240,245)
15
②
第四组
[245,250)
10
0.20
第五组
[250,255]
5
0.10
合
计
50
1.00
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
16.已知命题:“ x∈[﹣1,1],使等式m=x2﹣x成立”是真命题.
(1)求实数m的取值集合M;
(2)设不等式(x﹣a)[x﹣(2﹣a)]<0的解集为N,若N M,求a的取值范围.
17.已知二次函数f(x)有两个零点0和﹣2,且f(x)最小值是﹣1,函数g(x)与f(x)的图象关于原点对称.
(1)求f(x)和g(x)的解析式;
(2)若h(x)=f(x)﹣λg(x)在区间[﹣1,1]上是增函数,求实数λ的取值范围.
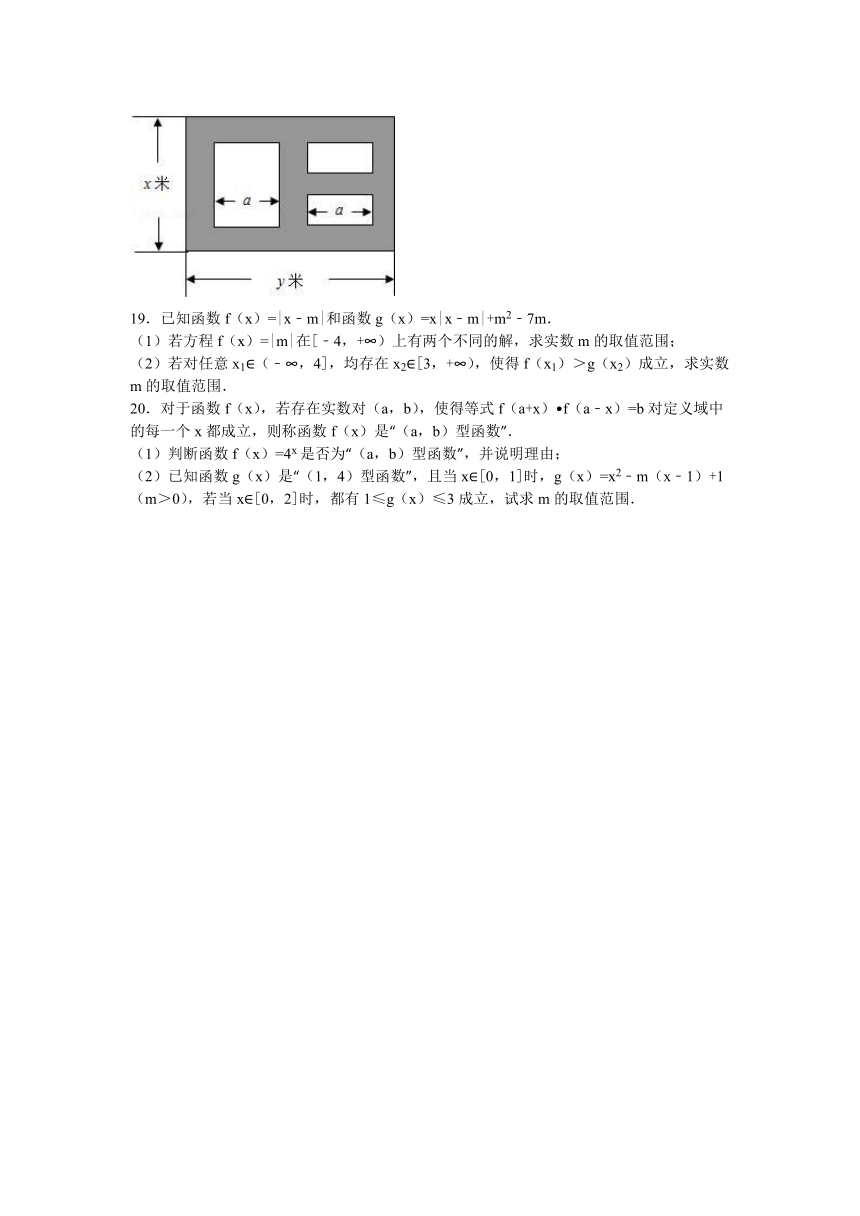
18.某市近郊有一块大约500m×500m的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
(1)分别用x表示y和S的函数关系式,并给出定义域;
(2)怎样设计能使S取得最大值,并求出最大值.
19.已知函数f(x)=|x﹣m|和函数g(x)=x|x﹣m|+m2﹣7m.
(1)若方程f(x)=|m|在[﹣4,+∞)上有两个不同的解,求实数m的取值范围;
(2)若对任意x1∈(﹣∞,4],均存在x2∈[3,+∞),使得f(x1)>g(x2)成立,求实数m的取值范围.
20.对于函数f(x),若存在实数对(a,b),使得等式f(a+x) f(a﹣x)=b对定义域中的每一个x都成立,则称函数f(x)是“(a,b)型函数”.
(1)判断函数f(x)=4x是否为“(a,b)型函数”,并说明理由;
(2)已知函数g(x)是“(1,4)型函数”,且当x∈[0,1]时,g(x)=x2﹣m(x﹣1)+1(m>0),若当x∈[0,2]时,都有1≤g(x)≤3成立,试求m的取值范围.
2015-2016学年江苏省泰州市泰兴一中高二(下)第二次段考数学试卷(文科)
参考答案与试题解析
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题纸相应位置上.
1.已知全集U={0,1,2,3},集合A={0,1},B={1,2,3},则( UA)∩B= {2,3} .
【考点】交、并、补集的混合运算.
【分析】直接利用补集和交集的运算进行求解即可得到答案.
【解答】解:由U={0,1,2,3},集合A={0,1},
∴ UA={2,3},又B={1,2,3},
∴( UA)∩B={2,3}∩{1,2,3}={2,3}.
故答案为:{2,3}.
2.已知幂函数f(x)=k xα(k,α∈R)的图象过点(,),则k+α= .
【考点】幂函数的概念、解析式、定义域、值域.
【分析】利用幂函数的定义求出k,利用函数的图象经过的点求出α,即可得到结果.
【解答】解:因为幂函数f(x)=k xα(k,α∈R)
由幂函数的定义可知k=1,
幂函数f(x)=k xα(k,α∈R)的图象过点(,),
所以,,
∴k+α==.
故答案为:.
3.某学校高一、高二、高三年级的学生人数之比为4:3:3,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为80的样本,则应从高一抽取的学生人数为 32 名.
【考点】分层抽样方法.
【分析】先求出高一学生在总体中所占的比例,再用样本容量乘以此比例,即得应从高一年级抽取的学生人数.
【解答】解:高一学生在总体中所占的比例为=,
故应从高一年级抽取的学生人数为80×=32,
故答案为:32.
4.从甲、乙、丙、丁4位同学中随机选出2名代表参加学校会议,则甲被选中的概率是 .
【考点】计数原理的应用.
【分析】求出从甲、乙、丙、丁4位同学中随机选出2名代表参加学校会议的基本事件,甲被选中的基本事件,即可求出甲被选中的概率.
【解答】解:从甲、乙、丙、丁4位同学中随机选出2名代表参加学校会议,共有=6种方法,
甲被选中,共有3种方法,
∴甲被选中的概率是=.
故答案为:.
5.“α=”是“tanα=1”的 充分不必要 条件.(填“充分不必要”、“必要不充分”、“充要”或“既
不充分也不必要”)
【考点】必要条件、充分条件与充要条件的判断.
【分析】根据充分条件、必要条件的概念,以及tanα=1时α的取值情况即可判断是tanα=1的什么条件.
【解答】解:时,tanα=1;
tanα=1时,,所以不一定得到;
∴是tanα=1的充分不必要条件.
故答案为:充分不必要.
6.如图是一个算法流程图,则输出S的值是 35 .
【考点】程序框图.
【分析】执行算法流程,写出每次循环得到的S,k的值,当k=7时满足条件k>5,输出S的值35.
【解答】解:执行算法流程,有
S=0,k=1
不满足条件k>5,S=1,k=3,
不满足条件k>5,S=10,k=5,
不满足条件k>5,S=35,k=7,
满足条件k>5,输出S的值35.
故答案为:35.
7.函数f(x)=ln(x2﹣3x+2)的单调减区间为 (﹣∞,1) .
【考点】复合函数的单调性.
【分析】求出函数的定义域,结合复合函数的单调性的关系进行求解即可.
【解答】解:由x2﹣3x+2>0得x>2或x<1,
设t=x2﹣3x+2,
则y═lnt为增函数,
要求函数f(x)=ln(x2﹣3x+2)的单调减区间,
即求函数t=x2﹣3x+2的递减区间,
∵t=x2﹣3x+2的递减区间为(﹣∞,1),
∴函数f(x)=ln(x2﹣3x+2)的单调减区间为(﹣∞,1),
故答案为:(﹣∞,1).
8.由命题“存在x∈R,使x2+2x+m≤0”是假命题,求得m的取值范围是(a,+∞),则实数a的值是 1 .
【考点】一元二次不等式的解法.
【分析】由题意知“任意x∈R,使x2+2x+m>0”是真命题,由二次函数的性质得△<0,求出m的范围,结合题意求出a的值.
【解答】解:∵“存在x∈R,使x2+2x+m≤0”是假命题,
∴“任意x∈R,使x2+2x+m>0”是真命题,
∴△=4﹣4m<0,解得m>1,
故a的值是1.
故答案为:1.
9.定义在R上的函数f(x),对任意x∈R都有f(x) f(x+1)=1,当x∈(﹣2,0)时,f(x)=4x,则f=f(x),利用函数的周期性,将条件进行转化即可得到结论.
【解答】解:对任意x∈R都有f(x) f(x+1)=1,可得f(x+2)==f(x),
∴f(x+2)=f(x),
函数f(x)是定义在R上是周期函数周期为2,
当x∈(﹣2,0)时,f(x)=4x,则f=f(﹣1)=4﹣1=
故答案为:.
10.设f(x)=x2﹣3x+a,若函数f(x)在区间(1,3)内有零点,则实数a的取值范围为 (0,] .
【考点】函数零点的判定定理;函数奇偶性的性质.
【分析】函数f(x)在区间(1,3)内有零点,即a=﹣x2+3x在x∈(1,3)上成立即可,转化出求函数的值域问题即可获得问题的解答.
【解答】解:函数f(x)在区间(1,3)内有零点,即a=﹣x2+3x在x∈(1,3)上成立,
∵a=﹣x2+3x=﹣(x﹣)2+,x∈(1,3)
∴a∈(0,].
故答案为:(0,].
11.若f(x)=是R上的单调函数,则实数a的取值范围为 [﹣,0) .
【考点】函数单调性的性质.
【分析】分f(x)是R上的减函数、增函数两种情况,分别求得实数a的取值范围,再取并集,即得所求.
【解答】解:若f(x)=是R上的单调减函数,则,求得﹣≤a<0.
若f(x)=是R上的单调增函数,则,求得a∈ ,
综上可得实数a的范围为[﹣,0),
故答案为:[﹣,0).
12.已知f(x)是定义在R上的偶函数,且对于任意的x∈[0,+∞),满足f(x+2)=f(x),若当x∈[0,2)时,f(x)=|x2﹣x﹣1|,则函数y=f(x)﹣1在区间[﹣2,4]上的零点个数为 7 .
【考点】函数零点的判定定理.
【分析】如图所示,y=g(x)=f(x)﹣1=,再利用f(x+2)=f(x),可得x∈[2,4]上的图象.由函数f(x)是R上的偶函数,可得g(x)也是R上的偶函数,结合图象即可得出零点个数.
【解答】解:如图所示,y=g(x)=f(x)﹣1=,
再利用f(x+2)=f(x),可得x∈[2,4]上的图象.
由函数f(x)是R上的偶函数,可得g(x)也是R上的偶函数,利用偶函数的性质可得x∈[﹣2,0)上的图象.
x∈[0,2)时,g(0)=g(1)=0,
x∈[2,4]时,g(2)=g(4)=g(0)=0,g(3)=g(1)=0.
x∈[﹣2,0)时,g(﹣2)=g(2)=0,g(﹣1)=g(1)=0.
指数可得:函数g(x)共有7个零点.
故答案为:7.
13.已知函数当t∈[0,1]时,f(f(t))∈[0,1],则实数t的取值范围是 .
【考点】函数与方程的综合运用.
【分析】通过t的范围,求出f(t)的表达式,判断f(t)的范围,然后代入已知函数,通过函数的值域求出t的范围即可.
【解答】解:因为t∈[0,1],所以f(t)=3t∈[1,3],
又函数,
所以f(f(t)=,因为f(f(t))∈[0,1],
所以
解得:,又t∈[0,1],
所以实数t的取值范围.
故答案为:.
14.已知f(x)=,a∈R,对任意非零实数x1,存在唯一的非零实数x2(x1≠x2),使得f(x1)=f(x2)成立,则实数k的取值范围是 (﹣∞,0]∪[8,+∞) .
【考点】分段函数的应用.
【分析】由题意结合函数图象可将问题转化为关于a的方程(3﹣a)2=k(1﹣a2)有实数解,解△≥0可得.
【解答】解:∵f(x)=)=,
∴当x=0时,f(x)=k(1﹣a2),
∵对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立.
∴函数必须为连续函数,∴(3﹣a)2=k(1﹣a2),
问题转化为(k+1)a2﹣6a+9﹣k=0有实数解,
∴△=62﹣4(k+1)(9﹣k)≥0,解得k≤0或k≥8.
故答案为:(﹣∞,0]∪[8,+∞).
二、解答题:本大题共6小题,共90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
组号
分组
频数
频率
第一组
[230,235)
8
0.16
第二组
[235,240)
①
0.24
第三组
[240,245)
15
②
第四组
[245,250)
10
0.20
第五组
[250,255]
5
0.10
合
计
50
1.00
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
【考点】等可能事件的概率;分层抽样方法;频率分布表.
【分析】(1)由频率分布表,可得①位置的数据为50﹣8﹣15﹣10﹣5=12,②位置的数据为1﹣0.16﹣0.24﹣0.20﹣0.1=0.3,即可得答案;
(2)读表可得,第三、四、五组分别有15、10、5人,共15+10+5=30人,要求从中用分层抽样法抽取6名学生,抽取比例为,由第三、四、五组的人数,计算可得答案;
(3)设(2)中选取的6人为abcdef(其中第四组的两人分别为d,e),记“2人中至少有一名是第四组”为事件A,用列举法列举从6人中任取2人的所有情形,进而可得事件A所含的基本事件的种数,由等可能事件的概率,计算可得答案.
【解答】解:(1)由频率分布表,可得①位置的数据为50﹣8﹣15﹣10﹣5=12,
②位置的数据为1﹣0.16﹣0.24﹣0.20﹣0.1=0.3,
故①②位置的数据分别为12、0.3;
(2)读表可得,第三、四、五组分别有15、10、5人,共15+10+5=30人,
要求从中用分层抽样法抽取6名学生,
则第三组参加考核人数为15×=3,
第四组参加考核人数为10×=2,
第五组参加考核人数为5×=1,
故第三、四、五组参加考核人数分别为3、2、1;
(3)设(2)中选取的6人为a、b、c、d、e、f(其中第四组的两人分别为d,e),
则从6人中任取2人的所有情形为:{ab,ac,ad,ae,af,bc,bd,be,bf,cd,ce,cf,de,df,ef}共有15种;
记“2人中至少有一名是第四组”为事件A,则事件A所含的基本事件的种数有9种.
所以,
故2人中至少有一名是第四组的概率为.
16.已知命题:“ x∈[﹣1,1],使等式m=x2﹣x成立”是真命题.
(1)求实数m的取值集合M;
(2)设不等式(x﹣a)[x﹣(2﹣a)]<0的解集为N,若N M,求a的取值范围.
【考点】集合的包含关系判断及应用;特称命题.
【分析】(1)若方程m=x2﹣x在[﹣1,1]上有解,即m的取值范围为函数y=x2﹣x在[﹣1,1]上的值域,结合二次函数的图象和性质,要得M;
(2)对a的取值进行分类讨论,求出不等式(x﹣a)[x﹣(2﹣a)]<0的解集为N,结合N M,可得a的取值范围.
【解答】解:(1)由题意知,方程m=x2﹣x在[﹣1,1]上有解,
即m的取值范围为函数y=x2﹣x在[﹣1,1]上的值域,
由函数y=x2﹣x的图象是开口朝上,且以直线x=为对称轴的抛物线,
故当x=时,函数最小值为﹣,当x=﹣1时,函数最大值为2,
故m=[﹣,2],
(2)当a=1时,解集N为空集,满足题意;
当a>1时,a>2﹣a,此时集合N={x|2﹣a<x<a},则1<a≤2
当a<1时,a<2﹣a,此时集合N={x|a<x<2﹣a},则0≤a<1
综上:0≤a≤2
17.已知二次函数f(x)有两个零点0和﹣2,且f(x)最小值是﹣1,函数g(x)与f(x)的图象关于原点对称.
(1)求f(x)和g(x)的解析式;
(2)若h(x)=f(x)﹣λg(x)在区间[﹣1,1]上是增函数,求实数λ的取值范围.
【考点】函数的零点;函数解析式的求解及常用方法;函数单调性的判断与证明.
【分析】(1)根据二次函数的零点,利用待定系数法即可求f(x)和g(x)的解析式;
(2)根据h(x)=f(x)﹣λg(x)在区间[﹣1,1]上是增函数,确定对称轴和对应区间之间的关系,即可求实数λ的取值范围.
【解答】解:(1)∵二次函数f(x)有两个零点0和﹣2,
∴设f(x)=ax(x+2)=ax2+2ax(a>0).f(x)图象的对称轴是x=﹣1,
∴f(﹣1)=﹣1,即a﹣2a=﹣1,
∴a=1,
∴f(x)=x2+2x.
∵函数g(x)的图象与f(x)的图象关于原点对称,
∴g(x)=﹣f(﹣x)=﹣x2+2x.
(2)由(1)得h(x)=x2+2x﹣λ(﹣x2+2x)=(λ+1)x2+2(1﹣λ)x.
①当λ=﹣1时,h(x)=4x满足在区间[﹣1,1]上是增函数;
②当λ<﹣1时,h(x)图象对称轴是x=
则≥1,
又λ<﹣1,解得λ<﹣1;
③当λ>﹣1时,同理需≤﹣1,
又λ>﹣1,解得﹣1<λ≤0.
综上,满足条件的实数λ的取值范围是(﹣∞,0].
18.某市近郊有一块大约500m×500m的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
(1)分别用x表示y和S的函数关系式,并给出定义域;
(2)怎样设计能使S取得最大值,并求出最大值.
【考点】函数模型的选择与应用.
【分析】(1)总面积为xy=3000,且2a+6=y,则y=,(其中6<x<500),从而运动场占地面积为S=(x﹣4)a+(x﹣6)a,代入整理即得;
(2)由(1)知,占地面积S=3030﹣6x﹣=3030﹣(6x+),由基本不等式可得函数的最大值,以及对应的x的值.
【解答】解:(1)由已知xy=3000,∴,其定义域是(6,500).
S=(x﹣4)a+(x﹣6)a=(2x﹣10)a,
∵2a+6=y,∴,
∴,其定义域是(6,500).
(2),
当且仅当,即x=50∈(6,500)时,上述不等式等号成立,
此时,x=50,y=60,Smax=2430.
答:设计x=50m,y=60m时,运动场地面积最大,最大值为2430平方米.
19.已知函数f(x)=|x﹣m|和函数g(x)=x|x﹣m|+m2﹣7m.
(1)若方程f(x)=|m|在[﹣4,+∞)上有两个不同的解,求实数m的取值范围;
(2)若对任意x1∈(﹣∞,4],均存在x2∈[3,+∞),使得f(x1)>g(x2)成立,求实数m的取值范围.
【考点】带绝对值的函数;函数的最值及其几何意义;根的存在性及根的个数判断.
【分析】(1)解方程f(x)=|m|,解得x=0,或x=2m.由题意可得
2m≥﹣4,且2m≠0,由此求得实数m的取值范围.
(2)命题等价于任意x1∈(﹣∞,4],任意的x2∈[3,+∞),fmin(x1)>gmin(x2)
成立,分m<3、
3≤m<4、4≤m三种情况,分别求出实数m的取值范围再取并集,即得所求.
【解答】解:(1)方程f(x)=|m|,即|x﹣m|=|m|,解得x=0,或x=2m.
要使方程|x﹣m|=|m|在[﹣4,+∞)上有两个不同的解,
需
2m≥﹣4,且2m≠0.解得
m≥﹣2
且m≠0.
故实数m的取值范围为[﹣2,0)∪(0,+∞).
(2)由于对任意x1∈(﹣∞,4],都存在x2∈[3,+∞),使f(x1)>g(x2)成立,
故有
fmin(x1)>gmin(x2)
成立.
又函数f(x)=|x﹣m|=,故fmin(x1)=.
又函数g(x)=x|x﹣m|+m2﹣7m=,
故gmin(x2)=.
当m<3时,有0>m2﹣10m+9,解得
1<m<3.
当
3≤m<4,有0>m2﹣7m,解得
3≤m<4.
当4≤m,有m﹣4>m2﹣7m,解得
4≤m<4+2.
综上可得,1<m<4+2,故实数m的取值范围为(1,4+2
).
20.对于函数f(x),若存在实数对(a,b),使得等式f(a+x) f(a﹣x)=b对定义域中的每一个x都成立,则称函数f(x)是“(a,b)型函数”.
(1)判断函数f(x)=4x是否为“(a,b)型函数”,并说明理由;
(2)已知函数g(x)是“(1,4)型函数”,且当x∈[0,1]时,g(x)=x2﹣m(x﹣1)+1(m>0),若当x∈[0,2]时,都有1≤g(x)≤3成立,试求m的取值范围.
【考点】函数与方程的综合运用;抽象函数及其应用.
【分析】(1)利用定义,直接判断求解即可.
(2)由题意得,g(1+x)g(1﹣x)=4,所以当x∈[1,2]时,,其中2﹣x∈[0,1],
而x∈[0,1]时,g(x)=x2+m(1﹣x)+1=x2﹣mx+m+1>0,且其对称轴方程为,通过①当,②当,③当,求出函数的值域,然后推出所求m的取值范围.
【解答】解:(1)函数f(x)=4x是“(a,b)型函数”…
因为由f(a+x) f(a﹣x)=b,得16a=b,所以存在这样的实数对,如a=1,b=16…
(2)由题意得,g(1+x)g(1﹣x)=4,所以当x∈[1,2]时,,其中2﹣x∈[0,1],
而x∈[0,1]时,g(x)=x2+m(1﹣x)+1=x2﹣mx+m+1>0,且其对称轴方程为,
①当,即m>2时,g(x)在[0,1]上的值域为[g(1),g(0)],即[2,m+1],则g(x)在[0,2]上的值域为,由题意得,此时无解…
②当,即1≤m≤2时,g(x)的值域为,即,所以则g(x)在[0,2]上的值域为,则由题意得且,
解得1≤m≤2…
③当,即0<m≤1时,g(x)的值域为,即,则g(x)在[0,2]上的值域为=,
则,解得.
综上所述,所求m的取值范围是…
2016年10月15日
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题纸相应位置上.
1.已知全集U={0,1,2,3},集合A={0,1},B={1,2,3},则( UA)∩B= .
2.已知幂函数f(x)=k xα(k,α∈R)的图象过点(,),则k+α= .
3.某学校高一、高二、高三年级的学生人数之比为4:3:3,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为80的样本,则应从高一抽取的学生人数为 名.
4.从甲、乙、丙、丁4位同学中随机选出2名代表参加学校会议,则甲被选中的概率是 .
5.“α=”是“tanα=1”的 条件.(填“充分不必要”、“必要不充分”、“充要”或“既
不充分也不必要”)
6.如图是一个算法流程图,则输出S的值是 .
7.函数f(x)=ln(x2﹣3x+2)的单调减区间为 .
8.由命题“存在x∈R,使x2+2x+m≤0”是假命题,求得m的取值范围是(a,+∞),则实数a的值是 .
9.定义在R上的函数f(x),对任意x∈R都有f(x) f(x+1)=1,当x∈(﹣2,0)时,f(x)=4x,则f=x2﹣3x+a,若函数f(x)在区间(1,3)内有零点,则实数a的取值范围为 .
11.若f(x)=是R上的单调函数,则实数a的取值范围为 .
12.已知f(x)是定义在R上的偶函数,且对于任意的x∈[0,+∞),满足f(x+2)=f(x),若当x∈[0,2)时,f(x)=|x2﹣x﹣1|,则函数y=f(x)﹣1在区间[﹣2,4]上的零点个数为 .
13.已知函数当t∈[0,1]时,f(f(t))∈[0,1],则实数t的取值范围是 .
14.已知f(x)=,a∈R,对任意非零实数x1,存在唯一的非零实数x2(x1≠x2),使得f(x1)=f(x2)成立,则实数k的取值范围是 .
二、解答题:本大题共6小题,共90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
组号
分组
频数
频率
第一组
[230,235)
8
0.16
第二组
[235,240)
①
0.24
第三组
[240,245)
15
②
第四组
[245,250)
10
0.20
第五组
[250,255]
5
0.10
合
计
50
1.00
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
16.已知命题:“ x∈[﹣1,1],使等式m=x2﹣x成立”是真命题.
(1)求实数m的取值集合M;
(2)设不等式(x﹣a)[x﹣(2﹣a)]<0的解集为N,若N M,求a的取值范围.
17.已知二次函数f(x)有两个零点0和﹣2,且f(x)最小值是﹣1,函数g(x)与f(x)的图象关于原点对称.
(1)求f(x)和g(x)的解析式;
(2)若h(x)=f(x)﹣λg(x)在区间[﹣1,1]上是增函数,求实数λ的取值范围.
18.某市近郊有一块大约500m×500m的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
(1)分别用x表示y和S的函数关系式,并给出定义域;
(2)怎样设计能使S取得最大值,并求出最大值.
19.已知函数f(x)=|x﹣m|和函数g(x)=x|x﹣m|+m2﹣7m.
(1)若方程f(x)=|m|在[﹣4,+∞)上有两个不同的解,求实数m的取值范围;
(2)若对任意x1∈(﹣∞,4],均存在x2∈[3,+∞),使得f(x1)>g(x2)成立,求实数m的取值范围.
20.对于函数f(x),若存在实数对(a,b),使得等式f(a+x) f(a﹣x)=b对定义域中的每一个x都成立,则称函数f(x)是“(a,b)型函数”.
(1)判断函数f(x)=4x是否为“(a,b)型函数”,并说明理由;
(2)已知函数g(x)是“(1,4)型函数”,且当x∈[0,1]时,g(x)=x2﹣m(x﹣1)+1(m>0),若当x∈[0,2]时,都有1≤g(x)≤3成立,试求m的取值范围.
2015-2016学年江苏省泰州市泰兴一中高二(下)第二次段考数学试卷(文科)
参考答案与试题解析
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题纸相应位置上.
1.已知全集U={0,1,2,3},集合A={0,1},B={1,2,3},则( UA)∩B= {2,3} .
【考点】交、并、补集的混合运算.
【分析】直接利用补集和交集的运算进行求解即可得到答案.
【解答】解:由U={0,1,2,3},集合A={0,1},
∴ UA={2,3},又B={1,2,3},
∴( UA)∩B={2,3}∩{1,2,3}={2,3}.
故答案为:{2,3}.
2.已知幂函数f(x)=k xα(k,α∈R)的图象过点(,),则k+α= .
【考点】幂函数的概念、解析式、定义域、值域.
【分析】利用幂函数的定义求出k,利用函数的图象经过的点求出α,即可得到结果.
【解答】解:因为幂函数f(x)=k xα(k,α∈R)
由幂函数的定义可知k=1,
幂函数f(x)=k xα(k,α∈R)的图象过点(,),
所以,,
∴k+α==.
故答案为:.
3.某学校高一、高二、高三年级的学生人数之比为4:3:3,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为80的样本,则应从高一抽取的学生人数为 32 名.
【考点】分层抽样方法.
【分析】先求出高一学生在总体中所占的比例,再用样本容量乘以此比例,即得应从高一年级抽取的学生人数.
【解答】解:高一学生在总体中所占的比例为=,
故应从高一年级抽取的学生人数为80×=32,
故答案为:32.
4.从甲、乙、丙、丁4位同学中随机选出2名代表参加学校会议,则甲被选中的概率是 .
【考点】计数原理的应用.
【分析】求出从甲、乙、丙、丁4位同学中随机选出2名代表参加学校会议的基本事件,甲被选中的基本事件,即可求出甲被选中的概率.
【解答】解:从甲、乙、丙、丁4位同学中随机选出2名代表参加学校会议,共有=6种方法,
甲被选中,共有3种方法,
∴甲被选中的概率是=.
故答案为:.
5.“α=”是“tanα=1”的 充分不必要 条件.(填“充分不必要”、“必要不充分”、“充要”或“既
不充分也不必要”)
【考点】必要条件、充分条件与充要条件的判断.
【分析】根据充分条件、必要条件的概念,以及tanα=1时α的取值情况即可判断是tanα=1的什么条件.
【解答】解:时,tanα=1;
tanα=1时,,所以不一定得到;
∴是tanα=1的充分不必要条件.
故答案为:充分不必要.
6.如图是一个算法流程图,则输出S的值是 35 .
【考点】程序框图.
【分析】执行算法流程,写出每次循环得到的S,k的值,当k=7时满足条件k>5,输出S的值35.
【解答】解:执行算法流程,有
S=0,k=1
不满足条件k>5,S=1,k=3,
不满足条件k>5,S=10,k=5,
不满足条件k>5,S=35,k=7,
满足条件k>5,输出S的值35.
故答案为:35.
7.函数f(x)=ln(x2﹣3x+2)的单调减区间为 (﹣∞,1) .
【考点】复合函数的单调性.
【分析】求出函数的定义域,结合复合函数的单调性的关系进行求解即可.
【解答】解:由x2﹣3x+2>0得x>2或x<1,
设t=x2﹣3x+2,
则y═lnt为增函数,
要求函数f(x)=ln(x2﹣3x+2)的单调减区间,
即求函数t=x2﹣3x+2的递减区间,
∵t=x2﹣3x+2的递减区间为(﹣∞,1),
∴函数f(x)=ln(x2﹣3x+2)的单调减区间为(﹣∞,1),
故答案为:(﹣∞,1).
8.由命题“存在x∈R,使x2+2x+m≤0”是假命题,求得m的取值范围是(a,+∞),则实数a的值是 1 .
【考点】一元二次不等式的解法.
【分析】由题意知“任意x∈R,使x2+2x+m>0”是真命题,由二次函数的性质得△<0,求出m的范围,结合题意求出a的值.
【解答】解:∵“存在x∈R,使x2+2x+m≤0”是假命题,
∴“任意x∈R,使x2+2x+m>0”是真命题,
∴△=4﹣4m<0,解得m>1,
故a的值是1.
故答案为:1.
9.定义在R上的函数f(x),对任意x∈R都有f(x) f(x+1)=1,当x∈(﹣2,0)时,f(x)=4x,则f=f(x),利用函数的周期性,将条件进行转化即可得到结论.
【解答】解:对任意x∈R都有f(x) f(x+1)=1,可得f(x+2)==f(x),
∴f(x+2)=f(x),
函数f(x)是定义在R上是周期函数周期为2,
当x∈(﹣2,0)时,f(x)=4x,则f=f(﹣1)=4﹣1=
故答案为:.
10.设f(x)=x2﹣3x+a,若函数f(x)在区间(1,3)内有零点,则实数a的取值范围为 (0,] .
【考点】函数零点的判定定理;函数奇偶性的性质.
【分析】函数f(x)在区间(1,3)内有零点,即a=﹣x2+3x在x∈(1,3)上成立即可,转化出求函数的值域问题即可获得问题的解答.
【解答】解:函数f(x)在区间(1,3)内有零点,即a=﹣x2+3x在x∈(1,3)上成立,
∵a=﹣x2+3x=﹣(x﹣)2+,x∈(1,3)
∴a∈(0,].
故答案为:(0,].
11.若f(x)=是R上的单调函数,则实数a的取值范围为 [﹣,0) .
【考点】函数单调性的性质.
【分析】分f(x)是R上的减函数、增函数两种情况,分别求得实数a的取值范围,再取并集,即得所求.
【解答】解:若f(x)=是R上的单调减函数,则,求得﹣≤a<0.
若f(x)=是R上的单调增函数,则,求得a∈ ,
综上可得实数a的范围为[﹣,0),
故答案为:[﹣,0).
12.已知f(x)是定义在R上的偶函数,且对于任意的x∈[0,+∞),满足f(x+2)=f(x),若当x∈[0,2)时,f(x)=|x2﹣x﹣1|,则函数y=f(x)﹣1在区间[﹣2,4]上的零点个数为 7 .
【考点】函数零点的判定定理.
【分析】如图所示,y=g(x)=f(x)﹣1=,再利用f(x+2)=f(x),可得x∈[2,4]上的图象.由函数f(x)是R上的偶函数,可得g(x)也是R上的偶函数,结合图象即可得出零点个数.
【解答】解:如图所示,y=g(x)=f(x)﹣1=,
再利用f(x+2)=f(x),可得x∈[2,4]上的图象.
由函数f(x)是R上的偶函数,可得g(x)也是R上的偶函数,利用偶函数的性质可得x∈[﹣2,0)上的图象.
x∈[0,2)时,g(0)=g(1)=0,
x∈[2,4]时,g(2)=g(4)=g(0)=0,g(3)=g(1)=0.
x∈[﹣2,0)时,g(﹣2)=g(2)=0,g(﹣1)=g(1)=0.
指数可得:函数g(x)共有7个零点.
故答案为:7.
13.已知函数当t∈[0,1]时,f(f(t))∈[0,1],则实数t的取值范围是 .
【考点】函数与方程的综合运用.
【分析】通过t的范围,求出f(t)的表达式,判断f(t)的范围,然后代入已知函数,通过函数的值域求出t的范围即可.
【解答】解:因为t∈[0,1],所以f(t)=3t∈[1,3],
又函数,
所以f(f(t)=,因为f(f(t))∈[0,1],
所以
解得:,又t∈[0,1],
所以实数t的取值范围.
故答案为:.
14.已知f(x)=,a∈R,对任意非零实数x1,存在唯一的非零实数x2(x1≠x2),使得f(x1)=f(x2)成立,则实数k的取值范围是 (﹣∞,0]∪[8,+∞) .
【考点】分段函数的应用.
【分析】由题意结合函数图象可将问题转化为关于a的方程(3﹣a)2=k(1﹣a2)有实数解,解△≥0可得.
【解答】解:∵f(x)=)=,
∴当x=0时,f(x)=k(1﹣a2),
∵对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立.
∴函数必须为连续函数,∴(3﹣a)2=k(1﹣a2),
问题转化为(k+1)a2﹣6a+9﹣k=0有实数解,
∴△=62﹣4(k+1)(9﹣k)≥0,解得k≤0或k≥8.
故答案为:(﹣∞,0]∪[8,+∞).
二、解答题:本大题共6小题,共90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
组号
分组
频数
频率
第一组
[230,235)
8
0.16
第二组
[235,240)
①
0.24
第三组
[240,245)
15
②
第四组
[245,250)
10
0.20
第五组
[250,255]
5
0.10
合
计
50
1.00
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
【考点】等可能事件的概率;分层抽样方法;频率分布表.
【分析】(1)由频率分布表,可得①位置的数据为50﹣8﹣15﹣10﹣5=12,②位置的数据为1﹣0.16﹣0.24﹣0.20﹣0.1=0.3,即可得答案;
(2)读表可得,第三、四、五组分别有15、10、5人,共15+10+5=30人,要求从中用分层抽样法抽取6名学生,抽取比例为,由第三、四、五组的人数,计算可得答案;
(3)设(2)中选取的6人为abcdef(其中第四组的两人分别为d,e),记“2人中至少有一名是第四组”为事件A,用列举法列举从6人中任取2人的所有情形,进而可得事件A所含的基本事件的种数,由等可能事件的概率,计算可得答案.
【解答】解:(1)由频率分布表,可得①位置的数据为50﹣8﹣15﹣10﹣5=12,
②位置的数据为1﹣0.16﹣0.24﹣0.20﹣0.1=0.3,
故①②位置的数据分别为12、0.3;
(2)读表可得,第三、四、五组分别有15、10、5人,共15+10+5=30人,
要求从中用分层抽样法抽取6名学生,
则第三组参加考核人数为15×=3,
第四组参加考核人数为10×=2,
第五组参加考核人数为5×=1,
故第三、四、五组参加考核人数分别为3、2、1;
(3)设(2)中选取的6人为a、b、c、d、e、f(其中第四组的两人分别为d,e),
则从6人中任取2人的所有情形为:{ab,ac,ad,ae,af,bc,bd,be,bf,cd,ce,cf,de,df,ef}共有15种;
记“2人中至少有一名是第四组”为事件A,则事件A所含的基本事件的种数有9种.
所以,
故2人中至少有一名是第四组的概率为.
16.已知命题:“ x∈[﹣1,1],使等式m=x2﹣x成立”是真命题.
(1)求实数m的取值集合M;
(2)设不等式(x﹣a)[x﹣(2﹣a)]<0的解集为N,若N M,求a的取值范围.
【考点】集合的包含关系判断及应用;特称命题.
【分析】(1)若方程m=x2﹣x在[﹣1,1]上有解,即m的取值范围为函数y=x2﹣x在[﹣1,1]上的值域,结合二次函数的图象和性质,要得M;
(2)对a的取值进行分类讨论,求出不等式(x﹣a)[x﹣(2﹣a)]<0的解集为N,结合N M,可得a的取值范围.
【解答】解:(1)由题意知,方程m=x2﹣x在[﹣1,1]上有解,
即m的取值范围为函数y=x2﹣x在[﹣1,1]上的值域,
由函数y=x2﹣x的图象是开口朝上,且以直线x=为对称轴的抛物线,
故当x=时,函数最小值为﹣,当x=﹣1时,函数最大值为2,
故m=[﹣,2],
(2)当a=1时,解集N为空集,满足题意;
当a>1时,a>2﹣a,此时集合N={x|2﹣a<x<a},则1<a≤2
当a<1时,a<2﹣a,此时集合N={x|a<x<2﹣a},则0≤a<1
综上:0≤a≤2
17.已知二次函数f(x)有两个零点0和﹣2,且f(x)最小值是﹣1,函数g(x)与f(x)的图象关于原点对称.
(1)求f(x)和g(x)的解析式;
(2)若h(x)=f(x)﹣λg(x)在区间[﹣1,1]上是增函数,求实数λ的取值范围.
【考点】函数的零点;函数解析式的求解及常用方法;函数单调性的判断与证明.
【分析】(1)根据二次函数的零点,利用待定系数法即可求f(x)和g(x)的解析式;
(2)根据h(x)=f(x)﹣λg(x)在区间[﹣1,1]上是增函数,确定对称轴和对应区间之间的关系,即可求实数λ的取值范围.
【解答】解:(1)∵二次函数f(x)有两个零点0和﹣2,
∴设f(x)=ax(x+2)=ax2+2ax(a>0).f(x)图象的对称轴是x=﹣1,
∴f(﹣1)=﹣1,即a﹣2a=﹣1,
∴a=1,
∴f(x)=x2+2x.
∵函数g(x)的图象与f(x)的图象关于原点对称,
∴g(x)=﹣f(﹣x)=﹣x2+2x.
(2)由(1)得h(x)=x2+2x﹣λ(﹣x2+2x)=(λ+1)x2+2(1﹣λ)x.
①当λ=﹣1时,h(x)=4x满足在区间[﹣1,1]上是增函数;
②当λ<﹣1时,h(x)图象对称轴是x=
则≥1,
又λ<﹣1,解得λ<﹣1;
③当λ>﹣1时,同理需≤﹣1,
又λ>﹣1,解得﹣1<λ≤0.
综上,满足条件的实数λ的取值范围是(﹣∞,0].
18.某市近郊有一块大约500m×500m的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
(1)分别用x表示y和S的函数关系式,并给出定义域;
(2)怎样设计能使S取得最大值,并求出最大值.
【考点】函数模型的选择与应用.
【分析】(1)总面积为xy=3000,且2a+6=y,则y=,(其中6<x<500),从而运动场占地面积为S=(x﹣4)a+(x﹣6)a,代入整理即得;
(2)由(1)知,占地面积S=3030﹣6x﹣=3030﹣(6x+),由基本不等式可得函数的最大值,以及对应的x的值.
【解答】解:(1)由已知xy=3000,∴,其定义域是(6,500).
S=(x﹣4)a+(x﹣6)a=(2x﹣10)a,
∵2a+6=y,∴,
∴,其定义域是(6,500).
(2),
当且仅当,即x=50∈(6,500)时,上述不等式等号成立,
此时,x=50,y=60,Smax=2430.
答:设计x=50m,y=60m时,运动场地面积最大,最大值为2430平方米.
19.已知函数f(x)=|x﹣m|和函数g(x)=x|x﹣m|+m2﹣7m.
(1)若方程f(x)=|m|在[﹣4,+∞)上有两个不同的解,求实数m的取值范围;
(2)若对任意x1∈(﹣∞,4],均存在x2∈[3,+∞),使得f(x1)>g(x2)成立,求实数m的取值范围.
【考点】带绝对值的函数;函数的最值及其几何意义;根的存在性及根的个数判断.
【分析】(1)解方程f(x)=|m|,解得x=0,或x=2m.由题意可得
2m≥﹣4,且2m≠0,由此求得实数m的取值范围.
(2)命题等价于任意x1∈(﹣∞,4],任意的x2∈[3,+∞),fmin(x1)>gmin(x2)
成立,分m<3、
3≤m<4、4≤m三种情况,分别求出实数m的取值范围再取并集,即得所求.
【解答】解:(1)方程f(x)=|m|,即|x﹣m|=|m|,解得x=0,或x=2m.
要使方程|x﹣m|=|m|在[﹣4,+∞)上有两个不同的解,
需
2m≥﹣4,且2m≠0.解得
m≥﹣2
且m≠0.
故实数m的取值范围为[﹣2,0)∪(0,+∞).
(2)由于对任意x1∈(﹣∞,4],都存在x2∈[3,+∞),使f(x1)>g(x2)成立,
故有
fmin(x1)>gmin(x2)
成立.
又函数f(x)=|x﹣m|=,故fmin(x1)=.
又函数g(x)=x|x﹣m|+m2﹣7m=,
故gmin(x2)=.
当m<3时,有0>m2﹣10m+9,解得
1<m<3.
当
3≤m<4,有0>m2﹣7m,解得
3≤m<4.
当4≤m,有m﹣4>m2﹣7m,解得
4≤m<4+2.
综上可得,1<m<4+2,故实数m的取值范围为(1,4+2
).
20.对于函数f(x),若存在实数对(a,b),使得等式f(a+x) f(a﹣x)=b对定义域中的每一个x都成立,则称函数f(x)是“(a,b)型函数”.
(1)判断函数f(x)=4x是否为“(a,b)型函数”,并说明理由;
(2)已知函数g(x)是“(1,4)型函数”,且当x∈[0,1]时,g(x)=x2﹣m(x﹣1)+1(m>0),若当x∈[0,2]时,都有1≤g(x)≤3成立,试求m的取值范围.
【考点】函数与方程的综合运用;抽象函数及其应用.
【分析】(1)利用定义,直接判断求解即可.
(2)由题意得,g(1+x)g(1﹣x)=4,所以当x∈[1,2]时,,其中2﹣x∈[0,1],
而x∈[0,1]时,g(x)=x2+m(1﹣x)+1=x2﹣mx+m+1>0,且其对称轴方程为,通过①当,②当,③当,求出函数的值域,然后推出所求m的取值范围.
【解答】解:(1)函数f(x)=4x是“(a,b)型函数”…
因为由f(a+x) f(a﹣x)=b,得16a=b,所以存在这样的实数对,如a=1,b=16…
(2)由题意得,g(1+x)g(1﹣x)=4,所以当x∈[1,2]时,,其中2﹣x∈[0,1],
而x∈[0,1]时,g(x)=x2+m(1﹣x)+1=x2﹣mx+m+1>0,且其对称轴方程为,
①当,即m>2时,g(x)在[0,1]上的值域为[g(1),g(0)],即[2,m+1],则g(x)在[0,2]上的值域为,由题意得,此时无解…
②当,即1≤m≤2时,g(x)的值域为,即,所以则g(x)在[0,2]上的值域为,则由题意得且,
解得1≤m≤2…
③当,即0<m≤1时,g(x)的值域为,即,则g(x)在[0,2]上的值域为=,
则,解得.
综上所述,所求m的取值范围是…
2016年10月15日
同课章节目录
