27.4正多边形和圆 测试卷(解析版)
文档属性
| 名称 | 27.4正多边形和圆 测试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 559.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-15 21:47:45 | ||
图片预览



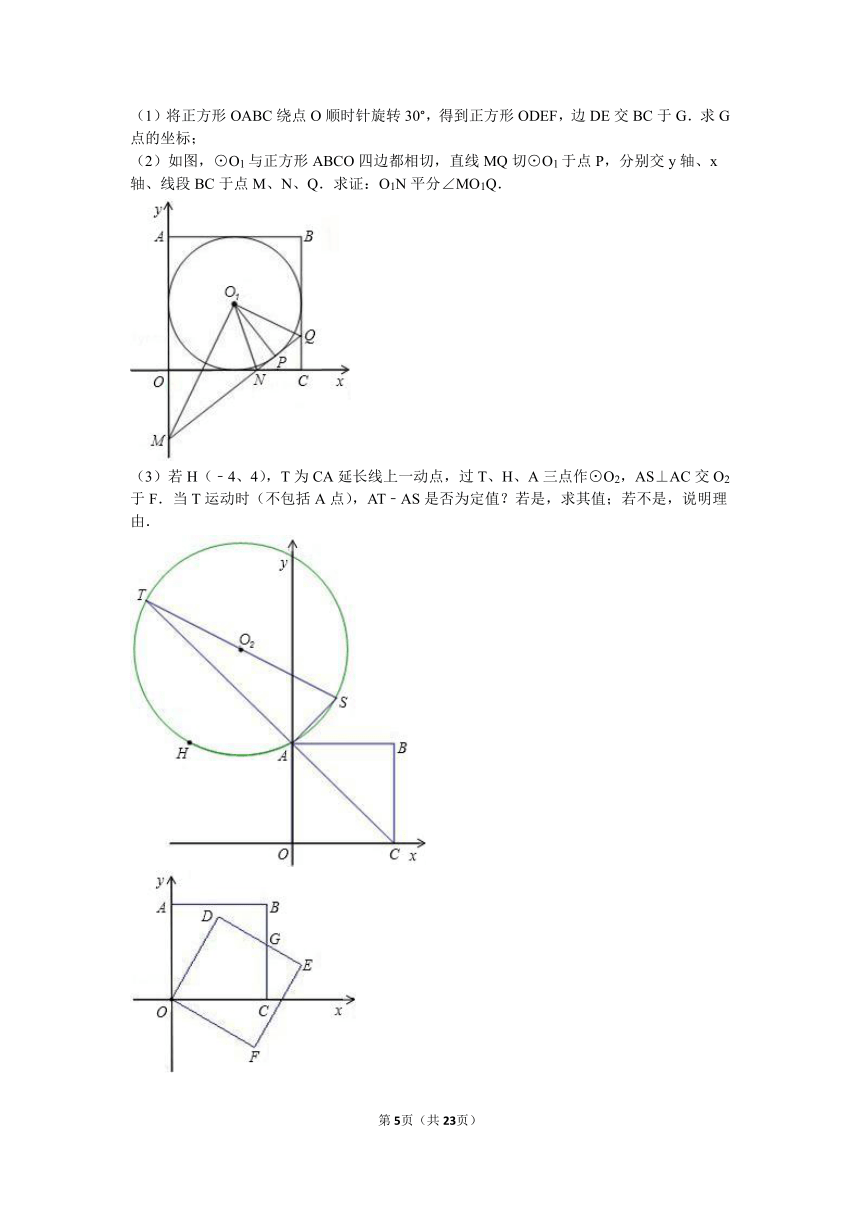
文档简介
华师大版九年级数学下册27.4 正多边形和圆 测试卷
一.选择题(共10小题)
1.正六边形的边心距是,则它的边长是( )
A. B.2 C. D.
2.连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )
A.△ACF是等边三角形
B.连接BF,则BF分别平分∠AFC和∠ABC
C.整个图形是轴对称图形,但不是中心对称图形
D.四边形AFGH与四边形CFED的面积相等
3.用一枚直径为25mm的硬币完全覆盖一个正六边形,则这个正六边形的最大边长是( )
A.mm B.mm C.mm D.mm
4.如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是( )
A.5 B.6 C.7 D.8
5.如图,AB是半径为R的⊙O内接正n边形的边长,则阴影部分的面积为( )
A.﹣R2sin B.﹣R2sin
C.﹣R2sin D.﹣R2sin
6.已知⊙O的半径为r,其内接正六边形,正四边形,正三角形的边长分别为a,b,c,则a:b:c的值为( )
A.1:2:3 B.3:2:1 C.1:: D.::1
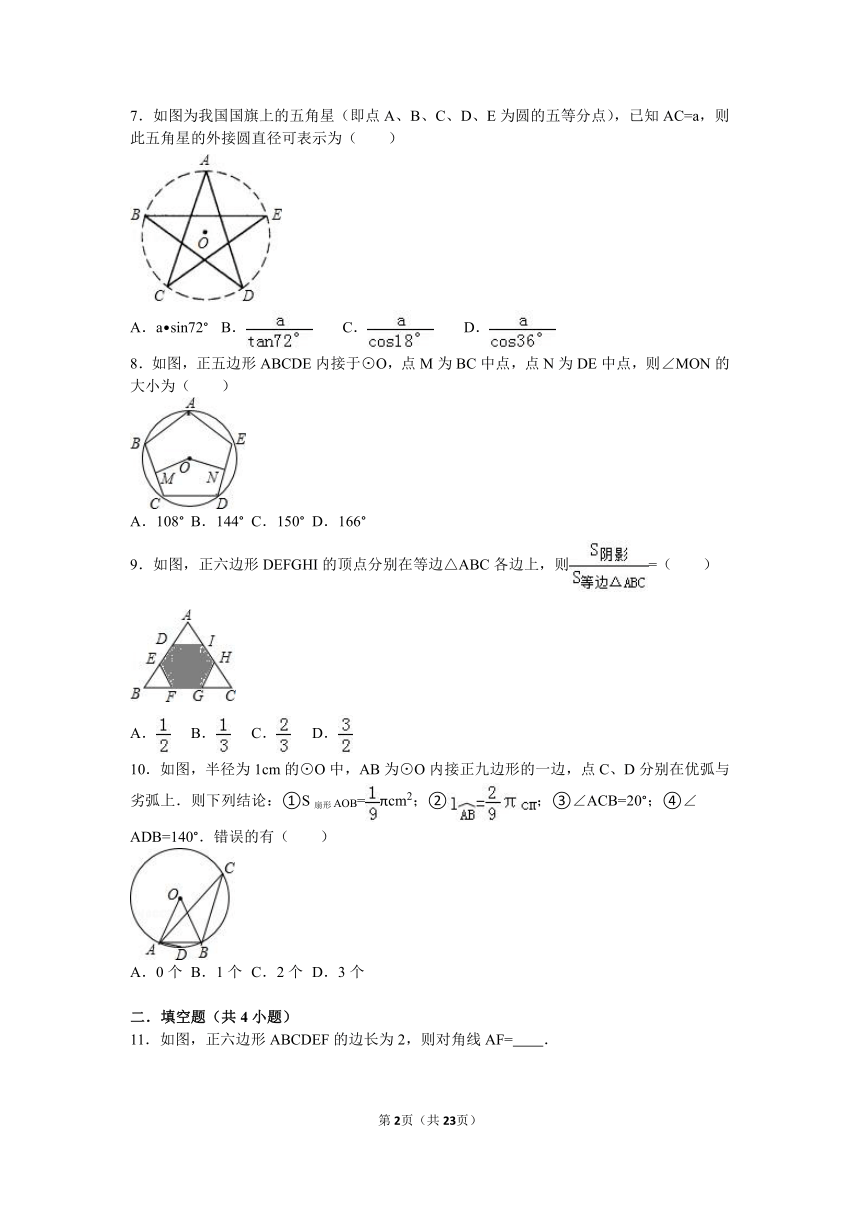
7.如图为我国国旗上的五角星(即点A、B、C、D、E为圆的五等分点),已知AC=a,则此五角星的外接圆直径可表示为( )
A.a?sin72° B. C. D.
8.如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON的大小为( )
A.108° B.144° C.150° D.166°
9.如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则=( )
A. B. C. D.
10.如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB=πcm2;②;③∠ACB=20°;④∠ADB=140°.错误的有( )
A.0个 B.1个 C.2个 D.3个
二.填空题(共4小题)
11.如图,正六边形ABCDEF的边长为2,则对角线AF= .
12.如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为3,则阴影部分的面积为 (结果保留π).
13.如图,等边三角形ABC内接于半径为1的⊙O,以BC为一边作⊙O的内接矩形BCDE,则矩形BCDE的面积为 .
14.半径为4的正n边形边心距为2,则此正n边形的边数为 .
三.解答题(共6小题)
15.如图,以正六边形ABCDEF的边AB为边,在形内作正方形ABMN,连接MC.求∠BCM的大小.
16.如图,O是正六边形ABCDEF的中心,连接BD、DF、FB,
(1)设△BDF的面积为S1,正六边形ABCDEF的面积为S2,则S1与S2的数量关系是 ;
(2)△ABF通过旋转可与△CBD重合,请指出旋转中心和最小旋转角的度数.
17.如图,等腰直角△ABC和等边△AEF都是半径为R的圆的内接三角形.
(1)求AF的长;
(2)通过对△ABC和△AEF的观察,请你先猜想谁的面积大,再证明你的猜想.
18.(1)如图1,已知△PAC是圆O的内接正三角形,那么∠OAC﹦ ;
(2)如图2,设AB是圆O的直径,AC是圆的任意一条弦,∠OAC﹦α﹒
①如果α﹦45°,那么AC能否成为圆内接正多边形的一条边?若有可能,那么此多边形是几边形?请说明理由﹒
②若AC是圆的内接正n边形的一边,则用含n的代数式表示α应为 ﹒
19.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值.
20.在直角坐标系中,正方形OABC的两边OC、OA分别在x轴、y轴上,A点的坐标为(0、4).
(1)将正方形OABC绕点O顺时针旋转30°,得到正方形ODEF,边DE交BC于G.求G点的坐标;
(2)如图,⊙O1与正方形ABCO四边都相切,直线MQ切⊙O1于点P,分别交y轴、x轴、线段BC于点M、N、Q.求证:O1N平分∠MO1Q.
(3)若H(﹣4、4),T为CA延长线上一动点,过T、H、A三点作⊙O2,AS⊥AC交O2于F.当T运动时(不包括A点),AT﹣AS是否为定值?若是,求其值;若不是,说明理由.
参考答案与试题解析
一.选择题(共10小题)
1.(2016?东丽区二模)正六边形的边心距是,则它的边长是( )
A. B.2 C. D.
【分析】运用正六边形的性质,正六边形边长等于外接圆的半径,再利用勾股定理解决.
【解答】解:∵正六边形的边心距为,
∴OB=,AB=OA,
∵OA2=AB2+OB2,
∴OA2=(OA)2+()2,
解得:OA=2.
故选B.
【点评】本题考查了正六边形和圆,掌握外接圆的半径等于正六边形的边长是解此题的关键.
2.(2016?石家庄二模)连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )
A.△ACF是等边三角形
B.连接BF,则BF分别平分∠AFC和∠ABC
C.整个图形是轴对称图形,但不是中心对称图形
D.四边形AFGH与四边形CFED的面积相等
【分析】由正八边形的性质得出A不正确,B、C、D正确,即可得出结论.
【解答】解:∵八边形ABCDEFGH是正八边形,
∴AB=CB=AH=GH=GF=EF=DE=CD,AF=CF,∠AFC=90°﹣45°=45°,
∴∠FAC=∠FCA=(180°﹣45°)=67.5°,
∴△ACF不是等边三角形,选项A错误;
∵正八边形是轴对称图形,直线BF是对称轴,
∴连接BF,则BF分别平分∠AFC和∠ABC,
∴选项B、C正确;
∵四边形AFGH与四边形CFED的面积相等,
∴选项D正确;
故选:A.
【点评】本题考查了正八边形的性质、等腰三角形的性质;熟记正八边形的性质是解决问题的关键.
3.(2016?贵阳模拟)用一枚直径为25mm的硬币完全覆盖一个正六边形,则这个正六边形的最大边长是( )
A.mm B.mm C.mm D.mm
【分析】根据题意得出圆内接半径r为mm,求出OB,得出BD=OB?sin30°,则BC=2BD,即可得出结果.
【解答】解:根据题意得:圆内接半径r为mm,如图所示:
则OB=,
∴BD=OB?sin30°=×=(mm),
则BC=2×=(cm),
完全覆盖住的正六边形的边长最大为mm.
故选:A.
【点评】本题考查了正多边形和圆、正六边形的性质、三角函数、等腰三角形的性质等知识;运用三角函数求出圆内接正六边形的边长是解决问题的关键.
4.(2016?高邮市三模)如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是( )
A.5 B.6 C.7 D.8
【分析】首先求得正五边形的每一个内角的度数,即可求得其对的圆心角度数,继而求得答案.
【解答】解:如图,圆心角为∠1,
∵∵五边形的内角和为:(5﹣2)×180°=3×180°=540°,
∴五边形的每一个内角为:540°÷5=108°,
∴∠1=108°×2﹣180°=216°﹣180°=36°,
∵360°÷36°=10,
∵360°÷36°=10,
∴他要完成这一圆环共需10个全等的五边形.
∴要完全拼成一个圆环还需要的正五边形个数是:10﹣3=7.
故选C.
【点评】此题考查了正多边形与圆的知识.注意求得圆心角的度数是关键.
5.(2016?阜阳校级一模)如图,AB是半径为R的⊙O内接正n边形的边长,则阴影部分的面积为( )
A.﹣R2sin B.﹣R2sin
C.﹣R2sin D.﹣R2sin
【分析】首先连接OA,OB,过点O作OC⊥AB于点C,由AB是半径为R的⊙O内接正n边形的边长,利用三角形函数的性质,可求得△OAB的面积,继而求得扇形OAB的面积,即可求得答案.
【解答】解:连接OA,OB,过点O作OC⊥AB于点C,
则∠AOB=,
∴∠AOC=∠AOB=,
∴OC=OA?cos∠AOC=R?cos,AC=OC?sin∠AOC=R?sin,
∴AB=2AC=2Rsin,
∴S△OAB=AB?OC=×R?cos×2Rsin=R2sin,
∵S扇形OAB=,
∴S阴影=﹣R2sin.
故选A.
【点评】此题考查了正多边形与圆的知识以及三角函数等知识.注意准确作出辅助线是解此题的关键.
6.(2016?兰州模拟)已知⊙O的半径为r,其内接正六边形,正四边形,正三角形的边长分别为a,b,c,则a:b:c的值为( )
A.1:2:3 B.3:2:1 C.1:: D.::1
【分析】根据题意画出图形,再由正多边形的性质及直角三角形的性质求解即可.
【解答】解:如图1所示,
在正三角形ABC中,连接OB,过O作OD⊥BC于D,
则∠OBC=30°,BD=OB?cos30°=r,
故a=BC=2BD=r;
如图2所示,
在正方形ABCD中,连接OB、OC,过O作OE⊥BC于E,
则△OBE是等腰直角三角形,
2BE2=OB2,即BE=r,
故b=BC=r;
如图3所示,
在正六边形ABCDEF中,连接OA、OB,过O作OG⊥AB,则△OAB是等边三角形,
故AG=OA?cos60°=r,
c=AB=2AG=r,
∴圆内接正三角形、正方形、正六边形的边长之比r:r:r=::1.
故选:C.
【点评】本题考查的是圆内接正三角形、正方形及正六边形的性质;根据题意画出图形,作出辅助线构造出直角三角形是解答此题的关键.
7.(2016?萧山区二模)如图为我国国旗上的五角星(即点A、B、C、D、E为圆的五等分点),已知AC=a,则此五角星的外接圆直径可表示为( )
A.a?sin72° B. C. D.
【分析】连AO,并延长交圆O于点F,连接CF.根据直径所对的圆周角是直角,得到直角三角形ACF.根据锐角三角函数进行求解.
【解答】解:连AO,并延长交圆O于点F,连接CF,
则∠ACF=90°;
∵A,B,C,D,E是圆O的五等分点.
∴∠CAD=∠DBE=∠ACE=∠ADB=∠BEC,
又∠CAD+∠DBE+∠ACE+∠ADB+∠BEC=180°,
∴∠CAD=×180°=36°,
∴∠CAF=∠CAD=18°,
在Rt△ACF中,AC=a,
∴AF=;
故选:C.
【点评】本题考查了了圆周角定理的推论和正五边形的性质.熟练运用锐角三角函数进行求解是解决问题的关键.
8.(2016?江东区一模)如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON的大小为( )
A.108° B.144° C.150° D.166°
【分析】由垂径定理得出∠OMC=∠OND=90°,由正五边形的性质得出∠C=∠D=108°,由五边形内角和即可求出结果.
【解答】解:∵点M为BC中点,点N为DE中点,
∴OM⊥BC,ON⊥DE,
∴∠OMC=∠OND=90°,
∵五边形ABCDE是正五边形,
∴∠C=∠D=(5﹣2)×180°÷5=108°,
∴∠MON=(5﹣2)×180°﹣2×90°﹣2×108°=144°;
故选:B.
【点评】本题考查了正五边形的性质、垂径定理;熟练掌握正五边形的性质,由垂径定理得出∠OMC=∠OND=90°是解决问题的关键.
9.(2016?乐亭县一模)如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则=( )
A. B. C. D.
【分析】根据正六边形的每一个内角是120°得到△ADI是等边三角形,得到=,根据相似三角形的性质得到S△ADI=S△ABC,计算即可.
【解答】解:∵六边形DEFGHI是正六边形,
∴∠EDI=120°,
∴∠ADI=60°,
∴△ADI是等边三角形,
∴AD=DE,
同理,BE=DE,
∴AD=DE=EB,
∴=,
∴S△ADI=S△ABC,
同理S△BEF=S△ABC,S△CGH=S△ABC,
∴=,
故选:C.
【点评】本题考查的是正多边形和圆,掌握正多边形的概念和性质以及相似三角形的面积比等于相似比的平方是解题的关键.
10.(2016?海曙区一模)如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB=πcm2;②;③∠ACB=20°;④∠ADB=140°.错误的有( )
A.0个 B.1个 C.2个 D.3个
【分析】由正九边形的性质求出中心角的度数,再由扇形面积公式和弧长公式、圆周角定理以及圆内接四边形的性质即可得出①②③正确,④错误,即可得出结果.
【解答】解:∵AB为⊙O内接正九边形的一边,
∴∠AOB==40°,
∴S扇形AOB==π(cm2),的长==π(cm);∠ACB=∠AOB=20°;
∴①②③正确;∠ADB=180°﹣20°=160°;
∴④错误;错误的有1个,
故选:B.
【点评】本题考查了正九边形的性质、扇形面积公式和弧长公式、圆周角定理以及圆内接四边形的性质;求出正九边形的性质是解决问题的关键.
二.填空题(共4小题)
11.(2016?姜堰区校级模拟)如图,正六边形ABCDEF的边长为2,则对角线AF= 2 .
【分析】作BG⊥AF,垂足为G.构造等腰三角形ABF,在直角三角形ABG中,求出AG的长,即可得出AF.
【解答】解:作BG⊥AF,垂足为G.如图所示:
∵AB=BF=2,
∴AG=FG,
∵∠ABF=120°,
∴∠BAF=30°,
∴AG=AB?cos30°=2×=,
∴AC=2AG=2;
故答案为2.
【点评】本题考查了正多边形和圆、正六边形的性质、等腰三角形的性质、三角函数;熟练掌握正六边形的性质,由三角函数求出AG是解决问题的关键.
12.(2016?长春模拟)如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为3,则阴影部分的面积为 3π (结果保留π).
【分析】首先连接OC,OE,分别交BD,DF于点M,N,易证得S△OBM=S△DCM,同理:S△OFN=S△DEN,则可得S阴影=S扇形OCE.
【解答】解:连接OC,OE,分别交BD,DF于点M,N,
∵正六边形ABCDEF内接于⊙O,
∴∠BOC=60°,∠BCD=∠COE=120°,
∵OB=OC,
∴△OBC是等边三角形,
∴∠OBC=∠OCB=60°,
∴∠OCD=∠OCB,
∵BC=CD,
∴∠CBD=∠CDM=30°,BM=DM,
∴∠OBM=30°,S△DCM=S△BCM,
∴∠OBM=∠CBD,
∴OM=CM,
∴S△OBM=S△BCM,
∴S△OBM=S△DCM,
同理:S△OFN=S△DEN,
∴S阴影=S扇形OCE==3π.
故答案为:3π.
【点评】此题考查了正多边形与圆的知识以及扇形的面积公式.注意证得S阴影=S扇形OCE是关键.
13.(2016?江西模拟)如图,等边三角形ABC内接于半径为1的⊙O,以BC为一边作⊙O的内接矩形BCDE,则矩形BCDE的面积为 .
【分析】连接BD,由等边三角形的性质和圆周角定理得出∠BDC=∠BAC=60°,由矩形的性质和圆周角定理证出BD是⊙O的直径,得出BD=2,CD=BD=1,由勾股定理得出=,即可求出矩形BCDE的面积.
【解答】解:连接BD,如图所示:
∵△ABC是等边三角形,
∴∠BAC=60°,
∴∠BDC=∠BAC=60°,
∵四边形BCDE是矩形,
∴∠BCD=90°,
∴BD是⊙O的直径,∠CBD=90°﹣60°=30°,
∴BD=2,CD=BD=1,
∴BC==,
∴矩形BCDE的面积=BC?CD=×1=;
故答案为:.
【点评】本题考查了正多边形和圆、等边三角形的性质、含30°角的直角三角形的性质、勾股定理、圆周角定理等知识;熟练掌握等边三角形的性质,由圆周角定理证出BD是直径是解决问题的关键.
14.(2016?南江县校级模拟)半径为4的正n边形边心距为2,则此正n边形的边数为 6 .
【分析】由三角函数求出∠DAO=60°,得出∠AOD=30°,求出中心角∠AOB=60°,即可得出答案.
【解答】解:如图所示AB为正n边形的边长,OA为半径,OD为边心距,
∵半径为4的正n边形边心距为2,
∴sin∠DAO===,
∴∠DAO=60°,
∴∠AOD=30°,
∴∠AOB=60°,
∴n==6.
故答案为:6.
【点评】此题主要考查了正多边形和圆的有关计算,根据已知得出中心角∠AOB=60°是解题关键.
三.解答题(共6小题)
15.(2012?长春模拟)如图,以正六边形ABCDEF的边AB为边,在形内作正方形ABMN,连接MC.求∠BCM的大小.
【分析】△BCM是等腰三角形,只要求出顶角∠CBM就可以,这个角是正六边形与正方形内角的差.
【解答】解:∵六边形ABCDEF为正六边形,
∴∠ABC=120°,AB=BC.
∵四边形ABMN为正方形,
∴∠ABM=90°,AB=BM.(2分)
∴∠MBC=120°﹣90°=30°,BM=BC.
∴∠BCM=∠BMC.
∴∠BCM=×(180°﹣30°)=75°.(5分)
【点评】本题就是一个求正多边形的内角的问题,注意到△BCM是等腰三角形是解决本题的关键.
16.(2012?安徽模拟)如图,O是正六边形ABCDEF的中心,连接BD、DF、FB,
(1)设△BDF的面积为S1,正六边形ABCDEF的面积为S2,则S1与S2的数量关系是 S2=2S1 ;
(2)△ABF通过旋转可与△CBD重合,请指出旋转中心和最小旋转角的度数.
【分析】(1)先连接OD、OF、OB,根据正六边形、正三角形的性质可知△ABF、△BDC、△DEF、△DOF、△BOF、△BOD都是全等的,易求S2=2S1;
(2)由于正n边形关于对称中心O旋转与自身重合,易求旋转角度.
【解答】解:(1)S2=2S1,如右图所示,连接OD、OF、OB,
∵六边形ABCDEF是正六边形,
∴△BDF是正三角形,
∴△ABF、△BDC、△DEF、△DOF、△BOF、△BOD都是全等的,
∴S2=2S1;
(2)旋转中心是O,最小旋转角是120°,
由于正n边形关于对称中心O旋转与自身重合,而通过观察可知△ABF必须逆时针旋转才可以与△CBD重合,
故旋转的角度==120°.
【点评】本题考查了正多边形的定义、性质和旋转的性质.正三边形的中心与顶点的连线构成的3个三角形全等,正n边形关于对称中心O旋转与自身重合.
17.(2012?安徽模拟)如图,等腰直角△ABC和等边△AEF都是半径为R的圆的内接三角形.
(1)求AF的长;
(2)通过对△ABC和△AEF的观察,请你先猜想谁的面积大,再证明你的猜想.
【分析】(1)连接OF,过O作OG⊥AF于G,在直角△OGF中,利用三角函数即可求解;
(2)根据外接圆的半径是R,即可求得等腰直角△ABC和等边△AEF的面积,即可作出比较.
【解答】解:(1)连接OF,过O作OG⊥AF于G,OF=R,
又∵△AEF为等边三角形,
∴∠AOF=120°,
∴∠GOF=60°,
∴GF=R,则AF=R
(2)S△ABC<S△AEF,
∵直角△ABC是等腰直角三角形.
∴AB=2R,
∴AC=R,
∴S△ABC=R2
,,
∴S△ABC<S△AEF
【点评】本题主要考查了正多边形与圆的计算,正确理解等腰直角三角形的斜边就是外接圆的直径,正多边形的计算可以转化为直角三角形的计算.
18.(2011?婺城区模拟)(1)如图1,已知△PAC是圆O的内接正三角形,那么∠OAC﹦ 30° ;
(2)如图2,设AB是圆O的直径,AC是圆的任意一条弦,∠OAC﹦α﹒
①如果α﹦45°,那么AC能否成为圆内接正多边形的一条边?若有可能,那么此多边形是几边形?请说明理由﹒
②若AC是圆的内接正n边形的一边,则用含n的代数式表示α应为 90°﹣ ﹒
【分析】(1)先根据圆周角定理求出∠AOC的度数,再根据三角形内角和定理及等腰三角形的性质即可解答;
(2)①假设AC是圆内接多边形的一条边,则此多边形的内角为45°×2=90°,故此多边形是正方形;
②根据正多边形内角和定理即可求出答案.
【解答】解:(1)∵△PAC是圆O的内接正三角形,
∴∠AOC=2∠APC=2×60°=120°,
∵OA=OC,
∴∠OAC===30°;
(2)①能﹒
∵α=45°,
∴圆内接正多边形的一个内角为90°,
∴是正方形﹒
②∵AC是圆的内接正n边形的一边,
∴2α=,
∴α=90°﹣.
【点评】本题考查的是正多边形和圆,涉及到的知识点为:圆周角定理、正多边形的性质及内角和定理,难度适中.
19.(2015秋?连云港期中)如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值.
【分析】(1)连接BD,根据圆的内接四边形的性质得出∠BAD的度数,由AB=AD,可证得△ABD是等边三角形,求得∠ABD=60°,再利用圆的内接四边形的性质,即可求得∠E的度数;
(2)连接OA,由圆周角定理求出∠AOD的度数,由弧长公式即可得出的长;
(3)首先连接OA,由∠ABD=60°,利用圆周角定理,即可求得∠AOD的度数,继而求得∠AOE的度数,即可得出结果.
【解答】解:(1)连接BD,如图1所示:
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠C=180°,
∵∠C=120°,
∴∠BAD=60°,
∵AB=AD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∵四边形ABDE是⊙O的内接四边形,∴∠AED+∠ABD=180°,
∴∠AED=120°;
(2)∵∠AOD=2∠ABD=120°,
∴的长==;
(3)连接OA,如图2所示:
∵∠ABD=60°,
∴∠AOD=2∠ABD=120°,
∵∠DOE=90°,
∴∠AOE=∠AOD﹣∠DOE=30°,
∴n==12.
【点评】此题考查了圆的内接四边形的性质、圆周角定理以及等边三角形的判定与性质.注意准确作出辅助线是解此题的关键.
20.(2012秋?东湖区期中)在直角坐标系中,正方形OABC的两边OC、OA分别在x轴、y轴上,A点的坐标为(0、4).
(1)将正方形OABC绕点O顺时针旋转30°,得到正方形ODEF,边DE交BC于G.求G点的坐标;
(2)如图,⊙O1与正方形ABCO四边都相切,直线MQ切⊙O1于点P,分别交y轴、x轴、线段BC于点M、N、Q.求证:O1N平分∠MO1Q.
(3)若H(﹣4、4),T为CA延长线上一动点,过T、H、A三点作⊙O2,AS⊥AC交O2于F.当T运动时(不包括A点),AT﹣AS是否为定值?若是,求其值;若不是,说明理由.
【分析】(1)求出旋转角∠AOD、∠FOC的度数为30°,进而求出∠GOC的度数,再利用三角函数求出G点坐标;
(2)由切线长定理证得∠MO1Q=90°,由切线长定理或其他方法证得∠NO1Q=45°,O1N平分∠MO1Q;
(3)在AT上取点V,使TV=AS,构造出全等三角形△HTV≌△HSA,判断出△HAV为等腰直角三角形,
求得AT﹣AS=AV=为定值.
【解答】解:(1)连接OG,
∵∠AOD=∠FOC=30°,由轴对称可得∠DOG=∠COG=30°,
又∴OC=4,
∵CG=OC?tan∠COG=4×=,(2分)
∴G(4,);(3分)
(2)∵BQ∥AM,
∴∠BQM+∠AMQ=180°,
根据切线长定理,∠O1QM+∠Q1MQ=180°×=90°,
∴∠MO1Q=180°﹣90°=90°,(5分)
由切线长定理∠NO1Q=45°,
∴O1N平分∠MO1Q.(7分)
(3)AQ﹣AF的值是定值为4,(8分)
在AT上取点V,使TV=AS,即AT﹣AS=AV,
∵AS⊥AC,
∴∠THS=∠TAS=90°,
∵H(﹣4、4),A(0、4),
∴AH⊥AO;
又∵∠OAC=45°,
∴∠TAH=45°,(9分)
∵∠THS=∠TAS=90°,
∴∠TSH=45°,
∴HT=HS;
又∠HTV=∠HAS,TV=AS,
∴△HTV≌△HSA,(11分)
∴△HAV为等腰直角三角形,
∴AT﹣AS=AV=,AH=4.(12分)
【点评】(1)此题不仅要熟悉旋转角,还要知道旋转不变性,并联系特殊三角形用勾股定理解答;
(2)运用切割线定理是解答此题的关键;
(3)构造全等三角形,比作辅助线难度要大,但确是一种有效的解题方法.
一.选择题(共10小题)
1.正六边形的边心距是,则它的边长是( )
A. B.2 C. D.
2.连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )
A.△ACF是等边三角形
B.连接BF,则BF分别平分∠AFC和∠ABC
C.整个图形是轴对称图形,但不是中心对称图形
D.四边形AFGH与四边形CFED的面积相等
3.用一枚直径为25mm的硬币完全覆盖一个正六边形,则这个正六边形的最大边长是( )
A.mm B.mm C.mm D.mm
4.如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是( )
A.5 B.6 C.7 D.8
5.如图,AB是半径为R的⊙O内接正n边形的边长,则阴影部分的面积为( )
A.﹣R2sin B.﹣R2sin
C.﹣R2sin D.﹣R2sin
6.已知⊙O的半径为r,其内接正六边形,正四边形,正三角形的边长分别为a,b,c,则a:b:c的值为( )
A.1:2:3 B.3:2:1 C.1:: D.::1
7.如图为我国国旗上的五角星(即点A、B、C、D、E为圆的五等分点),已知AC=a,则此五角星的外接圆直径可表示为( )
A.a?sin72° B. C. D.
8.如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON的大小为( )
A.108° B.144° C.150° D.166°
9.如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则=( )
A. B. C. D.
10.如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB=πcm2;②;③∠ACB=20°;④∠ADB=140°.错误的有( )
A.0个 B.1个 C.2个 D.3个
二.填空题(共4小题)
11.如图,正六边形ABCDEF的边长为2,则对角线AF= .
12.如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为3,则阴影部分的面积为 (结果保留π).
13.如图,等边三角形ABC内接于半径为1的⊙O,以BC为一边作⊙O的内接矩形BCDE,则矩形BCDE的面积为 .
14.半径为4的正n边形边心距为2,则此正n边形的边数为 .
三.解答题(共6小题)
15.如图,以正六边形ABCDEF的边AB为边,在形内作正方形ABMN,连接MC.求∠BCM的大小.
16.如图,O是正六边形ABCDEF的中心,连接BD、DF、FB,
(1)设△BDF的面积为S1,正六边形ABCDEF的面积为S2,则S1与S2的数量关系是 ;
(2)△ABF通过旋转可与△CBD重合,请指出旋转中心和最小旋转角的度数.
17.如图,等腰直角△ABC和等边△AEF都是半径为R的圆的内接三角形.
(1)求AF的长;
(2)通过对△ABC和△AEF的观察,请你先猜想谁的面积大,再证明你的猜想.
18.(1)如图1,已知△PAC是圆O的内接正三角形,那么∠OAC﹦ ;
(2)如图2,设AB是圆O的直径,AC是圆的任意一条弦,∠OAC﹦α﹒
①如果α﹦45°,那么AC能否成为圆内接正多边形的一条边?若有可能,那么此多边形是几边形?请说明理由﹒
②若AC是圆的内接正n边形的一边,则用含n的代数式表示α应为 ﹒
19.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值.
20.在直角坐标系中,正方形OABC的两边OC、OA分别在x轴、y轴上,A点的坐标为(0、4).
(1)将正方形OABC绕点O顺时针旋转30°,得到正方形ODEF,边DE交BC于G.求G点的坐标;
(2)如图,⊙O1与正方形ABCO四边都相切,直线MQ切⊙O1于点P,分别交y轴、x轴、线段BC于点M、N、Q.求证:O1N平分∠MO1Q.
(3)若H(﹣4、4),T为CA延长线上一动点,过T、H、A三点作⊙O2,AS⊥AC交O2于F.当T运动时(不包括A点),AT﹣AS是否为定值?若是,求其值;若不是,说明理由.
参考答案与试题解析
一.选择题(共10小题)
1.(2016?东丽区二模)正六边形的边心距是,则它的边长是( )
A. B.2 C. D.
【分析】运用正六边形的性质,正六边形边长等于外接圆的半径,再利用勾股定理解决.
【解答】解:∵正六边形的边心距为,
∴OB=,AB=OA,
∵OA2=AB2+OB2,
∴OA2=(OA)2+()2,
解得:OA=2.
故选B.
【点评】本题考查了正六边形和圆,掌握外接圆的半径等于正六边形的边长是解此题的关键.
2.(2016?石家庄二模)连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )
A.△ACF是等边三角形
B.连接BF,则BF分别平分∠AFC和∠ABC
C.整个图形是轴对称图形,但不是中心对称图形
D.四边形AFGH与四边形CFED的面积相等
【分析】由正八边形的性质得出A不正确,B、C、D正确,即可得出结论.
【解答】解:∵八边形ABCDEFGH是正八边形,
∴AB=CB=AH=GH=GF=EF=DE=CD,AF=CF,∠AFC=90°﹣45°=45°,
∴∠FAC=∠FCA=(180°﹣45°)=67.5°,
∴△ACF不是等边三角形,选项A错误;
∵正八边形是轴对称图形,直线BF是对称轴,
∴连接BF,则BF分别平分∠AFC和∠ABC,
∴选项B、C正确;
∵四边形AFGH与四边形CFED的面积相等,
∴选项D正确;
故选:A.
【点评】本题考查了正八边形的性质、等腰三角形的性质;熟记正八边形的性质是解决问题的关键.
3.(2016?贵阳模拟)用一枚直径为25mm的硬币完全覆盖一个正六边形,则这个正六边形的最大边长是( )
A.mm B.mm C.mm D.mm
【分析】根据题意得出圆内接半径r为mm,求出OB,得出BD=OB?sin30°,则BC=2BD,即可得出结果.
【解答】解:根据题意得:圆内接半径r为mm,如图所示:
则OB=,
∴BD=OB?sin30°=×=(mm),
则BC=2×=(cm),
完全覆盖住的正六边形的边长最大为mm.
故选:A.
【点评】本题考查了正多边形和圆、正六边形的性质、三角函数、等腰三角形的性质等知识;运用三角函数求出圆内接正六边形的边长是解决问题的关键.
4.(2016?高邮市三模)如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是( )
A.5 B.6 C.7 D.8
【分析】首先求得正五边形的每一个内角的度数,即可求得其对的圆心角度数,继而求得答案.
【解答】解:如图,圆心角为∠1,
∵∵五边形的内角和为:(5﹣2)×180°=3×180°=540°,
∴五边形的每一个内角为:540°÷5=108°,
∴∠1=108°×2﹣180°=216°﹣180°=36°,
∵360°÷36°=10,
∵360°÷36°=10,
∴他要完成这一圆环共需10个全等的五边形.
∴要完全拼成一个圆环还需要的正五边形个数是:10﹣3=7.
故选C.
【点评】此题考查了正多边形与圆的知识.注意求得圆心角的度数是关键.
5.(2016?阜阳校级一模)如图,AB是半径为R的⊙O内接正n边形的边长,则阴影部分的面积为( )
A.﹣R2sin B.﹣R2sin
C.﹣R2sin D.﹣R2sin
【分析】首先连接OA,OB,过点O作OC⊥AB于点C,由AB是半径为R的⊙O内接正n边形的边长,利用三角形函数的性质,可求得△OAB的面积,继而求得扇形OAB的面积,即可求得答案.
【解答】解:连接OA,OB,过点O作OC⊥AB于点C,
则∠AOB=,
∴∠AOC=∠AOB=,
∴OC=OA?cos∠AOC=R?cos,AC=OC?sin∠AOC=R?sin,
∴AB=2AC=2Rsin,
∴S△OAB=AB?OC=×R?cos×2Rsin=R2sin,
∵S扇形OAB=,
∴S阴影=﹣R2sin.
故选A.
【点评】此题考查了正多边形与圆的知识以及三角函数等知识.注意准确作出辅助线是解此题的关键.
6.(2016?兰州模拟)已知⊙O的半径为r,其内接正六边形,正四边形,正三角形的边长分别为a,b,c,则a:b:c的值为( )
A.1:2:3 B.3:2:1 C.1:: D.::1
【分析】根据题意画出图形,再由正多边形的性质及直角三角形的性质求解即可.
【解答】解:如图1所示,
在正三角形ABC中,连接OB,过O作OD⊥BC于D,
则∠OBC=30°,BD=OB?cos30°=r,
故a=BC=2BD=r;
如图2所示,
在正方形ABCD中,连接OB、OC,过O作OE⊥BC于E,
则△OBE是等腰直角三角形,
2BE2=OB2,即BE=r,
故b=BC=r;
如图3所示,
在正六边形ABCDEF中,连接OA、OB,过O作OG⊥AB,则△OAB是等边三角形,
故AG=OA?cos60°=r,
c=AB=2AG=r,
∴圆内接正三角形、正方形、正六边形的边长之比r:r:r=::1.
故选:C.
【点评】本题考查的是圆内接正三角形、正方形及正六边形的性质;根据题意画出图形,作出辅助线构造出直角三角形是解答此题的关键.
7.(2016?萧山区二模)如图为我国国旗上的五角星(即点A、B、C、D、E为圆的五等分点),已知AC=a,则此五角星的外接圆直径可表示为( )
A.a?sin72° B. C. D.
【分析】连AO,并延长交圆O于点F,连接CF.根据直径所对的圆周角是直角,得到直角三角形ACF.根据锐角三角函数进行求解.
【解答】解:连AO,并延长交圆O于点F,连接CF,
则∠ACF=90°;
∵A,B,C,D,E是圆O的五等分点.
∴∠CAD=∠DBE=∠ACE=∠ADB=∠BEC,
又∠CAD+∠DBE+∠ACE+∠ADB+∠BEC=180°,
∴∠CAD=×180°=36°,
∴∠CAF=∠CAD=18°,
在Rt△ACF中,AC=a,
∴AF=;
故选:C.
【点评】本题考查了了圆周角定理的推论和正五边形的性质.熟练运用锐角三角函数进行求解是解决问题的关键.
8.(2016?江东区一模)如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON的大小为( )
A.108° B.144° C.150° D.166°
【分析】由垂径定理得出∠OMC=∠OND=90°,由正五边形的性质得出∠C=∠D=108°,由五边形内角和即可求出结果.
【解答】解:∵点M为BC中点,点N为DE中点,
∴OM⊥BC,ON⊥DE,
∴∠OMC=∠OND=90°,
∵五边形ABCDE是正五边形,
∴∠C=∠D=(5﹣2)×180°÷5=108°,
∴∠MON=(5﹣2)×180°﹣2×90°﹣2×108°=144°;
故选:B.
【点评】本题考查了正五边形的性质、垂径定理;熟练掌握正五边形的性质,由垂径定理得出∠OMC=∠OND=90°是解决问题的关键.
9.(2016?乐亭县一模)如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则=( )
A. B. C. D.
【分析】根据正六边形的每一个内角是120°得到△ADI是等边三角形,得到=,根据相似三角形的性质得到S△ADI=S△ABC,计算即可.
【解答】解:∵六边形DEFGHI是正六边形,
∴∠EDI=120°,
∴∠ADI=60°,
∴△ADI是等边三角形,
∴AD=DE,
同理,BE=DE,
∴AD=DE=EB,
∴=,
∴S△ADI=S△ABC,
同理S△BEF=S△ABC,S△CGH=S△ABC,
∴=,
故选:C.
【点评】本题考查的是正多边形和圆,掌握正多边形的概念和性质以及相似三角形的面积比等于相似比的平方是解题的关键.
10.(2016?海曙区一模)如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB=πcm2;②;③∠ACB=20°;④∠ADB=140°.错误的有( )
A.0个 B.1个 C.2个 D.3个
【分析】由正九边形的性质求出中心角的度数,再由扇形面积公式和弧长公式、圆周角定理以及圆内接四边形的性质即可得出①②③正确,④错误,即可得出结果.
【解答】解:∵AB为⊙O内接正九边形的一边,
∴∠AOB==40°,
∴S扇形AOB==π(cm2),的长==π(cm);∠ACB=∠AOB=20°;
∴①②③正确;∠ADB=180°﹣20°=160°;
∴④错误;错误的有1个,
故选:B.
【点评】本题考查了正九边形的性质、扇形面积公式和弧长公式、圆周角定理以及圆内接四边形的性质;求出正九边形的性质是解决问题的关键.
二.填空题(共4小题)
11.(2016?姜堰区校级模拟)如图,正六边形ABCDEF的边长为2,则对角线AF= 2 .
【分析】作BG⊥AF,垂足为G.构造等腰三角形ABF,在直角三角形ABG中,求出AG的长,即可得出AF.
【解答】解:作BG⊥AF,垂足为G.如图所示:
∵AB=BF=2,
∴AG=FG,
∵∠ABF=120°,
∴∠BAF=30°,
∴AG=AB?cos30°=2×=,
∴AC=2AG=2;
故答案为2.
【点评】本题考查了正多边形和圆、正六边形的性质、等腰三角形的性质、三角函数;熟练掌握正六边形的性质,由三角函数求出AG是解决问题的关键.
12.(2016?长春模拟)如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为3,则阴影部分的面积为 3π (结果保留π).
【分析】首先连接OC,OE,分别交BD,DF于点M,N,易证得S△OBM=S△DCM,同理:S△OFN=S△DEN,则可得S阴影=S扇形OCE.
【解答】解:连接OC,OE,分别交BD,DF于点M,N,
∵正六边形ABCDEF内接于⊙O,
∴∠BOC=60°,∠BCD=∠COE=120°,
∵OB=OC,
∴△OBC是等边三角形,
∴∠OBC=∠OCB=60°,
∴∠OCD=∠OCB,
∵BC=CD,
∴∠CBD=∠CDM=30°,BM=DM,
∴∠OBM=30°,S△DCM=S△BCM,
∴∠OBM=∠CBD,
∴OM=CM,
∴S△OBM=S△BCM,
∴S△OBM=S△DCM,
同理:S△OFN=S△DEN,
∴S阴影=S扇形OCE==3π.
故答案为:3π.
【点评】此题考查了正多边形与圆的知识以及扇形的面积公式.注意证得S阴影=S扇形OCE是关键.
13.(2016?江西模拟)如图,等边三角形ABC内接于半径为1的⊙O,以BC为一边作⊙O的内接矩形BCDE,则矩形BCDE的面积为 .
【分析】连接BD,由等边三角形的性质和圆周角定理得出∠BDC=∠BAC=60°,由矩形的性质和圆周角定理证出BD是⊙O的直径,得出BD=2,CD=BD=1,由勾股定理得出=,即可求出矩形BCDE的面积.
【解答】解:连接BD,如图所示:
∵△ABC是等边三角形,
∴∠BAC=60°,
∴∠BDC=∠BAC=60°,
∵四边形BCDE是矩形,
∴∠BCD=90°,
∴BD是⊙O的直径,∠CBD=90°﹣60°=30°,
∴BD=2,CD=BD=1,
∴BC==,
∴矩形BCDE的面积=BC?CD=×1=;
故答案为:.
【点评】本题考查了正多边形和圆、等边三角形的性质、含30°角的直角三角形的性质、勾股定理、圆周角定理等知识;熟练掌握等边三角形的性质,由圆周角定理证出BD是直径是解决问题的关键.
14.(2016?南江县校级模拟)半径为4的正n边形边心距为2,则此正n边形的边数为 6 .
【分析】由三角函数求出∠DAO=60°,得出∠AOD=30°,求出中心角∠AOB=60°,即可得出答案.
【解答】解:如图所示AB为正n边形的边长,OA为半径,OD为边心距,
∵半径为4的正n边形边心距为2,
∴sin∠DAO===,
∴∠DAO=60°,
∴∠AOD=30°,
∴∠AOB=60°,
∴n==6.
故答案为:6.
【点评】此题主要考查了正多边形和圆的有关计算,根据已知得出中心角∠AOB=60°是解题关键.
三.解答题(共6小题)
15.(2012?长春模拟)如图,以正六边形ABCDEF的边AB为边,在形内作正方形ABMN,连接MC.求∠BCM的大小.
【分析】△BCM是等腰三角形,只要求出顶角∠CBM就可以,这个角是正六边形与正方形内角的差.
【解答】解:∵六边形ABCDEF为正六边形,
∴∠ABC=120°,AB=BC.
∵四边形ABMN为正方形,
∴∠ABM=90°,AB=BM.(2分)
∴∠MBC=120°﹣90°=30°,BM=BC.
∴∠BCM=∠BMC.
∴∠BCM=×(180°﹣30°)=75°.(5分)
【点评】本题就是一个求正多边形的内角的问题,注意到△BCM是等腰三角形是解决本题的关键.
16.(2012?安徽模拟)如图,O是正六边形ABCDEF的中心,连接BD、DF、FB,
(1)设△BDF的面积为S1,正六边形ABCDEF的面积为S2,则S1与S2的数量关系是 S2=2S1 ;
(2)△ABF通过旋转可与△CBD重合,请指出旋转中心和最小旋转角的度数.
【分析】(1)先连接OD、OF、OB,根据正六边形、正三角形的性质可知△ABF、△BDC、△DEF、△DOF、△BOF、△BOD都是全等的,易求S2=2S1;
(2)由于正n边形关于对称中心O旋转与自身重合,易求旋转角度.
【解答】解:(1)S2=2S1,如右图所示,连接OD、OF、OB,
∵六边形ABCDEF是正六边形,
∴△BDF是正三角形,
∴△ABF、△BDC、△DEF、△DOF、△BOF、△BOD都是全等的,
∴S2=2S1;
(2)旋转中心是O,最小旋转角是120°,
由于正n边形关于对称中心O旋转与自身重合,而通过观察可知△ABF必须逆时针旋转才可以与△CBD重合,
故旋转的角度==120°.
【点评】本题考查了正多边形的定义、性质和旋转的性质.正三边形的中心与顶点的连线构成的3个三角形全等,正n边形关于对称中心O旋转与自身重合.
17.(2012?安徽模拟)如图,等腰直角△ABC和等边△AEF都是半径为R的圆的内接三角形.
(1)求AF的长;
(2)通过对△ABC和△AEF的观察,请你先猜想谁的面积大,再证明你的猜想.
【分析】(1)连接OF,过O作OG⊥AF于G,在直角△OGF中,利用三角函数即可求解;
(2)根据外接圆的半径是R,即可求得等腰直角△ABC和等边△AEF的面积,即可作出比较.
【解答】解:(1)连接OF,过O作OG⊥AF于G,OF=R,
又∵△AEF为等边三角形,
∴∠AOF=120°,
∴∠GOF=60°,
∴GF=R,则AF=R
(2)S△ABC<S△AEF,
∵直角△ABC是等腰直角三角形.
∴AB=2R,
∴AC=R,
∴S△ABC=R2
,,
∴S△ABC<S△AEF
【点评】本题主要考查了正多边形与圆的计算,正确理解等腰直角三角形的斜边就是外接圆的直径,正多边形的计算可以转化为直角三角形的计算.
18.(2011?婺城区模拟)(1)如图1,已知△PAC是圆O的内接正三角形,那么∠OAC﹦ 30° ;
(2)如图2,设AB是圆O的直径,AC是圆的任意一条弦,∠OAC﹦α﹒
①如果α﹦45°,那么AC能否成为圆内接正多边形的一条边?若有可能,那么此多边形是几边形?请说明理由﹒
②若AC是圆的内接正n边形的一边,则用含n的代数式表示α应为 90°﹣ ﹒
【分析】(1)先根据圆周角定理求出∠AOC的度数,再根据三角形内角和定理及等腰三角形的性质即可解答;
(2)①假设AC是圆内接多边形的一条边,则此多边形的内角为45°×2=90°,故此多边形是正方形;
②根据正多边形内角和定理即可求出答案.
【解答】解:(1)∵△PAC是圆O的内接正三角形,
∴∠AOC=2∠APC=2×60°=120°,
∵OA=OC,
∴∠OAC===30°;
(2)①能﹒
∵α=45°,
∴圆内接正多边形的一个内角为90°,
∴是正方形﹒
②∵AC是圆的内接正n边形的一边,
∴2α=,
∴α=90°﹣.
【点评】本题考查的是正多边形和圆,涉及到的知识点为:圆周角定理、正多边形的性质及内角和定理,难度适中.
19.(2015秋?连云港期中)如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值.
【分析】(1)连接BD,根据圆的内接四边形的性质得出∠BAD的度数,由AB=AD,可证得△ABD是等边三角形,求得∠ABD=60°,再利用圆的内接四边形的性质,即可求得∠E的度数;
(2)连接OA,由圆周角定理求出∠AOD的度数,由弧长公式即可得出的长;
(3)首先连接OA,由∠ABD=60°,利用圆周角定理,即可求得∠AOD的度数,继而求得∠AOE的度数,即可得出结果.
【解答】解:(1)连接BD,如图1所示:
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠C=180°,
∵∠C=120°,
∴∠BAD=60°,
∵AB=AD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∵四边形ABDE是⊙O的内接四边形,∴∠AED+∠ABD=180°,
∴∠AED=120°;
(2)∵∠AOD=2∠ABD=120°,
∴的长==;
(3)连接OA,如图2所示:
∵∠ABD=60°,
∴∠AOD=2∠ABD=120°,
∵∠DOE=90°,
∴∠AOE=∠AOD﹣∠DOE=30°,
∴n==12.
【点评】此题考查了圆的内接四边形的性质、圆周角定理以及等边三角形的判定与性质.注意准确作出辅助线是解此题的关键.
20.(2012秋?东湖区期中)在直角坐标系中,正方形OABC的两边OC、OA分别在x轴、y轴上,A点的坐标为(0、4).
(1)将正方形OABC绕点O顺时针旋转30°,得到正方形ODEF,边DE交BC于G.求G点的坐标;
(2)如图,⊙O1与正方形ABCO四边都相切,直线MQ切⊙O1于点P,分别交y轴、x轴、线段BC于点M、N、Q.求证:O1N平分∠MO1Q.
(3)若H(﹣4、4),T为CA延长线上一动点,过T、H、A三点作⊙O2,AS⊥AC交O2于F.当T运动时(不包括A点),AT﹣AS是否为定值?若是,求其值;若不是,说明理由.
【分析】(1)求出旋转角∠AOD、∠FOC的度数为30°,进而求出∠GOC的度数,再利用三角函数求出G点坐标;
(2)由切线长定理证得∠MO1Q=90°,由切线长定理或其他方法证得∠NO1Q=45°,O1N平分∠MO1Q;
(3)在AT上取点V,使TV=AS,构造出全等三角形△HTV≌△HSA,判断出△HAV为等腰直角三角形,
求得AT﹣AS=AV=为定值.
【解答】解:(1)连接OG,
∵∠AOD=∠FOC=30°,由轴对称可得∠DOG=∠COG=30°,
又∴OC=4,
∵CG=OC?tan∠COG=4×=,(2分)
∴G(4,);(3分)
(2)∵BQ∥AM,
∴∠BQM+∠AMQ=180°,
根据切线长定理,∠O1QM+∠Q1MQ=180°×=90°,
∴∠MO1Q=180°﹣90°=90°,(5分)
由切线长定理∠NO1Q=45°,
∴O1N平分∠MO1Q.(7分)
(3)AQ﹣AF的值是定值为4,(8分)
在AT上取点V,使TV=AS,即AT﹣AS=AV,
∵AS⊥AC,
∴∠THS=∠TAS=90°,
∵H(﹣4、4),A(0、4),
∴AH⊥AO;
又∵∠OAC=45°,
∴∠TAH=45°,(9分)
∵∠THS=∠TAS=90°,
∴∠TSH=45°,
∴HT=HS;
又∠HTV=∠HAS,TV=AS,
∴△HTV≌△HSA,(11分)
∴△HAV为等腰直角三角形,
∴AT﹣AS=AV=,AH=4.(12分)
【点评】(1)此题不仅要熟悉旋转角,还要知道旋转不变性,并联系特殊三角形用勾股定理解答;
(2)运用切割线定理是解答此题的关键;
(3)构造全等三角形,比作辅助线难度要大,但确是一种有效的解题方法.
