华师大版八年级数学下册20.1.1平均数的意义测试卷(解析版)
文档属性
| 名称 | 华师大版八年级数学下册20.1.1平均数的意义测试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 66.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-15 00:00:00 | ||
图片预览




文档简介
华师大版八年级数学下册20.1.1 平均数的意义 测试卷
一.选择题(共10小题)
1.已知一组数据1,7,10,8,x,6,0,3,若,则x应等于( )
A.6 B.5 C.4 D.2
2.已知a,b,c,d,e的平均分是,则a+5,b+12,c+22,d+9,e+2的平均分是( )
A.﹣1 B.+3 C.+10 D.+12
3.将20个数据各减去30后,得到的一组新数据的平均数是6,则这20个数据的平均数是( )
A.35 B.36 C.37 D.38
4.小华所在的九年级一班共有50名学生,一次体检测量了全班学生的身高,由此求得该班学生的平均身高为1.65米,而小华的身高为1.66米.下列说法错误的是( )
A.1.65米是该班学生身高的平均水平
B.班上比小华高的学生不会超过25人
C.这组身高的中位数不一定是1.65米
D.这组身高的众数不一定是1.65米
5.在演讲比赛中,5为评委给一位歌手打分如下:8.2分、8.3分、7.8分、7.7分、8.0分,则这位歌手平均得分( )
A.7.8 B.8.0 C.8.2 D.8.3
6.我市欲从某师范院校招聘一名“特岗教师”,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:
候选人
甲
乙
丙
丁
测试成绩
面试
86
91
90
83
笔试
90
83
83
92
根据录用程序,作为人们教师面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权.根据四人各自的平均成绩,你认为将录取( )
A.甲 B.乙 C.丙 D.丁
7.某中学规定学生的学期体育成绩满分100分,其中课外体育占20%,其中考试成绩占30%,期末考试成绩占50%.小彤的三项成绩(百分制)依次为95,90,94,则小彤这学期的体育成绩为( )
A.89 B.90 C.92 D.93
8.小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分、80分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )
A.255分 B.84分 C.84.5分 D.86分
9.学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )
A.2 B.2.8 C.3 D.3.3
10.某年级有四个班,人数分别为:一班25人,二班22人,三班27人,四班26人.在一次考试中,四个班的班级平均分依次为81分,75分,89分,78分,则这次考试的年级平均分为( )
A.79.25分 B.80.75分 C.81.06分 D.82.53分
二.填空题(共4小题)
11.设有四个数,其中每三个数的和分别为24,36,28,32.则这四个数的平均数为 .
12.若李老师六个月的手机上网流量(单位:M)分别为526,600,874,480,620,500,则李老师这六个月平均每个月的手机上网流量为 M.
13.如图显示是某班20人在“献爱心”活动中捐图书的情况,该班人均捐了 册.
14.小王某学期的物理成绩分别为:平时平均成绩得84分,期中考试得90分,期末考试得85 分.若按如图所显示的权重,那么小王该学期的总评成绩应该为 分.
三.解答题(共6小题)
15.有一组数据:3,x2+1,5,2x﹣3,4,它们的平均数是4,求x的值.
16.某学校设立学生奖学金时规定:综合成绩最高者得一等奖,综合成绩包括体育成绩、德育成绩、学习成绩三项,这三项成绩分别按1:3:6的比例计入综合成绩.小明、小亮两位同学入围测评,他们的体育成绩、德育成绩、学习成绩如下表.请你通过计算他们的综合成绩,判断谁能拿到一等奖?
体育成绩
德育成绩
学习成绩
小明
96
94
90
小亮
90
93
92
17.将若干由1开始的连续自然数写在纸上,然后删去其中一个数,则余下的数的平均数为53,问删去的那个数是多少?
18.一组数据a,1.8,2.2,1.8,b的平均数是1.96,求a,b两数的平均数.
19.东升广告公司欲招聘广告策划人员一名,对甲、乙、丙三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
测试项目
测 试 成 绩
甲
乙
丙
创 新
72
85
67
综合知识
50
74
70
语 言
88
45
67
(1)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用?
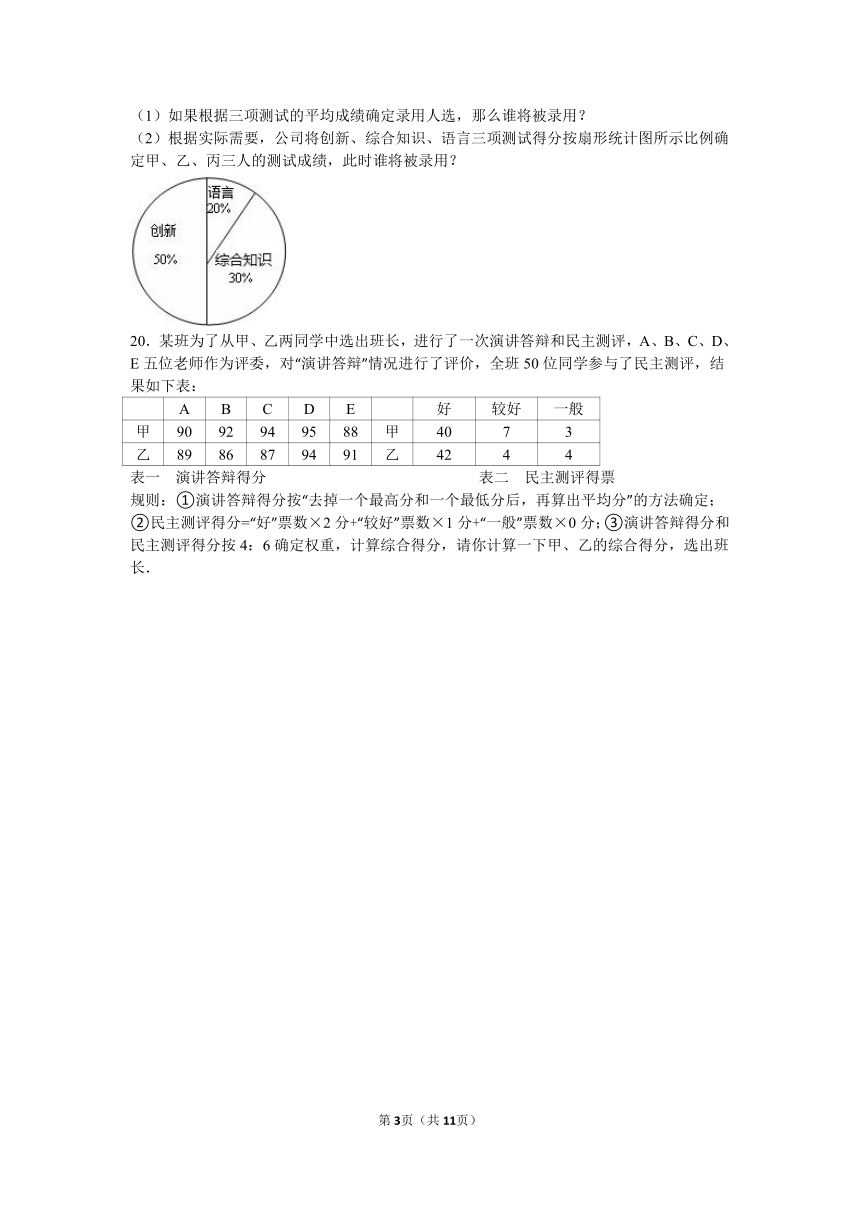
(2)根据实际需要,公司将创新、综合知识、语言三项测试得分按扇形统计图所示比例确定甲、乙、丙三人的测试成绩,此时谁将被录用?
20.某班为了从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评,A、B、C、D、E五位老师作为评委,对“演讲答辩”情况进行了评价,全班50位同学参与了民主测评,结果如下表:
A
B
C
D
E
好
较好
一般
甲
90
92
94
95
88
甲
40
7
3
乙
89
86
87
94
91
乙
42
4
4
表一 演讲答辩得分 表二 民主测评得票
规则:①演讲答辩得分按“去掉一个最高分和一个最低分后,再算出平均分”的方法确定;②民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;③演讲答辩得分和民主测评得分按4:6确定权重,计算综合得分,请你计算一下甲、乙的综合得分,选出班长.
参考答案与试题解析
一.选择题(共10小题)
1.(2015?呼和浩特一模)已知一组数据1,7,10,8,x,6,0,3,若,则x应等于( )
A.6 B.5 C.4 D.2
【分析】本题需先根据已知条件和算术平均数的定义列出式子,解出得数即可求出答案.
【解答】解:(1+7+10+8+x+6+0+3)÷8=5
35+x=40,
x=5.
故选B.
【点评】本题主要考查了算术平均数,在解题时要根据已知条件列出式子解出得数是本题的关键.
2.(2015?清远模拟)已知a,b,c,d,e的平均分是,则a+5,b+12,c+22,d+9,e+2的平均分是( )
A.﹣1 B.+3 C.+10 D.+12
【分析】首先求出a+5,b+12,c+22,d+9,e+2总分,进而得出平均分即可.
【解答】解:∵a,b,c,d,e的平均分是,
∴a+5+b+12+c+22+d+9+e+2=5+50,
∴则a+5,b+12,c+22,d+9,e+2的平均分是:(5+50)÷5=+10.
故选:C.
【点评】此题主要考查了算术平均数的求法,利用已知得出这5个数的总分是解题关键.
3.(2015?恩施州一模)将20个数据各减去30后,得到的一组新数据的平均数是6,则这20个数据的平均数是( )
A.35 B.36 C.37 D.38
【分析】根据平均数的定义和计算公式即可得出答案.
【解答】解:将20个数据分别减去30后平均数为6,则原数据的平均数为6+30=36.
故选B.
【点评】本题考查了平均数的概念,平均数是指在一组数据中所有数据之和再除以数据的个数.
4.(2015?婺城区模拟)小华所在的九年级一班共有50名学生,一次体检测量了全班学生的身高,由此求得该班学生的平均身高为1.65米,而小华的身高为1.66米.下列说法错误的是( )
A.1.65米是该班学生身高的平均水平
B.班上比小华高的学生不会超过25人
C.这组身高的中位数不一定是1.65米
D.这组身高的众数不一定是1.65米
【分析】A:根据算术平均数的含义,可得1.65米是该班学生身高的平均水平,据此判断即可.
B:根据小华所在的九年级一班共有50名学生,可得班上比小华高的学生可能超过25人,据此判断即可.
C:根据中位数的含义,可得这组身高的中位数不一定是1.65米,据此判断即可.
D:根据众数的含义,可得这组身高的众数不一定是1.65米,据此判断即可.
【解答】解:∵该班学生的平均身高为1.65米,
∴1.65米是该班学生身高的平均水平,
∴选项A正确;
∵小华所在的九年级一班共有50名学生,
∴班上比小华高的学生可能超过25人,
∴选项B不正确;
∵这组身高的中位数不一定是1.65米,
∴选项C正确;
∵这组身高的众数不一定是1.65米,
∴选项D正确.
故选:B.
【点评】此题主要考查了算术平均数的含义和求法,要熟练掌握,解答此题的关键是要明确:(1)平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.(2)算术平均数:对于n个数x1,x2,…,xn,则xˉ=1n(x1+x2+…+xn)就叫做这n个数的算术平均数.(3)算术平均数是加权平均数的一种特殊情况,加权平均数包含算术平均数,当加权平均数中的权相等时,就是算术平均数.
5.(2015春?莒县期末)在演讲比赛中,5为评委给一位歌手打分如下:8.2分、8.3分、7.8分、7.7分、8.0分,则这位歌手平均得分( )
A.7.8 B.8.0 C.8.2 D.8.3
【分析】根据算术平均数的计算公式,先求出这5个数的和,再除以5即可.
【解答】解:根据题意得:
(8.2+8.3+7.8+7.7+8.0)÷5=8(分)
故选(B)
【点评】此题主要考查了算术平均数,用到的知识点是算术平均数的计算公式,熟记公式是解决本题的关键.
6.(2016?宛城区一模)我市欲从某师范院校招聘一名“特岗教师”,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:
候选人
甲
乙
丙
丁
测试成绩
面试
86
91
90
83
笔试
90
83
83
92
根据录用程序,作为人们教师面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权.根据四人各自的平均成绩,你认为将录取( )
A.甲 B.乙 C.丙 D.丁
【分析】根据加权平均数的公式分别求出甲、乙、丙、丁四人的平均成绩,做比较后即可得出结论.
【解答】解:甲的平均成绩为:×(86×6+90×4)=87.6(分),
乙的平均成绩为:×(91×6+83×4)=87.8(分),
丙的平均成绩为:×(90×6+83×4)=87.2(分),
丁的平均成绩为:×(83×6+92×4)=86.4(分),
∵87.8>87.6>87.2>86.4,
∴乙的平均成绩最高.
故选B.
【点评】本题考查了加权平均数,解题的关键是能够熟练的运用加权平均数的公式求一组数据的加权平均数.本题属于基础题,难度不大,牢牢掌握加权平均数的公式是关键.
7.(2016春?自贡期末)某中学规定学生的学期体育成绩满分100分,其中课外体育占20%,其中考试成绩占30%,期末考试成绩占50%.小彤的三项成绩(百分制)依次为95,90,94,则小彤这学期的体育成绩为( )
A.89 B.90 C.92 D.93
【分析】根据加权平均数的公式,套入数据即可得出结论.
【解答】解:小彤这学期的体育成绩为=(20×95+30×90+50×94)=93(分).
故选D.
【点评】本题考查了折线统计图以及加权平均数,解题的关键是利用加权平均数的公式求出小彤这学期的体育成绩.本题属于基础题,难度不大,解决该题型题目时,熟记加权平均数的公式是解题的关键.
8.(2015?河南)小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分、80分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )
A.255分 B.84分 C.84.5分 D.86分
【分析】根据题意列出算式,计算即可得到结果.
【解答】解:根据题意得:85×+80×+90×=17+24+45=86(分),
故选D
【点评】此题考查了加权平均数,熟练掌握加权平均数的求法是解本题的关键.
9.(2015?玉林)学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )
A.2 B.2.8 C.3 D.3.3
【分析】平均数的计算方法是求出所有数据的和,然后除以数据的总个数.注意本题不是求3,5,11,11这四个数的平均数.
【解答】解:(3×1+5×2+11×3+11×4)÷30
=(3+10+33+44)÷30
=90÷30
=3.
故30名学生参加活动的平均次数是3.
故选:C.
【点评】本题考查加权平均数,条形统计图和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
10.(2015?河北区二模)某年级有四个班,人数分别为:一班25人,二班22人,三班27人,四班26人.在一次考试中,四个班的班级平均分依次为81分,75分,89分,78分,则这次考试的年级平均分为( )
A.79.25分 B.80.75分 C.81.06分 D.82.53分
【分析】平均数的计算方法是求出所有学生的总分之和,然后除以学生总数.
【解答】解:该组数据的平均数==81.06分;
故选C.
【点评】本题考查的是加权平均数的求法.本题易出现的错误是求81,89,78,75这四个数的平均数,对平均数的理解不正确.
二.填空题(共4小题)
11.(2016?黄冈校级自主招生)设有四个数,其中每三个数的和分别为24,36,28,32.则这四个数的平均数为 10 .
【分析】可以设这四个数分别是a,b,c,d,根据条件就可列方程组,从而根据平均数的计算公式求解.
【解答】解:设这四个数分别是a,b,c,d,
根据题意得:
四个式子相加得:a+b+c+d=40
则平均数是=10
故答案是:10.
【点评】本题主要考查了平均数的计算方法,正确解方程组是解题的关键.
12.(2015?玄武区一模)若李老师六个月的手机上网流量(单位:M)分别为526,600,874,480,620,500,则李老师这六个月平均每个月的手机上网流量为 600 M.
【分析】只要运用求平均数公式:即可求出答案.
【解答】解:根据题意得:
(526+600+874+480+620+500)÷6=600(M);
答:李老师这六个月平均每个月的手机上网流量为600M;
故答案为:600.
【点评】本题考查的是算术平均数的求法.熟记公式是解决本题的关键.
13.(2016春?睢宁县校级月考)如图显示是某班20人在“献爱心”活动中捐图书的情况,该班人均捐了 2.8 册.
【分析】根据条形统计图可算出捐2本书的人数,再利用加权平均数的公式即可算出该班人均捐书本书.
【解答】解:捐2本书的人数为:20﹣2﹣4﹣4﹣2=8(人),
该班人均捐书本数为:×(1×2+2×8+3×4+4×4+5×2)=2.8(本).
故答案为:2.8.
【点评】本题考查了加权平均数以及条形统计图,解题的关键是结合调休统计图求出捐2本书的人数.本题属于基础题,难度不大,解决该题型题目时,能够熟练运用加权平均数公式解决问题是关键.
14.(2015春?防城区期末)小王某学期的物理成绩分别为:平时平均成绩得84分,期中考试得90分,期末考试得85 分.若按如图所显示的权重,那么小王该学期的总评成绩应该为 86.4 分.
【分析】根据加权平均数的计算公式列出算式,再进行计算即可.
【解答】解:根据题意得:
84×10%+90×30%+85×60%=86.4(分),
答:小王该学期的总评成绩应该为86.4分.
故答案为:86.4.
【点评】此题考查了加权平均数,本题易出现的错误是求84,90,85的平均数,对加权平均数的理解不正确.
三.解答题(共6小题)
15.(2014春?萧山区校级月考)有一组数据:3,x2+1,5,2x﹣3,4,它们的平均数是4,求x的值.
【分析】由平均数的定义可得x的方程,解方程可得.
【解答】解:由题意可得3+x2+1+5+2x﹣3+4=4×5,
整理,得x2+2x﹣10=0,
解得x1=﹣1+,x2=﹣1﹣.
即所求x的值为﹣1+或﹣1﹣.
【点评】本题考查平均数的定义,平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.本题是基础题.
16.(2016春?洛江区期末)某学校设立学生奖学金时规定:综合成绩最高者得一等奖,综合成绩包括体育成绩、德育成绩、学习成绩三项,这三项成绩分别按1:3:6的比例计入综合成绩.小明、小亮两位同学入围测评,他们的体育成绩、德育成绩、学习成绩如下表.请你通过计算他们的综合成绩,判断谁能拿到一等奖?
体育成绩
德育成绩
学习成绩
小明
96
94
90
小亮
90
93
92
【分析】根据加权平均数的定义分别计算两人的加权平均数,然后比较大小即可.
【解答】解:小明的综合成绩=0.1×96+0.3×94+0.6×90=91.8,
小亮的综合成绩=0.1×90+0.3×93+0.6×92=92.1,
∵92.1>91.8,
∴小亮能拿到一等奖.
【点评】本题考查了加权平均数:若n个数x1,x2,x3,…,xn的权分别是w1,w2,w3,…,wn,则(x1w1+x2w2+…+xnwn)÷(w1+w2+…+wn)叫做这n个数的加权平均数.
17.将若干由1开始的连续自然数写在纸上,然后删去其中一个数,则余下的数的平均数为53,问删去的那个数是多少?
【分析】基于平均数的考虑:1,2,3,4,…,105的平均数是53,1,2,3,4,…,106的平均数是53.5,它应该有105个或106个连续数,由于减去一个数的平均为53,当n=105个,但104×53不是整数,故否定了有105个数.当106个数时,可以尝试错误法找出.
【解答】解:1,2,3,4,….,105的平均数是53,
1,2,3,4,….,106的平均数是53.5
它应该有105个或106个连续数.
(1)由于减去一个数的平均为53,当n=105个,但104×53不是整数,故否定了有105个数.
(2)当106个数时,很明显不会删去106,故应是1﹣105中其中一个数,考虑平均数的分数部,由于是105个数的平均,故将=,当中表示删去的数为106﹣45=61,或1+2+3+…+106=5671,
当减去一个数后,平均为53,n=105,
和=53×105=5610,
所以减去的一个数应是5671﹣5610=61.
答:删去的那个数是61.
【点评】本题考查的是样本平均数的求法及运用,解题的关键是先确定连续自然数介于105个或106个连续数,然后讨论即可.
18.一组数据a,1.8,2.2,1.8,b的平均数是1.96,求a,b两数的平均数.
【分析】由平均数的公式即可计算出a+b的值,进一步求得a,b两数的平均数即可.
【解答】解:由题意得:
×(1.8+2.2+1.8+a+b)=1.96,
解得a+b=4.
故a,b两数的平均数是4÷2=2.
【点评】本题考查了算术平均数的计算方法,解题的关键是正确的应用公式.
19.(2015春?惠安县期末)东升广告公司欲招聘广告策划人员一名,对甲、乙、丙三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
测试项目
测 试 成 绩
甲
乙
丙
创 新
72
85
67
综合知识
50
74
70
语 言
88
45
67
(1)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用?
(2)根据实际需要,公司将创新、综合知识、语言三项测试得分按扇形统计图所示比例确定甲、乙、丙三人的测试成绩,此时谁将被录用?
【分析】(1)先根据题意求出甲、乙、丙的平均成绩,再进行比较即可;
(2)按扇形统计图所示比例求出甲、乙、丙三人的测试成绩,再进行比较即可.
【解答】解:(1)∵甲三项测试的平均成绩为:(72+50+88)÷3=70,
乙三项测试的平均成绩为(85+74+45)÷3=68,
丙三项测试的平均成绩为(67+70+67)÷3=68;
∴甲将被录用.
(2)分别为:
甲:72×50%+50×30%+88×20%=68.6
乙:85×50%+74×30%+45×20%=73.7
丙:67×50%+70×30%+67×20%=67.9
∴乙将被录用.
【点评】此题考查了加权平均数,关键是根据题意列出算式,求出平均数,用到的知识点是加权平均数的计算公式.
20.(2015秋?滕州市校级期末)某班为了从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评,A、B、C、D、E五位老师作为评委,对“演讲答辩”情况进行了评价,全班50位同学参与了民主测评,结果如下表:
A
B
C
D
E
好
较好
一般
甲
90
92
94
95
88
甲
40
7
3
乙
89
86
87
94
91
乙
42
4
4
表一 演讲答辩得分 表二 民主测评得票
规则:①演讲答辩得分按“去掉一个最高分和一个最低分后,再算出平均分”的方法确定;②民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;③演讲答辩得分和民主测评得分按4:6确定权重,计算综合得分,请你计算一下甲、乙的综合得分,选出班长.
【分析】首先分别求出甲、乙两位选手各自演讲答辩的平均分,然后根据平均数的概念分别计算出甲、乙两位选手的民主测评分,最后根据不同权重计算加权成绩.
【解答】解:甲演讲答辩的平均分为:=92;
乙演讲答辩的平均分为:=89,
甲民主测评分为:40×2+7×1=87,
乙民主测评分为:42×2+4×1=88,
∴甲综合得分:=89,
∴乙综合得分:=88.4,
∵89>88.4,
∴应选择甲当班长.
【点评】本题考查了平均数和加权平均数的概念及应用,以及从表格中获取信息的能力.
一.选择题(共10小题)
1.已知一组数据1,7,10,8,x,6,0,3,若,则x应等于( )
A.6 B.5 C.4 D.2
2.已知a,b,c,d,e的平均分是,则a+5,b+12,c+22,d+9,e+2的平均分是( )
A.﹣1 B.+3 C.+10 D.+12
3.将20个数据各减去30后,得到的一组新数据的平均数是6,则这20个数据的平均数是( )
A.35 B.36 C.37 D.38
4.小华所在的九年级一班共有50名学生,一次体检测量了全班学生的身高,由此求得该班学生的平均身高为1.65米,而小华的身高为1.66米.下列说法错误的是( )
A.1.65米是该班学生身高的平均水平
B.班上比小华高的学生不会超过25人
C.这组身高的中位数不一定是1.65米
D.这组身高的众数不一定是1.65米
5.在演讲比赛中,5为评委给一位歌手打分如下:8.2分、8.3分、7.8分、7.7分、8.0分,则这位歌手平均得分( )
A.7.8 B.8.0 C.8.2 D.8.3
6.我市欲从某师范院校招聘一名“特岗教师”,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:
候选人
甲
乙
丙
丁
测试成绩
面试
86
91
90
83
笔试
90
83
83
92
根据录用程序,作为人们教师面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权.根据四人各自的平均成绩,你认为将录取( )
A.甲 B.乙 C.丙 D.丁
7.某中学规定学生的学期体育成绩满分100分,其中课外体育占20%,其中考试成绩占30%,期末考试成绩占50%.小彤的三项成绩(百分制)依次为95,90,94,则小彤这学期的体育成绩为( )
A.89 B.90 C.92 D.93
8.小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分、80分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )
A.255分 B.84分 C.84.5分 D.86分
9.学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )
A.2 B.2.8 C.3 D.3.3
10.某年级有四个班,人数分别为:一班25人,二班22人,三班27人,四班26人.在一次考试中,四个班的班级平均分依次为81分,75分,89分,78分,则这次考试的年级平均分为( )
A.79.25分 B.80.75分 C.81.06分 D.82.53分
二.填空题(共4小题)
11.设有四个数,其中每三个数的和分别为24,36,28,32.则这四个数的平均数为 .
12.若李老师六个月的手机上网流量(单位:M)分别为526,600,874,480,620,500,则李老师这六个月平均每个月的手机上网流量为 M.
13.如图显示是某班20人在“献爱心”活动中捐图书的情况,该班人均捐了 册.
14.小王某学期的物理成绩分别为:平时平均成绩得84分,期中考试得90分,期末考试得85 分.若按如图所显示的权重,那么小王该学期的总评成绩应该为 分.
三.解答题(共6小题)
15.有一组数据:3,x2+1,5,2x﹣3,4,它们的平均数是4,求x的值.
16.某学校设立学生奖学金时规定:综合成绩最高者得一等奖,综合成绩包括体育成绩、德育成绩、学习成绩三项,这三项成绩分别按1:3:6的比例计入综合成绩.小明、小亮两位同学入围测评,他们的体育成绩、德育成绩、学习成绩如下表.请你通过计算他们的综合成绩,判断谁能拿到一等奖?
体育成绩
德育成绩
学习成绩
小明
96
94
90
小亮
90
93
92
17.将若干由1开始的连续自然数写在纸上,然后删去其中一个数,则余下的数的平均数为53,问删去的那个数是多少?
18.一组数据a,1.8,2.2,1.8,b的平均数是1.96,求a,b两数的平均数.
19.东升广告公司欲招聘广告策划人员一名,对甲、乙、丙三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
测试项目
测 试 成 绩
甲
乙
丙
创 新
72
85
67
综合知识
50
74
70
语 言
88
45
67
(1)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用?
(2)根据实际需要,公司将创新、综合知识、语言三项测试得分按扇形统计图所示比例确定甲、乙、丙三人的测试成绩,此时谁将被录用?
20.某班为了从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评,A、B、C、D、E五位老师作为评委,对“演讲答辩”情况进行了评价,全班50位同学参与了民主测评,结果如下表:
A
B
C
D
E
好
较好
一般
甲
90
92
94
95
88
甲
40
7
3
乙
89
86
87
94
91
乙
42
4
4
表一 演讲答辩得分 表二 民主测评得票
规则:①演讲答辩得分按“去掉一个最高分和一个最低分后,再算出平均分”的方法确定;②民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;③演讲答辩得分和民主测评得分按4:6确定权重,计算综合得分,请你计算一下甲、乙的综合得分,选出班长.
参考答案与试题解析
一.选择题(共10小题)
1.(2015?呼和浩特一模)已知一组数据1,7,10,8,x,6,0,3,若,则x应等于( )
A.6 B.5 C.4 D.2
【分析】本题需先根据已知条件和算术平均数的定义列出式子,解出得数即可求出答案.
【解答】解:(1+7+10+8+x+6+0+3)÷8=5
35+x=40,
x=5.
故选B.
【点评】本题主要考查了算术平均数,在解题时要根据已知条件列出式子解出得数是本题的关键.
2.(2015?清远模拟)已知a,b,c,d,e的平均分是,则a+5,b+12,c+22,d+9,e+2的平均分是( )
A.﹣1 B.+3 C.+10 D.+12
【分析】首先求出a+5,b+12,c+22,d+9,e+2总分,进而得出平均分即可.
【解答】解:∵a,b,c,d,e的平均分是,
∴a+5+b+12+c+22+d+9+e+2=5+50,
∴则a+5,b+12,c+22,d+9,e+2的平均分是:(5+50)÷5=+10.
故选:C.
【点评】此题主要考查了算术平均数的求法,利用已知得出这5个数的总分是解题关键.
3.(2015?恩施州一模)将20个数据各减去30后,得到的一组新数据的平均数是6,则这20个数据的平均数是( )
A.35 B.36 C.37 D.38
【分析】根据平均数的定义和计算公式即可得出答案.
【解答】解:将20个数据分别减去30后平均数为6,则原数据的平均数为6+30=36.
故选B.
【点评】本题考查了平均数的概念,平均数是指在一组数据中所有数据之和再除以数据的个数.
4.(2015?婺城区模拟)小华所在的九年级一班共有50名学生,一次体检测量了全班学生的身高,由此求得该班学生的平均身高为1.65米,而小华的身高为1.66米.下列说法错误的是( )
A.1.65米是该班学生身高的平均水平
B.班上比小华高的学生不会超过25人
C.这组身高的中位数不一定是1.65米
D.这组身高的众数不一定是1.65米
【分析】A:根据算术平均数的含义,可得1.65米是该班学生身高的平均水平,据此判断即可.
B:根据小华所在的九年级一班共有50名学生,可得班上比小华高的学生可能超过25人,据此判断即可.
C:根据中位数的含义,可得这组身高的中位数不一定是1.65米,据此判断即可.
D:根据众数的含义,可得这组身高的众数不一定是1.65米,据此判断即可.
【解答】解:∵该班学生的平均身高为1.65米,
∴1.65米是该班学生身高的平均水平,
∴选项A正确;
∵小华所在的九年级一班共有50名学生,
∴班上比小华高的学生可能超过25人,
∴选项B不正确;
∵这组身高的中位数不一定是1.65米,
∴选项C正确;
∵这组身高的众数不一定是1.65米,
∴选项D正确.
故选:B.
【点评】此题主要考查了算术平均数的含义和求法,要熟练掌握,解答此题的关键是要明确:(1)平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.(2)算术平均数:对于n个数x1,x2,…,xn,则xˉ=1n(x1+x2+…+xn)就叫做这n个数的算术平均数.(3)算术平均数是加权平均数的一种特殊情况,加权平均数包含算术平均数,当加权平均数中的权相等时,就是算术平均数.
5.(2015春?莒县期末)在演讲比赛中,5为评委给一位歌手打分如下:8.2分、8.3分、7.8分、7.7分、8.0分,则这位歌手平均得分( )
A.7.8 B.8.0 C.8.2 D.8.3
【分析】根据算术平均数的计算公式,先求出这5个数的和,再除以5即可.
【解答】解:根据题意得:
(8.2+8.3+7.8+7.7+8.0)÷5=8(分)
故选(B)
【点评】此题主要考查了算术平均数,用到的知识点是算术平均数的计算公式,熟记公式是解决本题的关键.
6.(2016?宛城区一模)我市欲从某师范院校招聘一名“特岗教师”,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:
候选人
甲
乙
丙
丁
测试成绩
面试
86
91
90
83
笔试
90
83
83
92
根据录用程序,作为人们教师面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权.根据四人各自的平均成绩,你认为将录取( )
A.甲 B.乙 C.丙 D.丁
【分析】根据加权平均数的公式分别求出甲、乙、丙、丁四人的平均成绩,做比较后即可得出结论.
【解答】解:甲的平均成绩为:×(86×6+90×4)=87.6(分),
乙的平均成绩为:×(91×6+83×4)=87.8(分),
丙的平均成绩为:×(90×6+83×4)=87.2(分),
丁的平均成绩为:×(83×6+92×4)=86.4(分),
∵87.8>87.6>87.2>86.4,
∴乙的平均成绩最高.
故选B.
【点评】本题考查了加权平均数,解题的关键是能够熟练的运用加权平均数的公式求一组数据的加权平均数.本题属于基础题,难度不大,牢牢掌握加权平均数的公式是关键.
7.(2016春?自贡期末)某中学规定学生的学期体育成绩满分100分,其中课外体育占20%,其中考试成绩占30%,期末考试成绩占50%.小彤的三项成绩(百分制)依次为95,90,94,则小彤这学期的体育成绩为( )
A.89 B.90 C.92 D.93
【分析】根据加权平均数的公式,套入数据即可得出结论.
【解答】解:小彤这学期的体育成绩为=(20×95+30×90+50×94)=93(分).
故选D.
【点评】本题考查了折线统计图以及加权平均数,解题的关键是利用加权平均数的公式求出小彤这学期的体育成绩.本题属于基础题,难度不大,解决该题型题目时,熟记加权平均数的公式是解题的关键.
8.(2015?河南)小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分、80分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )
A.255分 B.84分 C.84.5分 D.86分
【分析】根据题意列出算式,计算即可得到结果.
【解答】解:根据题意得:85×+80×+90×=17+24+45=86(分),
故选D
【点评】此题考查了加权平均数,熟练掌握加权平均数的求法是解本题的关键.
9.(2015?玉林)学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )
A.2 B.2.8 C.3 D.3.3
【分析】平均数的计算方法是求出所有数据的和,然后除以数据的总个数.注意本题不是求3,5,11,11这四个数的平均数.
【解答】解:(3×1+5×2+11×3+11×4)÷30
=(3+10+33+44)÷30
=90÷30
=3.
故30名学生参加活动的平均次数是3.
故选:C.
【点评】本题考查加权平均数,条形统计图和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
10.(2015?河北区二模)某年级有四个班,人数分别为:一班25人,二班22人,三班27人,四班26人.在一次考试中,四个班的班级平均分依次为81分,75分,89分,78分,则这次考试的年级平均分为( )
A.79.25分 B.80.75分 C.81.06分 D.82.53分
【分析】平均数的计算方法是求出所有学生的总分之和,然后除以学生总数.
【解答】解:该组数据的平均数==81.06分;
故选C.
【点评】本题考查的是加权平均数的求法.本题易出现的错误是求81,89,78,75这四个数的平均数,对平均数的理解不正确.
二.填空题(共4小题)
11.(2016?黄冈校级自主招生)设有四个数,其中每三个数的和分别为24,36,28,32.则这四个数的平均数为 10 .
【分析】可以设这四个数分别是a,b,c,d,根据条件就可列方程组,从而根据平均数的计算公式求解.
【解答】解:设这四个数分别是a,b,c,d,
根据题意得:
四个式子相加得:a+b+c+d=40
则平均数是=10
故答案是:10.
【点评】本题主要考查了平均数的计算方法,正确解方程组是解题的关键.
12.(2015?玄武区一模)若李老师六个月的手机上网流量(单位:M)分别为526,600,874,480,620,500,则李老师这六个月平均每个月的手机上网流量为 600 M.
【分析】只要运用求平均数公式:即可求出答案.
【解答】解:根据题意得:
(526+600+874+480+620+500)÷6=600(M);
答:李老师这六个月平均每个月的手机上网流量为600M;
故答案为:600.
【点评】本题考查的是算术平均数的求法.熟记公式是解决本题的关键.
13.(2016春?睢宁县校级月考)如图显示是某班20人在“献爱心”活动中捐图书的情况,该班人均捐了 2.8 册.
【分析】根据条形统计图可算出捐2本书的人数,再利用加权平均数的公式即可算出该班人均捐书本书.
【解答】解:捐2本书的人数为:20﹣2﹣4﹣4﹣2=8(人),
该班人均捐书本数为:×(1×2+2×8+3×4+4×4+5×2)=2.8(本).
故答案为:2.8.
【点评】本题考查了加权平均数以及条形统计图,解题的关键是结合调休统计图求出捐2本书的人数.本题属于基础题,难度不大,解决该题型题目时,能够熟练运用加权平均数公式解决问题是关键.
14.(2015春?防城区期末)小王某学期的物理成绩分别为:平时平均成绩得84分,期中考试得90分,期末考试得85 分.若按如图所显示的权重,那么小王该学期的总评成绩应该为 86.4 分.
【分析】根据加权平均数的计算公式列出算式,再进行计算即可.
【解答】解:根据题意得:
84×10%+90×30%+85×60%=86.4(分),
答:小王该学期的总评成绩应该为86.4分.
故答案为:86.4.
【点评】此题考查了加权平均数,本题易出现的错误是求84,90,85的平均数,对加权平均数的理解不正确.
三.解答题(共6小题)
15.(2014春?萧山区校级月考)有一组数据:3,x2+1,5,2x﹣3,4,它们的平均数是4,求x的值.
【分析】由平均数的定义可得x的方程,解方程可得.
【解答】解:由题意可得3+x2+1+5+2x﹣3+4=4×5,
整理,得x2+2x﹣10=0,
解得x1=﹣1+,x2=﹣1﹣.
即所求x的值为﹣1+或﹣1﹣.
【点评】本题考查平均数的定义,平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.本题是基础题.
16.(2016春?洛江区期末)某学校设立学生奖学金时规定:综合成绩最高者得一等奖,综合成绩包括体育成绩、德育成绩、学习成绩三项,这三项成绩分别按1:3:6的比例计入综合成绩.小明、小亮两位同学入围测评,他们的体育成绩、德育成绩、学习成绩如下表.请你通过计算他们的综合成绩,判断谁能拿到一等奖?
体育成绩
德育成绩
学习成绩
小明
96
94
90
小亮
90
93
92
【分析】根据加权平均数的定义分别计算两人的加权平均数,然后比较大小即可.
【解答】解:小明的综合成绩=0.1×96+0.3×94+0.6×90=91.8,
小亮的综合成绩=0.1×90+0.3×93+0.6×92=92.1,
∵92.1>91.8,
∴小亮能拿到一等奖.
【点评】本题考查了加权平均数:若n个数x1,x2,x3,…,xn的权分别是w1,w2,w3,…,wn,则(x1w1+x2w2+…+xnwn)÷(w1+w2+…+wn)叫做这n个数的加权平均数.
17.将若干由1开始的连续自然数写在纸上,然后删去其中一个数,则余下的数的平均数为53,问删去的那个数是多少?
【分析】基于平均数的考虑:1,2,3,4,…,105的平均数是53,1,2,3,4,…,106的平均数是53.5,它应该有105个或106个连续数,由于减去一个数的平均为53,当n=105个,但104×53不是整数,故否定了有105个数.当106个数时,可以尝试错误法找出.
【解答】解:1,2,3,4,….,105的平均数是53,
1,2,3,4,….,106的平均数是53.5
它应该有105个或106个连续数.
(1)由于减去一个数的平均为53,当n=105个,但104×53不是整数,故否定了有105个数.
(2)当106个数时,很明显不会删去106,故应是1﹣105中其中一个数,考虑平均数的分数部,由于是105个数的平均,故将=,当中表示删去的数为106﹣45=61,或1+2+3+…+106=5671,
当减去一个数后,平均为53,n=105,
和=53×105=5610,
所以减去的一个数应是5671﹣5610=61.
答:删去的那个数是61.
【点评】本题考查的是样本平均数的求法及运用,解题的关键是先确定连续自然数介于105个或106个连续数,然后讨论即可.
18.一组数据a,1.8,2.2,1.8,b的平均数是1.96,求a,b两数的平均数.
【分析】由平均数的公式即可计算出a+b的值,进一步求得a,b两数的平均数即可.
【解答】解:由题意得:
×(1.8+2.2+1.8+a+b)=1.96,
解得a+b=4.
故a,b两数的平均数是4÷2=2.
【点评】本题考查了算术平均数的计算方法,解题的关键是正确的应用公式.
19.(2015春?惠安县期末)东升广告公司欲招聘广告策划人员一名,对甲、乙、丙三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
测试项目
测 试 成 绩
甲
乙
丙
创 新
72
85
67
综合知识
50
74
70
语 言
88
45
67
(1)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用?
(2)根据实际需要,公司将创新、综合知识、语言三项测试得分按扇形统计图所示比例确定甲、乙、丙三人的测试成绩,此时谁将被录用?
【分析】(1)先根据题意求出甲、乙、丙的平均成绩,再进行比较即可;
(2)按扇形统计图所示比例求出甲、乙、丙三人的测试成绩,再进行比较即可.
【解答】解:(1)∵甲三项测试的平均成绩为:(72+50+88)÷3=70,
乙三项测试的平均成绩为(85+74+45)÷3=68,
丙三项测试的平均成绩为(67+70+67)÷3=68;
∴甲将被录用.
(2)分别为:
甲:72×50%+50×30%+88×20%=68.6
乙:85×50%+74×30%+45×20%=73.7
丙:67×50%+70×30%+67×20%=67.9
∴乙将被录用.
【点评】此题考查了加权平均数,关键是根据题意列出算式,求出平均数,用到的知识点是加权平均数的计算公式.
20.(2015秋?滕州市校级期末)某班为了从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评,A、B、C、D、E五位老师作为评委,对“演讲答辩”情况进行了评价,全班50位同学参与了民主测评,结果如下表:
A
B
C
D
E
好
较好
一般
甲
90
92
94
95
88
甲
40
7
3
乙
89
86
87
94
91
乙
42
4
4
表一 演讲答辩得分 表二 民主测评得票
规则:①演讲答辩得分按“去掉一个最高分和一个最低分后,再算出平均分”的方法确定;②民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;③演讲答辩得分和民主测评得分按4:6确定权重,计算综合得分,请你计算一下甲、乙的综合得分,选出班长.
【分析】首先分别求出甲、乙两位选手各自演讲答辩的平均分,然后根据平均数的概念分别计算出甲、乙两位选手的民主测评分,最后根据不同权重计算加权成绩.
【解答】解:甲演讲答辩的平均分为:=92;
乙演讲答辩的平均分为:=89,
甲民主测评分为:40×2+7×1=87,
乙民主测评分为:42×2+4×1=88,
∴甲综合得分:=89,
∴乙综合得分:=88.4,
∵89>88.4,
∴应选择甲当班长.
【点评】本题考查了平均数和加权平均数的概念及应用,以及从表格中获取信息的能力.
