河北省平泉四海中学人教版八年级上册数学课件:12.3.2等边三角形
文档属性
| 名称 | 河北省平泉四海中学人教版八年级上册数学课件:12.3.2等边三角形 |

|
|
| 格式 | ppt | ||
| 文件大小 | 899.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-16 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
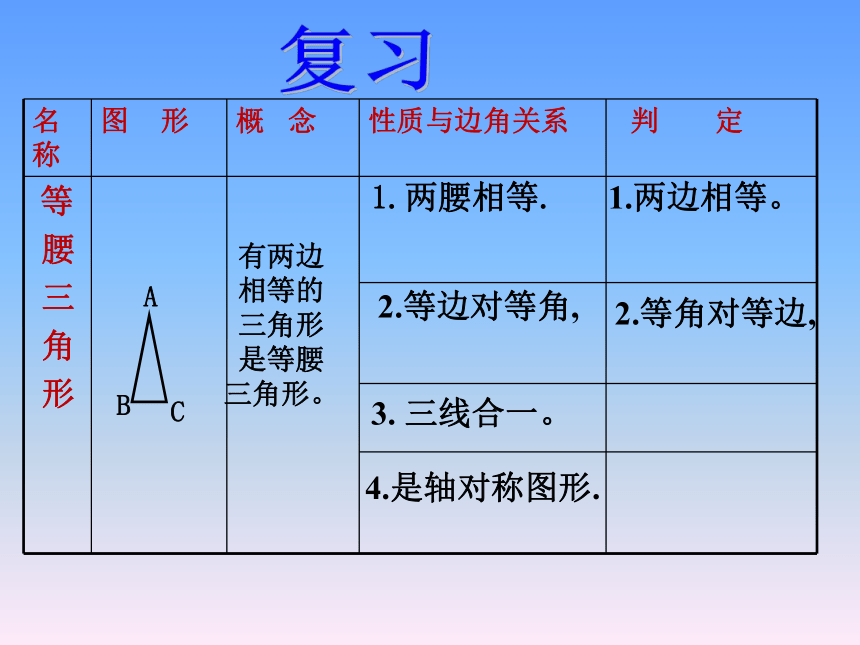
名称 图 形 概 念 性质与边角关系 判 定
等
腰
三
角
形
A
B
C
有两边相等的三角形是等腰三角形。
2.等边对等角,
3. 三线合一。
4.是轴对称图形.
2.等角对等边,
1.两边相等。
1.两腰相等.
等边三角形
在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边相等。
我们把三条边都相等的三角形
叫做等边三角形(正三角形)。
1.等边三角形的内角都相等吗 为什么
由已知:AB=AC=BC,
∵AB=AC
∴∠B=∠C (为什么 )
同理 ∠A=∠C
∴∠A=∠B=∠C
∵ ∠A+∠B+∠C=180°
∴ ∠A= ∠B= ∠C=60 °
结论:等边三角形的内角都相等,且等于60 °.
等边三角形性质探索:
A
B
C
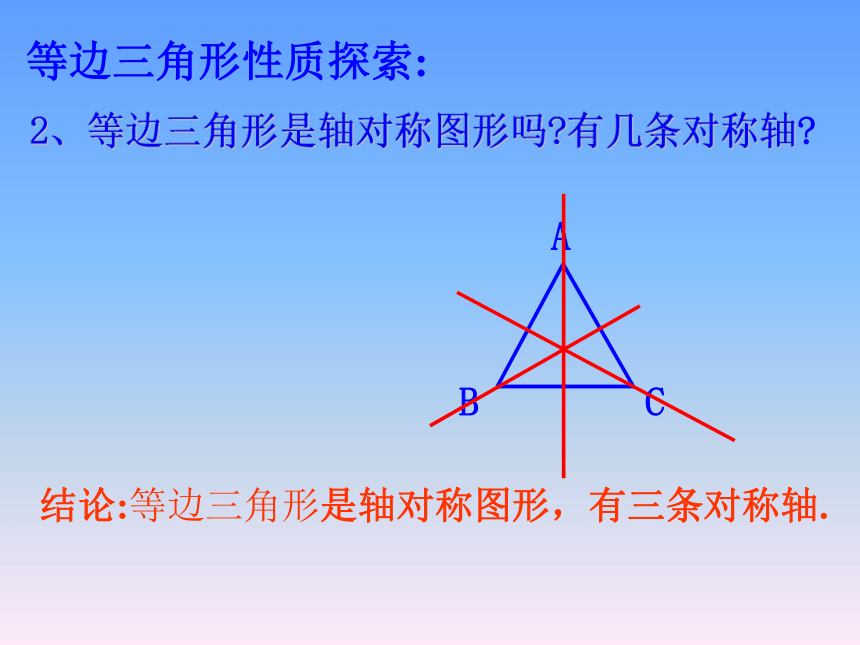
2、等边三角形是轴对称图形吗 有几条对称轴
结论:等边三角形是轴对称图形,有三条对称轴.
等边三角形性质探索:
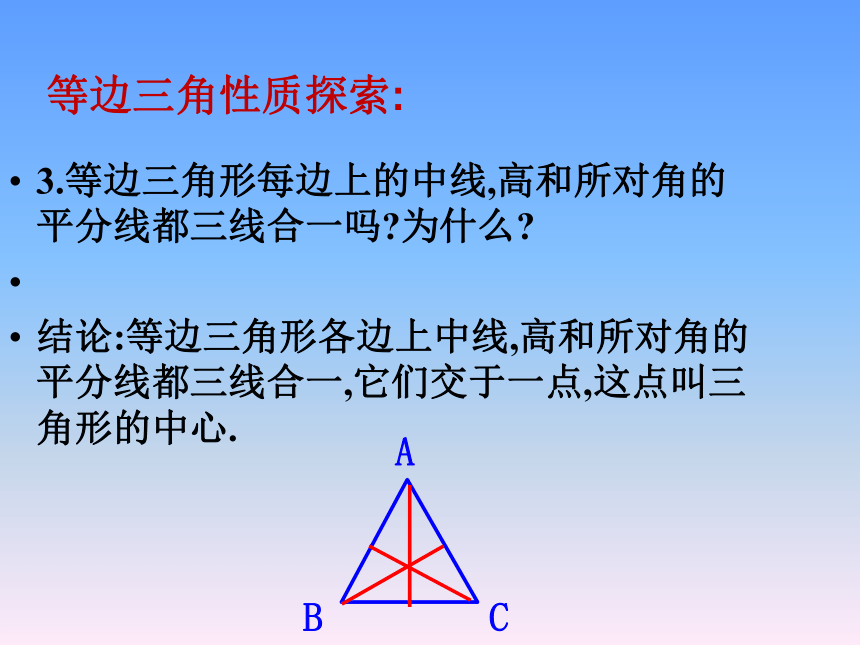
3.等边三角形每边上的中线,高和所对角的平分线都三线合一吗 为什么
结论:等边三角形各边上中线,高和所对角的平分线都三线合一,它们交于一点,这点叫三角形的中心.
等边三角性质探索:
等边三角形的性质
2.等边三角形的内角都相等,且等于60 °
3.等边三角形各边上中线,高和所对角的平分线都三线合一.
4.等边三角形是轴对称图形,有三条对称轴.
1 .三条边相等
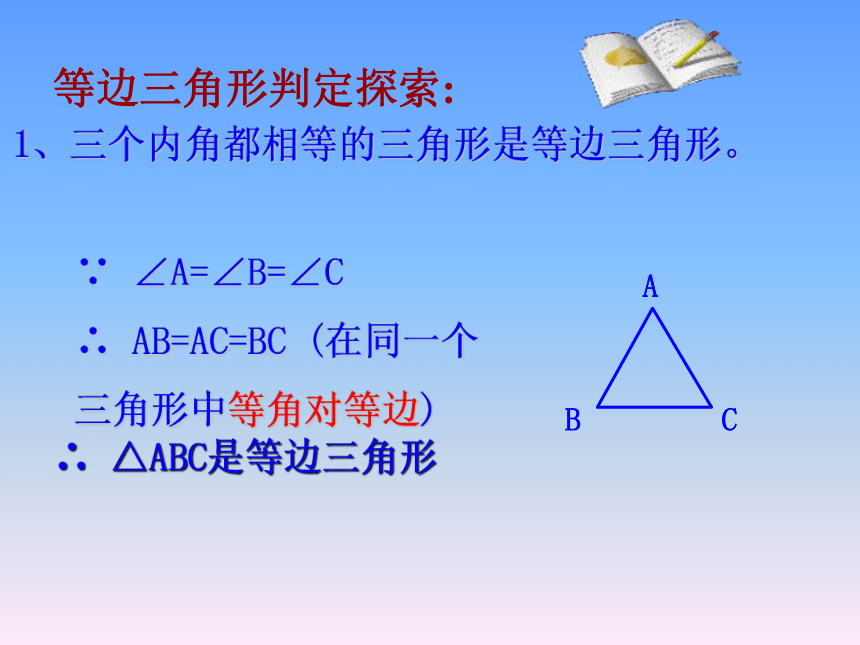
∵ ∠A=∠B=∠C
∴ AB=AC=BC (在同一个三角形中等角对等边)
1、三个内角都相等的三角形是等边三角形。
∴ △ABC是等边三角形
等边三角形判定探索:
2.有一个内角等于60 °的等腰三角形是等边三角形.
假若AB=AC.则∠ B= ∠ C
当顶角∠A=60 °时,
∠ B= ∠ C= 60 °
∴ ∠A= ∠ B= ∠ C=60 ° ∴ △ABC是等边三角形.
当底角∠ B= 60时,
∠ C=60 °, ∠A=180 —(60° +60 °)=60. °
∴ ∠A= ∠ B= ∠ C=60 ° ∴ △ABC是等边三角形.
A
B
C
1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
一般三角形
等边三角形
⒈ 三个角都相等的三角形是等边三角形.
⒉ 有一个角是60°的等腰三角形是等边
三角形.
等边三角形
等腰三角形
等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗
讨论
定义 性质 判定
等 腰
三 角 形
等 边
三 角 形
有二条边相等
1、两个底角相等
2、三线合一
3、对称轴一条
1、三个角都相等
2、三线合一
3、对称轴三条
有三条边相等
1、定义
2、等角对等边
1、定义
2、三个角都相等
3、等腰三角形有
一个角是600
1.已知:等边△ABC中,DB是AC边上的高,E是BC延长线上一点,且DB=DE,求∠ E的度数.
B
C
D
A
E
例题
2.如图, △ABC为等边三角形, ∠1=∠ 2=∠ 3
(1)求∠BEC的度数.
(2) △DEF为等边三角形吗 为什么
A
B
C
E
D
F
1
3
2
练 习
1、如图,在等边三角形ABC中AD⊥BC于D。以AD为一边,作等边三角形ADE,则DE与AC垂直吗?请说明理由。
2.如图,已知△ABC是等边三角形,D是AC的中点,EC⊥BC,且EC=BD。求证:△ADE是等边三角形
3.已知△ABC是等边三角形,D,E,F分别是各边上的一点,且AD=BE=CF.试说明△ DEF是等边三角形.
4.D,E是△ABC中BC上的两点,且BD=DE=EC=AD=AE.求∠ B与∠ BAC的度数.
A
D
C
F
B
E
A
B
D
E
C
5.如图,△ABC是等边三角形,P、Q分别是AC、BC上的 点,且AP=CQ,AQ与BP交于点M。求∠BMQ的度数。
(1).等边三角形的性质.
1.等边三角形的内角都相等,且等于60 °
2.等边三角形是轴对称图形,有三条对称.
3.等边三角形各边上中线,高和所对角的平 分线都三线合一.
(2) 等边三角形的判定:
1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
小结
名称 图 形 概 念 性质与边角关系 判 定
等
腰
三
角
形
A
B
C
有两边相等的三角形是等腰三角形。
2.等边对等角,
3. 三线合一。
4.是轴对称图形.
2.等角对等边,
1.两边相等。
1.两腰相等.
等边三角形
在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边相等。
我们把三条边都相等的三角形
叫做等边三角形(正三角形)。
1.等边三角形的内角都相等吗 为什么
由已知:AB=AC=BC,
∵AB=AC
∴∠B=∠C (为什么 )
同理 ∠A=∠C
∴∠A=∠B=∠C
∵ ∠A+∠B+∠C=180°
∴ ∠A= ∠B= ∠C=60 °
结论:等边三角形的内角都相等,且等于60 °.
等边三角形性质探索:
A
B
C
2、等边三角形是轴对称图形吗 有几条对称轴
结论:等边三角形是轴对称图形,有三条对称轴.
等边三角形性质探索:
3.等边三角形每边上的中线,高和所对角的平分线都三线合一吗 为什么
结论:等边三角形各边上中线,高和所对角的平分线都三线合一,它们交于一点,这点叫三角形的中心.
等边三角性质探索:
等边三角形的性质
2.等边三角形的内角都相等,且等于60 °
3.等边三角形各边上中线,高和所对角的平分线都三线合一.
4.等边三角形是轴对称图形,有三条对称轴.
1 .三条边相等
∵ ∠A=∠B=∠C
∴ AB=AC=BC (在同一个三角形中等角对等边)
1、三个内角都相等的三角形是等边三角形。
∴ △ABC是等边三角形
等边三角形判定探索:
2.有一个内角等于60 °的等腰三角形是等边三角形.
假若AB=AC.则∠ B= ∠ C
当顶角∠A=60 °时,
∠ B= ∠ C= 60 °
∴ ∠A= ∠ B= ∠ C=60 ° ∴ △ABC是等边三角形.
当底角∠ B= 60时,
∠ C=60 °, ∠A=180 —(60° +60 °)=60. °
∴ ∠A= ∠ B= ∠ C=60 ° ∴ △ABC是等边三角形.
A
B
C
1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
一般三角形
等边三角形
⒈ 三个角都相等的三角形是等边三角形.
⒉ 有一个角是60°的等腰三角形是等边
三角形.
等边三角形
等腰三角形
等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗
讨论
定义 性质 判定
等 腰
三 角 形
等 边
三 角 形
有二条边相等
1、两个底角相等
2、三线合一
3、对称轴一条
1、三个角都相等
2、三线合一
3、对称轴三条
有三条边相等
1、定义
2、等角对等边
1、定义
2、三个角都相等
3、等腰三角形有
一个角是600
1.已知:等边△ABC中,DB是AC边上的高,E是BC延长线上一点,且DB=DE,求∠ E的度数.
B
C
D
A
E
例题
2.如图, △ABC为等边三角形, ∠1=∠ 2=∠ 3
(1)求∠BEC的度数.
(2) △DEF为等边三角形吗 为什么
A
B
C
E
D
F
1
3
2
练 习
1、如图,在等边三角形ABC中AD⊥BC于D。以AD为一边,作等边三角形ADE,则DE与AC垂直吗?请说明理由。
2.如图,已知△ABC是等边三角形,D是AC的中点,EC⊥BC,且EC=BD。求证:△ADE是等边三角形
3.已知△ABC是等边三角形,D,E,F分别是各边上的一点,且AD=BE=CF.试说明△ DEF是等边三角形.
4.D,E是△ABC中BC上的两点,且BD=DE=EC=AD=AE.求∠ B与∠ BAC的度数.
A
D
C
F
B
E
A
B
D
E
C
5.如图,△ABC是等边三角形,P、Q分别是AC、BC上的 点,且AP=CQ,AQ与BP交于点M。求∠BMQ的度数。
(1).等边三角形的性质.
1.等边三角形的内角都相等,且等于60 °
2.等边三角形是轴对称图形,有三条对称.
3.等边三角形各边上中线,高和所对角的平 分线都三线合一.
(2) 等边三角形的判定:
1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
小结
