河北省平泉四海中学人教版八年级上册数学课件:13.1.1轴对称
文档属性
| 名称 | 河北省平泉四海中学人教版八年级上册数学课件:13.1.1轴对称 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-16 00:00:00 | ||
图片预览










文档简介
(共35张PPT)
引言 对称现象无处不在,从自然景观到艺术作
品,从建筑物到交通标志,甚至日常生活用品,都可
以找到对称的例子,对称给我们带来美的感受!
引出新知
探索新知
问题1 如图,把一张纸对折,剪出一个图案(折
痕处不要完全剪断),再打开这张对折的纸,就得到了
美丽的窗花.观察得到的窗花,你能发现它们有什么共
同的特点吗?
追问 你能举出一些轴对称图形的例子吗?
探索新知
如果一个平面图形沿一条直线折叠,直线两旁的部
分能够互相重合,这个图形就叫做轴对称图形,这条直
线就是它的对称轴.这时,我们也说这个图形关于这条
直线(成轴)对称.
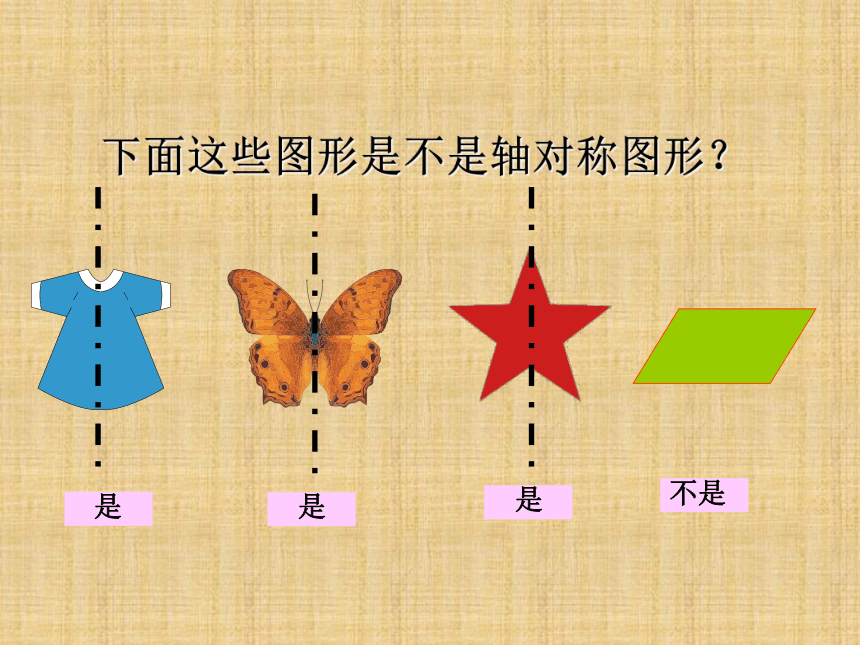
下面这些图形是不是轴对称图形?
是
是
是
不是
下面四幅图中是轴对称的有几个?
√
√
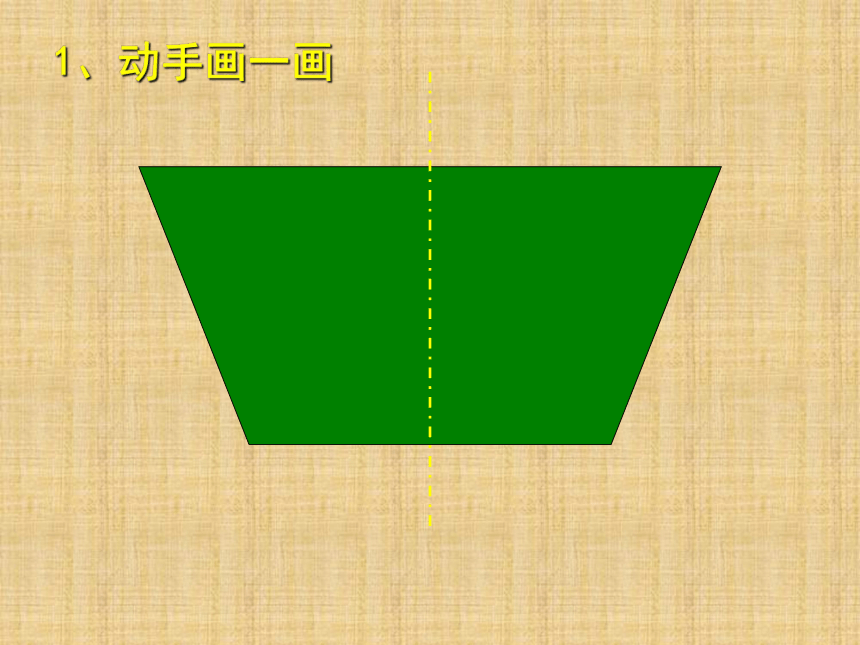
1、动手画一画
图形 形状 是否轴对称图形 对称轴的数量(条)
长方形
正方形
平行四边形
等腰三角形
圆形
是
是
是
是
不是
2
4
1
无数
-------
小结
(1)有些轴对称图形的对称轴只有一条,但有的轴对称图形的对称轴却不止一条,有的轴对称图形的对称轴甚至有无数条。
(2)对称轴通常画成虚线,是直线,不能画成线段。
画出下面每个轴对称图形的对称轴
共同特征:
每一对图形沿着虚线折叠,左边的图形都能与右边的图形重合.
探索新知
问题2 观察下面每对图形(如图),你能类比前
面的内容概括出它们的共同特征吗?
追问1 你能再举出一些两个图形成轴对称的例子吗?
探索新知
把一个图形沿着某一条直线折叠,如果它能够与另
一个图形重合,那么就说这两个图形关于这条直线(成
轴)对称,这条直线叫做对称轴,折叠后重合的点是对
应点,叫做对称点.
两者的联系:
把成轴对称的两个图形看成一个整体,它就是一个
轴对称图形.把一个轴对称图形沿对称轴分成两个图
形,这两个图形关于这条轴对称.
探索新知
追问2 你能结合具体的图形说明轴对称图形和两个
图形成轴对称有什么区别与联系吗?
两者的区别:
轴对称图形指的是一个图形沿对称轴折叠后这个图
形的两部分能完全重合,而两个图形成轴对称指的是两
个图形之间的位置关系,这两个图形沿对称轴折叠后能
够重合.
探索新知
追问2 你能结合具体的图形说明轴对称图形和两个
图形成轴对称有什么区别与联系吗?
追问1 你能说明其中
的道理吗?
探索新知
问题3 如图,△ABC 和△A′B′C′关于直线MN
对称,点A′,B′,C′分别是点A,B,C 的对称点,线
段AA′,BB′,CC′与直线MN 有什么关系?
A
B
C
M
N
P
A′
B′
C′
探索新知
追问2 上面的问题说明“如果△ABC 和
△A′B′C′关于直线MN 对称,那么,直线MN 垂直
线段AA′,BB′和CC′,并且直线MN 还平分线段
AA′,BB′和CC′”.如
果将其中的“三角形”改为
“四边形”“五边形”…其
他条件不变,上述结论还成
立吗?
A
B
C
M
N
P
A′
B′
C′
经过线段中点并且垂直
于这条线段的直线,叫做这
条线段的垂直平分线.
探索新知
问题3 如图,△ABC 和△A′B′C′关于直线MN
对称,点A′,B′,C′分别是点A,B,C 的对称点,线
段AA′,BB′,CC′与直线MN 有什么关系?
A
B
C
M
N
P
A′
B′
C′
探索新知
追问3 你能用数学语言概括前面的结论吗?
成轴对称的两个图形的性质:
如果两个图形关于某条
直线对称,那么对称轴是任
何一对对应点所连线段的垂
直平分线.即对称点所连线
段被对称轴垂直平分;对称
轴垂直平分对称点所连线段.
A
B
C
M
N
P
A′
B′
C′
结论:
直线l 垂直线段AA′,BB′,
直线l平分线段AA′,BB′(或直
线l 是线段AA′,BB′的垂直平分
线).
探索新知
问题4 下图是一个轴对称图形,你能发现什么结
论?能说明理由吗?
A
B
l
A′
B′
追问 你能用数学语言概括前面
的结论吗?
探索新知
问题4 下图是一个轴对称图形,你能发现什么结
论?能说明理由吗?
A
B
l
A′
B′
轴对称图形的性质:
轴对称图形的对称轴,是任何
一对对应点所连线段的垂直平分线.
探索新知
问题4 下图是一个轴对称图形,你能发现什么结
论?能说明理由吗?
A
B
l
A′
B′
课堂练习
练习1 如图所示的每个图形是轴对称图形吗?如
果是,指出它的对称轴.
课堂练习
练习2 如图所示的每幅图形中的两个图案是轴对称
的吗?如果是,试着找出它们的对称轴,并找出一对对称点.
八年级 数学
第十二章 轴对称
a
3.如图,△ABC与△DEF关于直线a对称,若AB=2cm,∠BCA=55°,则DE= ___ ,∠DFE= 。
a
A
B
C
F
E
D
2cm
55°
a
A
B
C
F
E
D
4.如图,长方形ABCD沿着AE折叠,使点D落在BC边上的F点处,如果∠BAF=60°求∠DAE,∠AEF的度数。
图1
图2
5.把一圆形纸片两次对折后,得到右图,然后沿虚线剪开,得到两部分,其中一部分展开后的平面图形是( )
A
B
C
D
B
比较归纳:
轴对称图形 两个图形成轴对称
区别 _个图形 _个图形
联
系 1.沿一条直线折叠,直线两旁的部分能够____.
2.都有____.
3.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条直线___;如果把两个成轴对称的图形看成一个图形,那么这个图形就是____.
一
两
互相重合
对称轴
对称
轴对称图形
引言 对称现象无处不在,从自然景观到艺术作
品,从建筑物到交通标志,甚至日常生活用品,都可
以找到对称的例子,对称给我们带来美的感受!
引出新知
探索新知
问题1 如图,把一张纸对折,剪出一个图案(折
痕处不要完全剪断),再打开这张对折的纸,就得到了
美丽的窗花.观察得到的窗花,你能发现它们有什么共
同的特点吗?
追问 你能举出一些轴对称图形的例子吗?
探索新知
如果一个平面图形沿一条直线折叠,直线两旁的部
分能够互相重合,这个图形就叫做轴对称图形,这条直
线就是它的对称轴.这时,我们也说这个图形关于这条
直线(成轴)对称.
下面这些图形是不是轴对称图形?
是
是
是
不是
下面四幅图中是轴对称的有几个?
√
√
1、动手画一画
图形 形状 是否轴对称图形 对称轴的数量(条)
长方形
正方形
平行四边形
等腰三角形
圆形
是
是
是
是
不是
2
4
1
无数
-------
小结
(1)有些轴对称图形的对称轴只有一条,但有的轴对称图形的对称轴却不止一条,有的轴对称图形的对称轴甚至有无数条。
(2)对称轴通常画成虚线,是直线,不能画成线段。
画出下面每个轴对称图形的对称轴
共同特征:
每一对图形沿着虚线折叠,左边的图形都能与右边的图形重合.
探索新知
问题2 观察下面每对图形(如图),你能类比前
面的内容概括出它们的共同特征吗?
追问1 你能再举出一些两个图形成轴对称的例子吗?
探索新知
把一个图形沿着某一条直线折叠,如果它能够与另
一个图形重合,那么就说这两个图形关于这条直线(成
轴)对称,这条直线叫做对称轴,折叠后重合的点是对
应点,叫做对称点.
两者的联系:
把成轴对称的两个图形看成一个整体,它就是一个
轴对称图形.把一个轴对称图形沿对称轴分成两个图
形,这两个图形关于这条轴对称.
探索新知
追问2 你能结合具体的图形说明轴对称图形和两个
图形成轴对称有什么区别与联系吗?
两者的区别:
轴对称图形指的是一个图形沿对称轴折叠后这个图
形的两部分能完全重合,而两个图形成轴对称指的是两
个图形之间的位置关系,这两个图形沿对称轴折叠后能
够重合.
探索新知
追问2 你能结合具体的图形说明轴对称图形和两个
图形成轴对称有什么区别与联系吗?
追问1 你能说明其中
的道理吗?
探索新知
问题3 如图,△ABC 和△A′B′C′关于直线MN
对称,点A′,B′,C′分别是点A,B,C 的对称点,线
段AA′,BB′,CC′与直线MN 有什么关系?
A
B
C
M
N
P
A′
B′
C′
探索新知
追问2 上面的问题说明“如果△ABC 和
△A′B′C′关于直线MN 对称,那么,直线MN 垂直
线段AA′,BB′和CC′,并且直线MN 还平分线段
AA′,BB′和CC′”.如
果将其中的“三角形”改为
“四边形”“五边形”…其
他条件不变,上述结论还成
立吗?
A
B
C
M
N
P
A′
B′
C′
经过线段中点并且垂直
于这条线段的直线,叫做这
条线段的垂直平分线.
探索新知
问题3 如图,△ABC 和△A′B′C′关于直线MN
对称,点A′,B′,C′分别是点A,B,C 的对称点,线
段AA′,BB′,CC′与直线MN 有什么关系?
A
B
C
M
N
P
A′
B′
C′
探索新知
追问3 你能用数学语言概括前面的结论吗?
成轴对称的两个图形的性质:
如果两个图形关于某条
直线对称,那么对称轴是任
何一对对应点所连线段的垂
直平分线.即对称点所连线
段被对称轴垂直平分;对称
轴垂直平分对称点所连线段.
A
B
C
M
N
P
A′
B′
C′
结论:
直线l 垂直线段AA′,BB′,
直线l平分线段AA′,BB′(或直
线l 是线段AA′,BB′的垂直平分
线).
探索新知
问题4 下图是一个轴对称图形,你能发现什么结
论?能说明理由吗?
A
B
l
A′
B′
追问 你能用数学语言概括前面
的结论吗?
探索新知
问题4 下图是一个轴对称图形,你能发现什么结
论?能说明理由吗?
A
B
l
A′
B′
轴对称图形的性质:
轴对称图形的对称轴,是任何
一对对应点所连线段的垂直平分线.
探索新知
问题4 下图是一个轴对称图形,你能发现什么结
论?能说明理由吗?
A
B
l
A′
B′
课堂练习
练习1 如图所示的每个图形是轴对称图形吗?如
果是,指出它的对称轴.
课堂练习
练习2 如图所示的每幅图形中的两个图案是轴对称
的吗?如果是,试着找出它们的对称轴,并找出一对对称点.
八年级 数学
第十二章 轴对称
a
3.如图,△ABC与△DEF关于直线a对称,若AB=2cm,∠BCA=55°,则DE= ___ ,∠DFE= 。
a
A
B
C
F
E
D
2cm
55°
a
A
B
C
F
E
D
4.如图,长方形ABCD沿着AE折叠,使点D落在BC边上的F点处,如果∠BAF=60°求∠DAE,∠AEF的度数。
图1
图2
5.把一圆形纸片两次对折后,得到右图,然后沿虚线剪开,得到两部分,其中一部分展开后的平面图形是( )
A
B
C
D
B
比较归纳:
轴对称图形 两个图形成轴对称
区别 _个图形 _个图形
联
系 1.沿一条直线折叠,直线两旁的部分能够____.
2.都有____.
3.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条直线___;如果把两个成轴对称的图形看成一个图形,那么这个图形就是____.
一
两
互相重合
对称轴
对称
轴对称图形
