人教版九年级上册22.1二次函数的图象和性质课件
文档属性
| 名称 | 人教版九年级上册22.1二次函数的图象和性质课件 |  | |
| 格式 | zip | ||
| 文件大小 | 95.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-17 09:25:38 | ||
图片预览


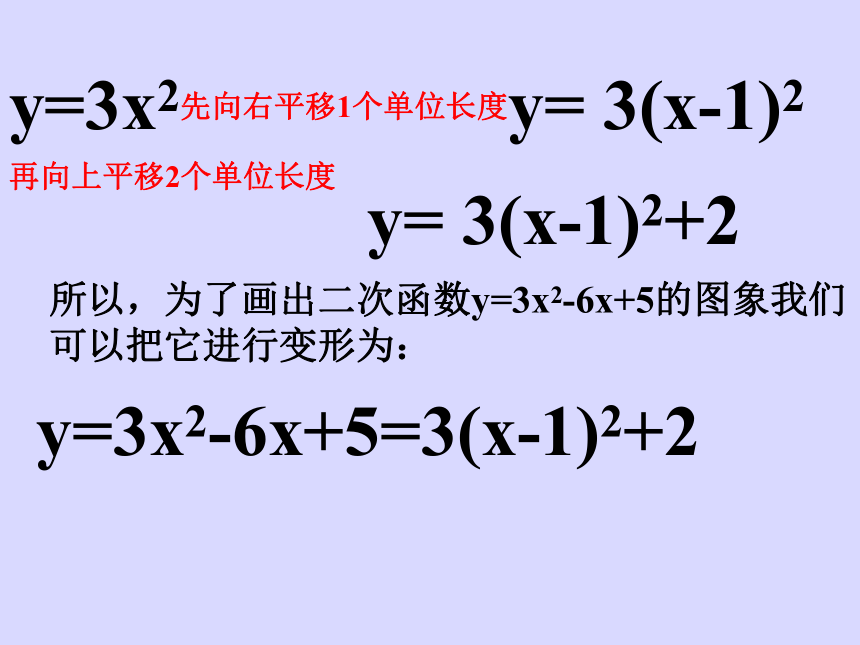

文档简介
课件14张PPT。二次函数
二次函数y=ax2+bx+c 的图象我们已经学习了解了一些简单的二次函数的
图象及其特点,比如,y=3x2,
y=3x2+2的图象特点。那么,二次函数y=3x2-6x+5 的图象
又是什么形状呢?与我们以前作过的二次函数
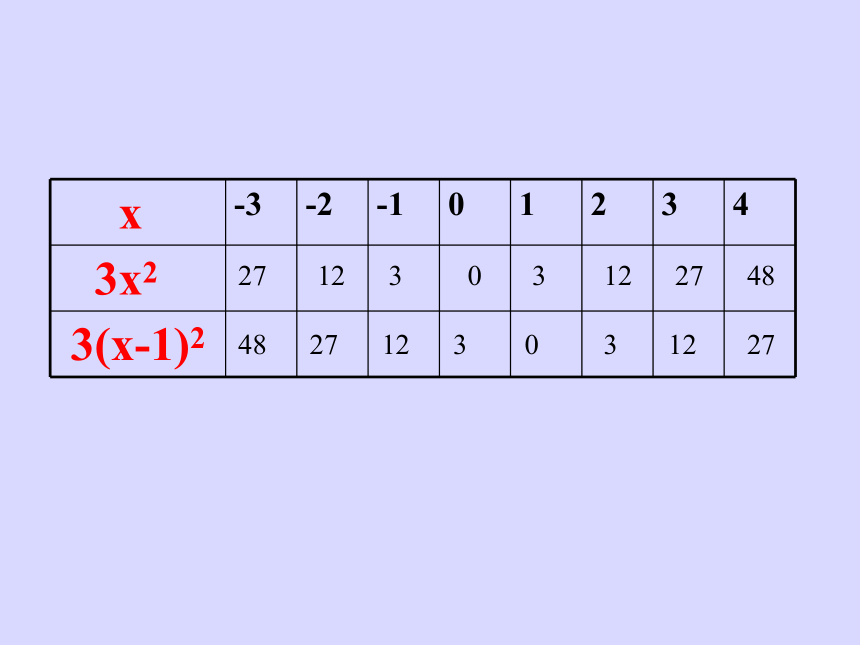
的图象有什么关系?y= 3x2
y= 3(x-1)2
12 3 0 3 12 27 48
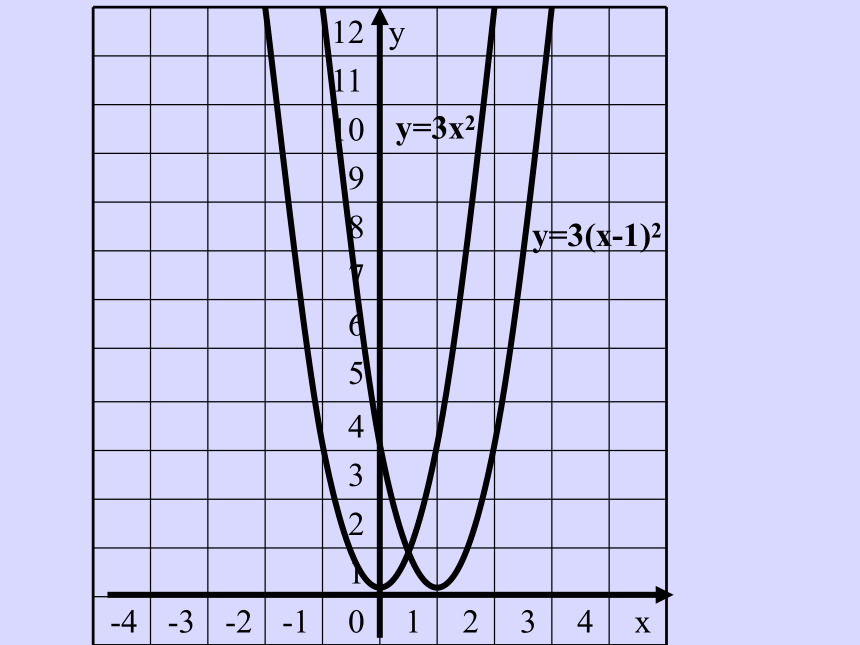
48 27 12 3 0 3 12 27y=3x2y=3(x-1)2y=3x2先向右平移1个单位长度y= 3(x-1)2
再向上平移2个单位长度y= 3(x-1)2+2
所以,为了画出二次函数y=3x2-6x+5的图象我们
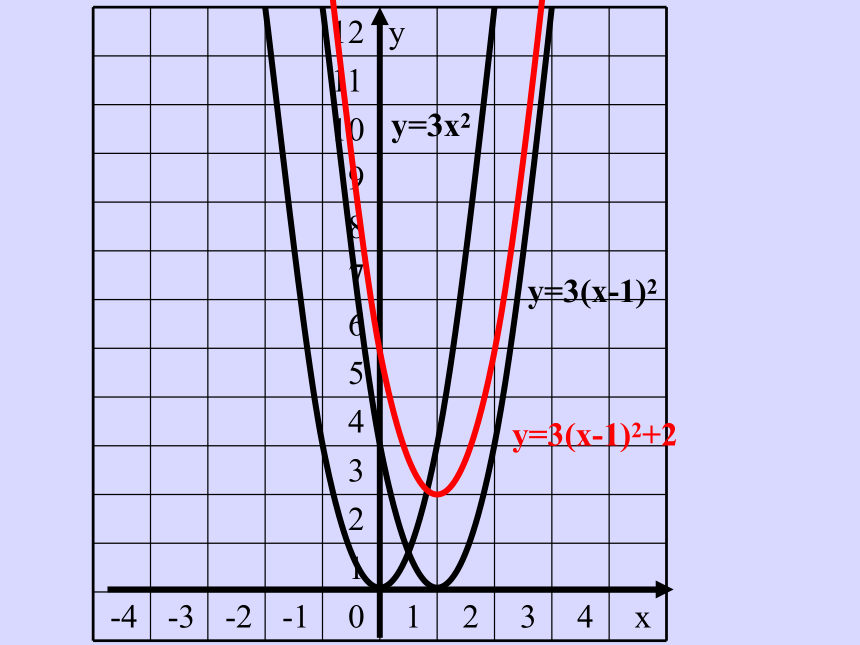
可以把它进行变形为:y=3x2-6x+5=3(x-1)2+2
y=3x2y=3(x-1)2+2y=3(x-1)2我们发现:二次函数y=3x2-6x+5的图象的对称轴
为 顶点坐标为
直线x=1(1, 2) 现在你知道怎样确定二次函数y=3x2-6x+5
=3(x-1)2+2的基本图象了吗?
那么二次函数y= 3(x+1)2与y= 3x2的
图象又有怎样的联系呢?可以通过
平移而得到吗? 想一想:y=3x2y=3(x+1)2议一议(1)二次函数y= -3(x-2)2+4的图象与二次函数y= -3x2
的图象有什么关系?它是轴对称图形吗?它的对称
轴和顶点坐标分别是什么? (2)对于二次函数y= 3(x+1)2,当x取哪些值时,
y的值随x值的增大而增大?当x取哪些值时,y的值
随x值的增大而减小? y= 3(x+1)2+4呢?
一般地,平移二次函数y= ax2的图象便可以得到
二次函数y= a(x-h)2+k的图象.因此,二次函数
y= a(x-h)2+k的图象是一条抛物线,它的开口方向、
对称轴和顶点坐标与a,h,k的值有关。填写下表: 向上 直线x=h (h,k)
向下 直线x=h (h,k)练一练
指出下列二次函数图象的开口方向、对称轴
和顶点坐标 。 (1) y=2(x-3)2- 0.5(2) y=-0.2(x+1)2- 5你从今天的学习中收获了什么?
你会作二次函数的图象吗?
二次函数y=ax2+bx+c 的图象我们已经学习了解了一些简单的二次函数的
图象及其特点,比如,y=3x2,
y=3x2+2的图象特点。那么,二次函数y=3x2-6x+5 的图象
又是什么形状呢?与我们以前作过的二次函数
的图象有什么关系?y= 3x2
y= 3(x-1)2
12 3 0 3 12 27 48
48 27 12 3 0 3 12 27y=3x2y=3(x-1)2y=3x2先向右平移1个单位长度y= 3(x-1)2
再向上平移2个单位长度y= 3(x-1)2+2
所以,为了画出二次函数y=3x2-6x+5的图象我们
可以把它进行变形为:y=3x2-6x+5=3(x-1)2+2
y=3x2y=3(x-1)2+2y=3(x-1)2我们发现:二次函数y=3x2-6x+5的图象的对称轴
为 顶点坐标为
直线x=1(1, 2) 现在你知道怎样确定二次函数y=3x2-6x+5
=3(x-1)2+2的基本图象了吗?
那么二次函数y= 3(x+1)2与y= 3x2的
图象又有怎样的联系呢?可以通过
平移而得到吗? 想一想:y=3x2y=3(x+1)2议一议(1)二次函数y= -3(x-2)2+4的图象与二次函数y= -3x2
的图象有什么关系?它是轴对称图形吗?它的对称
轴和顶点坐标分别是什么? (2)对于二次函数y= 3(x+1)2,当x取哪些值时,
y的值随x值的增大而增大?当x取哪些值时,y的值
随x值的增大而减小? y= 3(x+1)2+4呢?
一般地,平移二次函数y= ax2的图象便可以得到
二次函数y= a(x-h)2+k的图象.因此,二次函数
y= a(x-h)2+k的图象是一条抛物线,它的开口方向、
对称轴和顶点坐标与a,h,k的值有关。填写下表: 向上 直线x=h (h,k)
向下 直线x=h (h,k)练一练
指出下列二次函数图象的开口方向、对称轴
和顶点坐标 。 (1) y=2(x-3)2- 0.5(2) y=-0.2(x+1)2- 5你从今天的学习中收获了什么?
你会作二次函数的图象吗?
同课章节目录
