人教版初中数学八年级下册 第十七章 勾股定理 17.1 勾股定理 勾股定理证明 课件
文档属性
| 名称 | 人教版初中数学八年级下册 第十七章 勾股定理 17.1 勾股定理 勾股定理证明 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-16 21:37:16 | ||
图片预览





文档简介
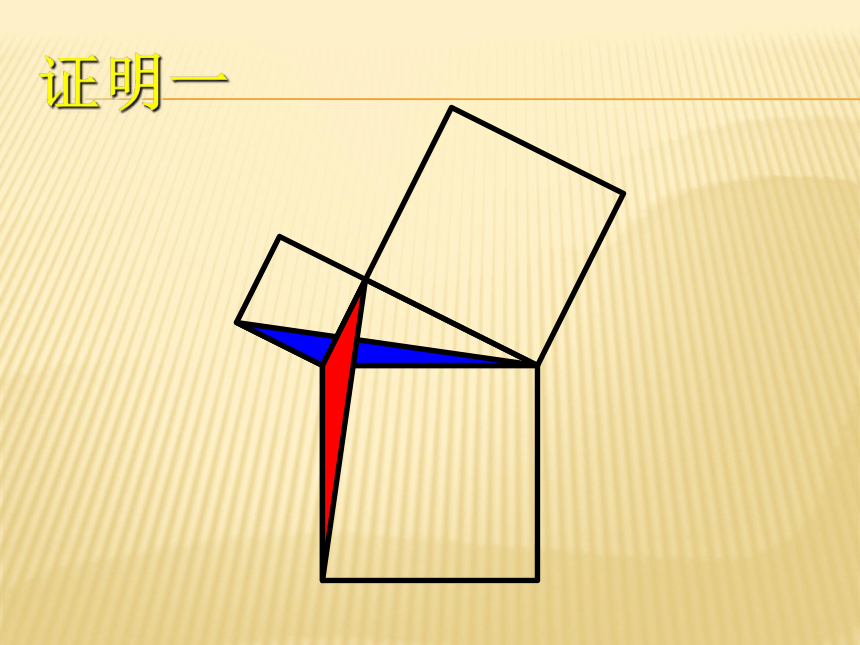
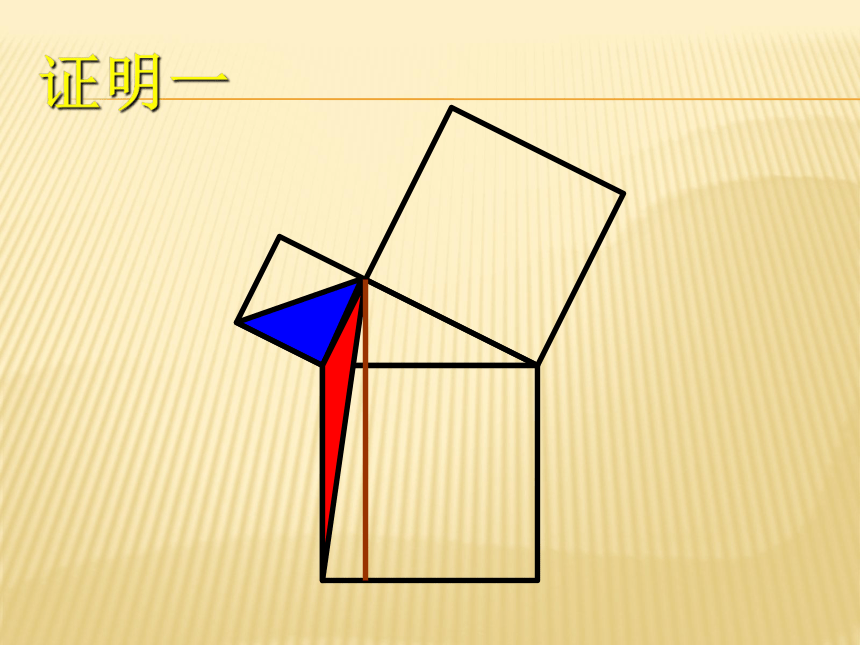
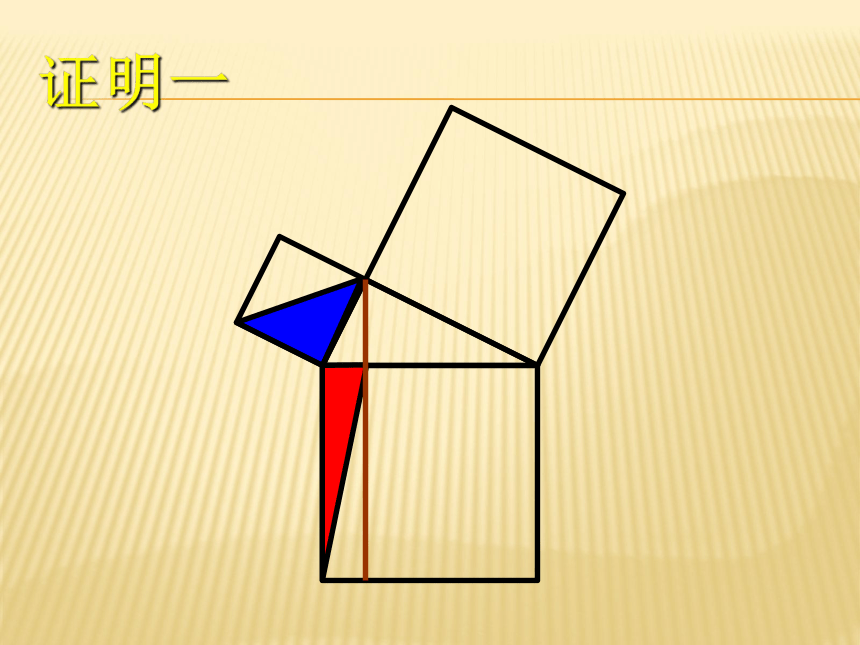
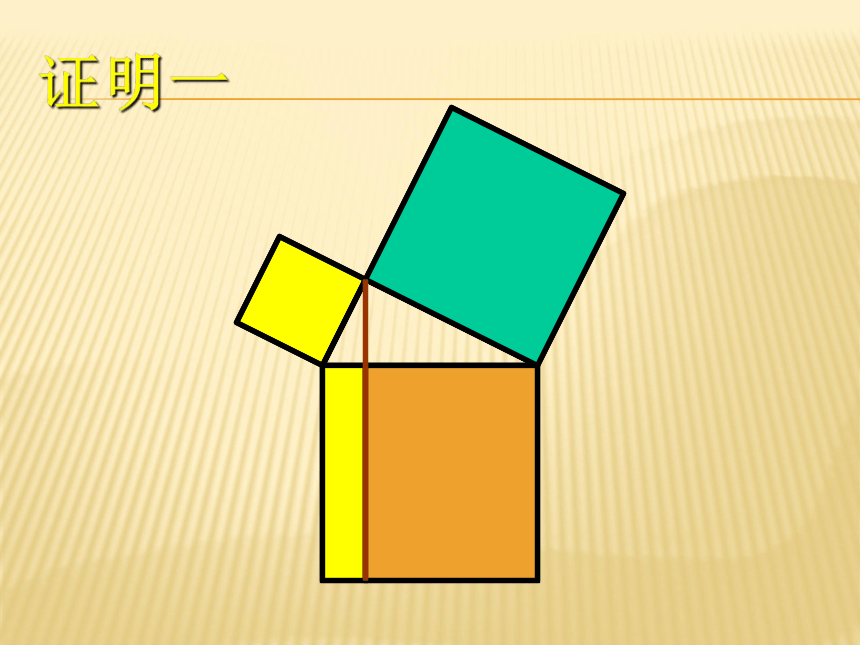
课件37张PPT。勾股定理证明 证明一证明一证明一证明一证明一几何原本欧几里得(Euclid of Alexandria; 约 325 B.C. ? 约 265 B.C.)
? 欧几里得的《几何原本》是用公理方法建立演绎数学体系的最早典范。
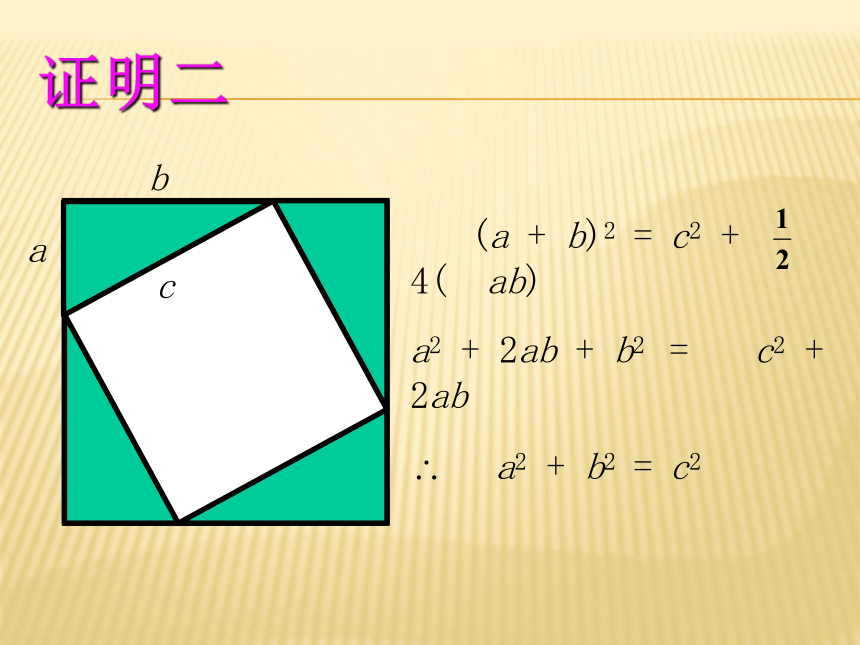
“证明一”就是取材自《几何原本》第一卷的第 47 命题。证明二ba (a + b)2 = c2 + 4( ab)
a2 + 2ab + b2 = c2 + 2ab
? a2 + b2 = c2c证明二cb ? a c2 = (a ? b)2 + 4( ab)
= a2 ? 2ab + b2 + 2ab
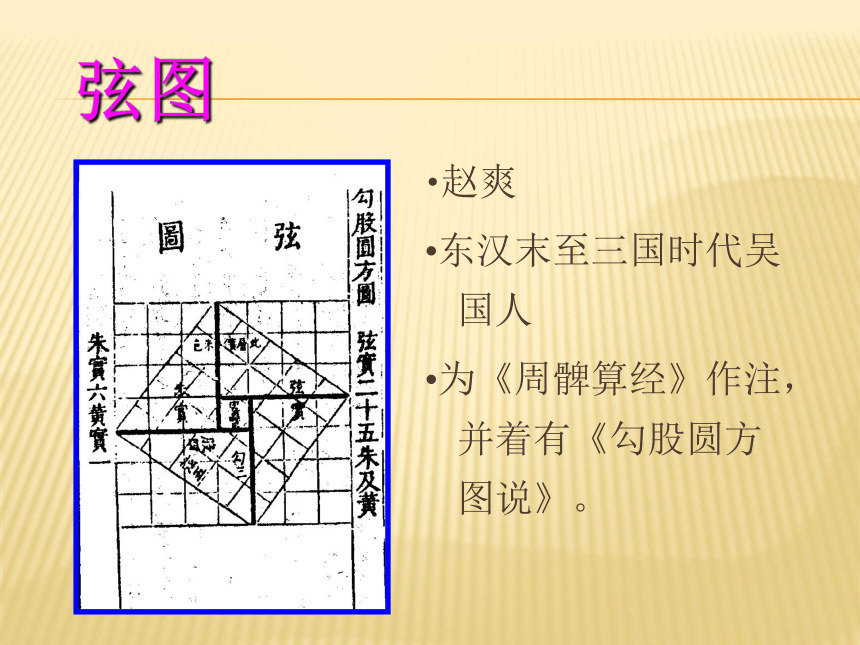
? c2 = a2 + b2弦图 ?赵爽
?东汉末至三国时代吴国人
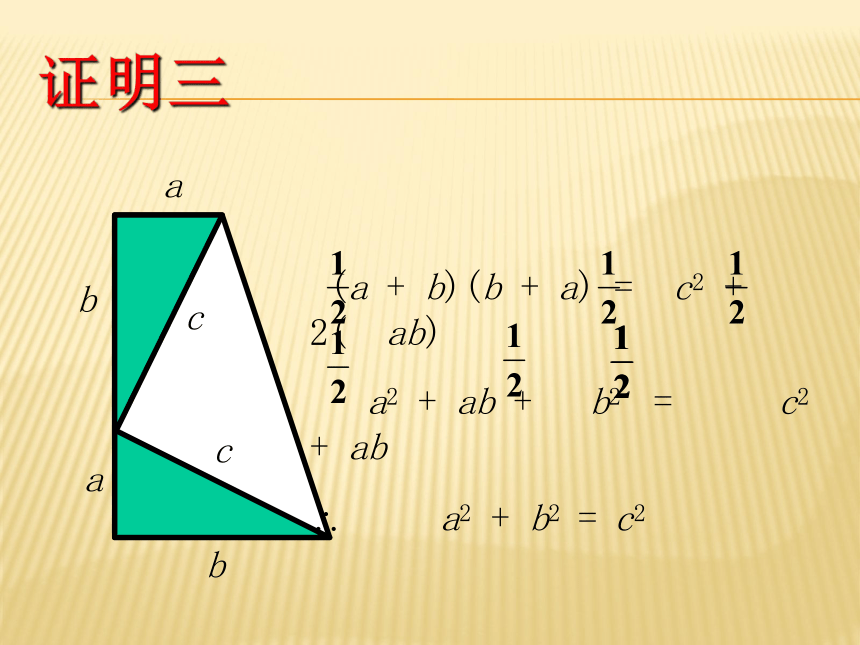
?为《周髀算经》作注,并着有《勾股圆方图说》。 证明三 (a + b)(b + a) = c2 + 2( ab)
a2 + ab + b2 = c2 + ab
? a2 + b2 = c2aabbcc美国总统的证明加菲尔德(James A. Garfield; 1831 ? 1881)1881 年成为美国第 20 任总统
1876 年提出有关证明证明二及证明三的比较两个证明基本上相同! 证明二及证明三的“缺点”两个证明都需要到以下恒等式:
(a ? b)2 = a2 ? 2ab + b2 a2b2证明四证明四证明四证明四证明四c2? a2 + b2 = c2出入相补 刘徽(生于公元三世纪) 三国魏晋时代人。
魏景元四年(即 263 年)为古籍《九章算术》作注释。
在注作中,提出以「出入相补」的原理来证明「勾股定理」。后人称该图为「青朱入出图」。
拼图游戏拼图游戏证明五c2证明五证明五证明五a2b2? a2 + b2 = c2无字证明 sin(a + b) = sin a cos b + sin b cos a印度婆什迦罗的证明 ? c2 = b2 + a2证明六注意:
面积I : 面积 II : 面积 III = a2 : b2 : c2 证明六IIIIII注意:
面积I : 面积 II : 面积 III = a2 : b2 : c2 证明六IIIIII注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2 证明六注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2 证明六注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2 证明六注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2 证明六注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2 由此得,面积 I + 面积 II = 面积 III
因此,a2 + b2 = c2 。
? 欧几里得的《几何原本》是用公理方法建立演绎数学体系的最早典范。
“证明一”就是取材自《几何原本》第一卷的第 47 命题。证明二ba (a + b)2 = c2 + 4( ab)
a2 + 2ab + b2 = c2 + 2ab
? a2 + b2 = c2c证明二cb ? a c2 = (a ? b)2 + 4( ab)
= a2 ? 2ab + b2 + 2ab
? c2 = a2 + b2弦图 ?赵爽
?东汉末至三国时代吴国人
?为《周髀算经》作注,并着有《勾股圆方图说》。 证明三 (a + b)(b + a) = c2 + 2( ab)
a2 + ab + b2 = c2 + ab
? a2 + b2 = c2aabbcc美国总统的证明加菲尔德(James A. Garfield; 1831 ? 1881)1881 年成为美国第 20 任总统
1876 年提出有关证明证明二及证明三的比较两个证明基本上相同! 证明二及证明三的“缺点”两个证明都需要到以下恒等式:
(a ? b)2 = a2 ? 2ab + b2 a2b2证明四证明四证明四证明四证明四c2? a2 + b2 = c2出入相补 刘徽(生于公元三世纪) 三国魏晋时代人。
魏景元四年(即 263 年)为古籍《九章算术》作注释。
在注作中,提出以「出入相补」的原理来证明「勾股定理」。后人称该图为「青朱入出图」。
拼图游戏拼图游戏证明五c2证明五证明五证明五a2b2? a2 + b2 = c2无字证明 sin(a + b) = sin a cos b + sin b cos a印度婆什迦罗的证明 ? c2 = b2 + a2证明六注意:
面积I : 面积 II : 面积 III = a2 : b2 : c2 证明六IIIIII注意:
面积I : 面积 II : 面积 III = a2 : b2 : c2 证明六IIIIII注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2 证明六注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2 证明六注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2 证明六注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2 证明六注意:
面积 I : 面积 II : 面积 III = a2 : b2 : c2 由此得,面积 I + 面积 II = 面积 III
因此,a2 + b2 = c2 。
