27.3 位似同步课件
图片预览









文档简介
课件35张PPT。第二十七章
位 似27.3
位 似 新知1 位似图形
1. 位似图形:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么像这样的两个图形叫做位似图形,这个点叫做位似中心.
2. 位似图形的性质:每一组对应点和位似中心在同一直线上,它们到位似中心的距离之比都等于相似比.
3. 由一个图形得到它的位似图形的变换叫做位似变换.利用位似变换可以把一个图形放大或缩小. 【例1】下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于相似比.其中正确命题的序号是( )
A. ②③ B. ①② C. ③④ D. ②③④ 例题精讲 解析 ①相似图形不一定是位似图形,位似图形一定是相似图形,故此命题错误;②位似图形一定有位似中心,此命题正确;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形,此命题正确;④位似图形上对应(不是任意)两点与位似中心的距离之比等于相似比,此命题错误.正确的命题为②③.
答案 A 1. 下列说法正确的是( )
A. 对角线互相平分的四边形是矩形
B. 平行四边形是轴对称图形
C. 位似三角形是相似三角形
D. 可以选用同一种正五边形图形镶嵌地面 举一反三C 2. 下列说法错误的是( )
A. 位似图形的对应点和位似中心在同一条直线上
B. 位似图形上任意一对对应点到位似中心的距离之比等于位似比
C. 位似图形一定是相似图形
D. 位似图形的对应线段不可能在同一条直线上D 新知2 位似图形的性质
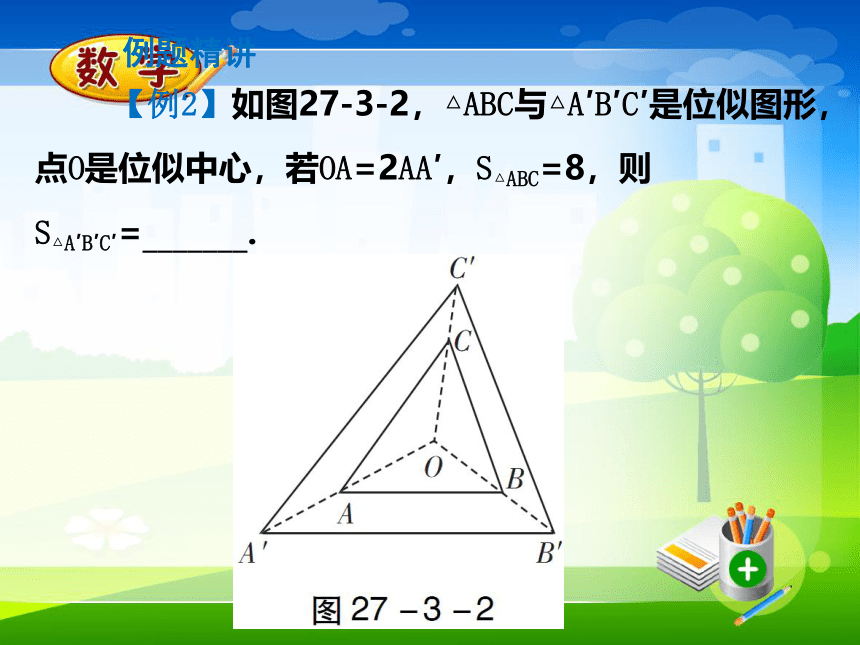
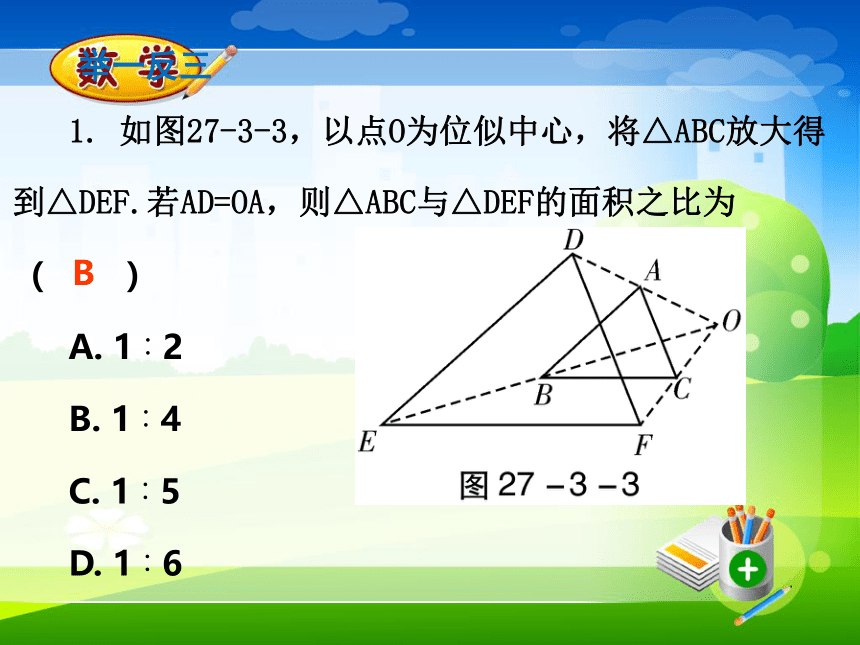
一般性质(具有相似多边形的性质):周长比等于相似比;面积比等于相似比的平方.特殊性质:位似图形上任意一组对应顶点到位似中心的距离之比等于相似比. 【例2】如图27-3-2,△ABC与△A′B′C′是位似图形,点O是位似中心,若OA=2AA′,S△ABC=8,则S△A′B′C′=_______. 例题精讲 1. 如图27-3-3,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA,则△ABC与△DEF的面积之比为( )
A. 1∶2
B. 1∶4
C. 1∶5
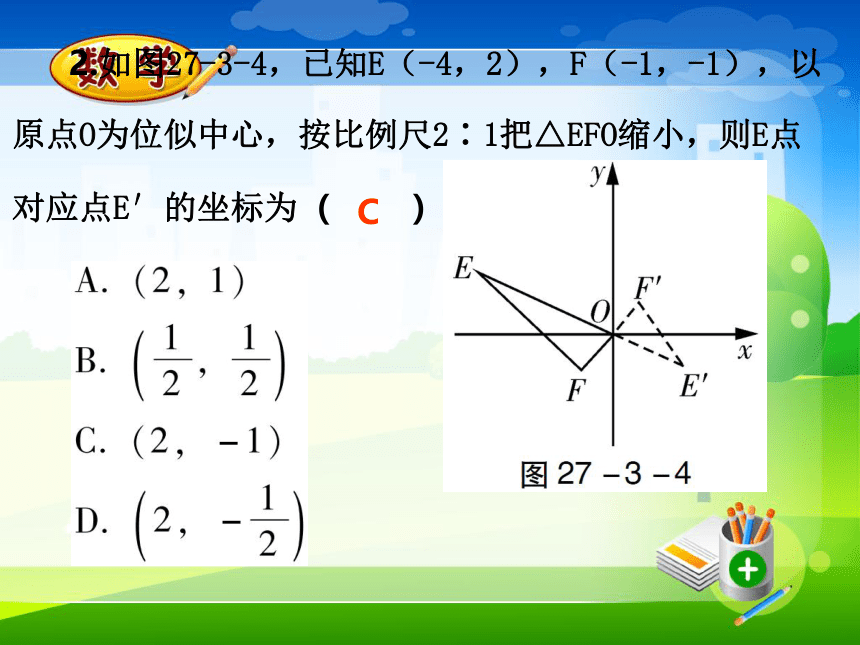
D. 1∶6 举一反三B 2.如图27-3-4,已知E(-4,2),F(-1,-1),以原点O为位似中心,按比例尺2∶1把△EFO缩小,则E点对应点E′的坐标为( )C 新知3 作位似图形
画位似图形的步骤:(1)确定位似中心;(2)确定原图的关键点;(3)确定相似比;(4)找出新图形的对应关键点;(4)画出图形. 【例3】如图27-3-5,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6). 例题精讲 (1)画出△ABC,并画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1;
(2)以原点O为位似中心,画出将△A1B1C1的三条边放大为原来2倍后的△A2B2C2.
解析 (1)由A(-1,2),B(-3,4),C(-2,6),可画出△ABC,然后由旋转的性质,即可画出△A1B1C1;
(2)由位似三角形的性质,即可画出△A2B2C2. 解 (1)如图27-3-6:(1)△ABC和△A1B1C1即为所求;(2)△A2B2C2 即为所求. 1. 如图27-3-7,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3). 举一反三 (1)画出△ABC关于x轴对称的△A1B1C1;
(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1的相似比为2∶1. 解:如答图27-3-1所示. 新知4 用坐标描述位似变换
在平面直角坐标系中,以原点O为位似中心,相似比为k,若原图形上点A的坐标为(x,y),那么位似图形对应点A′的坐标为(kx,ky)或(-kx,-ky). 【例4】如图27-3-8,△ABC三个定点的坐标分别为A(-1,3),B(-1,1),C(-3,2).
(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2,请在第三象限内画出△A2B2C2,并求出 的值. 例题精讲 解析 (1)根据网格结构找出点A,B,C关于y轴的对称点A1,B1,C1的位置,然后顺次连接即可;
(2)连接A1O并延长至A2,使A2O=2A1O,连接B1O并延长至B2,使B2O=2B1O,连接C1O并延长至C2,使C2O=2C1O,然后顺次连接即可,再根据相似三角形的面积比等于相似比的平方求出面积比. 解 (1)△A1B1C1如图27-3-9所示. 1. 如图27-3-10,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网络线的交点)和点O,按要求画出四边形A1B1C1D1和四边形A2B2C2D2.
(1)将四边形ABCD绕O点顺时针旋转90°,得到四边形A1B1C1D1;
(2)以O点为位似中心,在异侧作位似变换,且使四边形ABCD的面积扩大为原来的4倍,得到四边形A2B2C2D2. 举一反三 解:(1)如答图27-3-2所示:四边形A1B1C1D1即为所求.
(2)如答图27-3-2所示:四边形A2B2C2D2即为所求. 1. 位似图形的定义:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,像这样的两个图形叫做位似图形,这个点叫做位似中心.
2. 位似图形的性质:除了具有相似多边形的全部性质外,还具有的特殊性质——位似图形上任意一组对应顶点到位似中心的距离之比等于相似比. 方法规律 7. (6分)如图KT27-3-3,在边长均为1的小正方形网格纸中,△OAB的顶点O,A,B均在格点上,且O是直角坐标系的原点,点A在x轴上. (1)以O为位似中心将△OAB放大,使得放大后的△OA1B1与△OAB对应线段的比为2∶1,画出△OA1B1(所画△OA1B1与△OAB在原点两侧);
(2)求出线段A1B1所在直线的函数关系式. 解:(1)如答图27-3-3,△OA1B1就是△OAB放大后的图象. 8. (6分)已知图KT27-3-4,请作出一个新图形,使新图形与原图形的位似比为2∶1. 解:作法如下:①取关键点A,B,C,D,在图外取点P,作射线AP,BP,CP,DP;
②在它们上面分别取A′,B′,
C,′D′,使得PA′=2PA,PB′=
2PB,PC′=2PC,PD′=2PD.
③顺次连接A′,B′,C′,D′,
四边形A′B′C′D′即为所求.
如答图27-3-4.
位 似27.3
位 似 新知1 位似图形
1. 位似图形:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么像这样的两个图形叫做位似图形,这个点叫做位似中心.
2. 位似图形的性质:每一组对应点和位似中心在同一直线上,它们到位似中心的距离之比都等于相似比.
3. 由一个图形得到它的位似图形的变换叫做位似变换.利用位似变换可以把一个图形放大或缩小. 【例1】下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于相似比.其中正确命题的序号是( )
A. ②③ B. ①② C. ③④ D. ②③④ 例题精讲 解析 ①相似图形不一定是位似图形,位似图形一定是相似图形,故此命题错误;②位似图形一定有位似中心,此命题正确;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形,此命题正确;④位似图形上对应(不是任意)两点与位似中心的距离之比等于相似比,此命题错误.正确的命题为②③.
答案 A 1. 下列说法正确的是( )
A. 对角线互相平分的四边形是矩形
B. 平行四边形是轴对称图形
C. 位似三角形是相似三角形
D. 可以选用同一种正五边形图形镶嵌地面 举一反三C 2. 下列说法错误的是( )
A. 位似图形的对应点和位似中心在同一条直线上
B. 位似图形上任意一对对应点到位似中心的距离之比等于位似比
C. 位似图形一定是相似图形
D. 位似图形的对应线段不可能在同一条直线上D 新知2 位似图形的性质
一般性质(具有相似多边形的性质):周长比等于相似比;面积比等于相似比的平方.特殊性质:位似图形上任意一组对应顶点到位似中心的距离之比等于相似比. 【例2】如图27-3-2,△ABC与△A′B′C′是位似图形,点O是位似中心,若OA=2AA′,S△ABC=8,则S△A′B′C′=_______. 例题精讲 1. 如图27-3-3,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA,则△ABC与△DEF的面积之比为( )
A. 1∶2
B. 1∶4
C. 1∶5
D. 1∶6 举一反三B 2.如图27-3-4,已知E(-4,2),F(-1,-1),以原点O为位似中心,按比例尺2∶1把△EFO缩小,则E点对应点E′的坐标为( )C 新知3 作位似图形
画位似图形的步骤:(1)确定位似中心;(2)确定原图的关键点;(3)确定相似比;(4)找出新图形的对应关键点;(4)画出图形. 【例3】如图27-3-5,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6). 例题精讲 (1)画出△ABC,并画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1;
(2)以原点O为位似中心,画出将△A1B1C1的三条边放大为原来2倍后的△A2B2C2.
解析 (1)由A(-1,2),B(-3,4),C(-2,6),可画出△ABC,然后由旋转的性质,即可画出△A1B1C1;
(2)由位似三角形的性质,即可画出△A2B2C2. 解 (1)如图27-3-6:(1)△ABC和△A1B1C1即为所求;(2)△A2B2C2 即为所求. 1. 如图27-3-7,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3). 举一反三 (1)画出△ABC关于x轴对称的△A1B1C1;
(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1的相似比为2∶1. 解:如答图27-3-1所示. 新知4 用坐标描述位似变换
在平面直角坐标系中,以原点O为位似中心,相似比为k,若原图形上点A的坐标为(x,y),那么位似图形对应点A′的坐标为(kx,ky)或(-kx,-ky). 【例4】如图27-3-8,△ABC三个定点的坐标分别为A(-1,3),B(-1,1),C(-3,2).
(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2,请在第三象限内画出△A2B2C2,并求出 的值. 例题精讲 解析 (1)根据网格结构找出点A,B,C关于y轴的对称点A1,B1,C1的位置,然后顺次连接即可;
(2)连接A1O并延长至A2,使A2O=2A1O,连接B1O并延长至B2,使B2O=2B1O,连接C1O并延长至C2,使C2O=2C1O,然后顺次连接即可,再根据相似三角形的面积比等于相似比的平方求出面积比. 解 (1)△A1B1C1如图27-3-9所示. 1. 如图27-3-10,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网络线的交点)和点O,按要求画出四边形A1B1C1D1和四边形A2B2C2D2.
(1)将四边形ABCD绕O点顺时针旋转90°,得到四边形A1B1C1D1;
(2)以O点为位似中心,在异侧作位似变换,且使四边形ABCD的面积扩大为原来的4倍,得到四边形A2B2C2D2. 举一反三 解:(1)如答图27-3-2所示:四边形A1B1C1D1即为所求.
(2)如答图27-3-2所示:四边形A2B2C2D2即为所求. 1. 位似图形的定义:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,像这样的两个图形叫做位似图形,这个点叫做位似中心.
2. 位似图形的性质:除了具有相似多边形的全部性质外,还具有的特殊性质——位似图形上任意一组对应顶点到位似中心的距离之比等于相似比. 方法规律 7. (6分)如图KT27-3-3,在边长均为1的小正方形网格纸中,△OAB的顶点O,A,B均在格点上,且O是直角坐标系的原点,点A在x轴上. (1)以O为位似中心将△OAB放大,使得放大后的△OA1B1与△OAB对应线段的比为2∶1,画出△OA1B1(所画△OA1B1与△OAB在原点两侧);
(2)求出线段A1B1所在直线的函数关系式. 解:(1)如答图27-3-3,△OA1B1就是△OAB放大后的图象. 8. (6分)已知图KT27-3-4,请作出一个新图形,使新图形与原图形的位似比为2∶1. 解:作法如下:①取关键点A,B,C,D,在图外取点P,作射线AP,BP,CP,DP;
②在它们上面分别取A′,B′,
C,′D′,使得PA′=2PA,PB′=
2PB,PC′=2PC,PD′=2PD.
③顺次连接A′,B′,C′,D′,
四边形A′B′C′D′即为所求.
如答图27-3-4.
