江苏省无锡市堰桥高级中学高中数学必修一教学课件:用二分法求方程的近似解 (共21张PPT)
文档属性
| 名称 | 江苏省无锡市堰桥高级中学高中数学必修一教学课件:用二分法求方程的近似解 (共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 253.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-17 10:46:58 | ||
图片预览








文档简介
课件21张PPT。用二分法求方程的近似解从上海到美国旧金山的海底电缆有15个接点,现在某接点
发生故障,需及时修理,为了尽快断定故障发生点,一般
至少需要检查接点的个数为 个。请你思考A B C D E F G H I J K L M N O问题2算一算:查找线路电线、水管、气管等管道线路故障定义:每次取中点,将区间一分为二,再经比较,
按需要留下其中一个小区间的方法叫二分法,
也叫对分法,常用于: 在一个风雨交加的夜里,从某水库闸房
到防洪指挥部的电话线路发生了故障,这上一
条10km长的线路,如何迅速查出故障所在? 要把故障可能发生的范围缩小到
50~100m左右,即一两根电线杆附近,
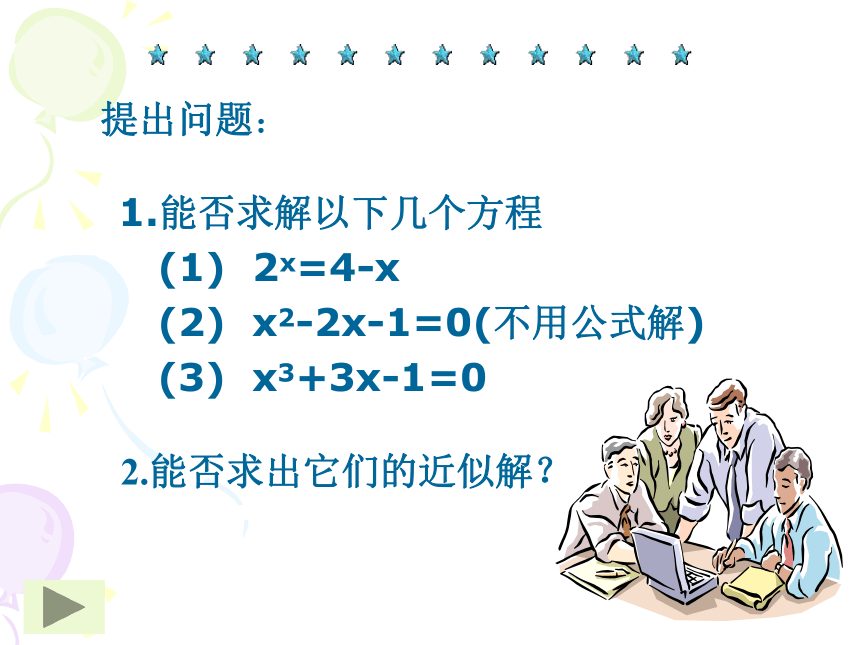
要检查多少次?方法分析:实验设计、资料查询;是方程求根的常用方法!7次 1.能否求解以下几个方程
(1) 2x=4-x
(2) x2-2x-1=0(不用公式解)
(3) x3+3x-1=0
提出问题:2.能否求出它们的近似解?3.什么方法?4.能否找到其它的方法,使解更精确?探究解法(1)不解方程,如何求方程x2-2x-1=0的一个正的近似解(精确到0.1)?
方法:引出借助函数f(x)= x2-2x-1的图象,能够缩小根所在的区间,并根据f(2)<0,f(3)>0,可得出根所在区间为(2,3).指出:用配方法求得方程的解,但此法不能运用于解另外两个方程。如何求方程 x2-2x-1=0 的一个正的近似解 .
(精确到0.1)方法探究(2)能否简述上述求方程近似解的过程?(3)二分法(bisection method):象上面这种求方程近似解的方法称为二分法,它是求一元方程近似解的常用方法。
定义如下:
对于区间[a,b]上连续不断、且f(a)f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection)
自行探究利用计算器,求方程 lgx=3 - x的近似解.(精确到0.1)解:画出y=lg x及y=3 -x的图象,观察图象得,方程lgx=3 - x有唯一解,记为x,且这个解在区间(2,3)内。设 f (x)=lgx+x -3 因为2.5625,2.625精确到0.1的近似值都为2.6,所以原方程的
近似解为x1≈2.6 .(2,3)f(2)<0,f(3)>02.5f(2.5)<0(2.5,3)f(2.5)<0,f(3)>02.75f(2.75)>0(2.5,2.75)f(2.5)<0,f(2.75)>02.625f(2.625)>0(2.5,2.625)f(2.5)<0,f(2.625)>02.5625f(2.5625)<0(2.5625,2.625)f(2.5625)<0,f(2.625)>0例题处理求函数 在区间(2,3)内的零点.解答方式列表:归纳总结用二分法求方程 f(x)=0(或g(x)=h(x))近似解的基本步骤:1、寻找解所在区间(1)图象法先画出y= f(x)图象,观察图象与x轴的交点横坐标所处的范围;或画出y=g(x)和y=h(x)的图象,观察两图象的交点横坐标的范围。(2)函数法把方程均转换为 f(x)=0的形式,再利用函数y=f(x)的有关性质(如单调性)来判断解所在的区间。2、不断二分解所在的区间对(1)、(2)两种情形再继续二分解所在的区间.3、根据精确度得出近似解求方程x3+3x-1=0的一个近似解。(精确到0.1)画y=x3+3x-1的图象比较困难,变形为x3=1-3x,画两个函数的图象如何?练习:解:令f(x)=x3+3x-1, 有f(0)<0,f(1)>0,则方程的解在 0,1之间。(0,1)f(0)<0,f(1)>00.5f(0.5)>0(0,0.5)(0.25,0.5)(0.25,0.375)(0.25,0.3125)f(0)<0,f(0.5)>0f(0.25)<0,f(0.5)>0f(0.25)<0,f(0.375)>00.25f(0.25)<00.375f(0.375)>00.3125f(0.3125)<0课堂小结1.引导学生回顾二分法,明确它是一种求一元方程近似解的通法。
2.揭示算法定义,了解算法特点。
算法:如果一种计算方法对某一类问(不是个别问题)都有效,计算可以一步一步地进行,每一步都能得到惟一的结果,我们常把这一类问题的求解过程叫做解决这一类问题的一种算法。
课堂小结
算法特点:算法是刻板的、机械的,有时要进行大量的重复计算,但它的优点是一种通法,只要按部就班地去做,总会算出结果。更大的优点是它可以让计算机来实现。
3.鼓励学生尝试通过计算机来求方程的近似解。 谢谢大家, 请批评指正! 问题3师评
发生故障,需及时修理,为了尽快断定故障发生点,一般
至少需要检查接点的个数为 个。请你思考A B C D E F G H I J K L M N O问题2算一算:查找线路电线、水管、气管等管道线路故障定义:每次取中点,将区间一分为二,再经比较,
按需要留下其中一个小区间的方法叫二分法,
也叫对分法,常用于: 在一个风雨交加的夜里,从某水库闸房
到防洪指挥部的电话线路发生了故障,这上一
条10km长的线路,如何迅速查出故障所在? 要把故障可能发生的范围缩小到
50~100m左右,即一两根电线杆附近,
要检查多少次?方法分析:实验设计、资料查询;是方程求根的常用方法!7次 1.能否求解以下几个方程
(1) 2x=4-x
(2) x2-2x-1=0(不用公式解)
(3) x3+3x-1=0
提出问题:2.能否求出它们的近似解?3.什么方法?4.能否找到其它的方法,使解更精确?探究解法(1)不解方程,如何求方程x2-2x-1=0的一个正的近似解(精确到0.1)?
方法:引出借助函数f(x)= x2-2x-1的图象,能够缩小根所在的区间,并根据f(2)<0,f(3)>0,可得出根所在区间为(2,3).指出:用配方法求得方程的解,但此法不能运用于解另外两个方程。如何求方程 x2-2x-1=0 的一个正的近似解 .
(精确到0.1)方法探究(2)能否简述上述求方程近似解的过程?(3)二分法(bisection method):象上面这种求方程近似解的方法称为二分法,它是求一元方程近似解的常用方法。
定义如下:
对于区间[a,b]上连续不断、且f(a)f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection)
自行探究利用计算器,求方程 lgx=3 - x的近似解.(精确到0.1)解:画出y=lg x及y=3 -x的图象,观察图象得,方程lgx=3 - x有唯一解,记为x,且这个解在区间(2,3)内。设 f (x)=lgx+x -3 因为2.5625,2.625精确到0.1的近似值都为2.6,所以原方程的
近似解为x1≈2.6 .(2,3)f(2)<0,f(3)>02.5f(2.5)<0(2.5,3)f(2.5)<0,f(3)>02.75f(2.75)>0(2.5,2.75)f(2.5)<0,f(2.75)>02.625f(2.625)>0(2.5,2.625)f(2.5)<0,f(2.625)>02.5625f(2.5625)<0(2.5625,2.625)f(2.5625)<0,f(2.625)>0例题处理求函数 在区间(2,3)内的零点.解答方式列表:归纳总结用二分法求方程 f(x)=0(或g(x)=h(x))近似解的基本步骤:1、寻找解所在区间(1)图象法先画出y= f(x)图象,观察图象与x轴的交点横坐标所处的范围;或画出y=g(x)和y=h(x)的图象,观察两图象的交点横坐标的范围。(2)函数法把方程均转换为 f(x)=0的形式,再利用函数y=f(x)的有关性质(如单调性)来判断解所在的区间。2、不断二分解所在的区间对(1)、(2)两种情形再继续二分解所在的区间.3、根据精确度得出近似解求方程x3+3x-1=0的一个近似解。(精确到0.1)画y=x3+3x-1的图象比较困难,变形为x3=1-3x,画两个函数的图象如何?练习:解:令f(x)=x3+3x-1, 有f(0)<0,f(1)>0,则方程的解在 0,1之间。(0,1)f(0)<0,f(1)>00.5f(0.5)>0(0,0.5)(0.25,0.5)(0.25,0.375)(0.25,0.3125)f(0)<0,f(0.5)>0f(0.25)<0,f(0.5)>0f(0.25)<0,f(0.375)>00.25f(0.25)<00.375f(0.375)>00.3125f(0.3125)<0课堂小结1.引导学生回顾二分法,明确它是一种求一元方程近似解的通法。
2.揭示算法定义,了解算法特点。
算法:如果一种计算方法对某一类问(不是个别问题)都有效,计算可以一步一步地进行,每一步都能得到惟一的结果,我们常把这一类问题的求解过程叫做解决这一类问题的一种算法。
课堂小结
算法特点:算法是刻板的、机械的,有时要进行大量的重复计算,但它的优点是一种通法,只要按部就班地去做,总会算出结果。更大的优点是它可以让计算机来实现。
3.鼓励学生尝试通过计算机来求方程的近似解。 谢谢大家, 请批评指正! 问题3师评
