福建省晋江市季延中学人教版高中数学必修一课件:1.3函数的奇偶性 (共29张PPT)
文档属性
| 名称 | 福建省晋江市季延中学人教版高中数学必修一课件:1.3函数的奇偶性 (共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 615.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-18 09:13:18 | ||
图片预览





文档简介
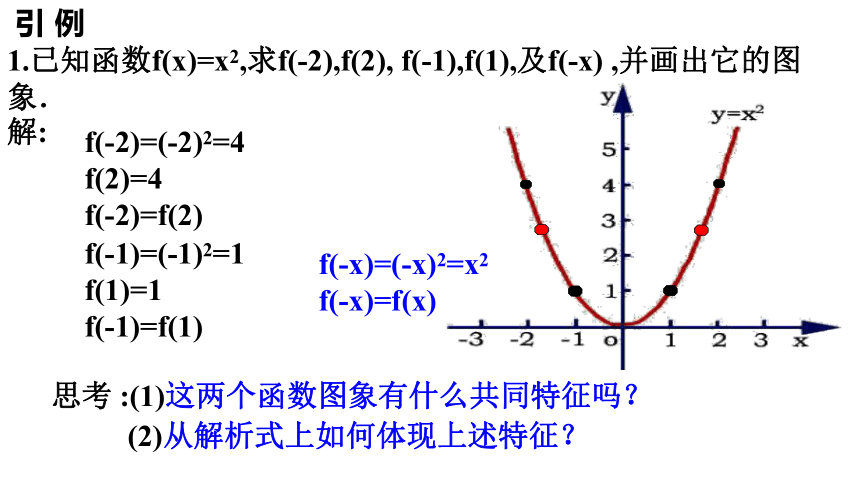
课件29张PPT。函数的奇偶性引 例1.已知函数f(x)=x2,求f(-2),f(2), f(-1),f(1),及f(-x) ,并画出它的图象.解:f(-2)=(-2)2=4 f(2)=4
f(-2)=f(2)f(-1)=(-1)2=1 f(1)=1
f(-1)=f(1)f(-x)=(-x)2=x2
f(-x)=f(x)思考 :(1)这两个函数图象有什么共同特征吗?
(2)从解析式上如何体现上述特征?偶函数的特征:①解析式的基本特征:f (-x)=f (x)②图像特征:关于y轴对称. 如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数(even fun_ction).1. 偶函数的概念
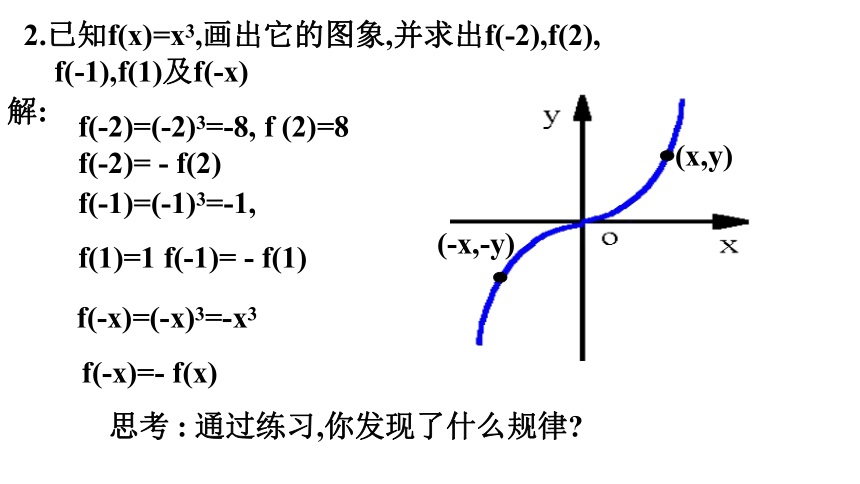
2.已知f(x)=x3,画出它的图象,并求出f(-2),f(2),
f(-1),f(1)及f(-x)解:f(-2)=(-2)3=-8, f (2)=8
f(-2)= - f(2)f(-1)=(-1)3=-1,
f(1)=1 f(-1)= - f(1)f(-x)=(-x)3=-x3
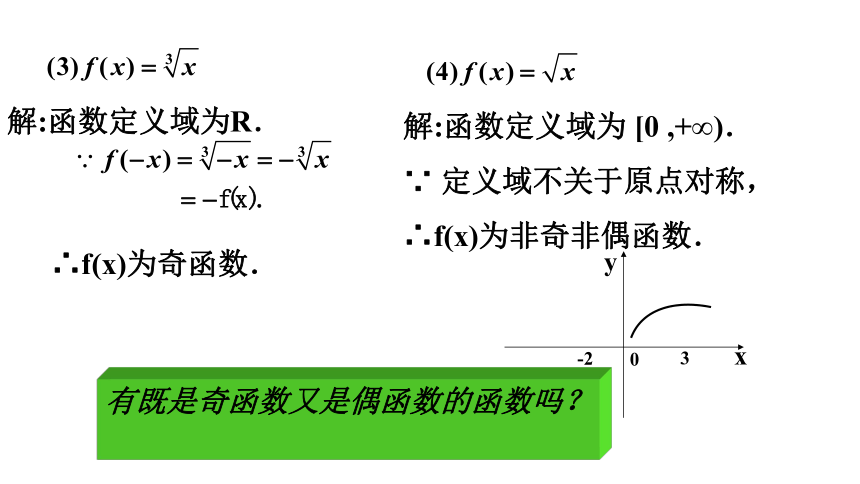
f(-x)=- f(x)思考 : 通过练习,你发现了什么规律?(-x,-y)(x,y)奇函数的特征:①解析式的基本特征:f (-x)=-f (x)②图像特征:关于原点对称. 如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数(odd fun_ction).2.奇函数的概念 如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.(1)奇、偶函数定义的逆命题也成立,即若f(x)为奇函数, 则f(-x)=-f(x)成立.若f(x)为偶函数, 则f(-x)= f(x) 成立.(2)判断函数是否具有奇偶性.首先要看函数的定义域是否关于原点对称,即函数定义域关于原点对称是函数具有奇偶性的前提.注意事项(3)函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;而函数的单调性是函数的局部性质.例1. 判断下列函数的奇偶性(1) f(x)=x3+2x; (2) f(x)=2x4+3x2;解:∵f(-x)=(-x)3+2(-x)= -x3-2x= -(x3+2x)= - f(x),∴f(x)为奇函数. ∵f(-x)=2(-x)4+3(-x)2=2x4+3x2∴f(x)为偶函数.函数定义域为R.解:函数定义域为R.= f(x),解:函数定义域为R.∴f(x)为奇函数.有既是奇函数又是偶函数的函数吗?解:函数定义域为 [0 ,+∞).
∵ 定义域不关于原点对称,
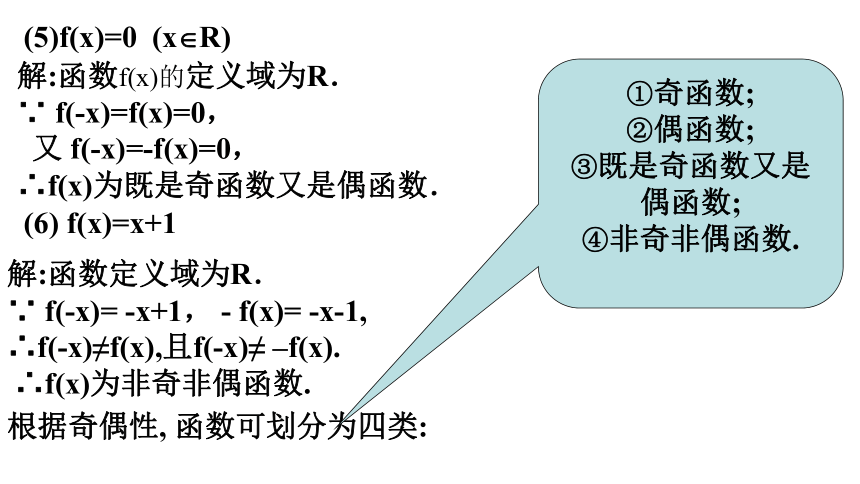
∴f(x)为非奇非偶函数.(6) f(x)=x+1解:函数f(x)的定义域为R.
∵ f(-x)=f(x)=0,
又 f(-x)=-f(x)=0,
∴f(x)为既是奇函数又是偶函数.(5)f(x)=0 (x?R)根据奇偶性, 函数可划分为四类:①奇函数;
②偶函数;
③既是奇函数又是偶函数;
④非奇非偶函数.
解:函数定义域为R.
∵ f(-x)= -x+1, - f(x)= -x-1,
∴f(-x)≠f(x),且f(-x)≠ –f(x).
∴f(x)为非奇非偶函数.判定函数的奇偶性的步骤:
(1)先求函数的定义域;
①若定义域不是关于原点对称的区间,则函数为非奇非偶函数.
②若定义域是关于原点对称的区间,进入第二步;
(2)计算f(-x)化向 f ( x ) 的解析式;
①若等于 f ( x ),则函数是偶函数,
②若等于-f ( x ),则函数是奇函数,
③若不等于 ,则函数是非奇非偶函数
(3)结论.有时判定f(-x)=±f(x)比较困难,可考虑判定f(-x)±f(x)=0或判定f(x)/f(-x)=±1. 练习:判断下列函数的奇偶性∴f(x)为奇函数.解:定义域为{x|x≠0},即 f(-x)= - f(x),(2)f(x)=5解:f(x)的定义域为R.
∵ f(-x)=f(x)=5∴f(x)为偶函数.(4)f(x)=|x+1|-|x-1|∴f(x)既是偶函数, 又是奇函数. 解:函数的定义域为{-1,1},解:f(x)的定义域为R∵ f(-x)= |-x+1|-|-x-1|= |x-1|-|x+1|∴f(-x)=-f(x)∴f(x)为奇函数.例2.若函数
是偶函数,求m的值. 【1】已知函数f(x)=ax2+bx+c,(2a-3≤x≤1)是偶函数,则a=___,b=____,c∈___.10R【2】对于奇函数f(x),若x能取到零,则f(0)=__. 0函数 是偶函数. 【3】对于定义在R上的函数 f (x),下列判断是否正确?若f (-2) = f (2),则函数 f (x)是偶函数.若f (-2)≠f (2),则函数 f (x)不是偶函数.练一练 例3.已知函数y=f(x) 在R上是奇函数,而且在(0,+∞)上是增函数,证明y=f(x)在(-∞,0)上也是增函数. 证明:任取x1, x2∈(-∞,0),且x1-x2>0,∵f(x)在(0,+∞)上是减函数,∴ f(-x1 )< f(-x2 ).∵ f(x) 是偶函数,∴ f(x1) < f(x2).故f(x)在(-∞,0)上是增函数. 已知函数y=f(x) 在R上是偶函数,而且在(0,+∞)上是减函数,那么y=f(x)在(-∞,0)上是增函数还是减函数?想一想练一练 【1】已知函数 f(x) 是奇函数,当 x≥0时,
f(x)=x(1+x); 当 x < 0 时, f(x)等于 ( ).B 【2】已知 f(x) 是定义在R上的奇函数,当x>0时, f(x)=x2+x-1, 求函数f(x)的表达式.引申:如果改为偶函数呢?一、奇函数、偶函数的图象性质1.奇函数的图象关于原点成中心对称图形;2.偶函数的图象关于y 轴成轴对称图形.奇偶函数图象的性质可用于:
①简化函数图象的画法;
②判断函数的奇偶性.例题讲解 例1. 已知函数y=f(x)是偶函数,它在y轴右边的图象如图,画出y=f(x)在 y轴左边的图象.解:画法略(一)简化函数图象的画法【1】作出函数 y=x2 -2|x|-3 的图象.-31-1练一练点评:用对称法作图时,先作出 x≥0的图象,由函数是偶函数,再用对称法作出另一半的图象.【2】如果奇函数f(x)在区间[3,7]上为增函数,且最小值是5,则在区间[-7,-3]上有没有最大值?是多少?解:如图所示函数有最大值 函数f(x)在区间[-7,-3]上为增函数.【3】已知f(x)是偶函数,g(x)是奇函数,
试将下图补充完整。【4】判断下列函数的奇偶性:
(非奇非偶函数)(奇函数)0............(偶函数)【5】已知f(x)=x5+bx3+cx且f(-2)=10,那么f(2)等于( )。
A、-10 B、10 C、20 D、与b、c有关
【6】下面四个命题中,正确的个数是( )
①奇函数的图像关于原点对称。
②偶函数的图像关于y轴对称。
③奇函数的图像一定过原点。
④偶函数的图像一定与y轴相交。
A、4 B、3 C、2 D、1
【7】如果定义在[3-a,5]上的函数f(x)为奇函数,那么,
a= ________ AC82-2思考你能画出f(x)的大致图像吗 ?答案:课堂小结1.函数奇偶性的定义. 定义法利用性质2.函数奇偶性的判定图象法:画出函数图象①考查函数定义域是否关于原点对称;
②判断f(-x)=±f(x)之一是否成立;
③作出结论.一个函数为奇函数?它的图象关于原点对称.一个函数为偶函数?它的图象关于y 轴对称.3.性质: 奇函数在关于原点对称的区间上具有相同的单调性;偶函数在关于原点对称的区间上具有相反的单调性.(2)在定义域的关于原点对称的公共区间内奇±奇=奇;偶±偶=偶;奇±偶=非奇非偶.偶×偶=偶;奇×奇=偶;偶×奇=奇.(1)奇函数、偶函数的图象特点(3)奇偶性与单调性的关系
f(-2)=f(2)f(-1)=(-1)2=1 f(1)=1
f(-1)=f(1)f(-x)=(-x)2=x2
f(-x)=f(x)思考 :(1)这两个函数图象有什么共同特征吗?
(2)从解析式上如何体现上述特征?偶函数的特征:①解析式的基本特征:f (-x)=f (x)②图像特征:关于y轴对称. 如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数(even fun_ction).1. 偶函数的概念
2.已知f(x)=x3,画出它的图象,并求出f(-2),f(2),
f(-1),f(1)及f(-x)解:f(-2)=(-2)3=-8, f (2)=8
f(-2)= - f(2)f(-1)=(-1)3=-1,
f(1)=1 f(-1)= - f(1)f(-x)=(-x)3=-x3
f(-x)=- f(x)思考 : 通过练习,你发现了什么规律?(-x,-y)(x,y)奇函数的特征:①解析式的基本特征:f (-x)=-f (x)②图像特征:关于原点对称. 如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数(odd fun_ction).2.奇函数的概念 如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.(1)奇、偶函数定义的逆命题也成立,即若f(x)为奇函数, 则f(-x)=-f(x)成立.若f(x)为偶函数, 则f(-x)= f(x) 成立.(2)判断函数是否具有奇偶性.首先要看函数的定义域是否关于原点对称,即函数定义域关于原点对称是函数具有奇偶性的前提.注意事项(3)函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;而函数的单调性是函数的局部性质.例1. 判断下列函数的奇偶性(1) f(x)=x3+2x; (2) f(x)=2x4+3x2;解:∵f(-x)=(-x)3+2(-x)= -x3-2x= -(x3+2x)= - f(x),∴f(x)为奇函数. ∵f(-x)=2(-x)4+3(-x)2=2x4+3x2∴f(x)为偶函数.函数定义域为R.解:函数定义域为R.= f(x),解:函数定义域为R.∴f(x)为奇函数.有既是奇函数又是偶函数的函数吗?解:函数定义域为 [0 ,+∞).
∵ 定义域不关于原点对称,
∴f(x)为非奇非偶函数.(6) f(x)=x+1解:函数f(x)的定义域为R.
∵ f(-x)=f(x)=0,
又 f(-x)=-f(x)=0,
∴f(x)为既是奇函数又是偶函数.(5)f(x)=0 (x?R)根据奇偶性, 函数可划分为四类:①奇函数;
②偶函数;
③既是奇函数又是偶函数;
④非奇非偶函数.
解:函数定义域为R.
∵ f(-x)= -x+1, - f(x)= -x-1,
∴f(-x)≠f(x),且f(-x)≠ –f(x).
∴f(x)为非奇非偶函数.判定函数的奇偶性的步骤:
(1)先求函数的定义域;
①若定义域不是关于原点对称的区间,则函数为非奇非偶函数.
②若定义域是关于原点对称的区间,进入第二步;
(2)计算f(-x)化向 f ( x ) 的解析式;
①若等于 f ( x ),则函数是偶函数,
②若等于-f ( x ),则函数是奇函数,
③若不等于 ,则函数是非奇非偶函数
(3)结论.有时判定f(-x)=±f(x)比较困难,可考虑判定f(-x)±f(x)=0或判定f(x)/f(-x)=±1. 练习:判断下列函数的奇偶性∴f(x)为奇函数.解:定义域为{x|x≠0},即 f(-x)= - f(x),(2)f(x)=5解:f(x)的定义域为R.
∵ f(-x)=f(x)=5∴f(x)为偶函数.(4)f(x)=|x+1|-|x-1|∴f(x)既是偶函数, 又是奇函数. 解:函数的定义域为{-1,1},解:f(x)的定义域为R∵ f(-x)= |-x+1|-|-x-1|= |x-1|-|x+1|∴f(-x)=-f(x)∴f(x)为奇函数.例2.若函数
是偶函数,求m的值. 【1】已知函数f(x)=ax2+bx+c,(2a-3≤x≤1)是偶函数,则a=___,b=____,c∈___.10R【2】对于奇函数f(x),若x能取到零,则f(0)=__. 0函数 是偶函数. 【3】对于定义在R上的函数 f (x),下列判断是否正确?若f (-2) = f (2),则函数 f (x)是偶函数.若f (-2)≠f (2),则函数 f (x)不是偶函数.练一练 例3.已知函数y=f(x) 在R上是奇函数,而且在(0,+∞)上是增函数,证明y=f(x)在(-∞,0)上也是增函数. 证明:任取x1, x2∈(-∞,0),且x1
f(x)=x(1+x); 当 x < 0 时, f(x)等于 ( ).B 【2】已知 f(x) 是定义在R上的奇函数,当x>0时, f(x)=x2+x-1, 求函数f(x)的表达式.引申:如果改为偶函数呢?一、奇函数、偶函数的图象性质1.奇函数的图象关于原点成中心对称图形;2.偶函数的图象关于y 轴成轴对称图形.奇偶函数图象的性质可用于:
①简化函数图象的画法;
②判断函数的奇偶性.例题讲解 例1. 已知函数y=f(x)是偶函数,它在y轴右边的图象如图,画出y=f(x)在 y轴左边的图象.解:画法略(一)简化函数图象的画法【1】作出函数 y=x2 -2|x|-3 的图象.-31-1练一练点评:用对称法作图时,先作出 x≥0的图象,由函数是偶函数,再用对称法作出另一半的图象.【2】如果奇函数f(x)在区间[3,7]上为增函数,且最小值是5,则在区间[-7,-3]上有没有最大值?是多少?解:如图所示函数有最大值 函数f(x)在区间[-7,-3]上为增函数.【3】已知f(x)是偶函数,g(x)是奇函数,
试将下图补充完整。【4】判断下列函数的奇偶性:
(非奇非偶函数)(奇函数)0............(偶函数)【5】已知f(x)=x5+bx3+cx且f(-2)=10,那么f(2)等于( )。
A、-10 B、10 C、20 D、与b、c有关
【6】下面四个命题中,正确的个数是( )
①奇函数的图像关于原点对称。
②偶函数的图像关于y轴对称。
③奇函数的图像一定过原点。
④偶函数的图像一定与y轴相交。
A、4 B、3 C、2 D、1
【7】如果定义在[3-a,5]上的函数f(x)为奇函数,那么,
a= ________ AC82-2思考你能画出f(x)的大致图像吗 ?答案:课堂小结1.函数奇偶性的定义. 定义法利用性质2.函数奇偶性的判定图象法:画出函数图象①考查函数定义域是否关于原点对称;
②判断f(-x)=±f(x)之一是否成立;
③作出结论.一个函数为奇函数?它的图象关于原点对称.一个函数为偶函数?它的图象关于y 轴对称.3.性质: 奇函数在关于原点对称的区间上具有相同的单调性;偶函数在关于原点对称的区间上具有相反的单调性.(2)在定义域的关于原点对称的公共区间内奇±奇=奇;偶±偶=偶;奇±偶=非奇非偶.偶×偶=偶;奇×奇=偶;偶×奇=奇.(1)奇函数、偶函数的图象特点(3)奇偶性与单调性的关系
