福建省晋江市季延中学人教版高中数学选修1-1课件:3.3.2函数的极值与导数 (共17张PPT)
文档属性
| 名称 | 福建省晋江市季延中学人教版高中数学选修1-1课件:3.3.2函数的极值与导数 (共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 183.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-18 09:16:41 | ||
图片预览



文档简介
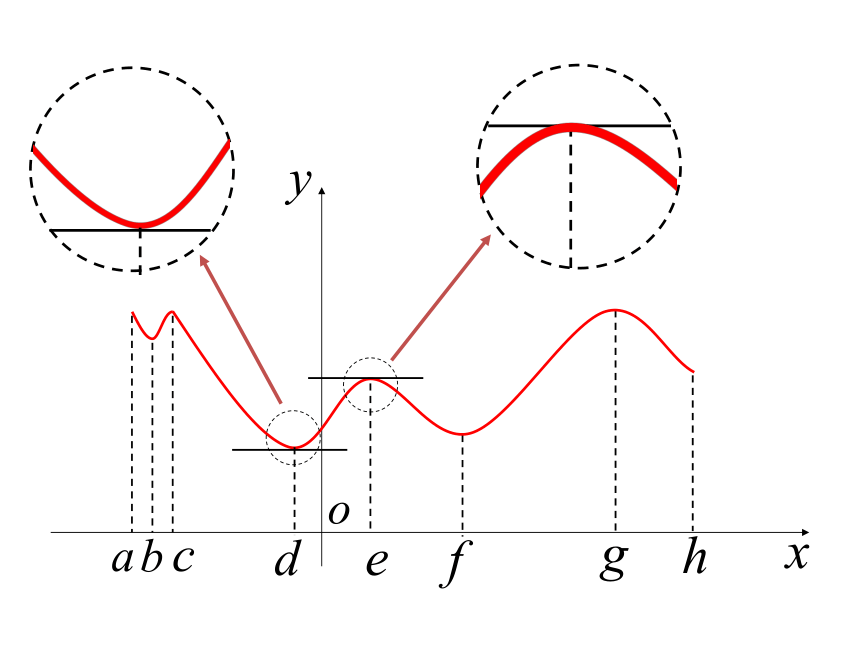
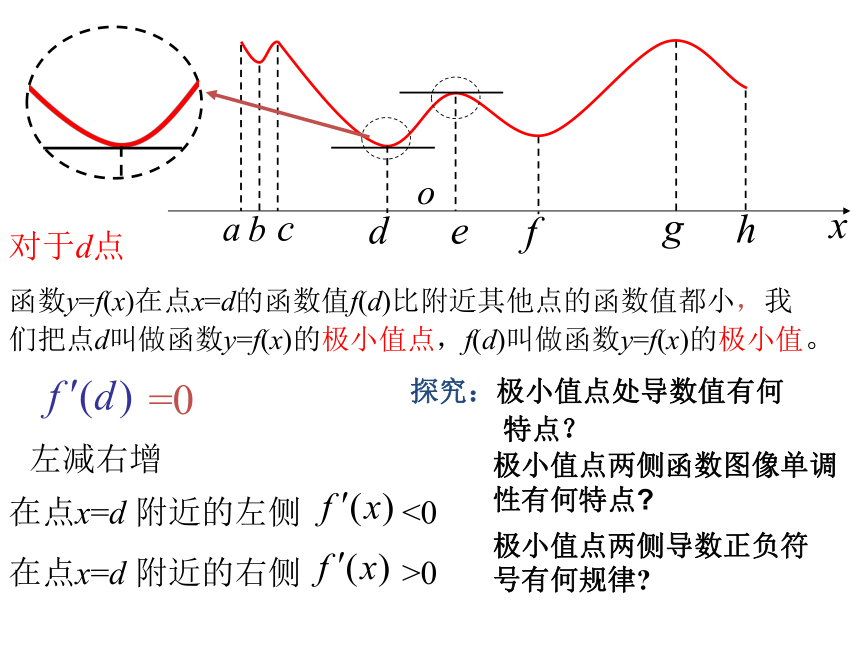
课件17张PPT。3.3.2函数的极值与导数第三章 导数及其应用对于d点
函数y=f(x)在点x=d的函数值f(d)比附近其他点的函数值都小,我们把点d叫做函数y=f(x)的极小值点,f(d)叫做函数y=f(x)的极小值。在点x=d 附近的左侧 <0
在点x=d 附近的右侧 >0 =0 极小值点两侧函数图像单调性有何特点?极小值点两侧导数正负符号有何规律?探究:极小值点处导数值有何
特点?左减右增在点 x=e 附近的左侧 >0
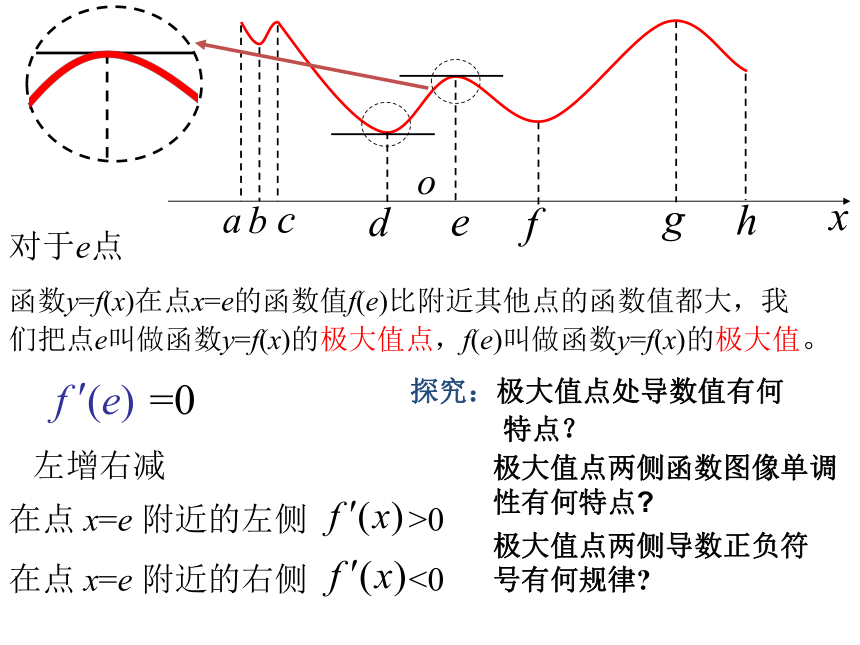
在点 x=e 附近的右侧 <0对于e点
函数y=f(x)在点x=e的函数值f(e)比附近其他点的函数值都大,我们把点e叫做函数y=f(x)的极大值点,f(e)叫做函数y=f(x)的极大值。
=0 探究:极大值点处导数值有何
特点?极大值点两侧函数图像单调性有何特点?极大值点两侧导数正负符号有何规律?左增右减极小值点、极大值点统称为极值点(横坐标)极小值、极大值统称为极值(纵坐标)理解极值概念时需注意的几点
(1)函数的极值是一个局部性的概念,是仅对某一点的左右两侧附近的点而言的.
(2)极值点是函数定义域内的点,而函数定义域的端点绝不是函数的极值点.
(3)若f(x)在[a,b]内有极值,那么f(x)在[a,b]内绝不是单调函数,即在定义域区间上的单调函数没有极值. (4)极大值与极小值没有必然的大小关系.一个函数在其定义域内可以有许多个极小值和极大值,在某一点的极小值可能大于另一点的极大值.(如图(1))(5)若函数f(x)在[a,b]上有极值,它的极值点的分布是有规律的(如图(2)所示),相邻两个极大值点之间必有一个极小值点,同样相邻两个极小值点之间必有一个极大值点.因为 所以例1 求函数 的极值.解:令 解得 或当 , 即 , 或 ;
当 , 即 .当 x 变化时, f (x) 的变化情况如下表:– ++单调递增单调递减单调递增所以, 当 x = –2 时, f (x)有极大值 28 / 3 ;当 x = 2 时, f (x)有极小值 – 4 / 3 .求解函数极值的一般步骤:
(1)确定函数的定义域
(2)求方程f’(x)=0的根
(3)用方程f’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(4)由f’(x)在方程f’(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况变式求下列函数的极值:解: 令 解得 列表:+单调递增单调递减– 所以, 当 时, f (x)有极小值求下列函数的极值:解: 解得 列表:– ++单调递增单调递减单调递增所以, 当 x = –3 时, f (x)有极大值 54 ;当 x = 3 时, f (x)有极小值 – 54 .求下列函数的极值:解: 解得 所以, 当 x = –2 时, f (x)有极小值 – 10 ;当 x = 2 时, f (x)有极大值 22 .解得 所以, 当 x = –1 时, f (x)有极小值 – 2 ;当 x = 1 时, f (x)有极大值 2 .例2、已知函数f(x)=ax3+bx2-2x在x=-2,x=1
处取得极值:
(1)求函数的解析式;
(2)求函数f(x)的单调区间。解:(1) =3ax2+2bx-2因为f(x)在x=-2,x=1处取得极值,所以 即解得 =x2+x-2由 >0,得x<-2或x>1,
所以f(x)的单调增区间为(-∞,-2) ∪(1,+∞)由 <0,得-2所以f(x)的单调减区间为(-2,1)导数值为0的点一定是函数的极值点吗?思考但x=0不是函数的极值点导数为零的点是
该点为极值点的必要条件,
而不是充分条件.一般地,求函数的极值的方法是:
解方程 =0.当 =0时.
①如果在x0附近的左侧 右侧
那么,f(x0)是极大值;
②如果在x0附近的左侧 右侧
那么,f(x0)是极小值.即“峰顶”即“谷底”小结求解函数极值的一般步骤:
(1)确定函数的定义域
(2)求方程f’(x)=0的根
(3)用方程f’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(4)由f’(x)在方程f’(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
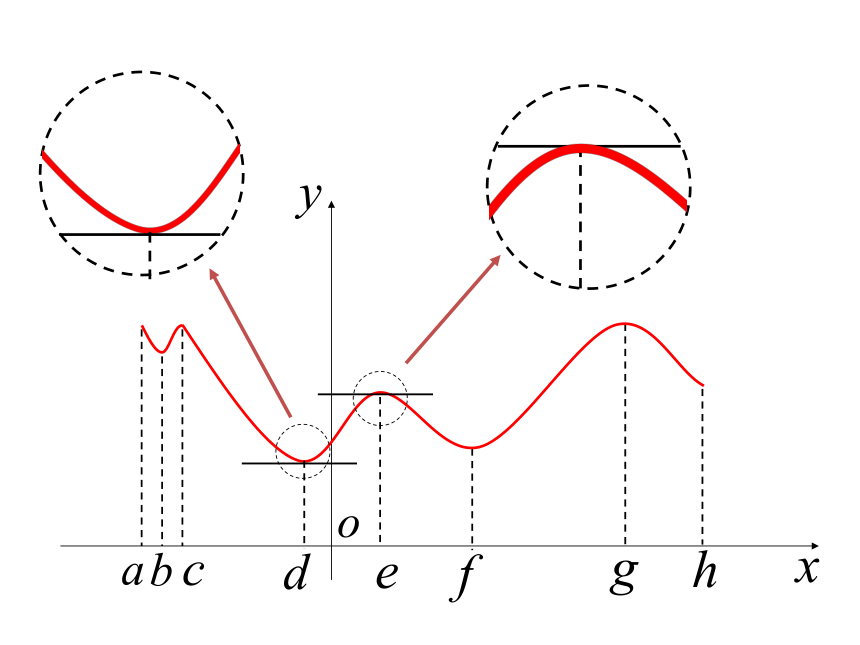
函数y=f(x)在点x=d的函数值f(d)比附近其他点的函数值都小,我们把点d叫做函数y=f(x)的极小值点,f(d)叫做函数y=f(x)的极小值。在点x=d 附近的左侧 <0
在点x=d 附近的右侧 >0 =0 极小值点两侧函数图像单调性有何特点?极小值点两侧导数正负符号有何规律?探究:极小值点处导数值有何
特点?左减右增在点 x=e 附近的左侧 >0
在点 x=e 附近的右侧 <0对于e点
函数y=f(x)在点x=e的函数值f(e)比附近其他点的函数值都大,我们把点e叫做函数y=f(x)的极大值点,f(e)叫做函数y=f(x)的极大值。
=0 探究:极大值点处导数值有何
特点?极大值点两侧函数图像单调性有何特点?极大值点两侧导数正负符号有何规律?左增右减极小值点、极大值点统称为极值点(横坐标)极小值、极大值统称为极值(纵坐标)理解极值概念时需注意的几点
(1)函数的极值是一个局部性的概念,是仅对某一点的左右两侧附近的点而言的.
(2)极值点是函数定义域内的点,而函数定义域的端点绝不是函数的极值点.
(3)若f(x)在[a,b]内有极值,那么f(x)在[a,b]内绝不是单调函数,即在定义域区间上的单调函数没有极值. (4)极大值与极小值没有必然的大小关系.一个函数在其定义域内可以有许多个极小值和极大值,在某一点的极小值可能大于另一点的极大值.(如图(1))(5)若函数f(x)在[a,b]上有极值,它的极值点的分布是有规律的(如图(2)所示),相邻两个极大值点之间必有一个极小值点,同样相邻两个极小值点之间必有一个极大值点.因为 所以例1 求函数 的极值.解:令 解得 或当 , 即 , 或 ;
当 , 即 .当 x 变化时, f (x) 的变化情况如下表:– ++单调递增单调递减单调递增所以, 当 x = –2 时, f (x)有极大值 28 / 3 ;当 x = 2 时, f (x)有极小值 – 4 / 3 .求解函数极值的一般步骤:
(1)确定函数的定义域
(2)求方程f’(x)=0的根
(3)用方程f’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(4)由f’(x)在方程f’(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况变式求下列函数的极值:解: 令 解得 列表:+单调递增单调递减– 所以, 当 时, f (x)有极小值求下列函数的极值:解: 解得 列表:– ++单调递增单调递减单调递增所以, 当 x = –3 时, f (x)有极大值 54 ;当 x = 3 时, f (x)有极小值 – 54 .求下列函数的极值:解: 解得 所以, 当 x = –2 时, f (x)有极小值 – 10 ;当 x = 2 时, f (x)有极大值 22 .解得 所以, 当 x = –1 时, f (x)有极小值 – 2 ;当 x = 1 时, f (x)有极大值 2 .例2、已知函数f(x)=ax3+bx2-2x在x=-2,x=1
处取得极值:
(1)求函数的解析式;
(2)求函数f(x)的单调区间。解:(1) =3ax2+2bx-2因为f(x)在x=-2,x=1处取得极值,所以 即解得 =x2+x-2由 >0,得x<-2或x>1,
所以f(x)的单调增区间为(-∞,-2) ∪(1,+∞)由 <0,得-2
该点为极值点的必要条件,
而不是充分条件.一般地,求函数的极值的方法是:
解方程 =0.当 =0时.
①如果在x0附近的左侧 右侧
那么,f(x0)是极大值;
②如果在x0附近的左侧 右侧
那么,f(x0)是极小值.即“峰顶”即“谷底”小结求解函数极值的一般步骤:
(1)确定函数的定义域
(2)求方程f’(x)=0的根
(3)用方程f’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(4)由f’(x)在方程f’(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
