六年级数学下册教案 运算律 2(北师大版)
文档属性
| 名称 | 六年级数学下册教案 运算律 2(北师大版) |

|
|
| 格式 | rar | ||
| 文件大小 | 16.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-29 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
运算律
教学内容:
六年级数学下册第58~59页。
教学目标:
1.理解并掌握加法运算律和乘法运算律,并能够用字母来表示。
2.能运用运算定律进行一些简便运算。
3.能根据具体情况,选择算法,发展思维的灵活性。
4.在数学活动中获得成功的体验,进一步增强对数学的兴趣和信心,进一步形成独立思考和探究问题的意识、习惯。
教学重点:
准确运用运算律进行简便计算。
教学难点:
选择合理灵活的方法进行简便计算。
教学过程:
一、创设情景,导入复习。
1. 小明是六年级的学生。上星期天爸爸妈妈都加班去了,小明想:我应该帮爸妈做点事,买菜去吧!顺便还练练数学的口算呢。进入菜场,他问了龙虾的单价是每千克2.5元,就称了1.4千克,可当他在脑中刚摆2.5×1.4的竖式时,卖龙虾的就口算报出:“应付3.5元钱”。
你知道卖龙虾的是怎样算的吗?
2. 小明请教了算法后,又去一个卖蔬菜的哪儿买了3.85元的大蒜和5.65元的冬瓜,算的也真快。可当他付出20元钱,正在脑中列出算式20-3.85-5.65准备依次从左往右口算时, 卖蔬菜的却已找回了11元钱。你知道卖蔬菜的是怎样算的吗?
3. 卖龙虾的和卖蔬菜的实际上就是应用了我们以前所学的什么知识来口算的呢?(板书课题:运算定律、性质)
4. 我们学习过哪几个运算定律和性质?(在学生回忆互说时板书:加法交换律、加法结合律、乘法交换律、乘法结合律、乘法分配律、减法的性质、除法的性质)
二、回顾整理、构建网络。
1. 请同学们回忆一下、然后同桌相互说说这几个运算定律和性质的具体意思是什么。
2. 小组合作填表。
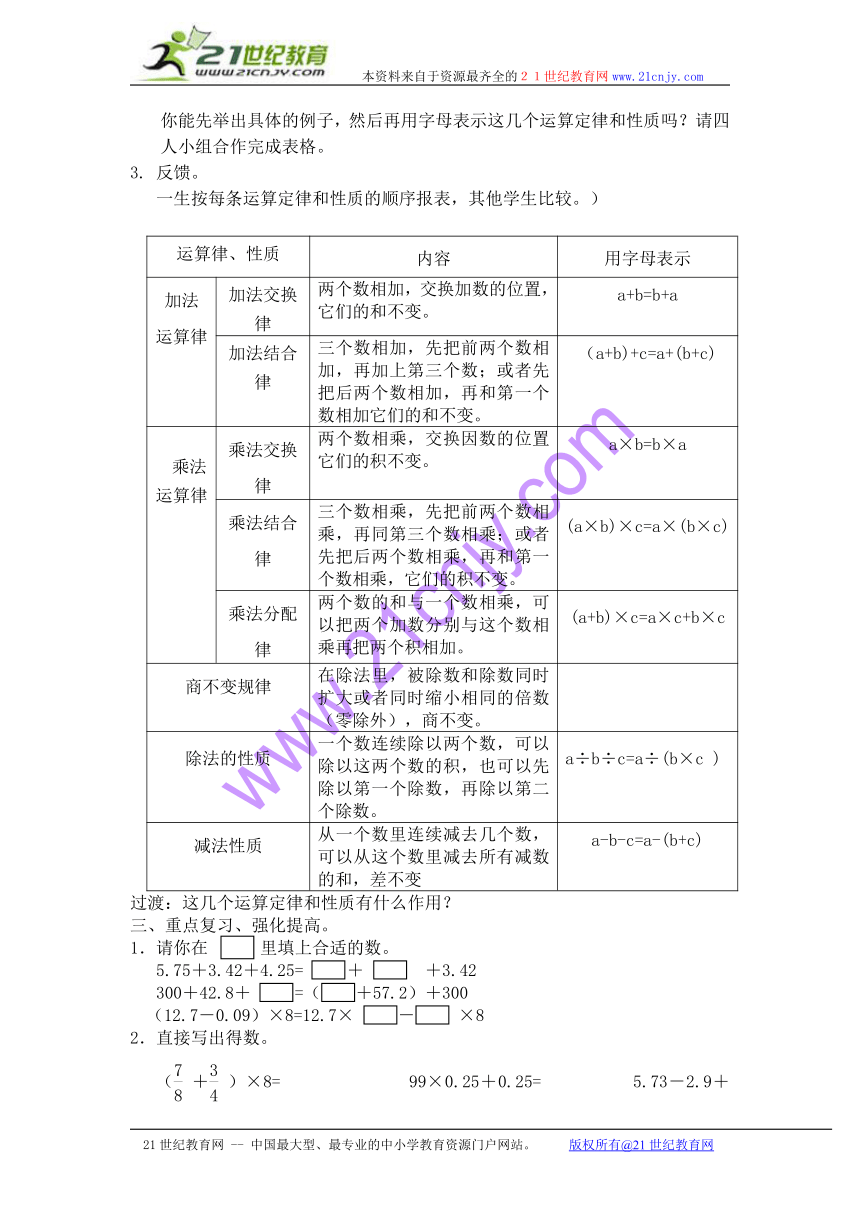
你能先举出具体的例子,然后再用字母表示这几个运算定律和性质吗?请四人小组合作完成表格。
3. 反馈。
一生按每条运算定律和性质的顺序报表,其他学生比较。)
运算律、性质 内容 用字母表示
加法运算律 加法交换律 两个数相加,交换加数的位置,它们的和不变。 a+b=b+a
加法结合律 三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再和第一个数相加它们的和不变。 (a+b)+c=a+(b+c)
乘法运算律 乘法交换律 两个数相乘,交换因数的位置它们的积不变。 a×b=b×a
乘法结合律 三个数相乘,先把前两个数相乘,再同第三个数相乘;或者先把后两个数相乘,再和第一个数相乘,它们的积不变。 (a×b)×c=a×(b×c)
乘法分配律 两个数的和与一个数相乘,可以把两个加数分别与这个数相乘再把两个积相加。 (a+b)×c=a×c+b×c
商不变规律 在除法里,被除数和除数同时扩大或者同时缩小相同的倍数(零除外),商不变。
除法的性质 一个数连续除以两个数,可以除以这两个数的积,也可以先除以第一个除数,再除以第二个除数。 a÷b÷c=a÷(b×c )
减法性质 从一个数里连续减去几个数,可以从这个数里减去所有减数的和,差不变 a-b-c=a-(b+c)
过渡:这几个运算定律和性质有什么作用?
三、重点复习、强化提高。
1.请你在 里填上合适的数。
5.75+3.42+4.25= + +3.42
300+42.8+ =( +57.2)+300
(12.7-0.09)×8=12.7× - ×8
2.直接写出得数。
(+)×8= 99×0.25+0.25= 5.73-2.9+2.9=
7.2÷100+0.72÷10= × +×= 2--=
3. 课本第59页巩固与应用的第1题。(可选做几道)
鼓励学生在运算的过程中熟悉运算律的“结构”,同时培养简算的意识。
4. 课本第59页巩固与应用的第2题。
先由学生独立做,然后交流,通过不同解题方法的比较,让学生再次体会乘法分配律。
四、自主检评,完善提高
(一)自主检评。
1.选择。
(1)3.2×4.9+6.8×4.9的简便算法是( )。
A.4.9×(3.2+6.8) B.(3.2+6.8)×4.9×2 C.(3.2×6.8)×4.9
(2)25×4.4=25×4×1.1应用了( )。
A.乘法交换律 B.乘法结合律 C.乘法分配律
(3)(+)×30=×30+×30,这里运用了乘法( )。
A.交换律 B.结合律 C.分配律
2.用简便方法计算下面各题。
11-6-1 79×101 125×42×8 304×99+304
3.下面各题 的计算正确吗?把错误的地方改正过来。
1.5-+=5-(+)=4
2.8×+8×+8=8×(++8)
3.(25+2.5)×4=25×4+2.5×4
4.25×××=(25×)+(×)=10+=10
(二)交流、评价。
四、归纳小结、课外延伸。
1. 通过本节课的复习,你有什么新的收获或感受?
﹡2. 课外延伸。
356-198= 2008×=
五、作业。
1.用简便方法计算下面各题。
12.5×2.4 2.75×29-1.75×29 8.48—2.61-1.39
÷+÷ (21+)÷ 6--
2.面粉每千克2.6元,大米每千克3.2元。买面粉和大米各50千克,共需要多少元?
3.学校运来180本中演草,120本中笔记,把这些本子平均分给5个班,每班分到多
少本?
板书设计:
运算律、性质
运算律、性质 内容 用字母表示
加法运算律 加法交换律 两个数相加,交换加数的位置,它们的和不变。 a+b=b+a
加法结合律 三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再和第一个数相加它们的和不变。 (a+b)+c=a+(b+c)
乘法运算律 乘法交换律 两个数相乘,交换因数的位置它们的积不变。 a×b=b×a
乘法结合律 三个数相乘,先把前两个数相乘,再同第三个数相乘;或者先把后两个数相乘,再和第一个数相乘,它们的积不变。 (a×b)×c=a×(b×c)
乘法分配律 :两个数的和与一个数相乘,可以把两个加数分别与这个数相乘再把两个积相加。 (a+b)×c=a×c+b×c
商不变规律 在除法里,被除数和除数同时扩大或者同时缩小相同的倍数(零除外),商不变。
除法的性质 一个数连续除以两个数,可以除以这两个数的积,也可以先除以第一个除数,再除以第二个除数。 a÷b÷c=a÷(b×c )
减法性质 从一个数里连续减去几个数,可以从这个数里减去所有减数的和,差不变 a-b-c=a-(b+c)
教后记:
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
运算律
教学内容:
六年级数学下册第58~59页。
教学目标:
1.理解并掌握加法运算律和乘法运算律,并能够用字母来表示。
2.能运用运算定律进行一些简便运算。
3.能根据具体情况,选择算法,发展思维的灵活性。
4.在数学活动中获得成功的体验,进一步增强对数学的兴趣和信心,进一步形成独立思考和探究问题的意识、习惯。
教学重点:
准确运用运算律进行简便计算。
教学难点:
选择合理灵活的方法进行简便计算。
教学过程:
一、创设情景,导入复习。
1. 小明是六年级的学生。上星期天爸爸妈妈都加班去了,小明想:我应该帮爸妈做点事,买菜去吧!顺便还练练数学的口算呢。进入菜场,他问了龙虾的单价是每千克2.5元,就称了1.4千克,可当他在脑中刚摆2.5×1.4的竖式时,卖龙虾的就口算报出:“应付3.5元钱”。
你知道卖龙虾的是怎样算的吗?
2. 小明请教了算法后,又去一个卖蔬菜的哪儿买了3.85元的大蒜和5.65元的冬瓜,算的也真快。可当他付出20元钱,正在脑中列出算式20-3.85-5.65准备依次从左往右口算时, 卖蔬菜的却已找回了11元钱。你知道卖蔬菜的是怎样算的吗?
3. 卖龙虾的和卖蔬菜的实际上就是应用了我们以前所学的什么知识来口算的呢?(板书课题:运算定律、性质)
4. 我们学习过哪几个运算定律和性质?(在学生回忆互说时板书:加法交换律、加法结合律、乘法交换律、乘法结合律、乘法分配律、减法的性质、除法的性质)
二、回顾整理、构建网络。
1. 请同学们回忆一下、然后同桌相互说说这几个运算定律和性质的具体意思是什么。
2. 小组合作填表。
你能先举出具体的例子,然后再用字母表示这几个运算定律和性质吗?请四人小组合作完成表格。
3. 反馈。
一生按每条运算定律和性质的顺序报表,其他学生比较。)
运算律、性质 内容 用字母表示
加法运算律 加法交换律 两个数相加,交换加数的位置,它们的和不变。 a+b=b+a
加法结合律 三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再和第一个数相加它们的和不变。 (a+b)+c=a+(b+c)
乘法运算律 乘法交换律 两个数相乘,交换因数的位置它们的积不变。 a×b=b×a
乘法结合律 三个数相乘,先把前两个数相乘,再同第三个数相乘;或者先把后两个数相乘,再和第一个数相乘,它们的积不变。 (a×b)×c=a×(b×c)
乘法分配律 两个数的和与一个数相乘,可以把两个加数分别与这个数相乘再把两个积相加。 (a+b)×c=a×c+b×c
商不变规律 在除法里,被除数和除数同时扩大或者同时缩小相同的倍数(零除外),商不变。
除法的性质 一个数连续除以两个数,可以除以这两个数的积,也可以先除以第一个除数,再除以第二个除数。 a÷b÷c=a÷(b×c )
减法性质 从一个数里连续减去几个数,可以从这个数里减去所有减数的和,差不变 a-b-c=a-(b+c)
过渡:这几个运算定律和性质有什么作用?
三、重点复习、强化提高。
1.请你在 里填上合适的数。
5.75+3.42+4.25= + +3.42
300+42.8+ =( +57.2)+300
(12.7-0.09)×8=12.7× - ×8
2.直接写出得数。
(+)×8= 99×0.25+0.25= 5.73-2.9+2.9=
7.2÷100+0.72÷10= × +×= 2--=
3. 课本第59页巩固与应用的第1题。(可选做几道)
鼓励学生在运算的过程中熟悉运算律的“结构”,同时培养简算的意识。
4. 课本第59页巩固与应用的第2题。
先由学生独立做,然后交流,通过不同解题方法的比较,让学生再次体会乘法分配律。
四、自主检评,完善提高
(一)自主检评。
1.选择。
(1)3.2×4.9+6.8×4.9的简便算法是( )。
A.4.9×(3.2+6.8) B.(3.2+6.8)×4.9×2 C.(3.2×6.8)×4.9
(2)25×4.4=25×4×1.1应用了( )。
A.乘法交换律 B.乘法结合律 C.乘法分配律
(3)(+)×30=×30+×30,这里运用了乘法( )。
A.交换律 B.结合律 C.分配律
2.用简便方法计算下面各题。
11-6-1 79×101 125×42×8 304×99+304
3.下面各题 的计算正确吗?把错误的地方改正过来。
1.5-+=5-(+)=4
2.8×+8×+8=8×(++8)
3.(25+2.5)×4=25×4+2.5×4
4.25×××=(25×)+(×)=10+=10
(二)交流、评价。
四、归纳小结、课外延伸。
1. 通过本节课的复习,你有什么新的收获或感受?
﹡2. 课外延伸。
356-198= 2008×=
五、作业。
1.用简便方法计算下面各题。
12.5×2.4 2.75×29-1.75×29 8.48—2.61-1.39
÷+÷ (21+)÷ 6--
2.面粉每千克2.6元,大米每千克3.2元。买面粉和大米各50千克,共需要多少元?
3.学校运来180本中演草,120本中笔记,把这些本子平均分给5个班,每班分到多
少本?
板书设计:
运算律、性质
运算律、性质 内容 用字母表示
加法运算律 加法交换律 两个数相加,交换加数的位置,它们的和不变。 a+b=b+a
加法结合律 三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再和第一个数相加它们的和不变。 (a+b)+c=a+(b+c)
乘法运算律 乘法交换律 两个数相乘,交换因数的位置它们的积不变。 a×b=b×a
乘法结合律 三个数相乘,先把前两个数相乘,再同第三个数相乘;或者先把后两个数相乘,再和第一个数相乘,它们的积不变。 (a×b)×c=a×(b×c)
乘法分配律 :两个数的和与一个数相乘,可以把两个加数分别与这个数相乘再把两个积相加。 (a+b)×c=a×c+b×c
商不变规律 在除法里,被除数和除数同时扩大或者同时缩小相同的倍数(零除外),商不变。
除法的性质 一个数连续除以两个数,可以除以这两个数的积,也可以先除以第一个除数,再除以第二个除数。 a÷b÷c=a÷(b×c )
减法性质 从一个数里连续减去几个数,可以从这个数里减去所有减数的和,差不变 a-b-c=a-(b+c)
教后记:
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
