22.3相似三角形的性质 课件
图片预览




文档简介
(共37张PPT)
22.3 相似三角形的性质
(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
(2)如何判定两个三角形相似?
①定义;
②预备定理(平行);
③三边对应成比例;
④两个角对应相等;
⑤两边对应成比例,且夹角相等;
温故知新
直角三角形(HL)
A
B
C
A/
B/
C/
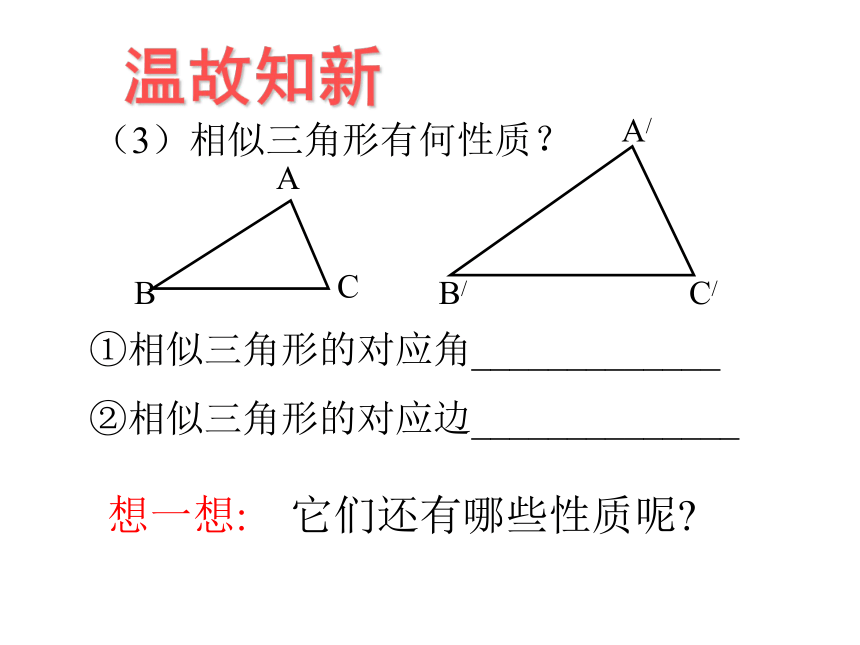
①相似三角形的对应角_____________
②相似三角形的对应边______________
想一想: 它们还有哪些性质呢
温故知新
(3)相似三角形有何性质?
(1)一个三角形有三条重要线段:
________________
(2)如果两个三角形相似,那么这些对应线段有什么关系呢?
你知我知?
高、中线、角平分线
A
C
B
A′
B′
C′
∽
(1)
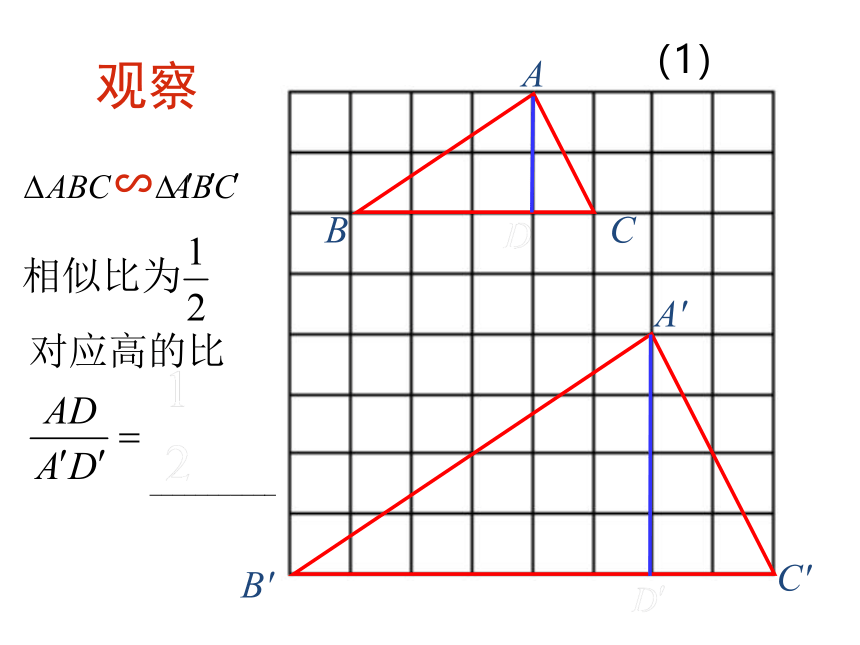
观察
A
C
B
A′
B′
C′
∽
(2)
A
C
B
A′
B′
C′
∽
(3)
∽
可得:
小结
观察这些数据,你会有怎样的猜想呢?
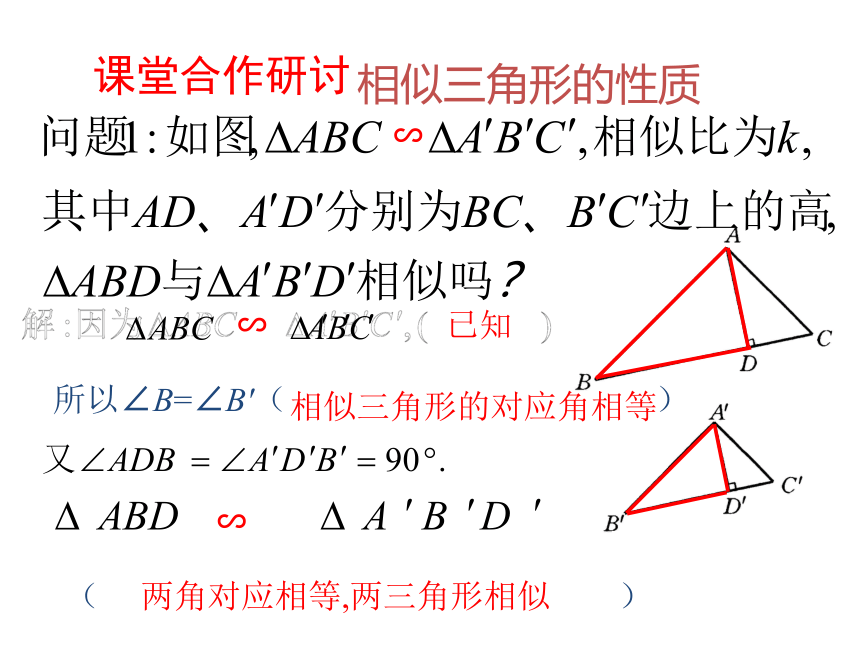
课堂合作研讨
两角对应相等,两三角形相似
∽
∽
已知
所以∠B=∠B′( )
相似三角形的对应角相等
∽
( )
相似三角形的性质
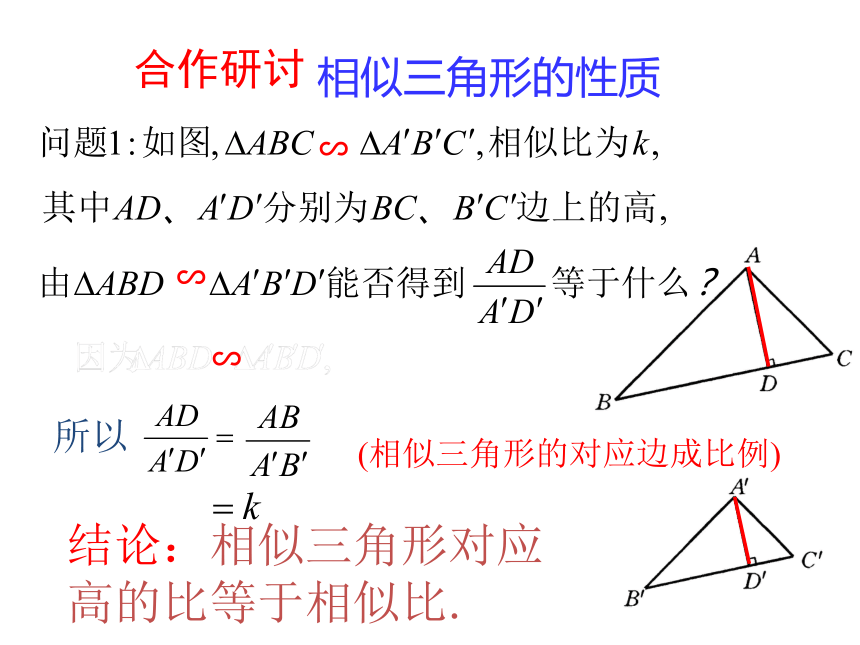
合作研讨
∽
所以
(相似三角形的对应边成比例)
∽
∽
相似三角形的性质
结论:相似三角形对应高的比等于相似比.
类似结论
D'
C'
B'
A'
D
C
B
A
∽
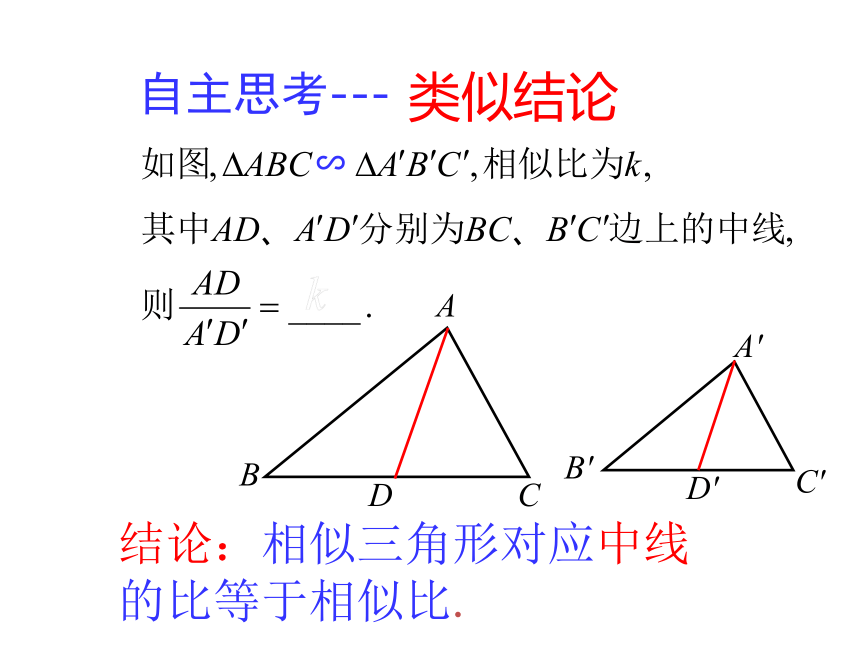
自主思考---
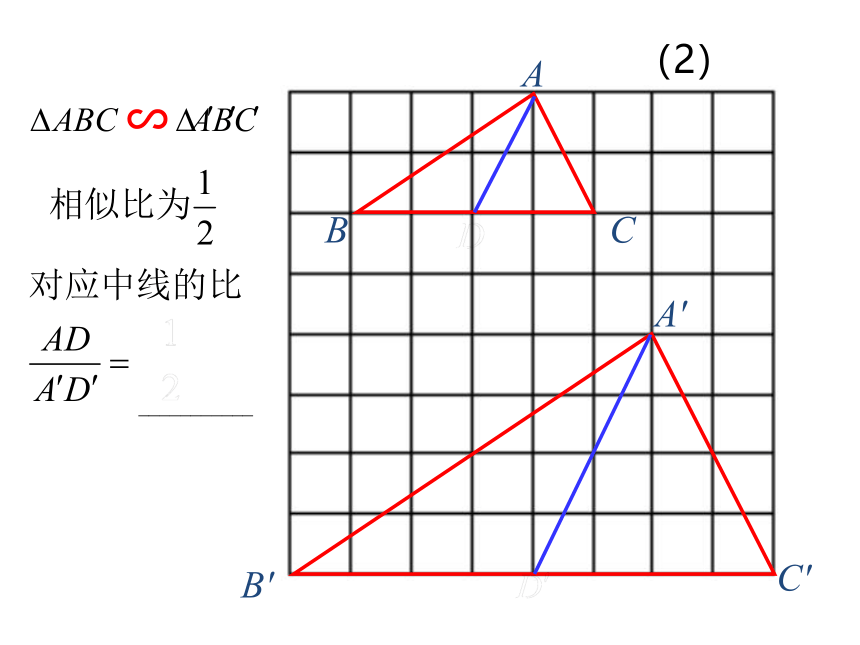
结论:相似三角形对应中线的比等于相似比.
A′
C′
B′
C
B
A
E′
E
∽
类似结论
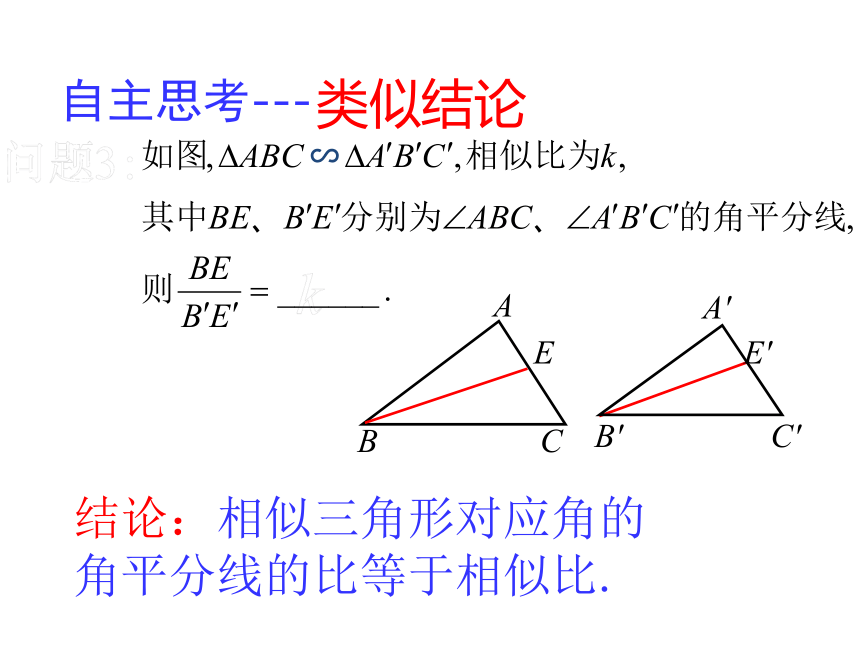
自主思考---
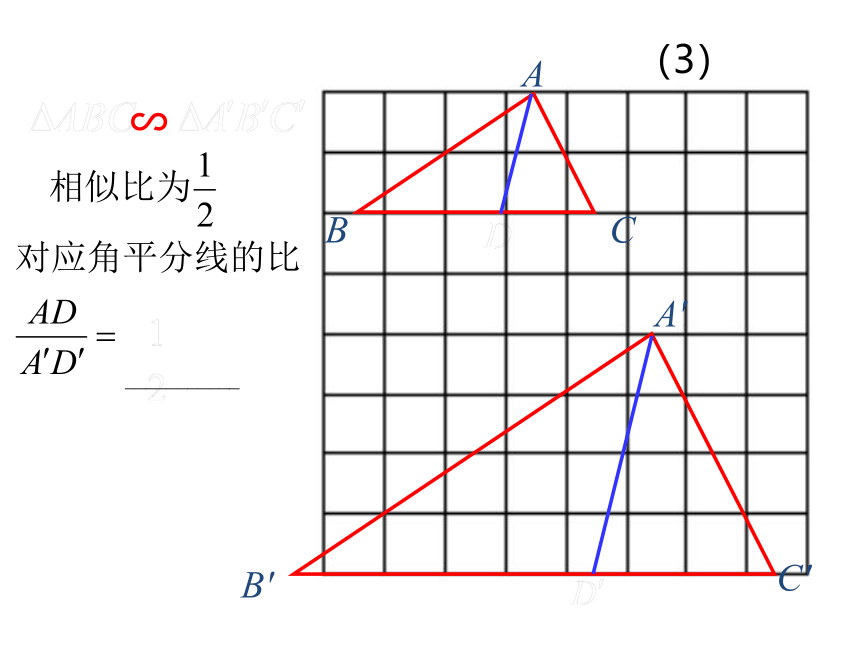
结论:相似三角形对应角的角平分线的比等于相似比.
对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形
都等于相似比.
相似三角形的性质
填一填
1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.
2∶ 3
2 ∶ 3
2.两个相似三角形的相似比为1:4, 则对应高的比为_________,对应角的角平分线的比为_________.
1:4
1:4
3.两个相似三角形对应中线的比为 ,
则相似比为______,对应高的比为______ .
图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?
(1)
(2)
(3)
1
2
3
观察与思考
(1)与(2)的相似比=______,
(1)与(2)的周长比=______
(2)与(3)的相似比=______,
(2)与(3)的周长比=______
1∶ 2
结论:相似三角形的周长比等于______.
相似比
(都相似)
2∶ 3
1∶ 2
2∶ 3
两个相似三角形的周长比会等于相似比吗?
问题探究:
已知△ABC∽△ ,且相似比为k。
求证:△ABC、 周长的比等于k
证明:
△ABC∽△
即△ABC、△ 的周长比等于相似比
∵
∴
∴
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
都等于相似比.
相似三角形的性质
两个相似三角形的面积之间有什么关系呢?
问题探究:
观察与思考
1
2
3
1∶ 2
当相似比=k时,面积比=k2.
(1)
(2)
(3)
(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______
1∶ 4
2∶ 3
4∶ 9
相似三角形面积的比等于相似比的平方.
已知△ABC∽△ ,且相似比为k,AD、 分别是△ABC、△ 对应边BC、 上的高 ,求证:
证明:
∵△ABC∽△
∴
∴
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
都等于相似比.
面积的比等于相似比的平方
相似三角形的性质
例:已知△ABC∽ △A B C ,BD和B D 分别是△ABC和△A B C 中线,且AB=10,A B =2,BD=6。求B D 的长。
解:∵ △ABC∽△A B C
∴
=
=
B D =1.2
答:B D 的长为1.2。
AB
A B
BD
B D
10
2
6
B D
A
B
C
D
A
B
C
D
(1)△ADE与△ABC相似吗?如果相似, 求它们的相似比.
A
B
C
D
E
1∶4
(2) △ADE的周长︰△ABC的周长=_______.
1∶4
例.如图,DE∥BC, DE = 1, BC = 4,
(4)
1.如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于______.
2.相似三角形对应边的比为2:5,
那么相似比为_______,
对应角的角平分线的比为______,
周长的比为_________,
面积的比为_________.
3∶5
2:5
课堂演练
2:5
2:5
4:25
3.把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的______倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的______倍。
(3)两个相似三角形的一对对应边分别是35厘米和14 厘米,①它们的周长差60厘米,这两个三角形的周长分别是______ ____。②它们的面积之和是58平方厘米,这两个三角形的面积分别是______________。
25
10
100cm、40cm
50cm2、8cm2
4:已知△ABC∽△DEF,BG、EH分别是△ABC和 △DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长。
解:∵ △ABC∽△DEF
∴ BC∶EF=BG∶EH
6∶4=4.8∶EH
EH=3.2(cm)
答:EH的长为3.2cm。
A
G
B
C
D
E
F
H
课堂训练
1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结
相似比的平方
相似三角形的性质
相似多边形也有同样的结论
比例
相等
相似比
相似比
1.如果两个三角形相似,相似比为3∶5,那么对应角的角平分线的比等于多少?
2.相似三角形对应边的比为0.4,那么相似比为______,对应角的角平分线的比为______,周长的比为______,面积的比为______.
3∶5
0.4
0.4
0.16
3、若两个三角形面积之比为16:9,则它们的对高之比为_____,对应中线之比为_____
4 : 3
4 : 3
0.4
课堂检测
4.如图,在 ABCD中,若E是AB的中点,
则(1) AEF与 CDF的相似比为______.
(2)若 AEF的面积为5cm2,
则 CDF的面积为______.
B
F
E
D
C
A
1 : 2
20 cm2
∵ AEF与 CDF
拓展训练
1、平行四边形ABCD与平行四边形 相似,
已知AB=5,对应边 =6,平行四边形
ABCD的面积为10,求平行四边形
的面积.
2、已知两个等边三角形的边长之比为2 :3,且它们的面积之和26cm2,则较小的等边三角形的面积为多少?
拓展训练
2:如图,△ABC~△A'B'C',它们的周长分别是60厘米和72厘米,且AB=15厘米,B'C'=24厘米。求:BC、AC、A'B'、A'C'。
C'
B'
A'
C
B
A
解:因为△ABC~△A'B'C' △ABC~△A'B'C
所以
?
?
?
=
=
?
AB
BC
A'B'
B'C'
60
72
又 AB=15厘米 B'C'=24厘米
所以 A'B'=18厘米 BC=20厘米
故 AC=60–15–20=25(厘米)A'C'=72–18–24=30(厘米)
3、如图,FG//BC,AE⊥FG,
AD⊥BC,E、D是垂足,FG=6,
BC=15,则(1)AE:AD是多少?
提高拓展
(3)若FGHI是正方形,它的边长是多少?你会把这个正方形剪出来吗?
变式训练
4、如图,FG//BC,AE⊥FG,
AD⊥BC,E、D是垂足,FG=6,
BC=15,则(1)AE:AD是多少?
(2)若AD=10,求ED的长
变式练习:
1、如图是一个照相机成像的示意图。如果底片AB宽35mm,焦距是70mm,拍摄5m外的景物A′B ′有多宽?如果焦距是50mm呢?
70mm
5m
A
B
A′
O
B′
大胆尝试
5.如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗 如果相似,求出△A1B1C1和△A2B2C2的面积比.
2 : 1
解:相似.
因为相似比是
所以面积比是
4 : 1
22.3 相似三角形的性质
(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
(2)如何判定两个三角形相似?
①定义;
②预备定理(平行);
③三边对应成比例;
④两个角对应相等;
⑤两边对应成比例,且夹角相等;
温故知新
直角三角形(HL)
A
B
C
A/
B/
C/
①相似三角形的对应角_____________
②相似三角形的对应边______________
想一想: 它们还有哪些性质呢
温故知新
(3)相似三角形有何性质?
(1)一个三角形有三条重要线段:
________________
(2)如果两个三角形相似,那么这些对应线段有什么关系呢?
你知我知?
高、中线、角平分线
A
C
B
A′
B′
C′
∽
(1)
观察
A
C
B
A′
B′
C′
∽
(2)
A
C
B
A′
B′
C′
∽
(3)
∽
可得:
小结
观察这些数据,你会有怎样的猜想呢?
课堂合作研讨
两角对应相等,两三角形相似
∽
∽
已知
所以∠B=∠B′( )
相似三角形的对应角相等
∽
( )
相似三角形的性质
合作研讨
∽
所以
(相似三角形的对应边成比例)
∽
∽
相似三角形的性质
结论:相似三角形对应高的比等于相似比.
类似结论
D'
C'
B'
A'
D
C
B
A
∽
自主思考---
结论:相似三角形对应中线的比等于相似比.
A′
C′
B′
C
B
A
E′
E
∽
类似结论
自主思考---
结论:相似三角形对应角的角平分线的比等于相似比.
对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形
都等于相似比.
相似三角形的性质
填一填
1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.
2∶ 3
2 ∶ 3
2.两个相似三角形的相似比为1:4, 则对应高的比为_________,对应角的角平分线的比为_________.
1:4
1:4
3.两个相似三角形对应中线的比为 ,
则相似比为______,对应高的比为______ .
图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?
(1)
(2)
(3)
1
2
3
观察与思考
(1)与(2)的相似比=______,
(1)与(2)的周长比=______
(2)与(3)的相似比=______,
(2)与(3)的周长比=______
1∶ 2
结论:相似三角形的周长比等于______.
相似比
(都相似)
2∶ 3
1∶ 2
2∶ 3
两个相似三角形的周长比会等于相似比吗?
问题探究:
已知△ABC∽△ ,且相似比为k。
求证:△ABC、 周长的比等于k
证明:
△ABC∽△
即△ABC、△ 的周长比等于相似比
∵
∴
∴
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
都等于相似比.
相似三角形的性质
两个相似三角形的面积之间有什么关系呢?
问题探究:
观察与思考
1
2
3
1∶ 2
当相似比=k时,面积比=k2.
(1)
(2)
(3)
(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______
1∶ 4
2∶ 3
4∶ 9
相似三角形面积的比等于相似比的平方.
已知△ABC∽△ ,且相似比为k,AD、 分别是△ABC、△ 对应边BC、 上的高 ,求证:
证明:
∵△ABC∽△
∴
∴
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
都等于相似比.
面积的比等于相似比的平方
相似三角形的性质
例:已知△ABC∽ △A B C ,BD和B D 分别是△ABC和△A B C 中线,且AB=10,A B =2,BD=6。求B D 的长。
解:∵ △ABC∽△A B C
∴
=
=
B D =1.2
答:B D 的长为1.2。
AB
A B
BD
B D
10
2
6
B D
A
B
C
D
A
B
C
D
(1)△ADE与△ABC相似吗?如果相似, 求它们的相似比.
A
B
C
D
E
1∶4
(2) △ADE的周长︰△ABC的周长=_______.
1∶4
例.如图,DE∥BC, DE = 1, BC = 4,
(4)
1.如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于______.
2.相似三角形对应边的比为2:5,
那么相似比为_______,
对应角的角平分线的比为______,
周长的比为_________,
面积的比为_________.
3∶5
2:5
课堂演练
2:5
2:5
4:25
3.把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的______倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的______倍。
(3)两个相似三角形的一对对应边分别是35厘米和14 厘米,①它们的周长差60厘米,这两个三角形的周长分别是______ ____。②它们的面积之和是58平方厘米,这两个三角形的面积分别是______________。
25
10
100cm、40cm
50cm2、8cm2
4:已知△ABC∽△DEF,BG、EH分别是△ABC和 △DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长。
解:∵ △ABC∽△DEF
∴ BC∶EF=BG∶EH
6∶4=4.8∶EH
EH=3.2(cm)
答:EH的长为3.2cm。
A
G
B
C
D
E
F
H
课堂训练
1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结
相似比的平方
相似三角形的性质
相似多边形也有同样的结论
比例
相等
相似比
相似比
1.如果两个三角形相似,相似比为3∶5,那么对应角的角平分线的比等于多少?
2.相似三角形对应边的比为0.4,那么相似比为______,对应角的角平分线的比为______,周长的比为______,面积的比为______.
3∶5
0.4
0.4
0.16
3、若两个三角形面积之比为16:9,则它们的对高之比为_____,对应中线之比为_____
4 : 3
4 : 3
0.4
课堂检测
4.如图,在 ABCD中,若E是AB的中点,
则(1) AEF与 CDF的相似比为______.
(2)若 AEF的面积为5cm2,
则 CDF的面积为______.
B
F
E
D
C
A
1 : 2
20 cm2
∵ AEF与 CDF
拓展训练
1、平行四边形ABCD与平行四边形 相似,
已知AB=5,对应边 =6,平行四边形
ABCD的面积为10,求平行四边形
的面积.
2、已知两个等边三角形的边长之比为2 :3,且它们的面积之和26cm2,则较小的等边三角形的面积为多少?
拓展训练
2:如图,△ABC~△A'B'C',它们的周长分别是60厘米和72厘米,且AB=15厘米,B'C'=24厘米。求:BC、AC、A'B'、A'C'。
C'
B'
A'
C
B
A
解:因为△ABC~△A'B'C' △ABC~△A'B'C
所以
?
?
?
=
=
?
AB
BC
A'B'
B'C'
60
72
又 AB=15厘米 B'C'=24厘米
所以 A'B'=18厘米 BC=20厘米
故 AC=60–15–20=25(厘米)A'C'=72–18–24=30(厘米)
3、如图,FG//BC,AE⊥FG,
AD⊥BC,E、D是垂足,FG=6,
BC=15,则(1)AE:AD是多少?
提高拓展
(3)若FGHI是正方形,它的边长是多少?你会把这个正方形剪出来吗?
变式训练
4、如图,FG//BC,AE⊥FG,
AD⊥BC,E、D是垂足,FG=6,
BC=15,则(1)AE:AD是多少?
(2)若AD=10,求ED的长
变式练习:
1、如图是一个照相机成像的示意图。如果底片AB宽35mm,焦距是70mm,拍摄5m外的景物A′B ′有多宽?如果焦距是50mm呢?
70mm
5m
A
B
A′
O
B′
大胆尝试
5.如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗 如果相似,求出△A1B1C1和△A2B2C2的面积比.
2 : 1
解:相似.
因为相似比是
所以面积比是
4 : 1
