【沪科版】数学七年级上册 课件 1.4有理数的加减(1) (共39张PPT)
文档属性
| 名称 | 【沪科版】数学七年级上册 课件 1.4有理数的加减(1) (共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 790.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-18 07:41:16 | ||
图片预览









文档简介
课件39张PPT。1.4有理数的加减(1) 在北京奥运会乒乓球男子团体决赛中,中国男队3比0击败德国男队,获得金牌,德国队获得银牌.首盘王皓3比0轻取奥恰洛夫;第二盘马琳出场,他以3比1力克波尔;第三盘双打比赛,王励勤/王皓3比1战胜苏斯/波尔.在这场比赛中,中国队三名队员的胜局怎么表示?德国队三名队员的胜局怎么表示?新课导入 中国乒乓球男团的三名队员在这场比赛中还可能出现其他的什么情况?你能列出算式吗? 知识与能力
1.经历探索有理数加法法则的过程,理解有理数加法的意义,理解并掌握有理数加法的法则;
2.应用有理数加法法则进行准确运算.教学目标过程与方法
1.通过有理数加法的学习,学习化归的意识、数形结合和分类的思想方法,培养观察、比较和概括的思维能力。
2.能够由特殊到一般,总结出有理数的加法法则,培养一定的归纳能力及语言表达能力。 教学目标情感态度与价值观
体会在总结有理数加法法则的过程中与他人合作、交流的重要性,并且意识到数学与现实生活是紧密相连的.教学目标重点
有理数加法法则.
难点
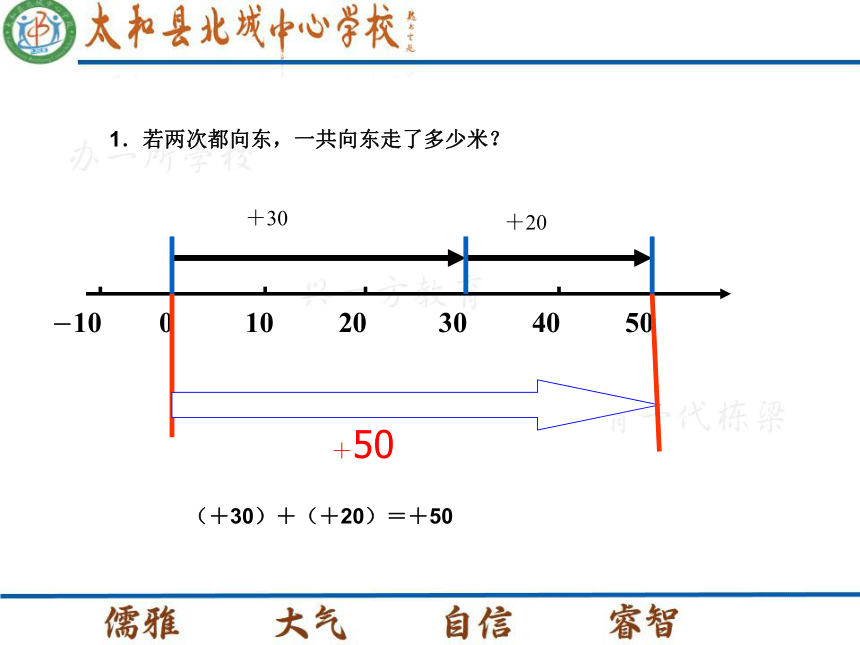
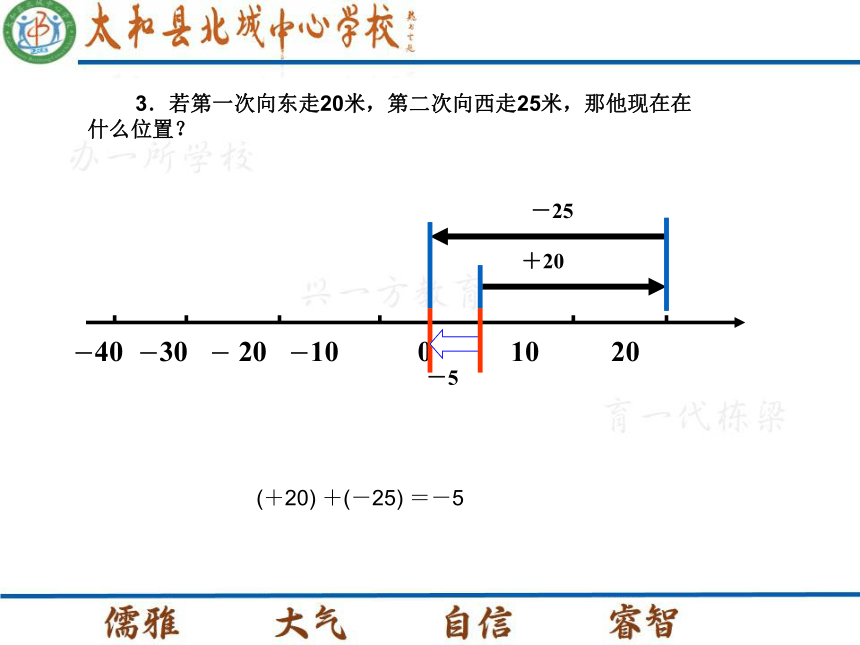
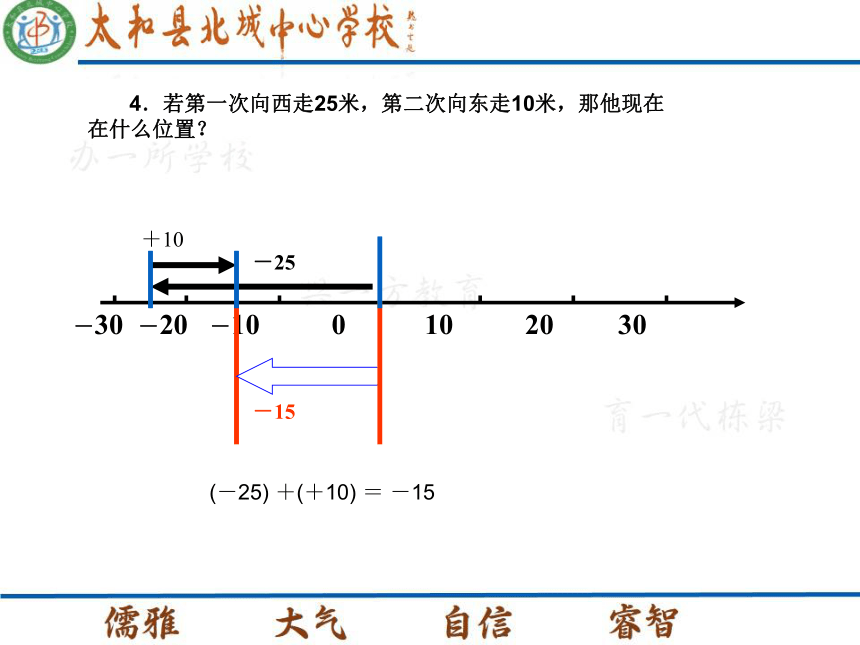
异号两数相加的法则. 教学重难点 小刚在一条东西向的跑道上,先走了30米,又走了20米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米? 1.若两次都向东,一共向东走了多少米? (+30)+(+20)=+50+30 +20+502.若两次都向西,一共向西走了多少米? (-30)+(-20)=-50-20 -30-50 3.若第一次向东走20米,第二次向西走25米,那他现在在什么位置? (+20) +(-25) =-5 -25 +20-5 4.若第一次向西走25米,第二次向东走10米,那他现在在什么位置? (-25) +(+10) = -15 -25 +10-15 5.若第一次向西走20米,第二次向东走20米,那他现在在什么位置? (-20) +(+20) =0+20 -20 6.若第一次向东走30米,第二次站在原地没动,那他现在在什么位置? (+30) +0=+30+30+30有理数加法有没有规律? 1.和的符号与两个加数的符号有什么关系?
2.和的绝对值与两个加数的绝对值又有什么关系?想一想 观察、比较下面几个式子,看能否从这些算式中得到启发,想办法归纳出有理数加法的法则? (+30)+(+20)=+50
(-30)+(-20)=-50
(?20)+(?25)=?5
(?25)+ (?10)= ?15
(?20)+(?20)=0
(+30)+0=+30有理数加法法则:
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.知识要点例1:计算:
(1)(-4)+(-8);
(2)(-5)+13;
(3)0+(-7);
(4)(-4.7)+3.9.解:(1)(-4)+(-8)
=-(4+8)
=-12
(2)(-5)+13=+(13-8)=8
(3)0+(-7)=-7
(4)(-4.7)+4.7=-4.7+4.7=0 互为相反意义的量可以全部抵消或部分抵消. 例2:足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.分析: 解:每个队的进球总数记为正数,失球总数记为负数,这两数的和为这队的净胜球数。
三场比赛中,红球共进4球,失2球,净胜球数为
(+4)+(-2)=+(4-2)=2
黄队共进2球,失4球,净胜球为
(+2)+(-4)=-(4-2)=-2
篮球共进( )球,失( )球,净胜球数为( ).11(+1)+(-1)=0(1)16+(-12)___(-12)+16;
(2)(-19)+(-8)____(-8)+(-19);
(3)(-6.9)+1.5 ___1.5+(-6.9);
(4)0.5+(-5.9)___(-5.9)+0.5. 在横线上填上适当的符号,使两边的式子成立.====加法的交换律
有理数的加法中,两个数的加法,交换加数的位置,和不变.
即:a+b=b+a 1.式子中的字母分别表示任意的一个有理数。(如:既可成表示整数,也可以表示分数;既可以表示正数,也可以表示负数或0).
2.在同一个式子中,同一个字母表示同一个数.知识要点(1)[16+(-12)] +2_____16+ [(-12)+2]
(2)[(-19)+(-8)] +6____(-19)+ [(-8)+6]
(3)[(-6.9)+1.5] +9____(-6.9) + [1.5+9]
(4)[0.5+(-5.9)] +(-8)_____0.5+ [(-5.9)+(-8)]==== 在横线上填上适当的符号,使两边的式子成立.加法的结合律
有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
即:(a+b)+c =a+(b+c).知识要点例3:计算:
(1)24+(-12)+20+(-15);
(2)(-2.54)+3.56+(-7.46)+(-3.56).解(1)24+(-12)+20+(-15)
=24+20+[(-12)+(-15)]
=44+(-27)
=17 这里使用了哪些运算律 ? (2)(-2.54)+3.56+(-7.46)+(-3.56)
=[(-2.54)+(-7.46)] +[(+3.56)+
(-3.56)]
=(-10)+0
=-10.有理的加法常用的三个规律: 1. 一般地,总是先把正数或负数分别结合在一起相加. 2.有相反数的可先把相反数相加,能凑整的可先凑整. 3.有分母相同的,可先把分母相同的数结合相加.归纳 例4:每袋小麦的标准重量为90千克,10袋小麦称重记录如图所示。与标准重量比较,10袋小麦总计超过多少千克或不足多少千克?10袋小麦的总重量是多少? 解法1:先计算10袋小麦的总重量
91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1+91.1=905.4
再计算总计超过多少千克:
905.4-90×10=5.4 解法2:每袋小麦超过标准重量的千克数记作正数,不足的千克数记作负数。
10袋小麦对应的数为+1,+1,+1.5,-1,+1.2,+1.3, -1.3,-1.2,+1.8,+1.1。
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)
+1.8+1.1
=[1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)]+
(1+1.5+1.8+1.1)
=5.4
90×10+5.4=905.4答:10袋不麦一共905.4千克,总计超过5.4千克. 数扩展到有理数之后,下面这些结论还成立吗?请说明理由.
(1)若两个数的和是0,则这两个数都是0;
(2)任何两数相加,和不小于任何一个加数.议一议1.加法法则: (1)同号两数相加,取相同的符号,并把绝对值相加;若a>0,b>0,则a+b=+(|a|+|b|);
若a<0,b<0,则a+b=- (|a|+|b|). 课堂小结 (2)绝对值不相等的异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值; 若a>0,b<0,且|a|>|b|,则a+b=+(|a|-|b|)
若a>0,b<0,且|a|>|b|,则a+b=- (|b|+|a|)(3)互为相反数的两个数相加得0;若a>0,b<0,且|a|=|b|,则a+b=0;a+0=a.(4)一个数同0相加,仍得这个数.2.加法运算律(1)加法交换律:
a+b=b+a;
(2)加法结合律:
(a+b)+c=a+(b+c). 1.如果两个有理数的和为正数,则下列正确的是( )
A.两个数一定都是正数
B.两数都不为零
C.两个数中至少有一个为正数
D.两个数中至少有一个为负数 C随堂练习2.计算解: 3.已知|a|=2,|b|=3,求a+b的值. 解:因为|a|=2,|b|=3,
所以a=±2,b=±3
所以当a=2,b=3时,a+b=2+3=5
当a=2,b=-3时,a+b=2+(-3)=-1
当a=-2,b=3时,a+b=-2+3=1
当a=-2,b=-3时,a+b=-2+(-3)=-5.解: 5.仓库内原存粮食3500千克,一周内存入和取出情况如下(存入为正,单位:千克):-1500,2000,-800,700,-1000,1200,-240,问第七天末仓库内还存有多少粮食?解:
3500-1500+2000-800+700-1000+1200-240 =3860
答:第七天末仓库内还存有3860千克粮食.
1.经历探索有理数加法法则的过程,理解有理数加法的意义,理解并掌握有理数加法的法则;
2.应用有理数加法法则进行准确运算.教学目标过程与方法
1.通过有理数加法的学习,学习化归的意识、数形结合和分类的思想方法,培养观察、比较和概括的思维能力。
2.能够由特殊到一般,总结出有理数的加法法则,培养一定的归纳能力及语言表达能力。 教学目标情感态度与价值观
体会在总结有理数加法法则的过程中与他人合作、交流的重要性,并且意识到数学与现实生活是紧密相连的.教学目标重点
有理数加法法则.
难点
异号两数相加的法则. 教学重难点 小刚在一条东西向的跑道上,先走了30米,又走了20米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米? 1.若两次都向东,一共向东走了多少米? (+30)+(+20)=+50+30 +20+502.若两次都向西,一共向西走了多少米? (-30)+(-20)=-50-20 -30-50 3.若第一次向东走20米,第二次向西走25米,那他现在在什么位置? (+20) +(-25) =-5 -25 +20-5 4.若第一次向西走25米,第二次向东走10米,那他现在在什么位置? (-25) +(+10) = -15 -25 +10-15 5.若第一次向西走20米,第二次向东走20米,那他现在在什么位置? (-20) +(+20) =0+20 -20 6.若第一次向东走30米,第二次站在原地没动,那他现在在什么位置? (+30) +0=+30+30+30有理数加法有没有规律? 1.和的符号与两个加数的符号有什么关系?
2.和的绝对值与两个加数的绝对值又有什么关系?想一想 观察、比较下面几个式子,看能否从这些算式中得到启发,想办法归纳出有理数加法的法则? (+30)+(+20)=+50
(-30)+(-20)=-50
(?20)+(?25)=?5
(?25)+ (?10)= ?15
(?20)+(?20)=0
(+30)+0=+30有理数加法法则:
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.知识要点例1:计算:
(1)(-4)+(-8);
(2)(-5)+13;
(3)0+(-7);
(4)(-4.7)+3.9.解:(1)(-4)+(-8)
=-(4+8)
=-12
(2)(-5)+13=+(13-8)=8
(3)0+(-7)=-7
(4)(-4.7)+4.7=-4.7+4.7=0 互为相反意义的量可以全部抵消或部分抵消. 例2:足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.分析: 解:每个队的进球总数记为正数,失球总数记为负数,这两数的和为这队的净胜球数。
三场比赛中,红球共进4球,失2球,净胜球数为
(+4)+(-2)=+(4-2)=2
黄队共进2球,失4球,净胜球为
(+2)+(-4)=-(4-2)=-2
篮球共进( )球,失( )球,净胜球数为( ).11(+1)+(-1)=0(1)16+(-12)___(-12)+16;
(2)(-19)+(-8)____(-8)+(-19);
(3)(-6.9)+1.5 ___1.5+(-6.9);
(4)0.5+(-5.9)___(-5.9)+0.5. 在横线上填上适当的符号,使两边的式子成立.====加法的交换律
有理数的加法中,两个数的加法,交换加数的位置,和不变.
即:a+b=b+a 1.式子中的字母分别表示任意的一个有理数。(如:既可成表示整数,也可以表示分数;既可以表示正数,也可以表示负数或0).
2.在同一个式子中,同一个字母表示同一个数.知识要点(1)[16+(-12)] +2_____16+ [(-12)+2]
(2)[(-19)+(-8)] +6____(-19)+ [(-8)+6]
(3)[(-6.9)+1.5] +9____(-6.9) + [1.5+9]
(4)[0.5+(-5.9)] +(-8)_____0.5+ [(-5.9)+(-8)]==== 在横线上填上适当的符号,使两边的式子成立.加法的结合律
有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
即:(a+b)+c =a+(b+c).知识要点例3:计算:
(1)24+(-12)+20+(-15);
(2)(-2.54)+3.56+(-7.46)+(-3.56).解(1)24+(-12)+20+(-15)
=24+20+[(-12)+(-15)]
=44+(-27)
=17 这里使用了哪些运算律 ? (2)(-2.54)+3.56+(-7.46)+(-3.56)
=[(-2.54)+(-7.46)] +[(+3.56)+
(-3.56)]
=(-10)+0
=-10.有理的加法常用的三个规律: 1. 一般地,总是先把正数或负数分别结合在一起相加. 2.有相反数的可先把相反数相加,能凑整的可先凑整. 3.有分母相同的,可先把分母相同的数结合相加.归纳 例4:每袋小麦的标准重量为90千克,10袋小麦称重记录如图所示。与标准重量比较,10袋小麦总计超过多少千克或不足多少千克?10袋小麦的总重量是多少? 解法1:先计算10袋小麦的总重量
91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1+91.1=905.4
再计算总计超过多少千克:
905.4-90×10=5.4 解法2:每袋小麦超过标准重量的千克数记作正数,不足的千克数记作负数。
10袋小麦对应的数为+1,+1,+1.5,-1,+1.2,+1.3, -1.3,-1.2,+1.8,+1.1。
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)
+1.8+1.1
=[1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)]+
(1+1.5+1.8+1.1)
=5.4
90×10+5.4=905.4答:10袋不麦一共905.4千克,总计超过5.4千克. 数扩展到有理数之后,下面这些结论还成立吗?请说明理由.
(1)若两个数的和是0,则这两个数都是0;
(2)任何两数相加,和不小于任何一个加数.议一议1.加法法则: (1)同号两数相加,取相同的符号,并把绝对值相加;若a>0,b>0,则a+b=+(|a|+|b|);
若a<0,b<0,则a+b=- (|a|+|b|). 课堂小结 (2)绝对值不相等的异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值; 若a>0,b<0,且|a|>|b|,则a+b=+(|a|-|b|)
若a>0,b<0,且|a|>|b|,则a+b=- (|b|+|a|)(3)互为相反数的两个数相加得0;若a>0,b<0,且|a|=|b|,则a+b=0;a+0=a.(4)一个数同0相加,仍得这个数.2.加法运算律(1)加法交换律:
a+b=b+a;
(2)加法结合律:
(a+b)+c=a+(b+c). 1.如果两个有理数的和为正数,则下列正确的是( )
A.两个数一定都是正数
B.两数都不为零
C.两个数中至少有一个为正数
D.两个数中至少有一个为负数 C随堂练习2.计算解: 3.已知|a|=2,|b|=3,求a+b的值. 解:因为|a|=2,|b|=3,
所以a=±2,b=±3
所以当a=2,b=3时,a+b=2+3=5
当a=2,b=-3时,a+b=2+(-3)=-1
当a=-2,b=3时,a+b=-2+3=1
当a=-2,b=-3时,a+b=-2+(-3)=-5.解: 5.仓库内原存粮食3500千克,一周内存入和取出情况如下(存入为正,单位:千克):-1500,2000,-800,700,-1000,1200,-240,问第七天末仓库内还存有多少粮食?解:
3500-1500+2000-800+700-1000+1200-240 =3860
答:第七天末仓库内还存有3860千克粮食.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
