18.1 勾股定理 课件3
图片预览



文档简介
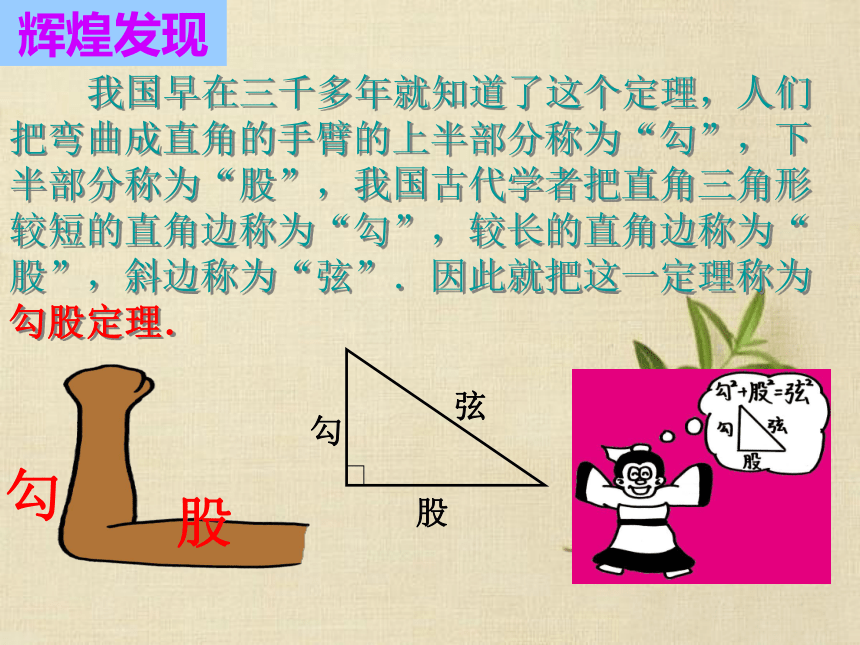
课件11张PPT。《18.1勾股定理》 我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
辉煌发现《周髀算经》 毕达哥拉斯 商高 数学史话《勾股圆方图》 ?(a + b)(b + a) = ?c2 + 2(?ab)
?a2 + ab + ?b2 = ?c2 + ab
? a2 + b2 = c2aabbcc证法1:伽菲尔德经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法.1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法.1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法.
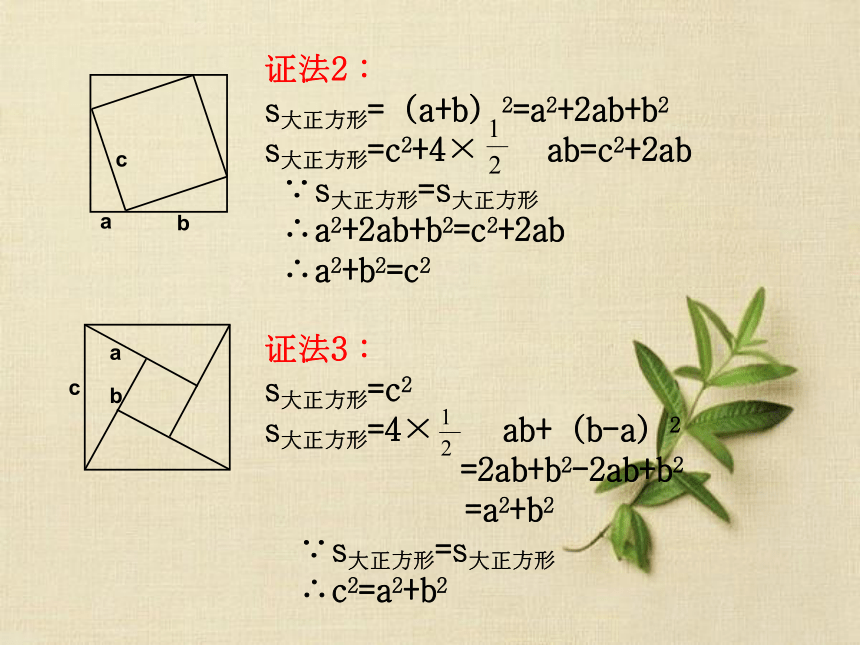
∟∟∟abcabc证法2:
s大正方形=(a+b)2=a2+2ab+b2
s大正方形=c2+4× ab=c2+2ab
∵s大正方形=s大正方形
∴a2+2ab+b2=c2+2ab
∴a2+b2=c2
证法3:
s大正方形=c2
s大正方形=4× ab+(b-a)2
=2ab+b2-2ab+b2
=a2+b2
∵s大正方形=s大正方形
∴c2=a2+b2 定理:经过证明被确认为正确的命题叫做定理. 勾股定理:如果直角三角形的两直角边长分别为a、b,斜边为c,那么a2+b2=c2.1、如图,一个高3米,宽4米的大门,需在相对角的顶点间加一个加固木条,则木条的长为. ( )A.3 米 B.4 米 C.5米 D.6米C34基础练习之出谋划策2、求出下列直角三角形中未知边的长度.解:由勾股定理得:x2 =36+64x2 =100x2=62+82∴ x=10∵ x2+52=132∴ x2=132-52x2 =169-25x2 =144∴ x=12∵ x > 0∵ x > 0例、如图,在Rt△ABC中,∠C=90°,AD平分∠BAC, AC=6cm,BC=8cm,(1)求线段CD的长;(2)求△ABD的面积.xx8-x664方程思想:直角三角形中,已知一条边,以及另外两条边的数量关系时,可利用勾股定理建立方程求解. 810S△ABC=84或36补充练习:
1、在△ABC中,AD是BC边上的高,若AB=l0,AD=8,AC=17,求△ABC的面积.小结:勾股定理在生活中的应用十分广泛,利用勾股定理解决问题,关键是找出问题中隐藏的直角三角形或自己构造合适的直角三角形,尝试把立体图形转换为平面图形.
辉煌发现《周髀算经》 毕达哥拉斯 商高 数学史话《勾股圆方图》 ?(a + b)(b + a) = ?c2 + 2(?ab)
?a2 + ab + ?b2 = ?c2 + ab
? a2 + b2 = c2aabbcc证法1:伽菲尔德经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法.1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法.1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法.
∟∟∟abcabc证法2:
s大正方形=(a+b)2=a2+2ab+b2
s大正方形=c2+4× ab=c2+2ab
∵s大正方形=s大正方形
∴a2+2ab+b2=c2+2ab
∴a2+b2=c2
证法3:
s大正方形=c2
s大正方形=4× ab+(b-a)2
=2ab+b2-2ab+b2
=a2+b2
∵s大正方形=s大正方形
∴c2=a2+b2 定理:经过证明被确认为正确的命题叫做定理. 勾股定理:如果直角三角形的两直角边长分别为a、b,斜边为c,那么a2+b2=c2.1、如图,一个高3米,宽4米的大门,需在相对角的顶点间加一个加固木条,则木条的长为. ( )A.3 米 B.4 米 C.5米 D.6米C34基础练习之出谋划策2、求出下列直角三角形中未知边的长度.解:由勾股定理得:x2 =36+64x2 =100x2=62+82∴ x=10∵ x2+52=132∴ x2=132-52x2 =169-25x2 =144∴ x=12∵ x > 0∵ x > 0例、如图,在Rt△ABC中,∠C=90°,AD平分∠BAC, AC=6cm,BC=8cm,(1)求线段CD的长;(2)求△ABD的面积.xx8-x664方程思想:直角三角形中,已知一条边,以及另外两条边的数量关系时,可利用勾股定理建立方程求解. 810S△ABC=84或36补充练习:
1、在△ABC中,AD是BC边上的高,若AB=l0,AD=8,AC=17,求△ABC的面积.小结:勾股定理在生活中的应用十分广泛,利用勾股定理解决问题,关键是找出问题中隐藏的直角三角形或自己构造合适的直角三角形,尝试把立体图形转换为平面图形.
