18.2 勾股定理的逆定理 课件2

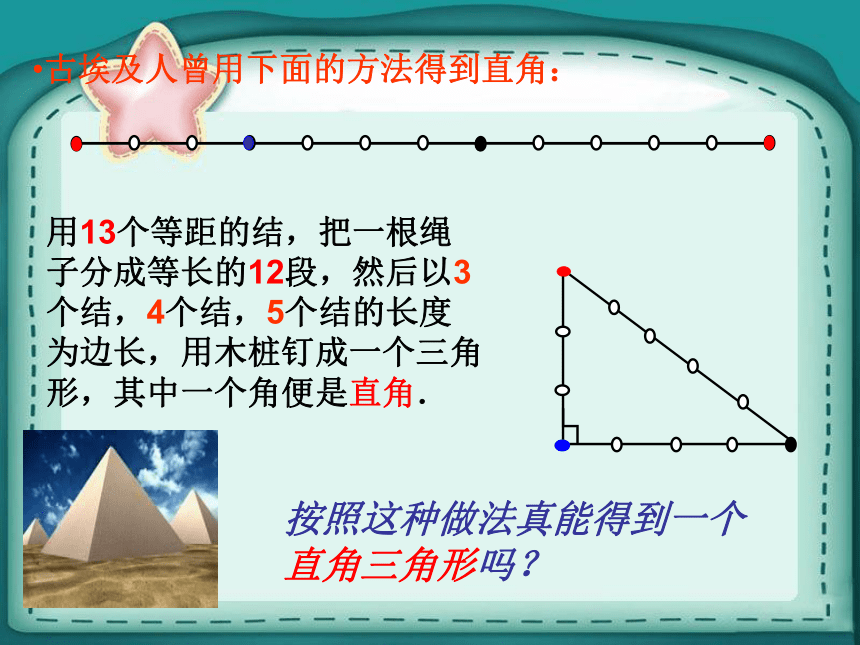
课件9张PPT。 18．2勾股定理的逆定理古埃及人曾用下面的方法得到直角.按照这种做法真能得到一个直角三角形吗？ 古埃及人曾用下面的方法得到直角：用13个等距的结，把一根绳子分成等长的12段，然后以3个结，4个结，5个结的长度为边长，用木桩钉成一个三角形，其中一个角便是直角．
下面的三组数分别是一个三角形的三边长a，b，c：5，12，13； 7，24，25； 8，15，17．动手画一画勾股定理的逆定理 如果三角形的三边长a，b，c满足
a2+b2=c2，
那么这个三角形是直角三角形．
说明：（1）一般地，如果一个定理的逆命题经过证明是正确的，它也是一个定理，称这两个定理为互逆定理；
（2）勾股定理主要反映了直角三角形三边之间的数量关系，它是解决直角三角形中有关计算与证明的主要依据；
（3）勾股定理的逆定理主要的应用是把数转化为形，通过计算三角形三边之间的关系来判断一个三角形是否是直角三角形，它可作为直角三角形的判定依据．练习1．如果三条线段长a，b，c满足a2=c2-b2，这三条线段组成的三角形是不是直角三角形？为什么？
2．以下各组数为边长，能组成直角三角形的是（ ）．
A．5，6，7 B．10，8，4
C．7，25，24 D．9，17，15
3．以下各组正数为边长，能组成直角三角形的是（ ）．
A．a-1，2a，a+1 B．a-1，2 ，a+1
C．a-1， ，a+1 D．a-1， a，a+14 ．古希腊的哲学家柏拉图曾指出，如果m表示大于1的整数，a=2m，b=m2-1，c=m2+1，那么a，b，c为勾股数．你认为对吗？如果对，你能利用这个结论得出一些勾股数吗？练习例题例1 判断由线段a，b，c组成的三角形是不是直角三角形：
（1）a=15，b=8，c=17；
（2）a=13，b=14，c=15．课堂小结1．勾股定理的逆定理及其作用；
2．勾股定理的逆定理在生活中的应用