18.2 勾股定理的逆定理 课件5
图片预览






文档简介
课件14张PPT。18.2 勾股定理的逆定理回忆1. 直角三角形有哪些性质?
(1)两个锐角互余;
(2)两直角边的平方和等于斜边的平方;
(3)在含30°角的直角三角形中,30°
的角所对的直角边是斜边的一半2. 一个三角形,满足什么条件是直角三角形?有一个内角是90°,那么这个三角形就为直角三角形.如果一个三角形中,有两个角的和是90°,那么这
个三角形也是直角三角形.我们是否可以不用角,而用三角形三边的关系
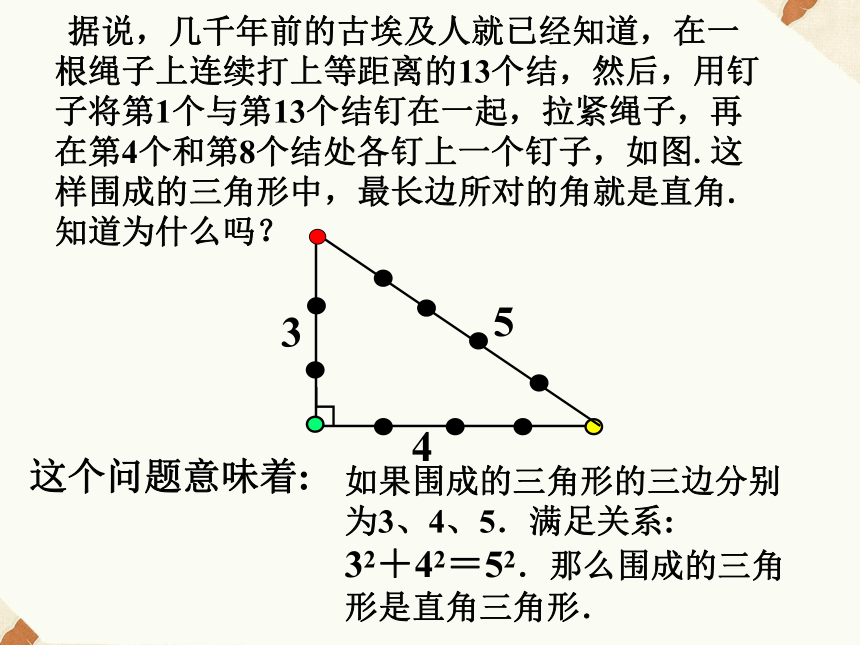
来判断是否为直角三角形呢? 据说,几千年前的古埃及人就已经知道,在一根绳子上连续打上等距离的13个结,然后,用钉子将第1个与第13个结钉在一起,拉紧绳子,再在第4个和第8个结处各钉上一个钉子,如图.这样围成的三角形中,最长边所对的角就是直角.知道为什么吗?这个问题意味着:如果围成的三角形的三边分别为3、4、5.满足关系: 32+42=52.那么围成的三角形是直角三角形.猜想: 如果三角形的三边长a,b,c有关系a2+b2=c2, 那么这个三角形是直角三角形.
大家想想,这个猜想与勾股定理有何关系?
请解释……做一做用圆规、直尺作△ABC,使AB=5cm,AC=4cm,BC=3cm,量一量∠C,它是90°吗?∠C是直角吗?如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.可见:这是判定直角三角形的根据之一.∵AC2+BC2=AB2(已知),
∴△ABC是直角三角形(勾股定理的逆定理).你能用语言来叙述一下刚才的定理吗?勾股定理的逆定理
例1 根据下列三角形的三边a、b、c的值,判断三角形是不是直角三角形.如果是,指出哪条边所对的角是直角?
(1)a=7,b=24,c=25;
(2)a=7,b=8,c=11.解(1)∵最大边是c=25,c2=625,
a2+b2=72+242=625,∴a2+b2=c2,
∴△ABC是直角三角形,最大边c所对的角是直角.
(2)∵最大边是c=11,c2=121,
a2+b2=72+82 =113,
∴a2+b2≠c2 .
∴△ABC不是直角三角形.例2 已知:在△ABC中,三条边长分别为a=n2-1,b=2n,c=n2+1(n>1).求证:△ABC为直角三角形.证明
∴△ABC是直角三角形.(勾股定理的逆定理)能够成为直角三角形三条边长度的三个正整数,称为勾股数.练习:
1.小蒋要求△ABC的的最长边上的高,测得AB=8cm,
AC=6cm,BC=10cm.则可知最长边上的高_______ 4.8cm2. 满足下列条件的△ABC,不是直角三角形的是( )
A.b2=a2-c2 B. a:b:c=3:4:5
C.∠C=∠A-∠B D. ∠A:∠B : ∠C =3:4:5D3.在下列长度的各组线段中,能组成直角三角形的是( )
A. 5,6,7 B. 32,42,52 C. 5,11,12 D. 5,12,13D5.将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( )钝角三角形; B. 锐角三角形;
C. 直角三角形; D. 等腰三角形. 6.已知一个三角形的三边长分别是12cm,16cm,20cm,你能计算出这个三角形的面积吗? 4.在ΔABC中,若AB2+BC2=AC2,则∠A+∠C= ° . 课堂小结:1.勾股定理的逆定理的功能是什么?
2.截止到目前为止,你有哪些方法判定直角三角形?
3.若一个题目告诉你一个直角三角形的两边长,接下来你会用什么?干什么?
4.若一个题目告诉你一个三角形的三边长,你会想到哪些? 布置作业
课堂作业:P59练习;
家庭作业 : (1)P60习题第2、3题;
(2)预习下一节内容. 教学反思
(1)两个锐角互余;
(2)两直角边的平方和等于斜边的平方;
(3)在含30°角的直角三角形中,30°
的角所对的直角边是斜边的一半2. 一个三角形,满足什么条件是直角三角形?有一个内角是90°,那么这个三角形就为直角三角形.如果一个三角形中,有两个角的和是90°,那么这
个三角形也是直角三角形.我们是否可以不用角,而用三角形三边的关系
来判断是否为直角三角形呢? 据说,几千年前的古埃及人就已经知道,在一根绳子上连续打上等距离的13个结,然后,用钉子将第1个与第13个结钉在一起,拉紧绳子,再在第4个和第8个结处各钉上一个钉子,如图.这样围成的三角形中,最长边所对的角就是直角.知道为什么吗?这个问题意味着:如果围成的三角形的三边分别为3、4、5.满足关系: 32+42=52.那么围成的三角形是直角三角形.猜想: 如果三角形的三边长a,b,c有关系a2+b2=c2, 那么这个三角形是直角三角形.
大家想想,这个猜想与勾股定理有何关系?
请解释……做一做用圆规、直尺作△ABC,使AB=5cm,AC=4cm,BC=3cm,量一量∠C,它是90°吗?∠C是直角吗?如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.可见:这是判定直角三角形的根据之一.∵AC2+BC2=AB2(已知),
∴△ABC是直角三角形(勾股定理的逆定理).你能用语言来叙述一下刚才的定理吗?勾股定理的逆定理
例1 根据下列三角形的三边a、b、c的值,判断三角形是不是直角三角形.如果是,指出哪条边所对的角是直角?
(1)a=7,b=24,c=25;
(2)a=7,b=8,c=11.解(1)∵最大边是c=25,c2=625,
a2+b2=72+242=625,∴a2+b2=c2,
∴△ABC是直角三角形,最大边c所对的角是直角.
(2)∵最大边是c=11,c2=121,
a2+b2=72+82 =113,
∴a2+b2≠c2 .
∴△ABC不是直角三角形.例2 已知:在△ABC中,三条边长分别为a=n2-1,b=2n,c=n2+1(n>1).求证:△ABC为直角三角形.证明
∴△ABC是直角三角形.(勾股定理的逆定理)能够成为直角三角形三条边长度的三个正整数,称为勾股数.练习:
1.小蒋要求△ABC的的最长边上的高,测得AB=8cm,
AC=6cm,BC=10cm.则可知最长边上的高_______ 4.8cm2. 满足下列条件的△ABC,不是直角三角形的是( )
A.b2=a2-c2 B. a:b:c=3:4:5
C.∠C=∠A-∠B D. ∠A:∠B : ∠C =3:4:5D3.在下列长度的各组线段中,能组成直角三角形的是( )
A. 5,6,7 B. 32,42,52 C. 5,11,12 D. 5,12,13D5.将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( )钝角三角形; B. 锐角三角形;
C. 直角三角形; D. 等腰三角形. 6.已知一个三角形的三边长分别是12cm,16cm,20cm,你能计算出这个三角形的面积吗? 4.在ΔABC中,若AB2+BC2=AC2,则∠A+∠C= ° . 课堂小结:1.勾股定理的逆定理的功能是什么?
2.截止到目前为止,你有哪些方法判定直角三角形?
3.若一个题目告诉你一个直角三角形的两边长,接下来你会用什么?干什么?
4.若一个题目告诉你一个三角形的三边长,你会想到哪些? 布置作业
课堂作业:P59练习;
家庭作业 : (1)P60习题第2、3题;
(2)预习下一节内容. 教学反思
