24.2.3 圆心角、弧、弦、弦心距之间的关系 课件3
文档属性
| 名称 | 24.2.3 圆心角、弧、弦、弦心距之间的关系 课件3 |

|
|
| 格式 | zip | ||
| 文件大小 | 356.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-19 13:51:51 | ||
图片预览

文档简介
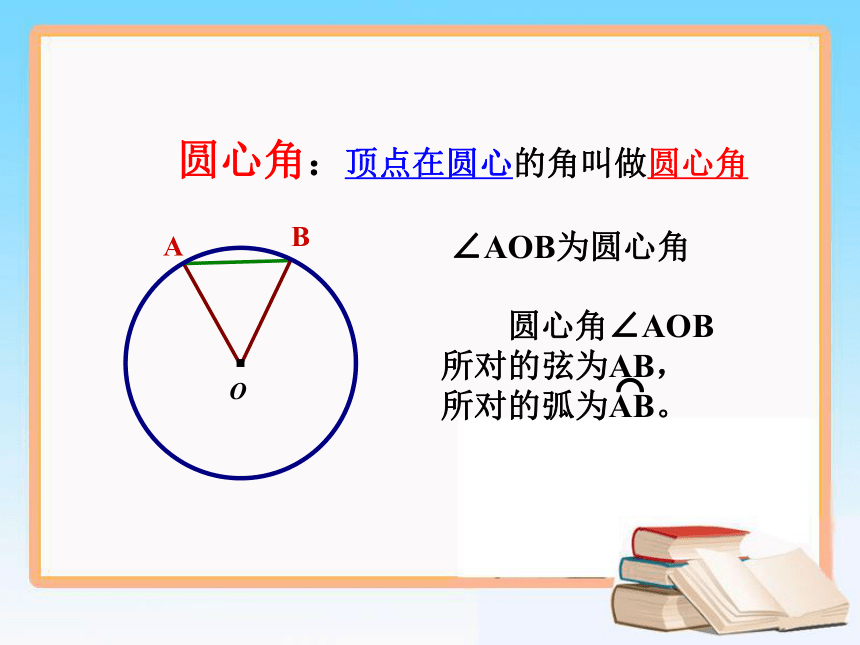
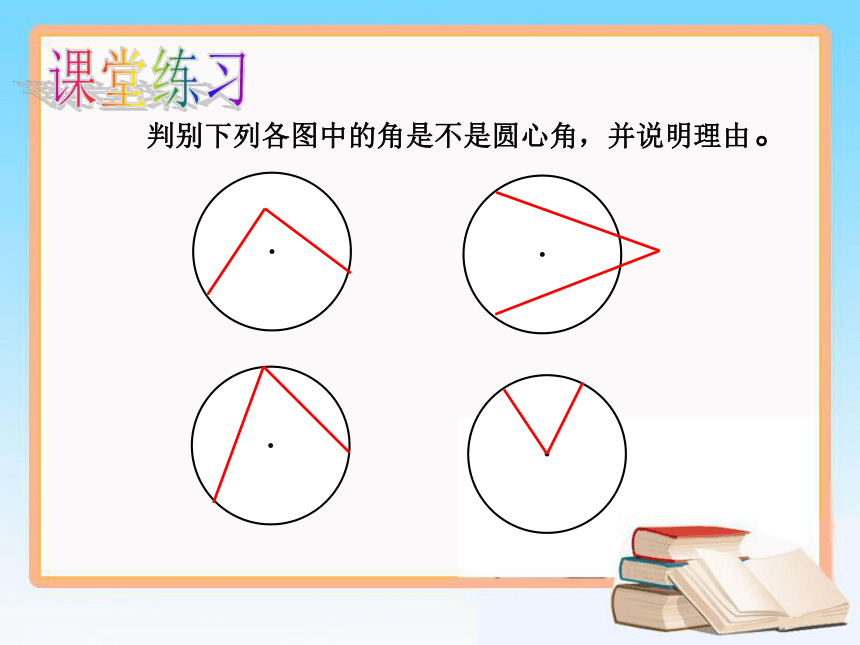
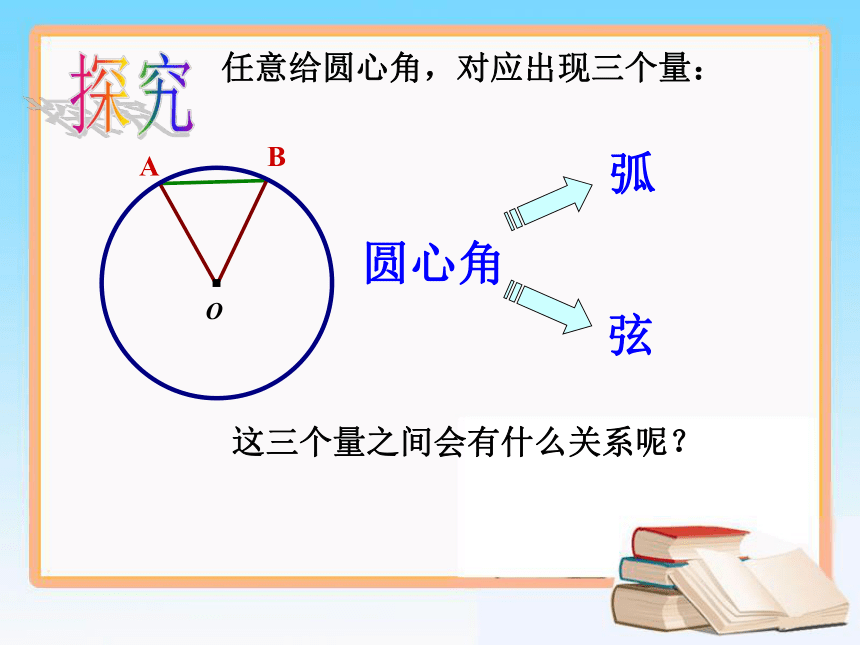
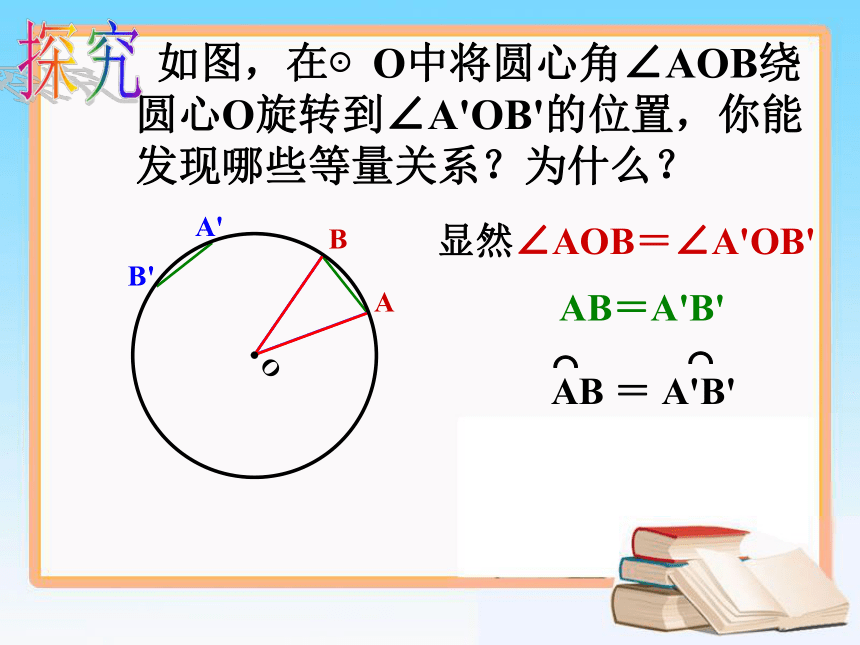
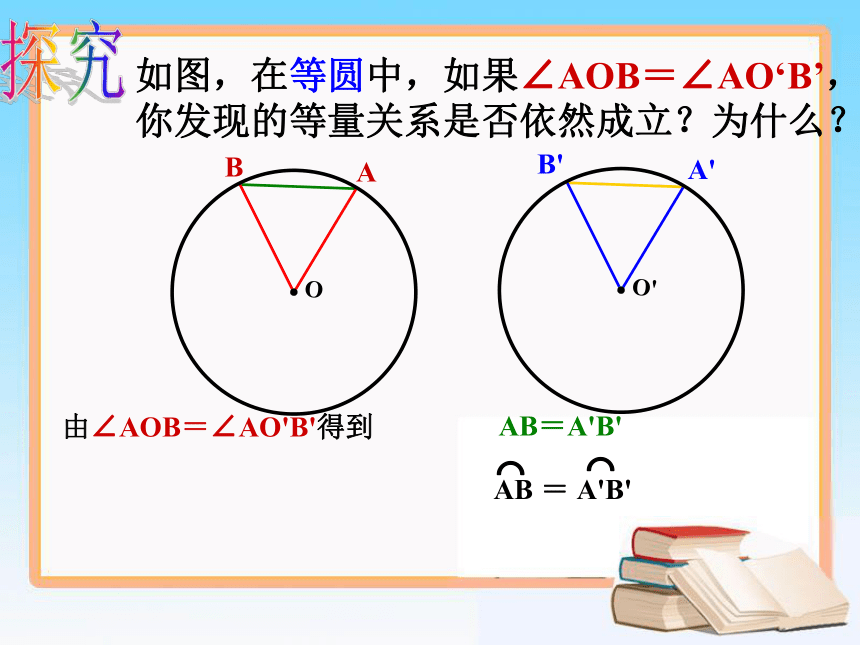
课件16张PPT。24.2.3 弧、弦、圆心角圆是中心对称图形吗?它的对称中心在哪里?·圆是中心对称图形它的对称中心是圆心圆心角:顶点在圆心的角叫做圆心角∠AOB为圆心角判别下列各图中的角是不是圆心角,并说明理由。课堂练习任意给圆心角,对应出现三个量:圆心角这三个量之间会有什么关系呢?探究BA 如图,在⊙O中将圆心角∠AOB绕圆心O旋转到∠A'OB'的位置,你能发现哪些等量关系?为什么?显然∠AOB=∠A'OB' AB=A'B'探究AB=A'B'如图,在等圆中,如果∠AOB=∠AO‘B’,你发现的等量关系是否依然成立?为什么?由∠AOB=∠AO'B'得到探究圆心角定理 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等. 定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?同样,还可以得到:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角_____, 所对的弦________;
在同圆或等圆中,如果两条弦相等,那么他们所对的圆心角______,所对的弧_________. 同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.等对等定理① 圆心角
弧
③ 弦知一得二等对等定理整体理解如图,AB、CD是⊙O的两条弦。
(1)如果AB=CD,那么 , 。
(2)如果AB=CD,那么 , 。
(3)如果∠AOB=∠COD,那么 , 。
(4)如果AB=CD,OE⊥AB,OF⊥CD,OE与OF相等吗?为什么?课堂练习 已知:在⊙O中,AB =AC∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.⌒ ⌒课堂练习 如图,AB是⊙O的直径,BC=CD=DE,∠COD=35°,求∠AOE的度数。⌒⌒⌒课堂练习 在同圆或等圆中,相等的圆心角,所对的弦的弦心距相等吗?① 圆心角
② 弧
③ 弦
④弦心距知一得三1、四个元素:
圆心角、弦、弧、弦心距2、四个相等关系:课堂小结① 圆心角
② 弧
弦
④弦心距 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角_____, 所对的弦________;
在同圆或等圆中,如果两条弦相等,那么他们所对的圆心角______,所对的弧_________. 同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.等对等定理① 圆心角
弧
③ 弦知一得二等对等定理整体理解如图,AB、CD是⊙O的两条弦。
(1)如果AB=CD,那么 , 。
(2)如果AB=CD,那么 , 。
(3)如果∠AOB=∠COD,那么 , 。
(4)如果AB=CD,OE⊥AB,OF⊥CD,OE与OF相等吗?为什么?课堂练习 已知:在⊙O中,AB =AC∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.⌒ ⌒课堂练习 如图,AB是⊙O的直径,BC=CD=DE,∠COD=35°,求∠AOE的度数。⌒⌒⌒课堂练习 在同圆或等圆中,相等的圆心角,所对的弦的弦心距相等吗?① 圆心角
② 弧
③ 弦
④弦心距知一得三1、四个元素:
圆心角、弦、弧、弦心距2、四个相等关系:课堂小结① 圆心角
② 弧
弦
④弦心距 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
