2.1.4 多项式的乘法 课件1
图片预览








文档简介
课件25张PPT。整式的乘法2.1——2.1.4 多项式的乘法怎样计算单项式2x与多项式3x2-x-5的积?可以运用乘法对加法的分配律. 2x·(3x2-x -5 )
= 2x·3x2 + 2x·(-x)+2x·(-5)
= 6x3 -2x2 -10x . 一般地,单项式与多项式相乘,先用单项式乘多项式中的每一项,再把所得的积相加.举
例例10 计算:解:举
例例11 求
的值,其中x=2,y=-1.当 x=2,y=-1时,原式的值为
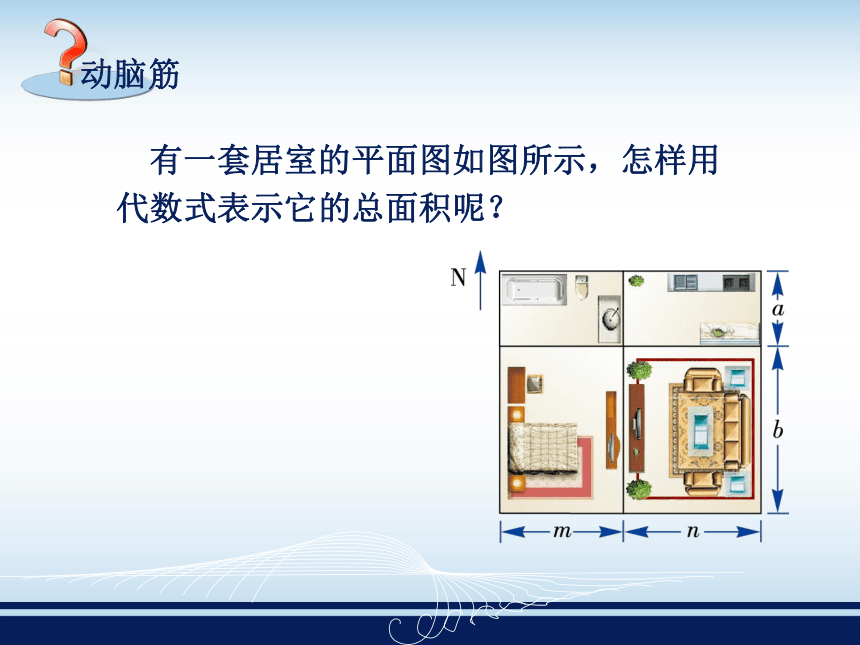
3×23×(-1) +2×22×(-1)2 = -24+8 = -16. 有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?南北向总长为a+b东西向总长为m+n所以居室的总面积为:(a+b)·(m+n); ①北边两间房的面积和为a(m+n)南边两间房的面积和为b(m+n)所以居室的总面积为:a(m+n)+b(m+n) ②四间房(厅)的面积分别为am,an,bm,bn所以居室的总面积为:am+an+bm+bn ③这三个代数式之间有什么关系呢? (a+b)·(m+n) ① a(m+n)+b(m+n) ② am+an+bm+bn ③ 上面三个代数式都正确表示了该居室的总面积,因此有(a+b)(m+n)= a(m+n)+b(m+n)
= am+an+bm+bn. 撇开上述式子的实际意义,想一想,这几个代数式为什么相等呢? 它们利用了乘法运算的什么性质? 事实上,由代数式①到代数式②,是把m+n看成一个整体,利用乘法分配律得到a(m+n)+b(m+n),继续利用乘法分配律,就得到结果am + an + bm+bn. 一般地,多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加.举
例例12 计算:
(1)(2x+y)(x-3y);
(2)( 2x+1)(3x2-x-5);
(3)(x+a)(x+b). (1) (2x+y)(x-3y)解 (2x+y)(x-3y)= 2x · x + 2x ·(-3y)+ y · x + y ·(-3y)= 2x2-6xy+yx-3y2= 2x2-5xy-3y2(2) ( 2x+1)(3x2-x-5);解 (2x+1)(3x2-x-5)= 6x3-2x2–10x+3x2 -x-5= 6x3 + x2-11x - 5.解 (x+a)(x+b)= x2+bx+ax+ab=x2+(a+b)x +ab(3)(x+a)(x+b)第(3)小题的直观意义如图举
例例13 计算:
(1)(a+b)(a-b);
(2)(a+b)2 ;
(3)(a-b)2.解(1)(a+b)(a-b)= a2-ab+ba-b2= a2-b2= (a+b)(a+b)= a2+ab+ba+b2 (2) (a+b)2= a2+2ab+b2= (a-b)(a-b)= a2-ab-ba+b2 (3) (a-b)2= a2-2ab+b2 计算:(a2+3)(a-2)-a(a2-2a-2).结 束
= 2x·3x2 + 2x·(-x)+2x·(-5)
= 6x3 -2x2 -10x . 一般地,单项式与多项式相乘,先用单项式乘多项式中的每一项,再把所得的积相加.举
例例10 计算:解:举
例例11 求
的值,其中x=2,y=-1.当 x=2,y=-1时,原式的值为
3×23×(-1) +2×22×(-1)2 = -24+8 = -16. 有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?南北向总长为a+b东西向总长为m+n所以居室的总面积为:(a+b)·(m+n); ①北边两间房的面积和为a(m+n)南边两间房的面积和为b(m+n)所以居室的总面积为:a(m+n)+b(m+n) ②四间房(厅)的面积分别为am,an,bm,bn所以居室的总面积为:am+an+bm+bn ③这三个代数式之间有什么关系呢? (a+b)·(m+n) ① a(m+n)+b(m+n) ② am+an+bm+bn ③ 上面三个代数式都正确表示了该居室的总面积,因此有(a+b)(m+n)= a(m+n)+b(m+n)
= am+an+bm+bn. 撇开上述式子的实际意义,想一想,这几个代数式为什么相等呢? 它们利用了乘法运算的什么性质? 事实上,由代数式①到代数式②,是把m+n看成一个整体,利用乘法分配律得到a(m+n)+b(m+n),继续利用乘法分配律,就得到结果am + an + bm+bn. 一般地,多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加.举
例例12 计算:
(1)(2x+y)(x-3y);
(2)( 2x+1)(3x2-x-5);
(3)(x+a)(x+b). (1) (2x+y)(x-3y)解 (2x+y)(x-3y)= 2x · x + 2x ·(-3y)+ y · x + y ·(-3y)= 2x2-6xy+yx-3y2= 2x2-5xy-3y2(2) ( 2x+1)(3x2-x-5);解 (2x+1)(3x2-x-5)= 6x3-2x2–10x+3x2 -x-5= 6x3 + x2-11x - 5.解 (x+a)(x+b)= x2+bx+ax+ab=x2+(a+b)x +ab(3)(x+a)(x+b)第(3)小题的直观意义如图举
例例13 计算:
(1)(a+b)(a-b);
(2)(a+b)2 ;
(3)(a-b)2.解(1)(a+b)(a-b)= a2-ab+ba-b2= a2-b2= (a+b)(a+b)= a2+ab+ba+b2 (2) (a+b)2= a2+2ab+b2= (a-b)(a-b)= a2-ab-ba+b2 (3) (a-b)2= a2-2ab+b2 计算:(a2+3)(a-2)-a(a2-2a-2).结 束
