2.1.4 多项式的乘法 课件2

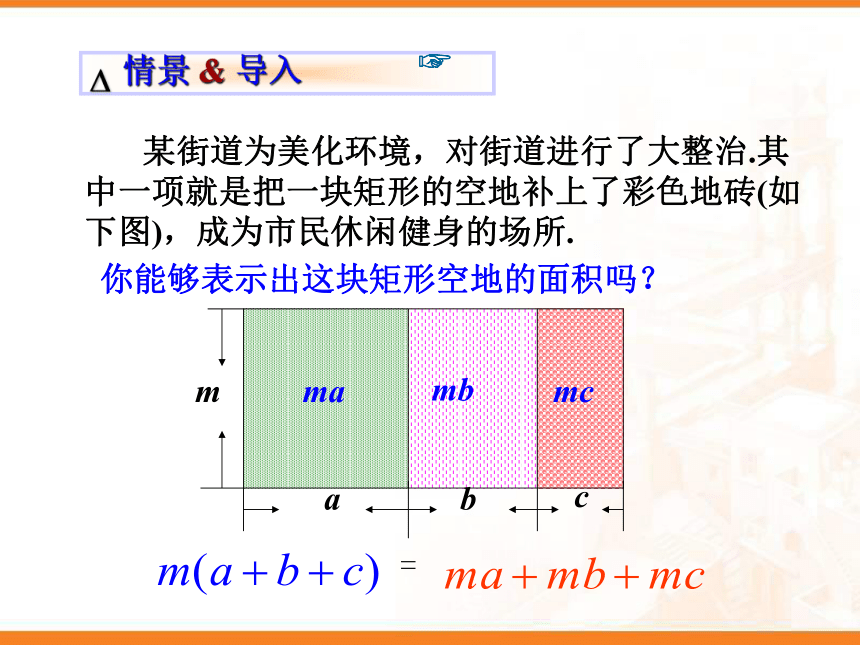
课件26张PPT。 2.1.4 多项式的乘法 如何进行单项式乘单项式的运算？单项式的系数？相同字母的幂？只在一个单项式里含有的字母？单项式与单项式相乘： 单×单＝(系数×系数)(同底数幂×同底数幂)(单独的幂) ( 2a2b3c) (-3ab)= -6a3b4cmabcmambmc 某街道为美化环境，对街道进行了大整治.其中一项就是把一块矩形的空地补上了彩色地砖(如下图)，成为市民休闲健身的场所.你能够表示出这块矩形空地的面积吗？=一般地，单项式与多项式相乘，只要将单项式分别乘以多项式的各项，再将所得的积相加如图，在长方形地块上建造住宅、广场、商厦，计算这块地的面积．解：长方形地块的长为（3a+2b）+（2a-b）、宽为4a，这块地的面积为4a·[（3a+2b）+（2a-b）]
=4a·（5a+b）
=4a·5a+4a·b
=20a2+4ab.答：这块地的面积为20a2+4ab.例10 计算：当 x=2，y=-1时，原式的值为
3×23×(-1) +2×22×(-1)2 = -24+8 = -16.回顾与思考② 再把所得的积相加.① 将单项式分别乘以多项式的各项，进行单项式与多项式乘法运算时，要注意什么？① 不能漏乘:即单项式要乘遍多项式的每一项.② 去括号时注意符号的确定.某地区在退耕还林期间，有一块原长m米，宽
为a米的长方形林区增长了n米，加宽了b米，
请你表示这块林区现在的面积.manambnb你能用不同的形式表示所拼图的面积吗？这块林区现在长为（m+n）米，宽为（a+b）米.因而面积为(m+n)(a+b)米2. 由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积，故有：
(m+n)(a+b)=ma+ mb+ na+ nb如何进行多项式与多项式相乘的运算？(a+b)(m+n)=am1234+an+bm+bn多项式的乘法法则例12 计算：
(1)(2x+y)(x-3y)；
(2)( 2x+1)(3x2-x-5)；
(3)(x+a)(x+b). (1) (2x+y)(x-3y)解 (2x+y)(x-3y)= 2x · x + 2x ·(-3y)+ y · x + y ·(-3y)= 2x2-6xy+yx-3y2= 2x2-5xy-3y2(2) ( 2x+1)(3x2-x-5)；解 (2x+1)(3x2-x-5)= 6x3-2x2–10x+3x2 -x-5= 6x3 + x2-11x - 5．解 (x+a)(x+b)= x2+bx+ax+ab=x2+(a+b)x +ab(3)(x+a)(x+b)例13 计算：
(1)(a+b)(a-b)；
(2)(a+b)2 ；
(3)(a-b)2.解(1)(a+b)(a-b)= a2-ab+ba-b2= a2-b2= (a+b)(a+b)= a2+ab+ba+b2 (2) (a+b)2= a2+2ab+b2= (a-b)(a-b)= a2-ab-ba+b2 (3) (a-b)2= a2-2ab+b2计算：(x+y )( x2-xy+y2) -x2y+=x3xy2+x2y-xy2+y3=x3+y3.练一练： 1.计算：
（1）（x+2）（x-3）；（2）（3x-1）（x-2）.解：课外练习 2.计算：
（1）（3m+n）（m-2n）；（2）n（n+1）（n+2）.解：3.计算： (1)(x?3y)(x+7y)， (2)(2x + 5y)(3x?2y).+7xy-3yx-=x2 +4xy-21y2； 21y2（2） (2x +5 y)(3x?2y)==x22x?3x ?2x? 2y +5 y? 3x-5y?2y=6x2?4xy+ 15xy-10y2=6x2 +11xy-10y2.挑战极限： 如果(x2+bx+8)(x2 – 3x+c)的乘积中不含x2和x3的项，求b、c的值.解：原式= x4 – 3x3 + c x2 +bx3
– 3bx2 +bcx+8x2– 24x+8cx2项系数为：c –3b+8x3项系数为：b – 3= 0= 0∴ b=3 ， c=1.