2.2.2 完全平方公式 课件
图片预览







文档简介
课件22张PPT。2.2.2 完全平方公式计算下列各式,你能发现怎样的规律?(a+b)2=a2+2ab+b2,我们把(a-b)2=a2-2ab+b2.都叫做完全平方公式. 两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍. 也就是:你觉得这个公式有什么特征?在使用这个公式时应该注意什么?是相同的两个二项多项式的乘积首先确定好谁是公式中的a和b,
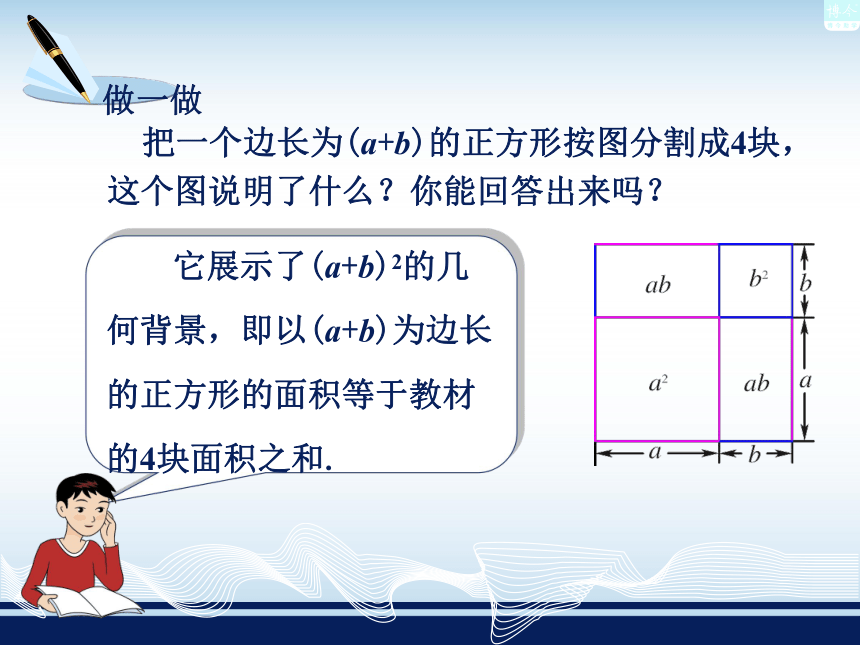
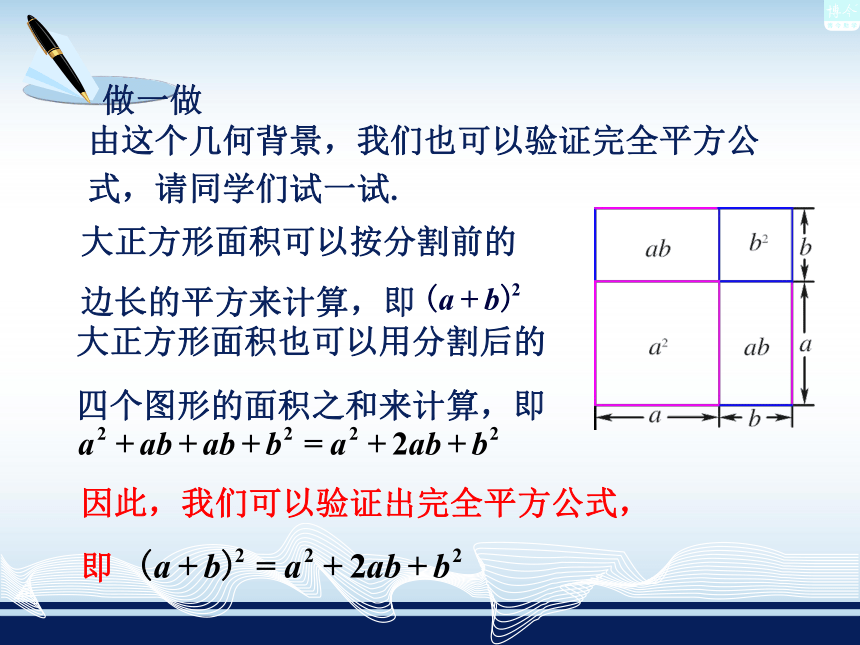
然后带着a和b的符号套用完全平方公式总结出完全平方公式对我们有什么帮助?可以使我们在计算这种类型的多项式乘法时更加快速和简便你能利用完全平方公式快速地计算出(2x+y)2吗?可以这样算!(a+b)2=a2+2ab+b2. 把2x与y分别看成上式的a与b,也就是把它们按下面的方法对应起来,就可以直接得到结果. ( 2x + y )2 ( + )2a b = ( )2 + · ( )· + 2 2x22x yy= 4x2+4xy+y2, = a 2 + 2 · a · b + b 2 . 可以用类似的方法直接得到(2x-y)2的结果吗? ( 2x -y )2= 4x2-4xy+y2 把一个边长为(a+b)的正方形按图分割成4块,这个图说明了什么?你能回答出来吗? 它展示了(a+b)2的几何背景,即以(a+b)为边长的正方形的面积等于教材的4块面积之和.由这个几何背景,我们也可以验证完全平方公式,请同学们试一试.例4 运用完全平方公式计算:
(1)(3m+n)2;
(2)(1)(3m+n)2 解 (3m+n)2= (3m)2+2 · 3m · n + n2= 9m2+6mn+n2.解1. (a-b)2与(b-a)2有什么关系?2. (a+b)2与(-a-b)2有什么关系?答:相等.
这是因为 (b-a)2 = [-(a-b)]2=(a-b)2.答:相等.
这是因为 (-a-b)2
= [-(a+b)]2=(a+b)2.例5 运用完全平方公式计算:
(1)(-x+1)2;
(2)(-2x-3)2.(1)(-x+1)2解 (-x+1)2= (-x)2+2(-x)· 1 + 12= x2-2x+1这个题还可以这样做:
(-x+1)2 =(1-x)2
= 12-2 · 1 · x +x2
= 1-2x+x2. (2) (-2x-3)2解 (-2x-3)2= [-(2x+3)]2= (2x+3)2= 4x2+12x+9.(1)例7 运用完全平方公式计算:
(1)1042;
(2)1982.(1) 1042解 1042= (100+4)2= 1002+2×100×4+42= 10 000+800+16= 10 816.(2) 1982解 1982= (200-2)2= 2002-2×200×2+22= 40 000-800+4= 39 204.课外练习本节课我们学习了什么知识?从本节课探索公式的过程中,你有怎样的收获?本节课我们学习的公式在使用时应注意哪些问题?
然后带着a和b的符号套用完全平方公式总结出完全平方公式对我们有什么帮助?可以使我们在计算这种类型的多项式乘法时更加快速和简便你能利用完全平方公式快速地计算出(2x+y)2吗?可以这样算!(a+b)2=a2+2ab+b2. 把2x与y分别看成上式的a与b,也就是把它们按下面的方法对应起来,就可以直接得到结果. ( 2x + y )2 ( + )2a b = ( )2 + · ( )· + 2 2x22x yy= 4x2+4xy+y2, = a 2 + 2 · a · b + b 2 . 可以用类似的方法直接得到(2x-y)2的结果吗? ( 2x -y )2= 4x2-4xy+y2 把一个边长为(a+b)的正方形按图分割成4块,这个图说明了什么?你能回答出来吗? 它展示了(a+b)2的几何背景,即以(a+b)为边长的正方形的面积等于教材的4块面积之和.由这个几何背景,我们也可以验证完全平方公式,请同学们试一试.例4 运用完全平方公式计算:
(1)(3m+n)2;
(2)(1)(3m+n)2 解 (3m+n)2= (3m)2+2 · 3m · n + n2= 9m2+6mn+n2.解1. (a-b)2与(b-a)2有什么关系?2. (a+b)2与(-a-b)2有什么关系?答:相等.
这是因为 (b-a)2 = [-(a-b)]2=(a-b)2.答:相等.
这是因为 (-a-b)2
= [-(a+b)]2=(a+b)2.例5 运用完全平方公式计算:
(1)(-x+1)2;
(2)(-2x-3)2.(1)(-x+1)2解 (-x+1)2= (-x)2+2(-x)· 1 + 12= x2-2x+1这个题还可以这样做:
(-x+1)2 =(1-x)2
= 12-2 · 1 · x +x2
= 1-2x+x2. (2) (-2x-3)2解 (-2x-3)2= [-(2x+3)]2= (2x+3)2= 4x2+12x+9.(1)例7 运用完全平方公式计算:
(1)1042;
(2)1982.(1) 1042解 1042= (100+4)2= 1002+2×100×4+42= 10 000+800+16= 10 816.(2) 1982解 1982= (200-2)2= 2002-2×200×2+22= 40 000-800+4= 39 204.课外练习本节课我们学习了什么知识?从本节课探索公式的过程中,你有怎样的收获?本节课我们学习的公式在使用时应注意哪些问题?
