5.1.2 轴对称变换 课件

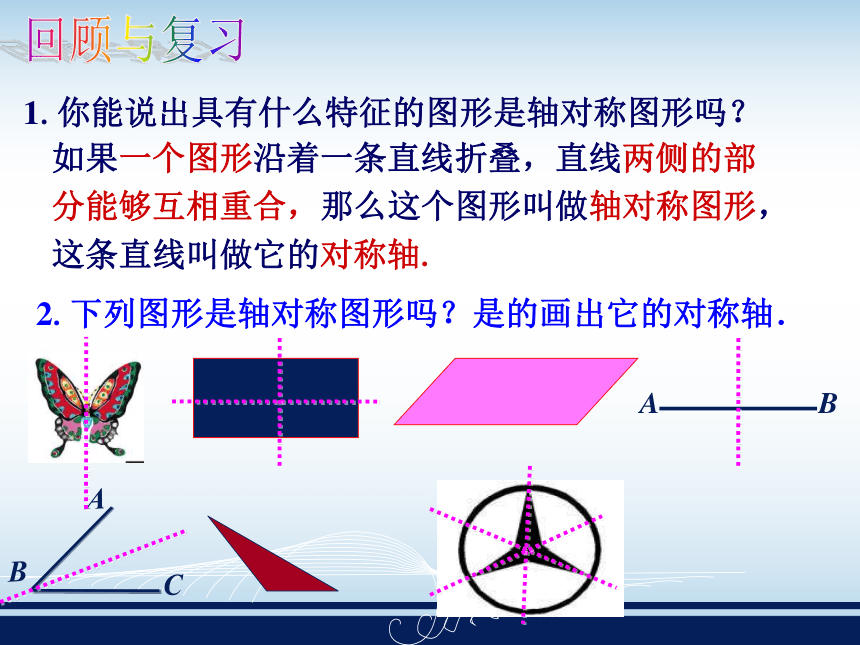
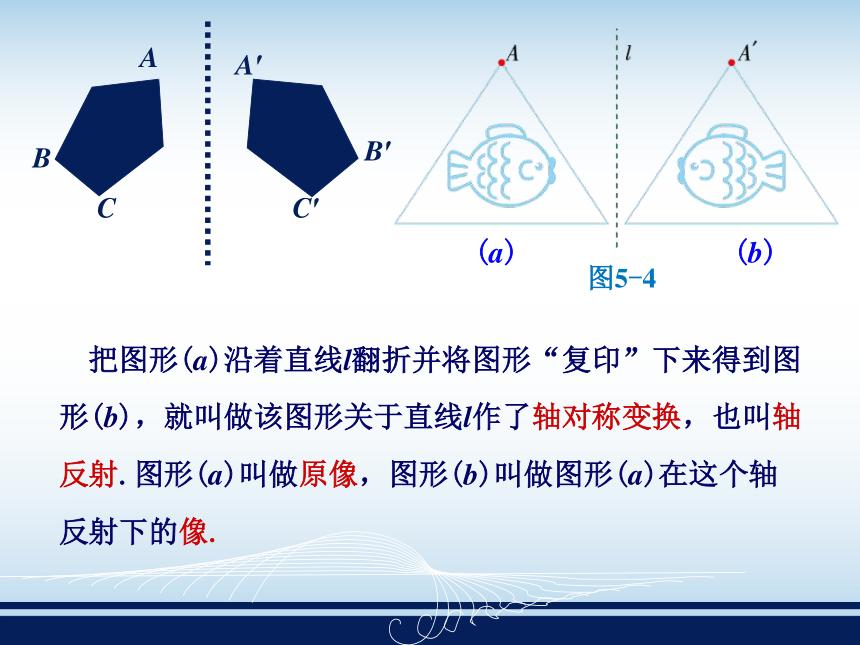
课件17张PPT。回顾与复习1.你能说出具有什么特征的图形是轴对称图形吗？ 如果一个图形沿着一条直线折叠，直线两侧的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线叫做它的对称轴.2.下列图形是轴对称图形吗？是的画出它的对称轴．以水为镜，上面的实物和下面的倒影一样，为什么？图形欣赏轴对称变换 如图，在一张纸上盖上一个印(a)，趁油墨未干之时，将纸张对折得到一个(b)，随后打开，观察图形(a)与(b)会有怎样的现象出现．(a)(b)思考下面每个图案有几个图形？每对图形有什么共同特点？ 把图形(a)沿着直线l翻折并将图形“复印”下来得到图形(b)，就叫做该图形关于直线l作了轴对称变换，也叫轴反射.图形(a)叫做原像，图形(b)叫做图形(a)在这个轴反射下的像. 如果一个图形关于某一条直线做轴对称变换后，能够与另一个图形重合，那么就说这两个图形关于这条直线对称，也称这两个图形成轴对称.这条直线叫做对称轴.原像与像中能互相重合的两个点，其中一点叫做另一个点关于这条直线的对应点. 上图中，对称轴l两边的图形(a)与(b)的形状和大小发生变化了吗？轴对称变换具有下述性质： 轴对称变换不改变图形的形状与大小. 例如：长度、角度和面积等都不改变. 联系：把成轴对称的两个图形看成一个整体，它就是一个轴对称图形； 把一个轴对称图形沿对称轴分成两个图形，这两个图形关于这条直线轴对称. 轴对称与轴对称图形两者之间的联系？相同点：都是关于某一条直线折叠，两部分重合．不同点：轴对称是两个图形．
轴对称图形是一个图形． 在下图 中，三角形 ABC 和三角形A＇B＇C＇关于直线 l 成轴对称，点P和P ＇是对应点，线段PP＇交直线l 于点D. 那么线段 PP＇与对称轴 l 有什么关系呢？ 因为三角形ABC 和三角形A＇B＇C＇关于直线l成轴对称，将图5-5沿直线l折叠，则点P与P＇重合，所以PD与P＇D ，∠1与∠2也互相重合，故有PD=P＇D ，∠1=∠2=90o，因此，l⊥PP＇， 且平分PP＇，即直线 l垂直平分线段 PP ＇.于是，我们就有下面的结论： 从右图 可以看出，如果两个图形的对应点的连线被同一条直线垂直平分，那么这两个图形关于这条直线l对称.如何做一个图形关于一条直线的对称图形？轴对称具有下述性质： 成轴对称的两个图形中，对应点的连线被对称轴垂直平分. 例1 如图 5-6，已知直线 l 及直线外一点P，求作点P＇，使它与点P关于直线l对称.作法： 1. 过点P作 PQ⊥l，交l于点 O.举
例.POP＇lQ图5-62. 在直线 PQ上，截取 OP＇=OP.
则点P＇即为所求作的点. 如图5-7，已知线段AB和直线l，作出与线段AB关于直线l对称的图形.A＇B＇))图5-8作法：1. 过点A作直线l的垂线，垂足为点O，在垂线上截取OA＇= OA，点A＇就是点A关于直线l的对应点.画好三角形 A＇B＇C＇后，若将纸沿直线l对折两个三角形会重合吗？2. 类似地，分别作出点B，C关于直线l的对应点 B＇，C＇.3. 连接A＇B＇，B＇C＇，C＇A＇得到的三角形A＇B＇C＇即为所求.例2 如图5-8，已知三角形ABC和直线l，作出与三角形 ABC关于直线l对称的图形.分析：要作三角形ABC关于直线l的对称图形，只要作出三角形的顶点A，B，C关于直线l的对应点A＇，B＇，C＇，连接这些对应点，得到的三角形A＇B＇C＇就是三角形ABC 关于直线l对称的图形.举
例1. 下列三个图案分别成轴对称吗？如果是，
画出它们的对称轴，并标出一对对应点.2. 图中蓝色的三角形与哪些三角形成轴对称？整个图形是轴对称图形吗？它共有几条对称轴？实践出真知！ 1.以直线l为对称轴，画出ΔABC在轴反射下的像ΔA′B′C′.A′B′C′2.做出五边形ABCDE以直线l为对称轴的对称图形．C′B′A′lD′E′例1 如图所示，将矩形纸片先沿虚线AB按箭头方向向右对折，接着对折后的纸片沿虚线CD向下对折，然后剪下一个小三角形，再将纸片打开，则打开后的展开图是( 　 )
D什么样的图形变换叫轴对称变换(轴反射)？它有哪些性质？ 如何做一个图形关于一条直线对称的图形？说一说轴对称与轴对称图形的关系.区别：轴对称是指的两个图形的位置关系
而轴对称图形是指一个具有特殊状态的图形联系：都是沿着某 一条直线对折，图形 重合．如果把两个成轴对称的图形看成一个整体，那么，它就是一个轴对称图形．反过来把一个轴对称的图形的两 部分当作两 个图形，那么 这两个图形成轴对称