6.1.1 平均数 课件1
图片预览









文档简介
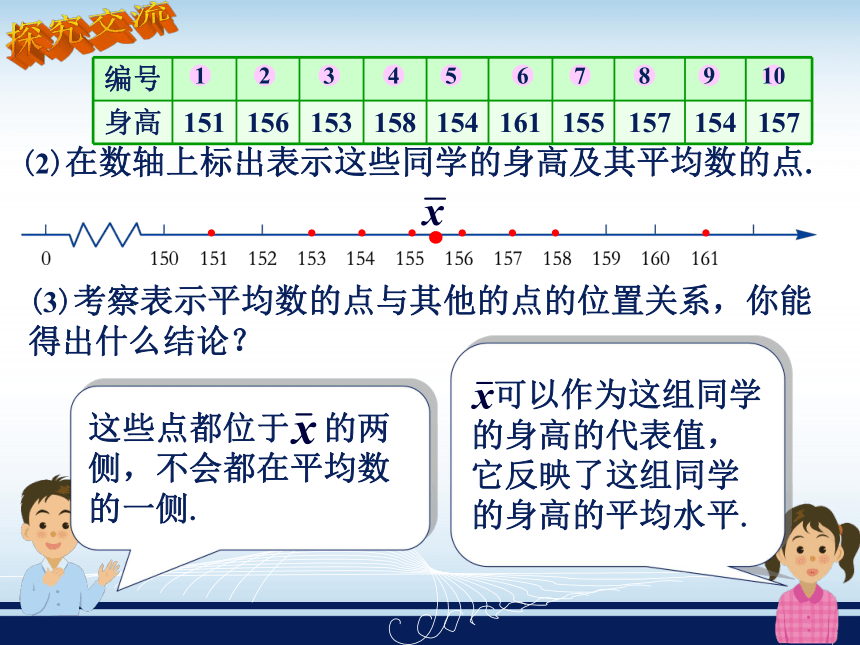
课件30张PPT。小明家种植了100棵梨树即将收获,他想知道总产量大约是多少?小强帮他想了一个方法.你知道小强的方法吗?(1)、任意摘下20个梨子,称出这20个梨子的总重量,再求出这20个梨子的平均重量;(2)从100棵树中任意选出10棵,数出这10棵梨子树上的梨子数,求出这10棵梨子树的平均个数;(3)用“梨子的平均重量×梨子树的平均个数×梨子树的总数”就能得到总产量. 在这个问题中两次用到了平均数,你知道平均数的意义和平均数的优缺点吗?问题情境 在小学我们对平均数有所认识,你能简单的说出平均数的概念吗? 一个小组10名同学的身高(单位:cm)如下表所示:12345678910计算10名同学身高的平均数.平均数=(151+156+153+158+154+161+155+157+154+157)÷10
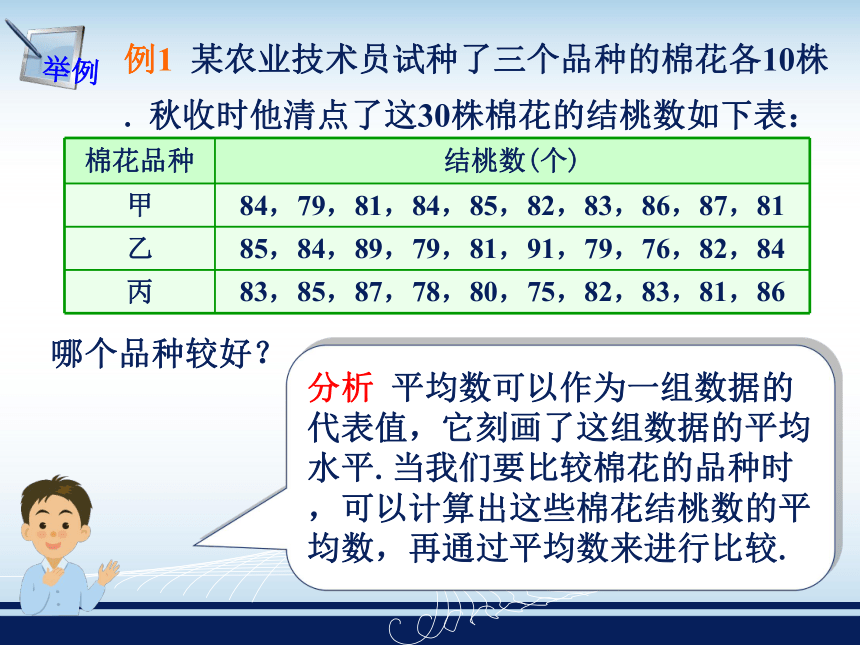
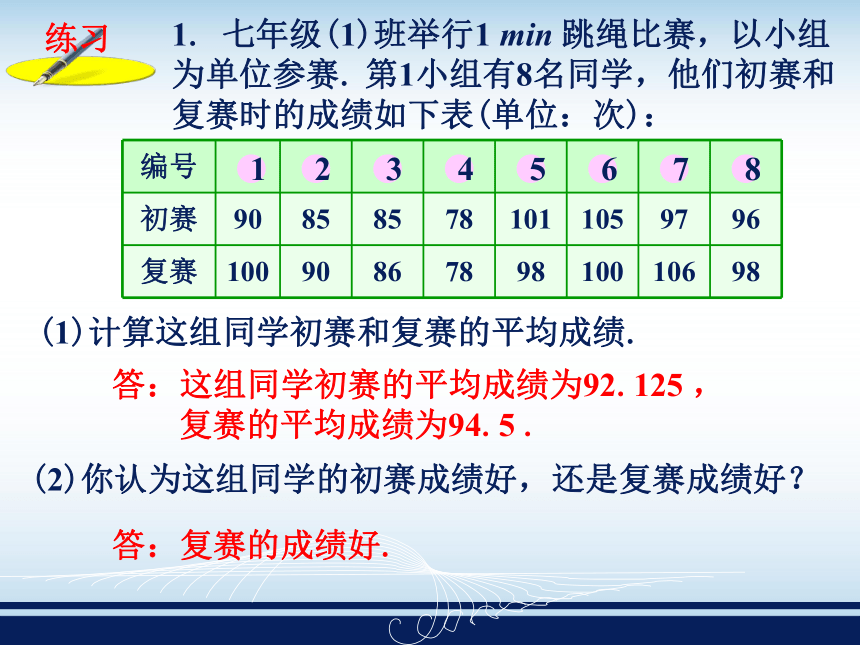
= 155.6(cm).平均数的特征是什么?它怎样刻画一组数据的?新知形成如上面两例为:(2)在数轴上标出表示这些同学的身高及其平均数的点.12345678910探究交流(3)考察表示平均数的点与其他的点的位置关系,你能得出什么结论?这些点都位于 的两侧,不会都在平均数的一侧. 可以作为这组同学的身高的代表值,它反映了这组同学的身高的平均水平.平均数作为一组数据的一个代表值,它刻画了这组数据的平均水平. 平均数的大小与一组数据的每个数据都有关系,如果这组数据中的一个数据变大,其平均数将变大;若这组数据中的一个数据变小,平均数将变小. 2、平均数的作用和特点吗?1、通过上述问题,平均数与数据组的关系是: 平均数是一组数据的数值大小的集中代表值,它刻画了这组数据整体的平均状态,体现了这组数据的整体性质,对于这组数据的个体性质不能作出什么结论.例1 某农业技术员试种了三个品种的棉花各10株. 秋收时他清点了这30株棉花的结桃数如下表:举例哪个品种较好?分析 平均数可以作为一组数据的代表值,它刻画了这组数据的平均水平.当我们要比较棉花的品种时,可以计算出这些棉花结桃数的平均数,再通过平均数来进行比较.则解 设甲、乙、丙三个品种的平均结桃数分别为 由于甲种棉花的平均结桃数高于其他两个品种的平均结桃数,所以我们可以认为甲种棉花较好.个体户张某经营一家餐馆,下面是该餐馆所有工作人员200年10月份的工资: 张某: 4000元;会计: 700元;厨师甲:1000元;乙:900元;杂工甲:580元;乙:560元;服务员甲:620元;乙:600元;丙:580元(1)计算他们的平均工资,这个平均工资能否反映餐馆加工在这个月收入的一般水平?(2)不计张某的工资,再求餐馆员工的月平均工资,这个平均工资能代表一般水平吗?1060元692.5元思考:通过这个问题,说出平均数有什么缺点吗?如何避免这个缺点?平均数容易受个别特殊数据的影响. 为了消除这个缺点,当出现这种情形时,可以将特殊数据去掉.如某些评奖比赛的计分,通常去掉一个最高分和一个最低分.例如:在全校歌咏比赛中,7位评委给一个班级的打分分别是:9.00,8.00,9.10,9.10,9.15,9.00,9.58. 怎样评分比较公正? 但实际上评委的评判受主观因素影响比较大,评分也比较悬殊,为了消除极端数对平均数的影响,一般去掉一个最高分和一个最低分,取最后得分这个分数才比较合理地反映了这个班级的最后得分. 计算器一般有统计功能,我们可以利用该功能求一组数据的平均数. 不同型号的计算器其操作步骤(按键)可能不同,操作时需参阅计算器的说明书. 通常先按统计键,使计算器进入统计运算模式,然后依次输入数据x1 , ,x2, ,…,最后按求平均数的功能键,即可得到该组数据的平均数.创新训练1. 七年级(1)班举行1 min 跳绳比赛,以小组为单位参赛. 第1小组有8名同学,他们初赛和复赛时的成绩如下表(单位:次):12345678(1)计算这组同学初赛和复赛的平均成绩.(2)你认为这组同学的初赛成绩好,还是复赛成绩好?答:这组同学初赛的平均成绩为92.125 ,
复赛的平均成绩为94.5 .答:复赛的成绩好.2. 某跳水队计划招收一批新运动员.请6位评委给选拔赛参加者打分,平均分数超过8.5分才能被选上.刘明在比赛时的成绩为8.30,8.25,8.45,8.20,8.30,9.60,你认为刘明选得上吗?答:刘明的平均分数为8.52,所以刘明能被选上.3. 小明班上同学的平均身高是1.4m,小强班上同学的平均身高是1.45m. 小明一定比小强矮吗?答:不一定.1、某次考试A、B、C、D、E五名学生平均分为62分,除A以外四人平均分为60分,则A得分为( )
A、60 B、62 C、70 D、无法确定C课外练习:2、小明所在班级的男同学的平均体重是45kg,小亮所在班级的男同学的平均体重是42kg,则下列判断正确的是( )A、小明体重是45kgB、小明比小亮重3kgC、小明体重不能确定D、小明与小亮体重相等C3、数据 35,35,35,47,47,84,84,84,84,125.的平均数是 .665、某市的7月下旬最高气温统计如下:该市7月中旬最高气温的平均数是_____.337、小王在学校举行的演讲比赛中,10位评委教师所打的分如下:9.6 , 9.5, 9.2 , 9.0,9.4,9.5 , 9.2, 9.3, 8.4, 9.7你认为怎样计算小王的得分最合理?并求出你认为合理的分数?
6、近年来,我市民用汽车拥有量持续增长,2007年至2011年我市民用汽车拥有量依次约为: 11,13,15,19,x(单位:万辆),这五个数的平均数为16,则x的值为______.22小结1、算术平均数:
一组数据的总和与这组数据的个数之比叫做这组数据的算术平均数.
2、计算公式:对于一组数据x1、x2、x3、…xn平均数是:3、平均数的特征及缺点是什么? 平均数作为一组数据的一个代表值,它刻画了这组数据的平均水平.对于这组数据的个体性质不能作出什么结论.并且容易受个别特殊数据的影响. 问题1:学校举行运动会,入场式中有七年级的一个队列已知这个队列共100人,排成10行,每行10人,其中前两排同学的身高都是160cm,接着的三排同学的身高是155cm,其余五排同学的身高是150cm.求这个队列的同学的平均身高.100名同学的身高有100个数,把它们加起来再除以100,就得到平均数.这组数据中有许多相同的数,相同的数求和可用乘法来计算.平均身高是: 问题2:我想估计七年级数学的平均成绩,抽取每班部分同学的平均分和相应的人数,接下来该怎么办?=160×0.2+155×0.3+150×0.5乙的计算反映了各个数在数据组中所占的比例,它们各是多少?哪一个正确?为什么?两位同学的算法如下:在上面问题1的算式中,0.2,0.3,0.5分别表示160,155,150这三个数在数据组中所占的比例,分别称它们为这三个数的权数.160的权数是0.2,155的权数是0.3,150的权数是0.5, 153.5是160,155,150分别以0.2,0.3,0.5为权的加权平均数.形成概念计算这两个问题中的权数之和,看有什么规律?1. 数据出现的次数的形式.如31,32,28;
2. 比例的形式. 如3:3:2:2;
3. 百分数形式. 如50%,40%,10%.加权平均数权的常见形式 权者,铢、两、斤、钧、石(dan)也,所以称物平施,知轻重也.
——《汉书 · 律历志》 权的意思是,利用铢、两、斤、钧、石,重量不同的秤锤,根据物品的多少,做到施与均衡.这里选取权衡重要程度. 数据的权能反映数据的相对“重要程度”.
权越“大”对平均数的影响就越大.
一般地,权是小于1的非负数,
数据组的权数之和为1.练
习
1.用两种方法计算下列数据的平均数:
35,35,35,47,47,84,84,84,84,125.解 (1)这10个数的平均数是(35+35+35+47+47+84+84+84+84+125)÷10= 66.(2)可求得35,47,84,125的权数分别为0.3,0.2,0.4,0.1,则:所求的加权平均数为:2 一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制, 然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩.如下表所示:35×0.3+47×0.2+84×0.4+125×0.1=66.
例2某纺织厂订购一批棉花,棉花纤维长短不一,主要有3cm,5cm,6cm三种长度. 随意地取出10g棉花并测出三种长度的棉花纤维的含量,得到下面的结果:问:这批棉花纤维的平均长度是多少?分析 在取出的10 g棉花中,长度为3cm,5cm,6cm棉花的纤维各占25%,40%,35%,显然含量多的棉花纤维的长度对平均长度的影响大,所以要用求加权平均数的方法来求出这批棉花纤维的平均长度.解 这批棉花纤维的平均长度是答:这批棉花纤维的平均长度是4.85cm.平均数与加权平均数之间有什么关系? 平均数实质上是加权平均数的一种特殊情况,即各数的权都相等. 平均数都是加权平均数.
而数据的权的差异会影响平均数的大小,所以,加权平均数不一定是平均数,它是平均数的推广.1. 某棒球运动员近50场比赛的得分情况如下表:求该运动员50场比赛得分的平均数.解:
(14×0+26×1+7×2+2×3+1×4)÷50=1.2.某出版社给一本书的作者发稿费,全书20万字,其中正文占总字数的 ,每千字50元;答案部分占总字数的 ,每千字30元.问全书平均每千字多少元?(20× ×50+20× ×30)÷20=463. 商店中有3种糖果,各种糖果的单价如下表所示:商店用水果糖20kg、花生糖30kg、软糖50kg配成什锦糖100kg,问这100kg什锦糖的单价应如何确定?答:
11.6×0.2+14.4×0.3+16×0.5
= 14.64(元).拓展提升 已知数据x1,x2,…,x5的平均数是 ,则一组新数据x1+a,x2+a,…,x5+a的平均数是 ,
a x1,ax2,…,ax5的平均数(2) (ax1+ax2+…ax5)= a(x1+x2+…x5)= a把这个结论推广到n个数据是怎样的 ?加权平均数;
1.算数平均数与加权平均数的关系;
2.权的常见形式.作业:P147 3、4、5、6、7 这节课我们学习了平均数,知道了平均数的计算公式和平均数的作用与特点及平均数的缺点 ,这对我们解决一些与平均数有关的问题将有所帮助.
= 155.6(cm).平均数的特征是什么?它怎样刻画一组数据的?新知形成如上面两例为:(2)在数轴上标出表示这些同学的身高及其平均数的点.12345678910探究交流(3)考察表示平均数的点与其他的点的位置关系,你能得出什么结论?这些点都位于 的两侧,不会都在平均数的一侧. 可以作为这组同学的身高的代表值,它反映了这组同学的身高的平均水平.平均数作为一组数据的一个代表值,它刻画了这组数据的平均水平. 平均数的大小与一组数据的每个数据都有关系,如果这组数据中的一个数据变大,其平均数将变大;若这组数据中的一个数据变小,平均数将变小. 2、平均数的作用和特点吗?1、通过上述问题,平均数与数据组的关系是: 平均数是一组数据的数值大小的集中代表值,它刻画了这组数据整体的平均状态,体现了这组数据的整体性质,对于这组数据的个体性质不能作出什么结论.例1 某农业技术员试种了三个品种的棉花各10株. 秋收时他清点了这30株棉花的结桃数如下表:举例哪个品种较好?分析 平均数可以作为一组数据的代表值,它刻画了这组数据的平均水平.当我们要比较棉花的品种时,可以计算出这些棉花结桃数的平均数,再通过平均数来进行比较.则解 设甲、乙、丙三个品种的平均结桃数分别为 由于甲种棉花的平均结桃数高于其他两个品种的平均结桃数,所以我们可以认为甲种棉花较好.个体户张某经营一家餐馆,下面是该餐馆所有工作人员200年10月份的工资: 张某: 4000元;会计: 700元;厨师甲:1000元;乙:900元;杂工甲:580元;乙:560元;服务员甲:620元;乙:600元;丙:580元(1)计算他们的平均工资,这个平均工资能否反映餐馆加工在这个月收入的一般水平?(2)不计张某的工资,再求餐馆员工的月平均工资,这个平均工资能代表一般水平吗?1060元692.5元思考:通过这个问题,说出平均数有什么缺点吗?如何避免这个缺点?平均数容易受个别特殊数据的影响. 为了消除这个缺点,当出现这种情形时,可以将特殊数据去掉.如某些评奖比赛的计分,通常去掉一个最高分和一个最低分.例如:在全校歌咏比赛中,7位评委给一个班级的打分分别是:9.00,8.00,9.10,9.10,9.15,9.00,9.58. 怎样评分比较公正? 但实际上评委的评判受主观因素影响比较大,评分也比较悬殊,为了消除极端数对平均数的影响,一般去掉一个最高分和一个最低分,取最后得分这个分数才比较合理地反映了这个班级的最后得分. 计算器一般有统计功能,我们可以利用该功能求一组数据的平均数. 不同型号的计算器其操作步骤(按键)可能不同,操作时需参阅计算器的说明书. 通常先按统计键,使计算器进入统计运算模式,然后依次输入数据x1 , ,x2, ,…,最后按求平均数的功能键,即可得到该组数据的平均数.创新训练1. 七年级(1)班举行1 min 跳绳比赛,以小组为单位参赛. 第1小组有8名同学,他们初赛和复赛时的成绩如下表(单位:次):12345678(1)计算这组同学初赛和复赛的平均成绩.(2)你认为这组同学的初赛成绩好,还是复赛成绩好?答:这组同学初赛的平均成绩为92.125 ,
复赛的平均成绩为94.5 .答:复赛的成绩好.2. 某跳水队计划招收一批新运动员.请6位评委给选拔赛参加者打分,平均分数超过8.5分才能被选上.刘明在比赛时的成绩为8.30,8.25,8.45,8.20,8.30,9.60,你认为刘明选得上吗?答:刘明的平均分数为8.52,所以刘明能被选上.3. 小明班上同学的平均身高是1.4m,小强班上同学的平均身高是1.45m. 小明一定比小强矮吗?答:不一定.1、某次考试A、B、C、D、E五名学生平均分为62分,除A以外四人平均分为60分,则A得分为( )
A、60 B、62 C、70 D、无法确定C课外练习:2、小明所在班级的男同学的平均体重是45kg,小亮所在班级的男同学的平均体重是42kg,则下列判断正确的是( )A、小明体重是45kgB、小明比小亮重3kgC、小明体重不能确定D、小明与小亮体重相等C3、数据 35,35,35,47,47,84,84,84,84,125.的平均数是 .665、某市的7月下旬最高气温统计如下:该市7月中旬最高气温的平均数是_____.337、小王在学校举行的演讲比赛中,10位评委教师所打的分如下:9.6 , 9.5, 9.2 , 9.0,9.4,9.5 , 9.2, 9.3, 8.4, 9.7你认为怎样计算小王的得分最合理?并求出你认为合理的分数?
6、近年来,我市民用汽车拥有量持续增长,2007年至2011年我市民用汽车拥有量依次约为: 11,13,15,19,x(单位:万辆),这五个数的平均数为16,则x的值为______.22小结1、算术平均数:
一组数据的总和与这组数据的个数之比叫做这组数据的算术平均数.
2、计算公式:对于一组数据x1、x2、x3、…xn平均数是:3、平均数的特征及缺点是什么? 平均数作为一组数据的一个代表值,它刻画了这组数据的平均水平.对于这组数据的个体性质不能作出什么结论.并且容易受个别特殊数据的影响. 问题1:学校举行运动会,入场式中有七年级的一个队列已知这个队列共100人,排成10行,每行10人,其中前两排同学的身高都是160cm,接着的三排同学的身高是155cm,其余五排同学的身高是150cm.求这个队列的同学的平均身高.100名同学的身高有100个数,把它们加起来再除以100,就得到平均数.这组数据中有许多相同的数,相同的数求和可用乘法来计算.平均身高是: 问题2:我想估计七年级数学的平均成绩,抽取每班部分同学的平均分和相应的人数,接下来该怎么办?=160×0.2+155×0.3+150×0.5乙的计算反映了各个数在数据组中所占的比例,它们各是多少?哪一个正确?为什么?两位同学的算法如下:在上面问题1的算式中,0.2,0.3,0.5分别表示160,155,150这三个数在数据组中所占的比例,分别称它们为这三个数的权数.160的权数是0.2,155的权数是0.3,150的权数是0.5, 153.5是160,155,150分别以0.2,0.3,0.5为权的加权平均数.形成概念计算这两个问题中的权数之和,看有什么规律?1. 数据出现的次数的形式.如31,32,28;
2. 比例的形式. 如3:3:2:2;
3. 百分数形式. 如50%,40%,10%.加权平均数权的常见形式 权者,铢、两、斤、钧、石(dan)也,所以称物平施,知轻重也.
——《汉书 · 律历志》 权的意思是,利用铢、两、斤、钧、石,重量不同的秤锤,根据物品的多少,做到施与均衡.这里选取权衡重要程度. 数据的权能反映数据的相对“重要程度”.
权越“大”对平均数的影响就越大.
一般地,权是小于1的非负数,
数据组的权数之和为1.练
习
1.用两种方法计算下列数据的平均数:
35,35,35,47,47,84,84,84,84,125.解 (1)这10个数的平均数是(35+35+35+47+47+84+84+84+84+125)÷10= 66.(2)可求得35,47,84,125的权数分别为0.3,0.2,0.4,0.1,则:所求的加权平均数为:2 一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制, 然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩.如下表所示:35×0.3+47×0.2+84×0.4+125×0.1=66.
例2某纺织厂订购一批棉花,棉花纤维长短不一,主要有3cm,5cm,6cm三种长度. 随意地取出10g棉花并测出三种长度的棉花纤维的含量,得到下面的结果:问:这批棉花纤维的平均长度是多少?分析 在取出的10 g棉花中,长度为3cm,5cm,6cm棉花的纤维各占25%,40%,35%,显然含量多的棉花纤维的长度对平均长度的影响大,所以要用求加权平均数的方法来求出这批棉花纤维的平均长度.解 这批棉花纤维的平均长度是答:这批棉花纤维的平均长度是4.85cm.平均数与加权平均数之间有什么关系? 平均数实质上是加权平均数的一种特殊情况,即各数的权都相等. 平均数都是加权平均数.
而数据的权的差异会影响平均数的大小,所以,加权平均数不一定是平均数,它是平均数的推广.1. 某棒球运动员近50场比赛的得分情况如下表:求该运动员50场比赛得分的平均数.解:
(14×0+26×1+7×2+2×3+1×4)÷50=1.2.某出版社给一本书的作者发稿费,全书20万字,其中正文占总字数的 ,每千字50元;答案部分占总字数的 ,每千字30元.问全书平均每千字多少元?(20× ×50+20× ×30)÷20=463. 商店中有3种糖果,各种糖果的单价如下表所示:商店用水果糖20kg、花生糖30kg、软糖50kg配成什锦糖100kg,问这100kg什锦糖的单价应如何确定?答:
11.6×0.2+14.4×0.3+16×0.5
= 14.64(元).拓展提升 已知数据x1,x2,…,x5的平均数是 ,则一组新数据x1+a,x2+a,…,x5+a的平均数是 ,
a x1,ax2,…,ax5的平均数(2) (ax1+ax2+…ax5)= a(x1+x2+…x5)= a把这个结论推广到n个数据是怎样的 ?加权平均数;
1.算数平均数与加权平均数的关系;
2.权的常见形式.作业:P147 3、4、5、6、7 这节课我们学习了平均数,知道了平均数的计算公式和平均数的作用与特点及平均数的缺点 ,这对我们解决一些与平均数有关的问题将有所帮助.
